Яковлев В.В. Экологическая безопасность, оценка риска

Подождите немного. Документ загружается.

251

3,2

⋅

−

−=

BAy

(12.1.48)

где

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

=−−=+−=

(12.1.49)

Подстановкой найденных корней (12.1.48) в (12.1.46) и последую-

щим решением (12.1.43) получим искомую функцию изменения радиуса

растекания нефтяного пятна на втором этапе методики Fay.

Замечание.

Если кубическое уравнение (12.1.47) действительно, то оно имеет

или один действительный корень и два сопряженных комплексных корня,

или три действительных корня, по крайней мере два из которых равны,

или три различных действительных корня в зависимости от того, будет

ли Q соответственно положительно, равно нулю или отрицательно.

Решения (12.1.38)…(12.1.48) положены в основу программы ISP-F, с

помощью которой проведены расчеты, представленные в табл. 12.1.10.

В экспериментах установлено, что наибольшая часть нефти испаря-

ется в первые 30 мин. В дальнейшем скорость испарения постоянно замед-

ляется и через 3…4 часа после разлива процесс испарения практически

прекращается. К этому времени может испариться до 30% начального объ-

ема легкой нефти.

Таблица 12.1.10.

Массовая скорость

испарения и давление насыщенных паров неко-

торых нефтепродуктов.

Нефтепродукт Плотность,

кг/м

Массовая ско-

рость испарения,

кг/м

⋅с

Давление

насыщенных паров при

температуре 20°С,

кПа

Бензин Б-70 750

79.0⋅10

- 6

10.92

Бензин А-72 750

280⋅10

- 6

39.54

Бензин АИ-93 750

179⋅10

- 6

25.56

Дизельное топливо 820

0.67⋅10

- 6

0.065

Керосин 800

2.12⋅10

- 6

0.238

Бензол 800

63.5⋅10

- 6

9.98

252

12.2. Аварийное истечение вязких жидкостей из резервуаров раз-

личной формы.

Все нефтепродукты, в том числе и нефть, относятся к категории вяз-

ких жидкостей. В случае возникновения частичной разгерметизации резер-

вуаров хранения или транспортировки нефтепродуктов, их истечение через

аварийное отверстие (пробоину) происходит постепенно и рассчитывается

достаточно сложно. Истечение может происходить как на

водную поверх-

ность, так и на твердые подстилающие поверхности (грунт, асфальт, бе-

тон).

Возникает необходимость решения следующих задач:

- расчет времени полного истечения жидкости из емкости через

аварийное отверстие;

- расчет параметров процесса растекания нефтепродуктов по

твердым подстилающим поверхностям в помещениях и в ре-

альных метеоусловиях;

- определение изменения массы

испарившегося нефтепродукта

за определенное время истечения.

Оценка времени аварийного истечения нефтепродуктов из емко-

стей различной формы.

В общем случае, как известно из основ гидродинамики [39], время

понижения уровня жидкости в сосуде произвольного профиля от значения

высоты над аварийным отверстием Н

до значения Н

определяется урав-

нением:

∫

⋅⋅⋅⋅−

)(

hgsQ

dhhf

(12.2.1)

где f(h) - функция изменения площади свободной поверхности ре-

зервуара с высотой;

h - текущее значение высоты зеркала жидкости над центром

аварийного отверстия;

Q - приток жидкости в резервуар;

µ - коэффициент расхода или коэффициент сопротивления ис-

течению нефтепродукта;

s - площадь отверстия или пробоины, приведенная к кругово-

му сечению.

Резервуары с постоянным сечением.

253

Если внешний приток отсутствует, (Q = 0) и профиль сосуда не из-

меняется с высотой f(h)=const=F, время изменения уровня жидкости от

уровня H

до уровня H

из решения (12.2.1) определится зависимостью:

()

t −

⋅⋅⋅

⋅

(12.2.2)

При H

= 0, т.е. при определении времени полного истечения жидко-

сти из резервуара (от начальной высоты Н

зеркала нефтепродукта над

пробоиной до середины сечения аварийного отверстия), выражение

(12.2.2) принимает вид:

Hgs

⋅⋅⋅⋅

⋅⋅

⋅⋅⋅

⋅⋅

µµ

(12.2.3)

где Н

– начальное значение расстояния по вертикали от поверхности

жидкости до середины сечения пробоины;

F - площадь зеркала жидкости (площадь резервуара).

Значения коэффициентов сопротивления истечению нефтепродуктов

µ в зависимости от кинематической вязкости жидкости при истечении че-

рез круглое (или приведенное к круговому сечению) отверстие представ-

лены в табл. 12.2.1, [40].

Таблица 12.2.1.

Зависимость значений коэффициента сопротивления

истечению µ

от вязкости жидкости.

Кинематический

коэффициент

вязкости ,

Ст

0.01-0.1 0.2 0.4 0.6 0.8 1.0 2.0

Коэффициент

расхода

0.61 0.51 0.41 0.36 0.33 0.3 0.26

Напомним соотношения:

Стокс: 1 Ст = 10

-4

/с; сантистокс: 1 сСт = 10

-6

/с.

При выполнении прогнозных или оценочных расчетов можно вос-

пользоваться аппроксимацией:

6153.01032.51077.1

327

+⋅⋅−⋅⋅=

ννµ

(12.2.4)

где ν - коэффициент кинематической вязкости жидкости, м

/с.

Пример 12.2.1.

Резервуар РВС-5000, имеющий форму вертикального цилиндра диа-

метром 20.92 м, высотой 14.9 м, полностью заполнен нефтью.

Плотность нефти 850 кг/м

, кинематический коэффициент вязкости

52⋅10

-6

/с.

На расстоянии 1.5 м от дна резервуара образовалось аварийное от-

верстие круглого сечения диаметром 25 см.

254

Определить массу утечки нефти за время ликвидации неисправности,

равное 30 мин.

Решение.

1. Высота зеркала нефти над отверстием Н

= 14.9 - 1.5 = 13.4 м.

2. По формуле (12.2.4) находим коэффициент сопротивления исте-

чению нефти через пробоину:

()

386.06153.010521032.510521077.1

=+⋅⋅⋅−⋅⋅⋅=

−−

3. Из уравнения (12.2.2) находим выражение для высоты зеркала

нефти над отверстием в момент t окончания истечения:

⎥

⎦

⎤

⎢

⎣

⎡

−=

где:

⋅⋅⋅

⋅

RF ⋅=

R - радиус резервуара, м.

Подставив числовые значения, получим:

()

мH 74.7878.066.3

9.2048

1800

04.13

=−=

⎟

⎠

⎞

⎜

⎝

⎛

−=

4. Разность высот зеркала в процессе истечения нефти

66.574.74.13

−

=−=∆ ННН

5. Объем нефти, истекшей из резервуара за время 30 мин:

1944

92.20

14.366.5

HFHV =

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅=

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅∆=⋅∆=

6. Масса m вылитой нефти равна:

106524.18501944 ⋅=⋅=⋅=

кг

Таким образом, из общей массы М нефти, содержавшейся в ре-

зервуаре:

1035.485055.3439.14

⋅=⋅⋅=⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅=⋅=

ρπρ

HVM

кг

вытечет 1.6524⋅10

кг, что составит 37.9% от первоначальной массы

нефти в резервуаре.

Резервуары сферической формы.

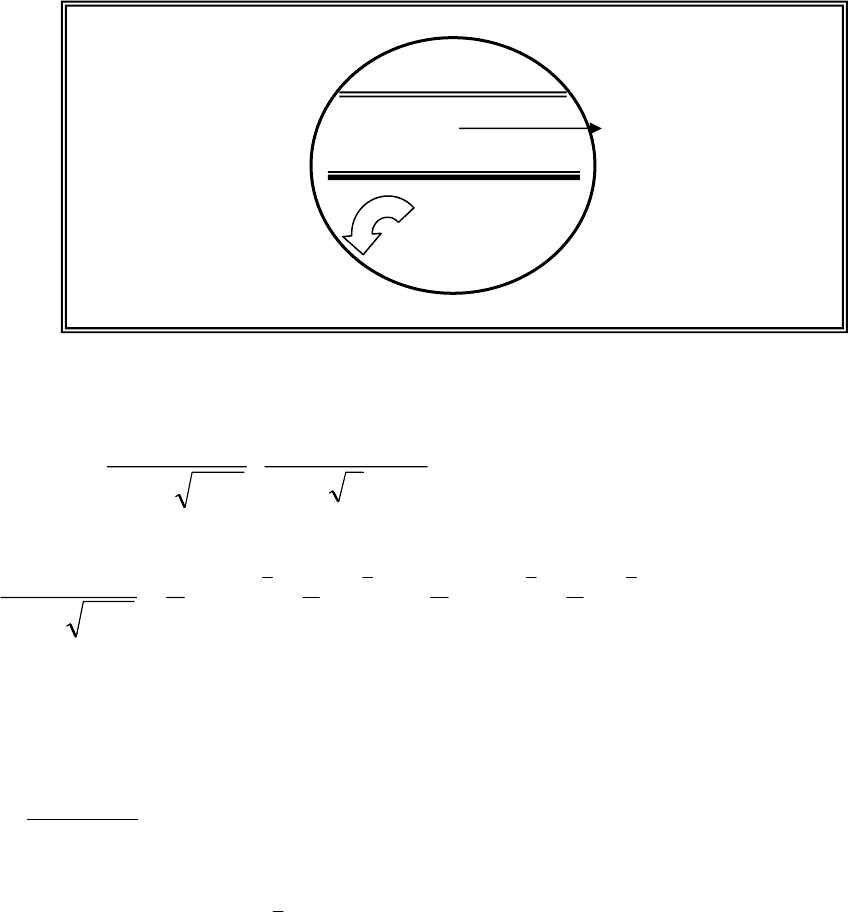
Для резервуаров сферической формы, характерной для стационар-

ных парков хранения нефтепродуктов, зависимость площади зеркала жид-

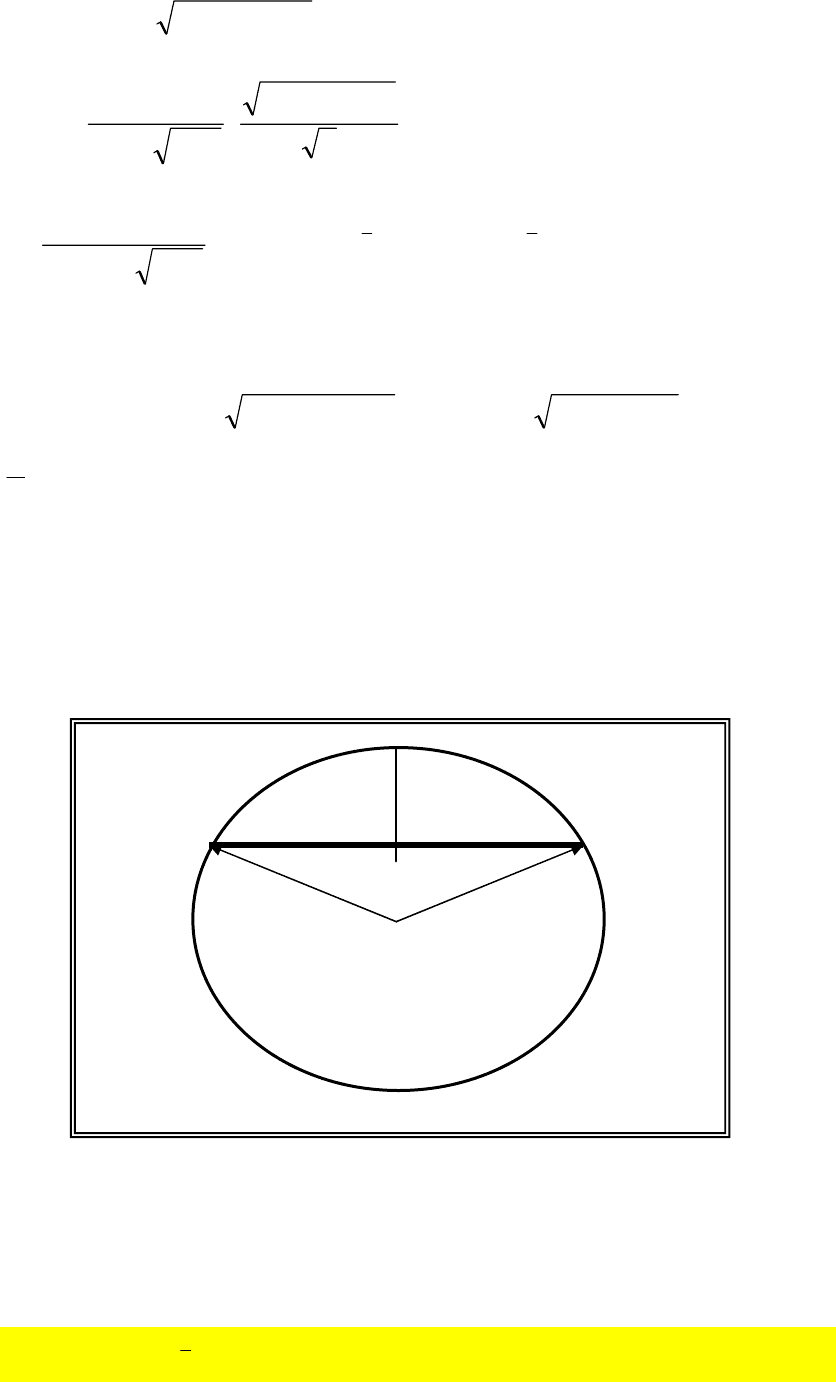
кости от высоты сливного отверстия имеет вид (рис.12.2.1):

255

(

)

2)( hhRhf −⋅⋅⋅=

(12.2.5)

Начальный уровень H

Конечный уровень H

Рис. 12.2.1. Пояснение к выводу зависимости времени истечения

нефтепродуктов из сферического резервуара.

Подставив (12.2.5) в выражение (12.2.1), получим при отсутствии

внешнего притока (Q=0):

hRh

∫

−⋅⋅

⋅

⋅⋅⋅

−=

)2(

(12.2.6)

После интегрирования имеем:

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

⋅−⋅⋅−

⎟

⎠

⎞

⎜

⎝

⎛

⋅−⋅⋅

⋅⋅⋅

⋅

HHRHHR

(12.2.7)

Пример 12.2.2.

За какое время нефть, заполняющая полусферический котел диамет-

ром D=2⋅R

=2 м, вытечет из него через круглое отверстие на дне радиусом

мr

1.0=

Решение.

Изменение радиуса зеркала нефти в зависимости от высоты отвер-

стия истечения определяется выражением:

()

2)( hhRhr −⋅⋅=

где h – текущее значение высоты отверстия от верхнего уровня жид-

кости.

Для резервуара шарообразной формы площадь зеркала жидкости F

определяется зависимостью:

(

)

2)( hhRhrF −⋅⋅⋅=⋅=

ππ

Уравнение истечения нефти из отверстия на дне рассматриваемого

резервуара может быть выведено на основании равенства объемов жидко-

сти в резервуаре, уменьшенной за время dt на высоту dh и объема вытек-

шей жидкости за то же малое время dt:

(

)

dtwhrdhRhh ⋅⋅⋅=⋅⋅⋅−⋅ )(2

ππ

Истечение

нефтепродукта

256

Время t истечения нефти из резервуара шарообразной формы от на-

чального уровня H

(при t=0) до уровня

(по окончании процесса истече-

ния) определится выражением:

()

∫

⋅⋅⋅⋅−

−⋅⋅⋅

hgsQ

hhR

При отсутствии стороннего притока нефти в резервуар, т.е. при Q=0,

после преобразований и интегрирования получим формулу:

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

⋅−⋅⋅−

⎟

⎠

⎞

⎜

⎝

⎛

⋅−⋅⋅

⋅⋅⋅

⋅

HHRHHR

Принимая кинематический коэффициент вязкости нефти равным

υ = 52 сСт = 52⋅10

-6

/с

По формуле (12.2.4) получим значение коэффициента сопротивления

истечению:

()

386.06153.010521032.510521077.1

=+⋅⋅⋅−⋅⋅⋅=

−−

Тогда искомое значение времени максимального истечения нефти из

котла будет равно при Н

=1 м, Н

=0, R

=1 м:

сt 551

167.0

43.401.014.3386.0

14.32

≈

⎥

⎦

⎤

⎢

⎣

⎡

⋅−⋅⋅

⋅⋅⋅

⋅

≈

Решение той же задачи при истечении воды (µ = 0.6) даст результат

t ≈ 35 c.

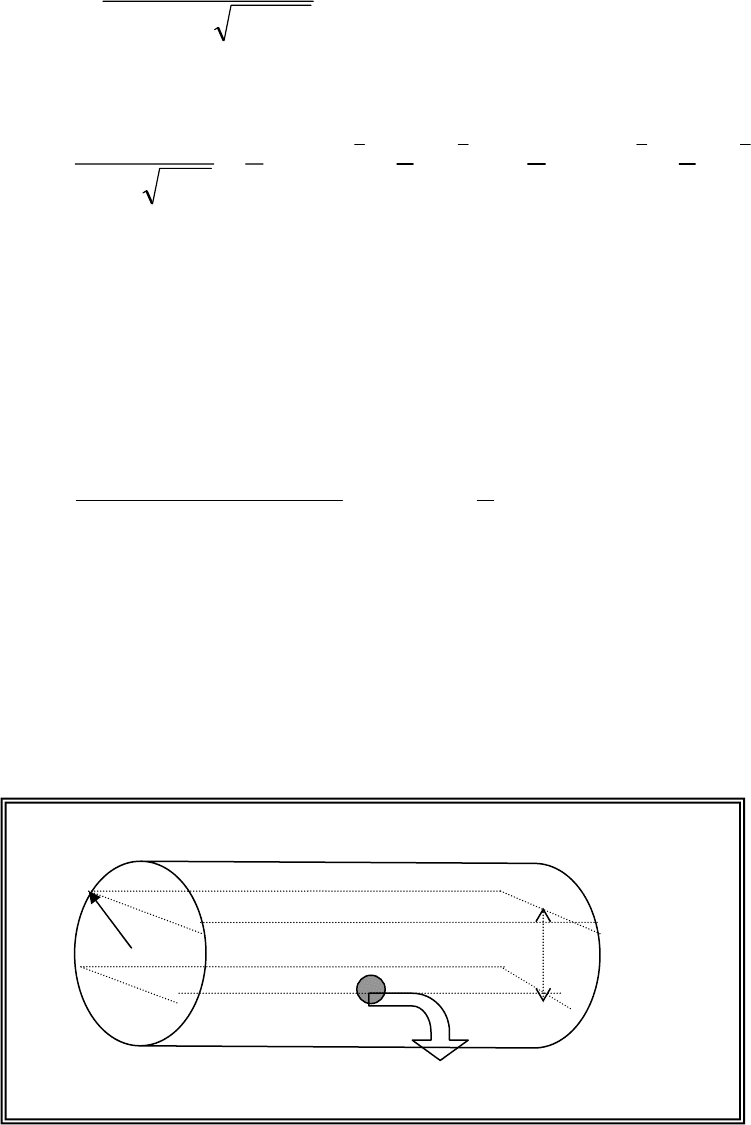
Резервуары в виде круглого горизонтального цилиндра.

Рис. 12.2.2. Истечение нефтепродукта из круглого цилиндра.

Для горизонтальных резервуаров цилиндрической формы, характер-

ной для железнодорожных цистерн, зависимость площади зеркала жидко-

сти от высоты уровня

h имеет вид (рис. 12.2.2):

257

22)( hRhLhf −⋅⋅⋅⋅=

(12.2.8)

Подставив (12.2.8) в выражение (12.2.1), получим при Q=0:

∫

−⋅⋅

⋅

⋅⋅⋅

⋅

−=

hhR

(12.2.9)

После интегрирования и незначительных преобразований имеем:

()()

⎥

⎦

⎤

⎢

⎣

⎡

−⋅−−⋅⋅

⋅⋅⋅⋅

⋅

HRHR

(12.2.10)

Вывод зависимости вытекшей жидкости из горизонтального кругло-

го цилиндра от времени истечения.

Площадь обозначенного на рис. 12.2.3 сегмента равна:

()

[

]

225852359.0)( hhrhrhhrrhS −⋅⋅⋅−⋅−⋅+⋅⋅⋅⋅≈

(12.2.11)

Тогда, при отсчете h от дна цилиндра оставшийся объем будет равен:

)()( hSLhV ⋅=

(12.2.12)

где L – длина образующей цилиндра.

Соответственно, вытекший объем составит:

))()(()(

HSHSLhV −⋅=

(12.2.13)

где Н

, Н

– исходное и конечное значение высоты уровня нефтепро-

дукта от дна цилиндра.

r r

Рис. 12.2.3. Торцевая стенка цилиндра в виде круга радиусом r, высо-

той h, длиной секущей, равной а.

Если известна функция h(t) изменения высоты уровня жидкости со

временем, то будет легко получена зависимость V(t) изменения

во времени

объема (при известной плотности – и масса) вытекающей из цилиндра

жидкости.

Для горизонтального круглого цилиндра после интегрирования

(12.2.9), имеем:

()

2 hrKt −⋅⋅=

(12.2.14)

258

где

[]

, HHh ∈

⋅⋅⋅

⋅=

µ - коэффициент сопротивления истечению вязкой жидкости,

– площадь аварийного отверстия, приведенного к круговой

форме.

После возведения левой и правой части уравнения (12.2.14) в степень

2/3 и разрешения относительно h, получим:

2)(

⎟

⎠

⎞

⎜

⎝

⎛

−⋅=

rth

(12.2.15)

Подставив выражение (12.2.15) в (12.2.11) , получим зависимость

площади сегмента от времени истечения нефтепродукта, используя далее

выражение (12.2.13), получим зависимость объема вытекающей жидкости

от времени истечения.

Пример 12.2.3.

Железнодорожная цистерна имеет форму, близкую к форме круглого

горизонтального цилиндра. Длина цистерны 10 м, диаметр 3 м. Цистерна

полностью заполнена нефтью (плотность ρ=850 кг/м

, коэффициент кине-

матической вязкости υ=52⋅10

-6

/с). На высоте 0.5 м от дна цистерны об-

разовалось круглое отверстие диаметром 4 см (радиусом 0.02 м).

Требуется определить:

- время полного истечения нефти из цистерны,

- изменение объема и массы вытекающей нефти по мере истечения.

Решение.

Алгоритм решения сводится к следующему.

1. Вычисление коэффициента сопротивления истечению µ=µ(υ).

2. Вычисление площади аварийного отверстия.

3. Вычисление полного объема цистерны.

4. Вычисление исходного объема (массы) нефти в цистерне по за-

данным значениям исходной высоты нефти Н

и высоты отвер-

стия Н

5. Определение максимального времени истечения нефти из цистер-

ны через аварийное отверстие.

6. Задание шага изменения времени истечения (от 0 до максималь-

ного значения).

7. Расчет для каждого значения времени высоты сегмента h(t).

8. Расчет площади S(h(t)) сегмента по формуле (12.2.11).

9. Вычисление вытекшего объема V(t) по формуле:

[]

))(()()(

thSHSLtV −⋅=

В результате решения, выполненного по программе “OBCIL-1” по

приведенному выше алгоритму, получено:

259

- время полного истечения нефти из цистерны (до уровня, равного

высоте аварийного отверстия) составляет 24509 сек;

- полный объем нефти в цистерне равен 70.65 м

(60005 кг);

- объем нефти над аварийным отверстием равен 61.2 м

(52032 кг);

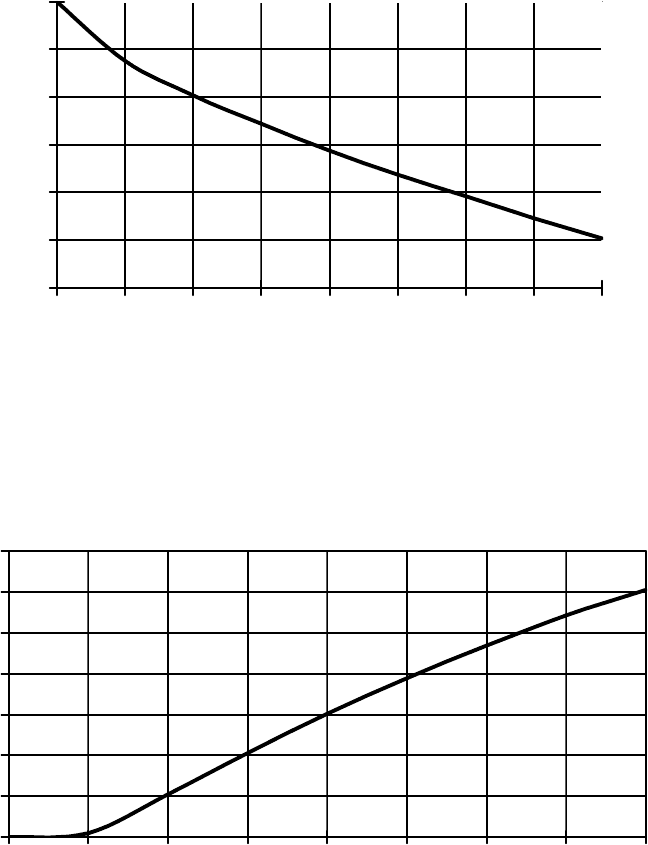
Изменение высоты уровня нефти в цистерне, вытекшего объема и

массы нефти по мере истечения представлены на рисунках 12.2.4, 12.2.5,

12.2.6.

0,5

1,5

2,5

0 50 100 150 200 250 300 350 400

Время истечения, мин

Высота уровня нефти, м

Рис. 12.2.4. Изменение высоты уровня нефти от дна цистерны

во времени.

0 50 100 150 200 250 300 350 400

Время истечения, мин

Вытекший объем, куб.м

Рис. 12.2.5. Изменение объема вытекающей нефти.

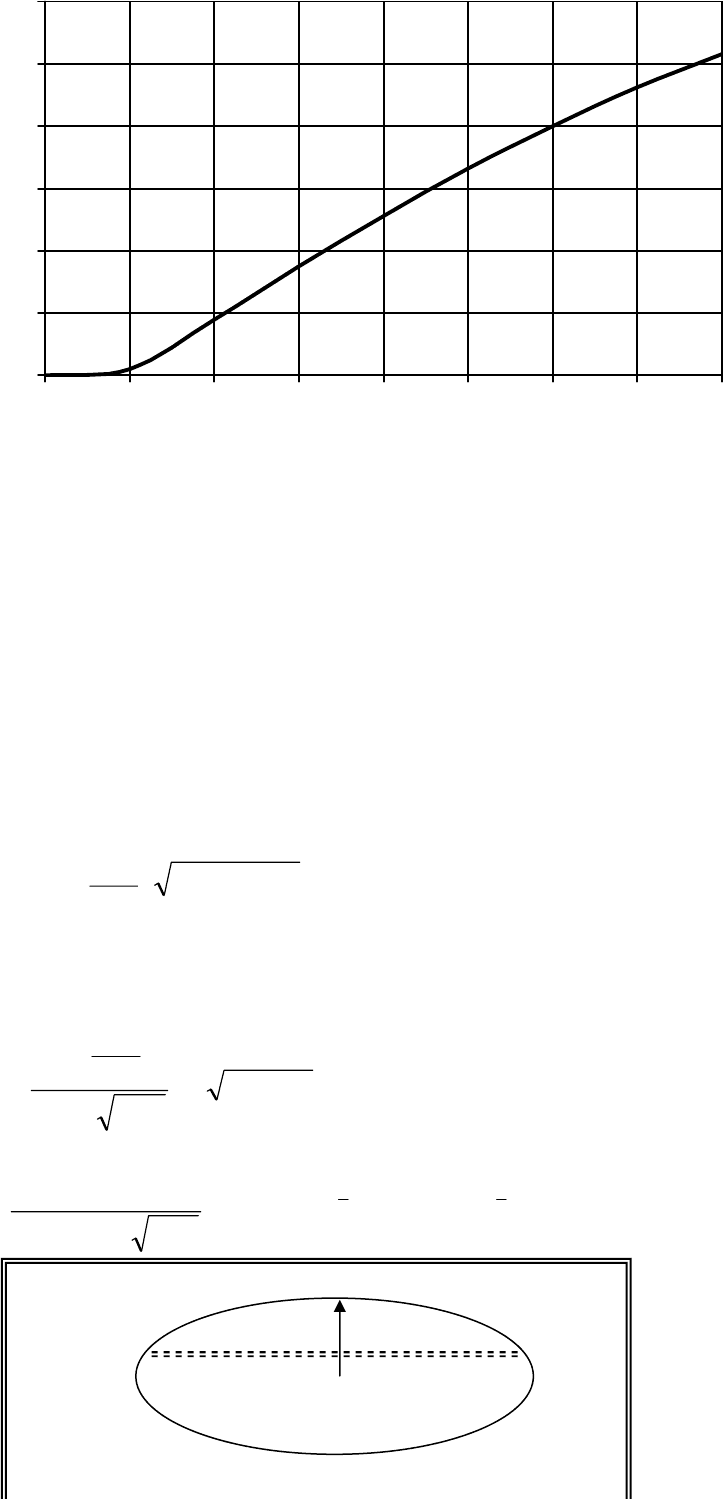
260

0 50 100 150 200 250 300 350 400

Время истечения нефти, мин

Масса вытекшей нефти, т

Рис. 12.2.6. Изменение массы вытекающей нефти по мере ис-

течения.

Применяя далее методику расчета радиуса растекания нефтепродук-

тов по соответствующей твердой подстилающей поверхности, можно оп-

ределить объем облака паровоздушной смеси, и при ее воспламенении –

параметры воздушной ударной волны (при взрывном горении) или пара-

метры теплового потока (при пожаре разлития).

Эллиптические горизонтальные

цилиндры.

Для резервуаров эллиптической формы (рис. 12.2.7), характерной для

автомобильных цистерн, зависимость площади f(h) зеркала жидкости от

высоты уровня при длине цистерны L имеет вид:

)( hhb

Lhf −⋅⋅⋅

⋅

⋅=

(12.2.16)

где h - текущая координата высоты жидкости.

После подстановки функции (12.2.16) в уравнение (12.2.1), получим

при Q=0:

dhhb

∫

−⋅⋅

⋅⋅⋅

⋅

−=

(12.2.17)

После интегрирования имеем:

()()

⎥

⎦

⎤

⎢

⎣

⎡

−⋅−−⋅

⋅⋅⋅⋅⋅

⋅⋅

HbHb

gsb

(12.2.18)

Уровень H