Яковлев А.В. Надежность информационных систем
Подождите немного. Документ загружается.


21
представление о случайной величине дает закон распределения случайной вели-
чины – соотношение между значениями случайной величины и их вероятностями.
Экспоненциальный закон. Функция распределения случайной величины:
)(1)( tQetF
t
=−=
−
λ
(2.2)
где
λ - интенсивность (среднее число событий в единицу времени) появления
случайного события. Далее под t будем подразумевать время до возникновения
отказа.
Функция плотности распределения времени до отказа:
[]
t
e
dt
tdP
tP
dt
d
tF
dt
d
tf
λ
λ
−
=−=−==
)(
)(1)()(
(2.3)
где
t
etP
λ
−
=
)(
(2.4)
это вероятность того, что за время
t отказ не возникнет.
Интенсивность отказов
)(
t
λ
изменяется во времени следующим образом:
const
e
e
tP
tf
t
t
t
====
−
−
λ
λ
λ
λ
λ
)(
)(
)(
(2.5)
Таким образом, признаком экспоненциального закона распределения време-
ни до отказа служит постоянство интенсивности отказов, что характерно для вне-
запных отказов на интервале времени, когда период приработки аппаратуры за-
кончился, а период износа и старения еще не начался. Также постоянной стано-
вится
λ
системы, если отказы вызываются отказами большого числа комплек-
тующих элементов, отказ каждого из которых приводит к отказу объекта.
Этими факторами, а также тем, что экспоненциальное распределение слу-
чайной величины существенно упрощает расчеты надежности, не вызывая значи-
тельных погрешностей, обусловлено широкое применение экспоненциального за-
кона в инженерной практике.
В табл. 2.1 приведены значения интенсивностей отказов для некоторых рас-
пространенных элементов ИС.
Таблица 2.1
Элементы и устройства
λ⋅10
-6
1/ч
Интегральная схема
Диод
Транзистор
Конденсатор
Резистор
Трансформатор
Разъем
Триггер на интегральных схемах
Память на дисках
Контроллер
Специализированная ЭВМ (13000 интегральных схем)
0,1
0,2 – 0,5
0,05 –0,3
0,002 – 0,04
0,01 –0,1
0,1 – 0,2
2 – 3,5
0,1
250
10 – 15
40
22
Закон Пуассона. Вероятность того, что на интервале времени
t
произойдет
n
случайных событий (отказов) определяется формулой:
(3.6) ,
!
)(
a
n
n
e
n
a
tP
−
=
где
ta
λ=
- среднее число отказов на интервале времени
t
.
Время между двумя соседними событиями (отказами) подчиняется экспо-
ненциальному распределению с параметром
λ , т.е. вероятность того, что на уча-
стке времени
τ
, следующим за одним из отказов, не появится ни одного отказа,
равна:
.)(
λτ−
=
etP
Пример 3.1. Определить вероятность того, что за время
100=t ч произой-
дет 0-2 отказа, если
025,0
=λ
.
Решение
1) Среднее число отказов за время
t
:
5,2
== ta λ
.
2) Вероятность отсутствия отказов
.082,0)100(
5,2
0
==
−
eP
3) Вероятность одного отказа:
205,0
1
)5,2(
)100(
5,2
1
1
==
−
eP
.
4) Вероятность двух отказов: .256,0
2
)5,2(
)100(
5,2
2
2
==
−
eP
Распределение Вейбулла. Модель распределения случайной величины, пред-
ложенная шведским ученым Вейбуллом, находит широкое применение ввиду сво-
ей простоты и гибкости, так как в зависимости от значений параметров, характер
модели видоизменяется. Она удобна для выбора наиболее подходящего аналити-
ческого выражения для определения показателей надежности объекта на основе
опытных данных.
Вероятность безотказной работы за время t:
(3.7) ,)(
0
α
λ
t
etP
−
=
где αλ ,
0
- параметры закона распределения.
Функция плотности распределения времени до отказа:
(3.8) .
)(
)(
0
1
0
α
λ
α
αλ
t
et
dt
tdP
tf
−
−
⋅⋅=−=
Интенсивность отказов:
(3.9)
)(
)(
)(
.
1
0
−
⋅==
α
αλλ
t
tP
tf
t
Если
1
=α
, то распределение Вейбулла совпадает с экспоненциальным рас-
пределением, у которого
0
λλ=
. Если
1
<α
, интенсивность отказов - монотонно
убывающая функция; при
1>α
интенсивность отказов - монотонно возрастающая
функция (рис. 3.1).

23
λ
(
t
)
t
α
=1
α
<1
α
>1
Рис 3.1 Зависимость
λ
=f(t) в модели
надежности Вейбулла
Ориентировочно значение
4,02,0 ÷=α
для электронных устройств с убываю-
щей функцией интенсивности отказов и
4,12,1 ÷=α
для механических устройств с
возрастающей функцией интенсивности отказов.
Распределение Вейбулла для времени до отказа системы возникает обычно
тогда, когда имеют место отказы различной физической природы (износ, старе-
ние, механические и электрические перегрузки и т.п.).
Пример 3.2. Пусть вероятность безотказной работы ВС за время
1000=t
ч со-
ставляет
99,0)1000(
=
P . Составить прогноз вероятности безотказной работы этой
же системы через 100000 ч работы без обслуживания по экспоненциальной моде-
ли и модели Вейбулла.
Решение
а). В случае выбора экспоненциальной модели
3
10
)1000(
⋅
−
=
λ
eP
, откуда оп-
ределим интенсивность отказов ВС:
3
10
99,0
⋅
−
=
λ
e
;
(
)
3
10
ln99,0ln
⋅
−
=
λ
e
;
./110
10
10005,1
10
99,0ln
5
3
2
3
constч =≈
⋅−
−=−=
−
−
λ
Прогнозируемая вероятность безотказной работы через 10
5
часов:
.37,0)10(
15
5
10
5
10
===
−−
⋅
−
eeP
Э
б). В случае выбора модели Вейбулла
α
λ
−
⋅
=
3
10
0
)1000( eP
, где
α
принята
равной 0,5. Тогда
62,31
0
1000
0
99,0
⋅−
==
−
λλ
ee
, откуда
000318,0
62,31
10
62,31
99,0ln
2
0
≈−=−=
−
λ
.
Прогнозируемая вероятность безотказной работы через 10
5
ч:
904,0)10(
5,0
)
5
10(000318,0
5
==
⋅−
eP
В
.
Следовательно, прогнозируемые показатели надежности работы объекта за-
висят от правильно выбранной модели.
24
Выбор модели надежности – сложная научно-техническая задача. Она может
быть решена методами математической статистики, если имеется большой стати-
стический материал об отказах исследуемой системы. Ввиду высокой надежности
ИС и ее компонентов, как правило, статистических данных об отказах немного. В
последнем случае при выборе модели руководствуются результатами ускоренных
испытаний, физическими соображениями, предыдущим опытом.
В случае приближенных оценок часто выбирается экспоненциальная модель
как наиболее удобная с точки зрения аналитических преобразований. Эту модель
рекомендуется использовать при выполнении расчетов надежности при отсутст-
вии других исходных данных, кроме интенсивностей отказов. В случае наличия
более полных исходных данных целесообразно пользоваться более точными мо-
делями, например, моделью Вейбулла.
Вероятностные процессы. Если случайная величина изменяется в процессе
опыта, то возникает случайная функция - функция, которая может принимать тот
или иной вид, заранее не известный. Если аргументом случайной функции явля-
ется время, то такая случайная функция называется вероятностным или случай-
ным процессом. Функционирование любой технической системы, в том числе ИС,
представляет собой реализацию вероятностных процессов, так как процесс смены
состояний объекта - это следствие потоков отказов и потоков восстановлений.
Чтобы охарактеризовать вероятностный процесс, необходимо указать тип
процесса и его числовые характеристики. Наиболее часто для описания процес-
сов, происходящих в системах, используется марковский процесс.
Марковский процесс - это процесс, у которого для каждого момента времени
вероятность любого состояния объекта в будущем зависит только от состояния
объекта в данный момент и не зависит от того, каким образом объект пришел в
это состояние.
Необходимым условием для марковского процесса является экспоненциаль-
ное распределение времени работы до отказа и времени восстановления работо-
способности. Важнейшая числовая характеристика такого процесса - вероятность
перехода объекта в то или иное состояние за заданный промежуток времени. Зная
это, можно определить вероятности каждого из возможных состояний объекта.
Пусть объект, состоящий из двух параллельно работающих элементов, может
находиться в состояниях 0, 1 и 2 (рис. 3.2). Состояние 0 - оба элемента, входящие
в объект, работоспособны; состояние 1 - один из элементов находится в отказовом
состоянии; состояние 2- оба элемента находятся в отказе. Из i-го состояния в j-е
объект переходит с постоянной интенсивностью
ij
λ
, обратно - с постоянной ин-
тенсивностью
ji
µ
.

25
2
1
а
)
0 1
λ
01
µ
10
2
λ
12
µ
21
б
)
Рис. 3.2. Схема
р
езе
р
ви
р
ованного объекта
(
а
)
и г
р
а
ф
его состояний
(
б
)
.
Составим уравнения для определения вероятностей каждого из состояний
марковского процесса в рассматриваемом объекте (дифференциальные уравнения
А.Н. Колмогорова).
(3.10)
).()(
);()()()(
);()(
112221
2
22100111012
1
110001
0
+−=
+++−=
+−=
tPtP
dt
dP
tPtPtP
dt
dP
tPtP
dt
dP
λµ
µλµλ
µλ
В практике расчетов надежности систему уравнений Колмогорова можно
получить непосредственно по виду графа состояний объекта, если пользоваться
следующим правилом: для каждого из возможных состояний объекта записы-
вается уравнение, в левой части которого
dtdP
i
/
, а в правой - столько слагае-
мых, сколько стрелок графа соприкасается с данным состоянием. Если
стрелка направлена в данное состояние, то перед слагаемым ставится знак
плюс, если стрелка направлена из данного состояния - знак минус. Каждое
слагаемое равно произведению интенсивности перехода из данного состоя-
ния (либо в данное состояние) на вероятность состояния, из которого выхо-
дит стрелка.
Решение системы (3.10) можно получить по известным правилам решения
системы дифференциальных уравнений. Однако его можно существенно упро-
стить, если учесть, что рассматривается стационарный марковский процесс, для
которого
0)( =tdP
i
(вероятности состояний не меняются с течением времени). То-
гда
(3.11)
,1
;0
;)(0
;0
210
112221
22111012001
110001
=++
+−=
++−=
+−=
PPP
PP
PPP
PP
λµ
µµλλ
µλ
где последнее уравнение
∑
=
=
2
0
1
i
i
P
называется нормировочным условием, ко-
торое обусловлено тем, что первые три уравнения сводятся к двум (при трех не-
известных).
Решив систему линейных алгебраических уравнений (3.11), например, ме-
тодом Гаусса, найдем вероятности состояний системы.
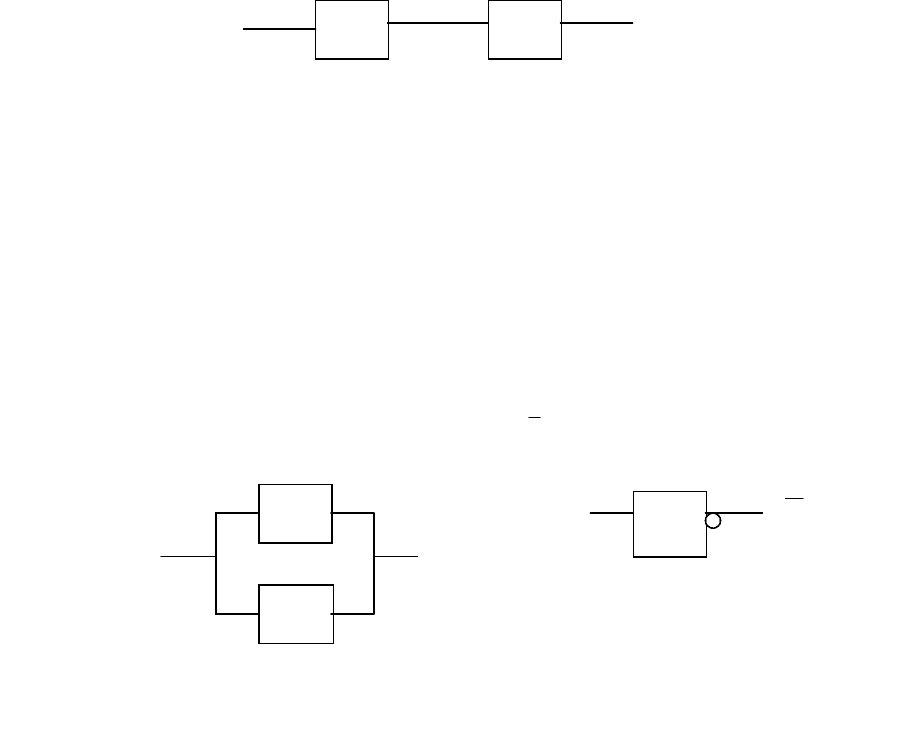
26
Лекция 9.
2.2.1 РАСЧЕТ НАДЕЖНОСТИ С ИСПОЛЬЗОВАНИЕМ ЭЛЕМЕНТОВ
МАТЕМАТИЧЕСКОЙ ЛОГИКИ
Расчет надежности сложного объекта, по существу, является определением
истинности сложного высказывания. Использование аппарата математического
логики позволяет формализовать условия работоспособности сложных структур и
получать формулы для расчета надежности.
1. Если о системе можно утверждать, что она работоспособна, если рабо-
тоспособны ее элементы a и b, то можно сделать вывод о том, что работоспособ-
ность системы (событие с) и работоспособности элементов a и b (событие a и со-
бытие b) связаны между собой логическим уравнением работоспособности:
bac
∧=
.
Логическое уравнение работоспособности для данного случая может быть
представлено схемой последовательного соединения элементов a и b (рис. 3.3).
a b
Рис. 3.3. Схема последовательного соединения элементов.
2. Если о системе можно утверждать, что она работоспособна, если рабо-
тоспособны ее элемент a или элемент b, можно сделать вывод о том, что работо-
способность системы (событие c) и работоспособности элементов a и b (событие a
и событие b) связаны между собой логическим уравнением работоспособности:
bac
∨=
.
Этому уравнению соответствует схема параллельного соединения элементов
a и b (рис. 3.4).
3. Если работоспособное состояние элемента обозначить через a , то нерабо-
тоспособное состояние этого элемента будет
a
. Логическое отрицание может
быть отражено в виде схемы инвертора (рис. 3.5).
a
b
a
a
Рис. 3.4. Схема параллельного
сое
д
инения элементов.
Рис. 3.5. Схема инвертирования
4. Логические операции конъюнкции, дизъюнкции и отрицания - основные
операции, используемые в теории надежности, так как к ним могут быть сведены
все другие логические операции.

27
5. Сложную логическую функцию можно минимизировать, т.е. преобразо-
вать таким образом, что она будет содержать минимальное число членов.
6. Логические функции можно преобразовать в алгебраические функции, ес-
ли заменить все логические операции арифметическими по следующим правилам:
bababa ⋅−+=∨ ; baba ⋅=∧ ; aa −= 1 .
Логическая функция работоспособности
∧
F
, у которой все логические опе-
рации заменены арифметическими, называется функцией работоспособности,
представленной в арифметическом виде
a
F .
Последовательность расчета надежности с использованием логических
схем. Чтобы получить формулу для вероятности работоспособного состояния
сложного объекта (функцию надежности), необходимо:
1) сформулировать словесно условие работоспособности системы;
2) на основании словесной формулировки записать логическую функцию
работоспособности
∧
F
;
3) минимизировать
∧
F
(исключить повторяющиеся члены);
4) в логической функции работоспособности заменить логические опера-
ции арифметическими, т.е. получить функцию
а
F ;
5) в арифметической функции работоспособности заменить простые со-
бытия (простые высказывания) их вероятностями;
6) в полученную формулу, дающую связь между вероятностями состояний
элементов системы и вероятностью состояния системы, подставить числовые зна-
чения вероятностей состояний элементов. Решением полученного уравнения яв-
ляется численное значение вероятности работоспособного состояния сложной
системы.
Пример 3.3. Определить вероятность работоспособного состояния
тракта передачи данных (рис. 3.6) при условии, что вероятности работоспо-
собных состояний элементов a, b, d, e равны по 0,9, а элемента с - 0,8.
а d
b е
c
Рис. 3.6. Структура тракта передачи данных
типа «мостик».
Решение
1). Словесная формулировка минимально необходимых условий работо-
способности тракта передачи данных: «тракт работоспособен, если работоспособ-
ны элементы a и d или элементы a, c и e или элементы b, c и d или элементы b и e.

28
2). На основании словесной формулировки запишем логическую функцию
работоспособности в следующем виде:
()
)()()(
ebdcbecadaF
л
∧∨∧∧∨∧∧∨∧=
.
3). Разложим функцию
л
F
с целью исключения повторяющихся членов
(3.12):
{}{}
beadcbebdaeadcF
л
∨∨∨∨∨=
.
Упростим логическое выражение в первых фигурных скобках:
).)(()()( baededbeda ∨∨=∨∨∨
В окончательном виде логическая функция работоспособности имеет сле-
дующий вид:
{}{}
.))(( beadcbaedcF
л
∨∨∨∨=
4). Заменим логические операции арифметическими:
{}
))(1())((
adbebeadcabbadeedcF
а
−+−+−+−+=
.
5). Заменим события a, b, c, d, e их вероятностями и определим количест-
венное значение вероятности работоспособного состояния тракта:
{}
{}
.977,0)81,081,081,0(2,0)81,08,1)(81,08,1(8,0
))(1())((
2
=−++−−=
=−+−+−+−+=
ebdaebdacededbabac
PPPPPPPPPPPPPPPPPPP
2.2.2 РАСЧЕТ НАДЕЖНОСТИ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ
Как уже отмечалось ранее, в качестве показателей надежности восстанав-
ливаемых объектов используются параметр потока отказов
)(t
ω
, вероятность без-
отказной работы в течение наработки
()
)(,0 tPt
−
, коэффициент готовности
)(tK
Г
,
коэффициент вынужденного простоя системы
)(tK
П
.
Нерезервированная система может находиться в произвольный момент
времени
t
в одном из двух состояний: 0 - система работоспособна; 1 - система не-
работоспособна и находится в ремонте.
Если обозначить вероятности этих состояний через
)(
0
tP
и
)(
1
tP
, то, оче-
видно, что )()(
0
tPtK
Г
=
и
)()(
1
tPtK
П
=
. При длительной эксплуатации
)(
∞→
t
могут
быть достигнуты установившиеся значения
0
PK
Г
=
,
1
PK
П
=
.
Если время безотказной работы и время восстановления имеют показа-
тельное распределение, то для вычисления функций готовности и простоя систе-
мы можно применить марковскую модель. Тогда в соответствии с графом состоя-
ний системы (рис. 3.11) имеем следующую систему дифференциальных уравне-
ний:
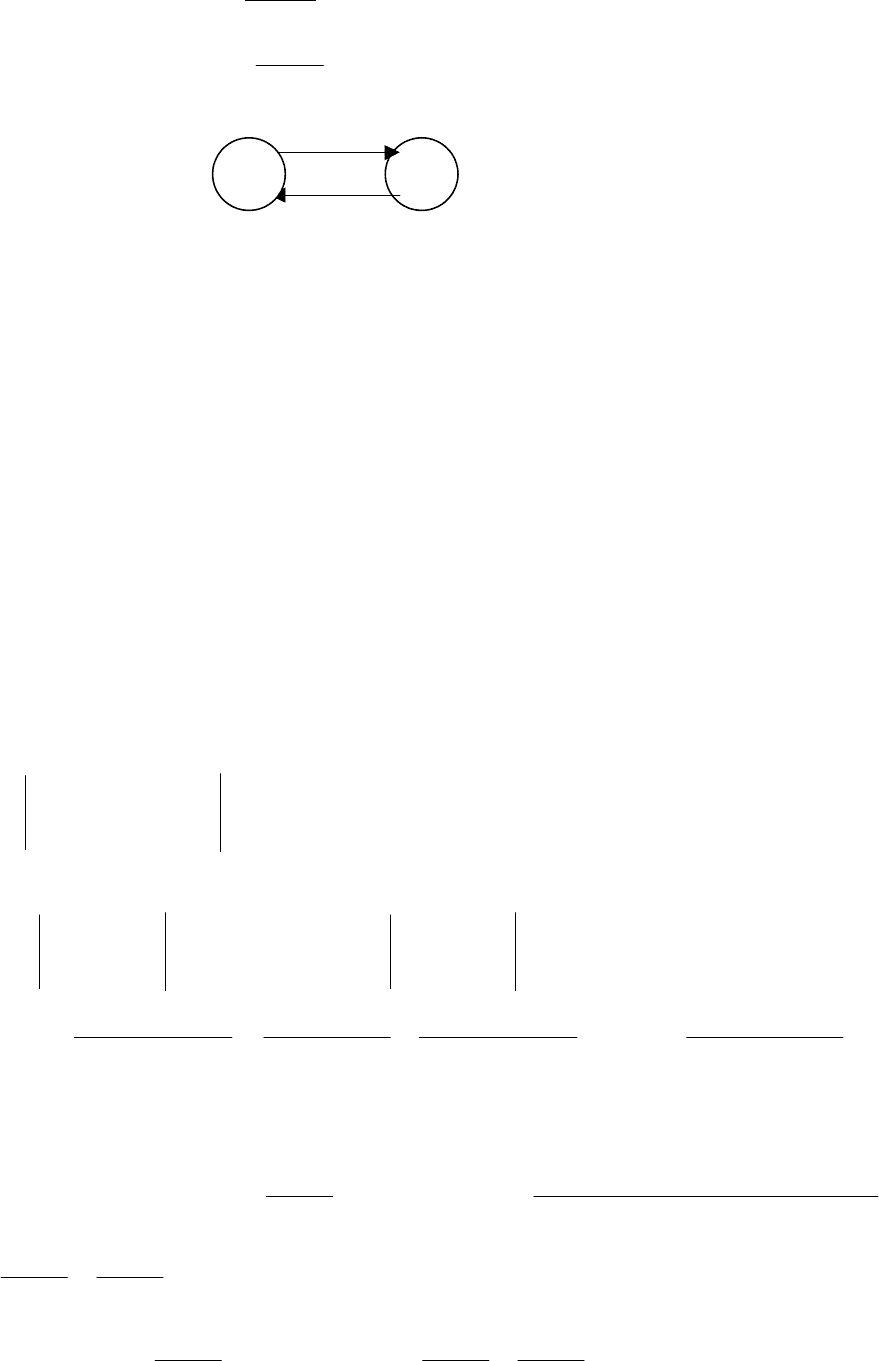
29
−=
+−=
).()(
)(
);()(
)(
10
1
10
0
tPtP
dt
tdP
tPtP
dt
tdP
µλ
µλ
(3.15)
1
λ
0
µ
Рис. 3.11. Граф состояний
нерезервированной ремонтируемой
системы:
λ
- интенсивность
отказов;
µ
- интенсивность
Если при
0
=
t
система находилась в работоспособном состоянии, то
начальные условия
1)0(
0
=
P
,
0)0(
1
=
P
. Используя преобразования Лапласа,
получим:
−=−
+−=−
).()(0)(
);()(1)(
101
100
SPSPSSP
SPSPSSP
µλ
µλ
или
=++−
=−+
.0)()()(
;1)()()(
10
10
SPSSP
SPSPS
µλ
µλ
Решим систему по формулам Крамера:
()
[]
;)(
))((
)(
)(
2
2
λµλµ
λµλµλµµλ
µλ
µλ
++=++=
=+++=−++=
+−
−+
=∆
SSSS
SSSSS
S
S
µ
µ
µ
+=
+
−
=∆ S
S )(0
1
1
; .
0
1)(
2
λ
λ
λ
=
−
+
=∆
S
()
[]
() ()
[]
;
1
)(
0
λµ
µ
λµλµ
µ
++
+
++
=
++
+
=
SSSSS
S
SP
()
[]
λµ
λ
++
=
SS
SP )(
1
.
Переходя от изображений к оригиналам (обратное преобразование Лапла-
са), получим:
()
(3.16) .
)(
)()(
)(
)()(
)(0)(
0
t
tt
ttt
Г
e
ee
eeetPtK
λµ
λµλµ
λµλµ
λµ
λ
λµ
µ
λµ
µµλµ
λµ
µ
+−
+−+−
+−⋅−+−
+
+
+
=
=
+
−++
=−
+
+==
()
(3.17) .)()(
)()(0
1
ttt
П
eeetPtK
λµλµ
λµ
λ
λµ
λ
λµ
λ
+−+−⋅−
+
−
+
=−
+
==
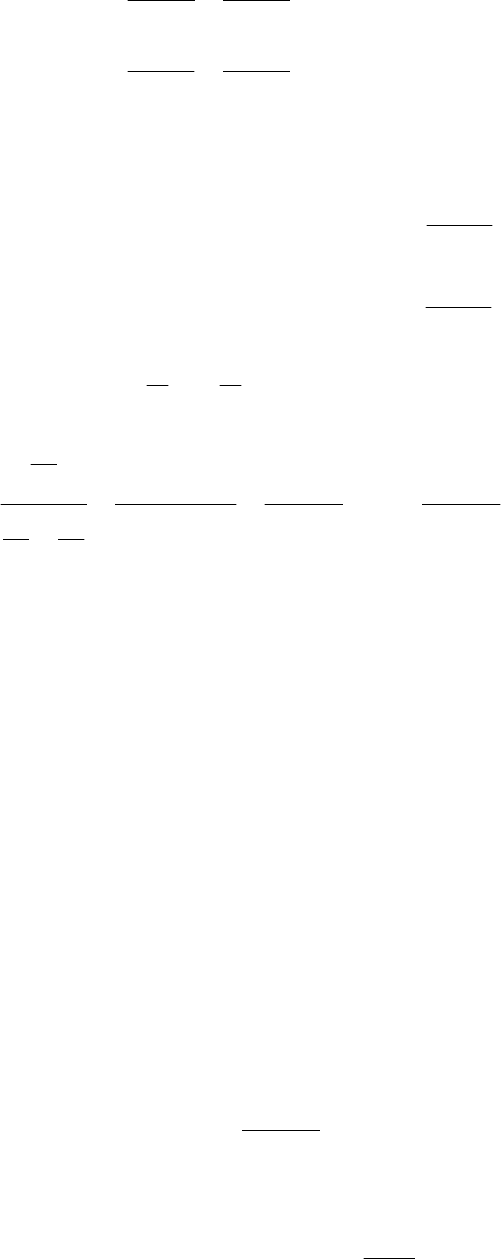
30
Если при 0
=
t
система находилась в ремонте, то 0)0(
0
=
P , 1)0(
1
=
P и
результатом решения системы (3.15) будет:
+
+
+
==
+
−
+
==
+−
Π
+−
.)()(
;)()(
)(
1
)(
0
t
t
Г
etPtK
etPtK
λµ
λµ
λµ
λ
λµ
λ
λµ
λ
λµ
µ
При длительной эксплуатации получим стационарные значения коэффи-
циентов готовности и простоя, не зависящие от начальных условий:
.
;
1
0
λµ
λ
λµ
µ
+
==
+
==
PK
PK
П
Г
Поскольку
ВР
tt
1
,
1
==
µλ
, то приходим к уже известным выражениям:
ВР
В
ВР
Р
ВРВ
РВ
РВ
В
tt
t
K
tt
t
ttt
tt
tt
t
K
+
=
+
=
+
=
+
=
ΠΓ
;
)(
11
1
, т.е. коэффициент готовности
характеризует долю времени, в течение которого система работоспособна, а ко-
эффициент простоя - долю времени, в течение которого она восстанавливается
(ремонтируется).
Если система имеет несколько работоспособных состояний, то функция
готовности системы определяется как
∑
=
=
n
i
iГ
tPtK
1
)()(, где
n
- число работоспособных состояний;
)(tP
i
- вероят-
ность i-го работоспособного состояния.
Пример 3.6. Восстанавливаемая система с показательным законом
распределения времени безотказной работы и времени восстановления имеет
коэффициент готовности
95,0
=
Г
K
.
Вычислить вероятность безотказной работы системы в течение наработки
(0,10) ч, если среднее время восстановления
5
=
В
t
ч.
Решение
Из соотношения
95,0=
+
=
ВР
p
Г
tt
t
K
находим значение наработки на отказ:
()
РРРВРГ
tttttK
=+=+
75,495,0 ;
;
95
05,0
75,4
==
Р
t ч.
