Xing Zh., Zhou Sh. Neutrinos in Particle Physics, Astronomy and Cosmology
Подождите немного. Документ загружается.


406 11 Cosmological Matter-antimatter Asymmetr
y
n
B
=
1
6
T
2
N
f
i
=
1
(
2
μ
Q
i
+
μ
U
i
+
μ
D
i
)
,
n
L
=
1
6
T
2
N
f
i
=
1
(
2
μ
i
+
μ
E
i
)
,
(
11.83
)
where the summation over the color
q
uantum number of
q
uarksisim
p
lied
.
O
n the other hand, the reactions in chemical equilibrium allow the chemica
l
p
otentials to relate to one another. First, all the Yukawa interactions at a
temperature below TeV are fast enough to guarantee
μ
Q
i
+
μ
H
−
μ
U
i
=0
,
μ
Q
i
−
μ
H
−
μ
D
i
=0
,
μ
i
−
μ
H
−
μ
E
i
=0
,
(
11.84
)
where we have assumed the Higgs doublets to have a common chemical po-
tential
(
i.e.,
μ
H
i
=
μ
H
)
. Furthermore, the mixing of quark flavors arisin
g
from the non-diagonal Yukawa couplings can make the chemical potentials of
i
q
uarks flavor-independent
(
i.e.,
μ
Q
i
=
μ
Q
,
μ
U
i
=
μ
U
a
nd
μ
D
i
=
μ
D
)
. Second
,
the hypercharge conservation requires
i
N
f
N
(
μ
Q
−
2
μ
U
−
μ
D
)
−
i
(
μ
i
+
μ
E
i
)
+2
N
H
N
μ
H
=0
.
(
11.85
)
F
inally, the sphaleron processes turn all the left-handed fermions into the
vacuum state.
A
saconse
q
uence
,
3
N
f
N
μ
Q
+
i
μ
i
=
0
.
(
11.86
)
With the help of Eqs.
(
11.84
)
,
(
11.85
)
and
(
11.86
)
, all the chemical potential
s
c
an be expressed in terms o
f
the
N
f
N
-
in
d
epen
d
ent ones. It is t
h
en eas
y
t
o
rewrite the lepton and baryon numbers as
(
Harvey and Turner, 1990
)
n
B
=+
1
6
T
2
8
N
f
N
+4
N
H
N
2
N
f
N
+3
N
H
N
i
μ
E
i
,
n
L
=
−
1
6
T
2
14
N
f
N
+
9
N
H
N
2
N
f
N
+3
N
H
N
i
μ
E
i
.
(
11.87
)
This result leads to the
f
ollowin
g
relation between
B
and
(
B
−
L
):
n
B
=
8
N
f
N
+4
N
H
N
22
N
f
N
+13
N
H
N
(
n
B
−
n
L
)
≡
c
(
n
B
−
n
L
)
.
(
11.88
)
In the
S
Mweobtai
n
c
=
28
/
79
f
rom
N
f
N
= 3 and
N
H
N
=1.Eq.
(
11.88
)
i
mplies that the
(
B
−
L
)
number was first generated in the leptogenesis era

1
1.3
B
aryogenesis via
L
eptogenesis 40
7
a
n
d
t
h
en reprocesse
d
into t
h
e
b
ar
y
on num
b
er
by
t
h
esp
h
a
l
eron interactions.
The above relation depends on the assumption that the electroweak
g
au
ge
s
ymmetry is restored and the chemical potentials of gauge bosons are van
-
i
shin
g
.I
f
this assumption is relaxed durin
g
or below the electroweak phas
e
transition and only the electric charge neutrality is imposed, the
n
c
=
1
2
/
3
7
c
an be obtained
(
Harvey and Turner, 1990
)
. After the sphaleron processes
g
oouto
f
equilibrium, there are no more interactions that can chan
g
ethe
bar
y
on number as
y
mmetr
y
Y
B
YY
≡
(
n
B
−
n
B
)
/s
.
Hence
Y
B
YY
generated at th
e
t
em
p
era
t
ur
e
T
∗
∼O
(
1
0
2
)
GeV keeps unchanged until today. On the other
h
an
d
,t
h
e
b
aryon-to-p
h
oton ratio
η
is re
l
ate
d
t
o
Y
B
YY
th
roug
h
η
≡
n
B
−
n
B
n
γ
=
s
n
γ
Y
B
YY
=
˜
g
∗
π
4
45
ζ
(
3
)
Y
B
YY
≈
1
.
8˜
g
∗
Y
B
YY
,
(
11.89
)
where Eqs.
(
9.24
)
and
(
11.60
)
are used. The effective number of relativisti
c
degrees of freedom ˜
g
∗
can be computed by means of Eq.
(
11.61
)
. The present
-
day value of ˜
g
∗
gets contributions only from the photons with
T
∗
b
TT
=
T
γ
TT
=
T
a
n
d
t
h
e neutrinos wit
h
T
∗
f
TT
=
T
ν
TT
=
(4
/
11
)
1
/
3
T
γ
TT
; namely, ˜
g
∗
(
T
)
=2+7
/
8
×
3
×
2
×
4
/
11
≈
3
.
9
1.
S
owehave
η
≈
7
.
04
Y
B
YY
(
and
n
B
=0
)
today. The value
of
η
at
T
∗
∼O
(
10
2
)
GeV can be given in terms of today’s value of
η
at
T
;
i
.e.,
η
(
T
∗
)
/η
(
T
)=˜
g
∗
(
T
∗
)
/
˜
g
∗
(
T
)
≈
2
7
.
3, where ˜
g
∗
(
T
∗
)=
g
∗
(
T
∗
)
=10
6
.
7
5i
n
the SM has been in
p
ut.
To assu
r
ethe
N
1
NN
decay to be out o
f
thermal equilibrium, we require tha
t
i
ts deca
y
rat
e
Γ
1
ΓΓ
be smaller than the Hubble
p
aramete
r
H
a
tthetem
p
erature
T
=
M
1
.
With the help of Eqs.
(
9.31
)
and
(
11.36
)
, one may express th
e
requ
i
rement
Γ
1
ΓΓ
<H
(
T
=
M
1
)
as
(
M
†
D
MM
M
D
MM
)
11
M
1
≡
˜
m
1
<
m
∗
≡
?
64
g
∗
π
5
45
·
v
2
M
Pl
MM
≈
1
.
08
×
10
−
3
eV
.
(
11.90
)
where ˜
m
1
an
d
m
∗
are referred to as the effective neutrino mass and th
e
equilibrium neutrino mass
(
Buchm¨uller et a
l
., 2005a
)
, respectively. Note tha
t
the value of ˜
m
1
determines not onl
y
the rates o
f
th
e
N
1
NN
d
eca
y
an
d
its inverse
d
eca
y
but also the rates of the
Δ
L
= 1 scatterin
g
processes, as indicated in
E
qs.
(
11.70
)
and
(
11.76
)
.
Let us brie
fl
y reiterate the spirit o
f
baryo
g
enesis via lepto
g
enesis in th
e
t
y
pe-I seesaw mechanism wit
h
M
1
M
2
M
M
an
d
M
1
M
3
M
M
.
First, the le
p
ton
n
um
b
er asymmetry
Y
L
Y
Y
can be produced by the CP-violating and out-of-
equilibrium decays o
f
the li
g
htest heavy Majorana neutrin
o
N
1
NN
.T
he evolut
i
on
of
Y
L
YY
i
s governed by the Boltzmann equations in Eq.
(
11.82
)
. Second, th
e
efficient sphaleron interactions convert
Y
L
YY
into t
h
e
b
aryon num
b
er asymmetr
y
Y
B
Y
Y
,andthee
ffi
cienc
y
o
f
this conversion is essentiall
y
determined b
y
c
=
28
/
7
9inEq.
(
11.88
)
. Third, the baryon-to-photon ratio
η
can be diluted
by the decreasing number of relativistic degrees of freedom ˜
g
∗
f
r
om
T
∗
∼
O
(
10
2
)
GeVtotoday,asshowninEq.
(
11.89
)
. Finally, today’s baryon numbe
r
a
symmetry is approximately given by
(
Buchm¨uller et al., 2005a
)

408 11 Cosmological Matter-antimatter Asymmetr
y
η
≈−
0
.
96
×
10
−
2
ε
1
κ
f
,
(
11.91
)
where
ε
1
denotes the CP-violating asymmetry in the
N
1
NN
d
ecays an
d
κ
f
i
san
e
ffi
ciency
f
actor measurin
g
the washout e
ff
ects on
Y
L
YY
.
In
the weak washout
regime ˜
m
1
<m
∗
,
the final bar
y
on number as
y
mmetr
y
sensitivel
y
depends
on the initial number density of heavy Majorana neutrinos. In the stron
g
washout regime ˜
m
1
>
m
∗
,
the
fi
nal result o
f
η
is independent o
f
the initial
c
onditions and the efficienc
y
facto
r
κ
f
can be expressed as
(
Buchm¨uller
e
t
al.
,
2004
;
Giudic
e
e
ta
l
., 2004
)
κ
f
≈
(2
±
1
)
×
10
−
2
0
.
01 e
V
˜
m
1
1
.
1
±
0
.
1
.
(
11.92
)
This empirical result is a good approximation to the solution to the full set o
f
Boltzmann equations. By assuming a successful leptogenesis mechanism and
u
sin
g
current experimenta
ld
ata on neutrino osci
ll
ations, one may set a
l
ower
bound on the magnitude of
M
1
(
Davidson and Ibarra, 2002; Buchm¨ulle
r
et
al.
,
2004
)
. However, such a bound will be modified if the contributions from
h
eavier Ma
j
orana neutrinos and di
ff
erent lepton
fl
avors are taken into account
(
Davidson et al., 2008
)
.
11.4 Recent Developments
i
n Leptogenes
i
s
The leptogenesis mechanism has been extensively studied since it was first
propose
db
y Masata
k
aFu
k
ugita an
d
Tsutomu Yanagi
d
a in 1986, an
d
now it
s
c
ontent
h
as
b
ecome very sop
h
isticate
d
.InFu
k
u
g
ita an
d
Yana
g
i
d
a
’
sori
g
ina
l
paper, the one-loop vertex corrections to heav
y
Ma
j
orana neutrino deca
ys
were calculated and the baryon number asymmetry was estimated
(
Fukugita
a
nd Yanagida, 1986
)
. Later on, the Boltzmann equations for the evolution o
f
the lepton number asymmetry were derived
(
Luty, 1992
)
, and the importanc
e
of the self-energy corrections to heavy Majorana neutrinos was realized
(
Li
u
a
nd
S
e
g
re, 1994; Flan
z
et al
.
,
1995;
C
ovi
et al
., 1996
)
. The latter contribution
to CP violation may even dominate in some cases
(
Pilaftsis, 1997a, 1997b
)
.I
n
this section we shall introduce some recent developments in leptogenesis:
(
a
)
the lepto
g
enesis mechanism in the type-II or type-III seesaw model, where
h
eavy triplet scalars or fermions are introduced;
(
b
)
the resonant leptogenesis
m
echanism, in which
C
P violation can be resonantl
y
enhanced i
f
there ar
e
two nearly degenerate heavy Majorana neutrinos;
(
c
)
the soft leptogenesis
m
echanism, which works in a supersymmetric version of the type-I seesa
w
m
odel; and
(
d
)
the flavor-dependent leptogenesis mechanism.
11.4.1 Tr
i
plet Leptogenes
i
s
It is known that the unique dimension-5 Weinber
g
operator
f
or neutrino
m
asses can be derived at the tree-level from an extension of the SM b
y
1
1.4 Recent Deve
l
opments in Leptogenesis 40
9
add
in
gh
eavy
SU
(
2
)
L
s
in
gl
et neutrinos
,
SU
(
2
)
L
t
rip
l
et sca
l
ars or
SU
(
2
)
L
triplet fermions and allowin
g
lepton number violation. The first option is just
t
h
e type-I seesaw mec
h
anism an
d
correspon
d
stot
h
econventiona
l
Fu
k
ugita
-
Yana
g
ida scenario o
f
lepto
g
eneis. Here we discuss the main
f
eatures o
f
lepto
-
genesis induced by the triplet scalars. The leptogenesis mechanism associated
with the triplet fermions may similarly work
(
Hambye, 2004; Strumia, 2006
).
I
n the type-II seesaw mechanism the La
g
ran
g
ian o
f
neutrino mass term
s
a
ssociated with an SU
(
2
)
L
scalar tri
p
let
Δ
h
as been given in Eq.
(
4.7
)
,wher
e
the last two terms determine the lepton-number-violating decay modes of
Δ
a
n
d
Δ
(
i.e.
,
Δ
→
+
,
Δ
→
H
+
H
a
n
d
Δ
→
+
,
Δ
→
H
+
H
)
. Note that
there are no one-loop vertex corrections to the above deca
y
s, in contrast wit
h
the decays o
f
heavy Majorana neutrinos. Hence at least two triplet scalar
s
Δ
1
a
n
d
Δ
2
a
re needed to
g
enerate
C
P violation via the sel
f
-ener
g
y corrections
(
Ma and Sarkar, 1998
)
. The relevant Lagrangian can be written as
−L
=
1
2
2
a
=1
L
Y
Δ
Y
a
Δ
a
i
σ
2
c
L
−
2
a
=
1
λ
Δ
a
M
Δ
M
a
H
T
i
σ
2
Δ
a
H
+
h
.
c
.,
(
11.93
)
w
h
ere
Y
Δ
Y
a
are t
h
eYu
k
awa coup
l
ing matrices
,
λ
Δ
a
d
enote t
h
e
d
ou
bl
et-trip
l
et
H
iggs coup
l
ing constants, an
d
M
Δ
M
a
a
r
et
h
et
r
ee
-l
eve
lm
asses o
f
Δ
a
(
fo
r
a
=
1
,
2
)
. At the one-loop level
Δ
1
a
n
d
Δ
2
mix wit
h
eac
h
ot
h
er via t
h
e
l
epton an
d
H
iggs doublets, so their mass matrices are given by
(
Ma and Sarkar, 1998
)
M
2
=
M
2
Δ
M
1
−
i
Γ
11
ΓΓ
M
Δ
M
1
−
i
Γ
12
ΓΓ
M
Δ
M
2
−
i
Γ
21
ΓΓ
M
Δ
M
1
M
2
Δ
M
2
−
i
Γ
22
ΓΓ
M
Δ
M
2
,
(
11.94
)
w
h
e
r
e
Γ
11
Γ
Γ
a
n
d
Γ
22
ΓΓ
s
tand respectivel
yf
or the tree-level deca
y
rates o
f
Δ
1
a
n
d
Δ
2
,
and
Γ
ab
Γ
(
fo
r
a
,
b
=1
,
2
)
can be obtained by calculating the imaginary
parts o
f
the
Δ
b
→
Δ
a
t
ransition amp
l
itu
d
es
:
Γ
ab
ΓΓ
=
M
Δ
M
a
16
π
4
λ
Δ
a
λ
∗
Δ
b
+
Tr
Y
†
Δ
Y
a
Y
Δ
Y
b
.
(
11.95
)
It is strai
g
htforward to obtain the decay rates
Γ
11
ΓΓ
and
Γ
22
ΓΓ
b
y settin
g
a
=
b
i
nEq.
(
11.95
)
. After diagonalizing the mass matrix in Eq.
(
11.94
)
,onecan
fi
nd the correspondin
g
mass ei
g
enstates
Φ
1
a
n
d
Φ
2
,w
h
ic
h
are t
h
e
l
inea
r
s
u
p
er
p
ositions of
Δ
1
a
nd
Δ
2
.
One ma
y
similarl
y
consider the mass matri
x
f
o
r
Δ
1
an
d
Δ
2
,
and define the mass eigenstate
s
Φ
1
a
n
d
Φ
2
.
Although
Φ
a
a
n
d
Φ
a
have the same masses, they are not
C
Pei
g
enstates. The quantity
Γ
12
ΓΓ
is in
general complex. The asymmetries between the decays
Φ
a
→
+
and thei
r
CP-conjugate processes
Φ
a
→
+
are given by
(
Ma and Sarkar, 1998
)
ε
a
≡
2
Γ
(
Φ
a
→
+
)
−
Γ
(
Φ
a
→
+
)
Γ
(
Φ
a
→
+
)+
Γ
(
Φ
a
→
H
+
H
)
=
M
Δ
M
1
M
Δ
M
2
M
Δ
M
a
2
π
2
(
M
2
Δ
M
1
−
M
2
Δ
M
2
)
Γ
aa
Γ
Γ
Im
λ
Δ
1
λ
∗
Δ
2
Tr
Y
†
Δ
Y
2
Y
Δ
Y
1
,
(
11.96
)
410 11 Cosmological Matter-antimatter Asymmetr
y
whe
r
e
|
M
2
Δ
M
1
−
M
2
Δ
M
2
|
2
|
Γ
12
Γ
Γ
|
M
Δ
M
2
has bee
n
assu
m
ed a
n
dthesu
mm
at
i
o
n
over
the le
p
ton-flavor index is im
p
lied. Note that the factor “2” in the definition
of
ε
a
t
akes into account the fact that eac
h
Φ
a
→
+
d
ecay mo
d
e vio
l
ates
the lepton number by two units. The
C
P-violatin
g
and out-o
f
-equilibrium
d
eca
y
sof
Φ
a
g
enerate a net lepton number asymmetry, which can partly b
e
c
onverte
d
into t
h
e
b
aryon num
b
er asymmetry via t
h
esp
h
a
l
eron processes
.
A
lthou
g
h the basic in
g
redients of this lepto
g
enesis mechanism follow the stan
-
d
ard
p
icture, the interactions of tri
p
let scalars are
q
uite different from those
of heavy Majorana neutrinos. In particular, the triplet scalars charged unde
r
the
SU
(
2
)
L
g
roup may be involved with rapid
g
au
g
e interactions.
O
ne ca
n
a
lso use the Boltzmann e
q
uations to describe how the number densities of
the triplet scalars and the lepton number asymmetry evolve
(
Ma and Sarkar,
1
998
).
I
nthetype-
(
I+II
)
seesaw scenario both the scalar triplet
Δ
and heav
y
M
ajorana neutrinos
N
i
NN
c
ontri
b
ute to t
h
e
l
i
gh
t neutrino masses an
d
t
h
e
l
epto
n
n
umber asymmetry. The La
g
ran
g
ian relevant to the decays o
f
Δ
a
n
d
N
1
NN
reads
−
L
=
L
Y
ν
YY
˜
HN
R
N
N
+
1
2
L
Y
Δ
Y
Δ
i
σ
2
c
L
−
λ
Δ
M
Δ
M
H
T
i
σ
2
Δ
H +
h
.
c
.,
(
11.97
)
f
rom which one may immediately work out the total decay rates of heav
y
Ma
j
orana neutrino
s
Γ
i
ΓΓ
=(
Y
†
ν
YY
Y
ν
Y
Y
)
i
i
M
i
MM
/
(
8
π
)
and that of the triplet scalar
Γ
Δ
Γ
=
M
Δ
M
1
6
π
Tr
Y
†
Δ
Y
Y
Δ
Y
+4
λ
2
Δ
,
(
11.98
)
where a specific phase convention has been chosen to assur
e
λ
Δ
to be
r
eal.
A
s a consequence of the CPT invariance, the total deca
y
rates of
Δ
a
n
d
Δ
a
re equal
(
i.e.
,
Γ
Δ
Γ
=
Γ
Δ
Γ
)
. It is worth pointing out that the presence of
Δ
→
H
+
H
a
n
d
Δ
→
H
+
H
d
ecays is necessary
f
or
g
eneratin
g
a
C
P-violatin
g
a
s
y
mmetr
y
betwee
n
Δ
→
+
a
nd
Δ
→
+
decays. The type-
(
I+II
)
seesa
w
s
cenario yields the effective neutrino mass matrix
M
ν
M
M
≈
M
L
MM
−
M
D
MM
M
−
1
R
M
M
M
T
D
MM
,
a
sshownin
C
hapter 4.
O
ne ma
y
rewrite this mass
f
ormula as
M
ν
MM
≈
M
I
MM
+
M
II
MM
wit
h
M
I
M
M
≡−
M
D
MM
M
−
1
R
MM
M
T
D
MM
a
nd
M
II
MM
≡
M
L
MM
,
so as to em
p
hasize that it consists
of a pure type-I seesaw term and a pure type-II seesaw term. Note that
M
D
MM
=
Y
ν
YY
v
/
√
2a
n
d
M
L
MM
=
Y
Δ
Y
v
Δ
w
i
th
v
Δ
=
λ
Δ
v
2
/M
Δ
M
a
n
d
v
≈
2
46
G
eV
.
For simplicit
y
, let us consider the limit
M
1
M
Δ
M
o
r
M
1
M
Δ
M
,
wher
e
M
1
a
n
d
M
Δ
M
stand respectively for the mass of the lightest heavy Majoran
a
neut
r
i
n
o
N
1
NN
a
nd that o
f
the triplet scala
r
Δ
.In
the
M
1
M
Δ
M
c
ase on
ly
the CP-violating asymmetry arising from the leptoni
c
Δ
a
nd Δ
d
ecays i
s
relevant to the bar
g
o
g
enesis via lepto
g
enesis, since a
C
P-violatin
g
asymmetr
y
i
nduced b
y
th
e
N
1
NN
deca
y
s can be erased b
y
the
Δ
-induced le
p
ton-number-
violating processes. Unlike the pure triplet leptogenesis scenario discusse
d
ab
ove,
h
ere t
h
ere exist t
h
e
N
i
N
N
-me
d
iate
d
one-
l
oop vertex corrections to t
he
l
e
p
tonic
Δ
→
+
decay
(
see Fig. 11.9
)
. A straightforward calculation leads
u
sto
(
Hambye and Senjanovic, 2004; Hambye et a
l
., 2006
)

1
1.4 Recent Deve
l
opments in Leptogenesis 41
1
Δ
Δ
H
H
N
i
NN
Fig. 11.9 The Feynman diagrams for the leptoni
c
Δ
→
+
decay at the tree-
an
d
one-
l
oo
pl
eve
l
s, w
h
ere
N
i
NN
(
i
=
1
,
2
,
3
)
are heavy Majorana neutrinos
ε
Δ
≡
2
Γ
(
Δ
→
+
)
−
Γ
(
Δ
→
+
)
Γ
Δ
Γ
+
Γ
Δ
Γ
=
1
2
π
j
λ
Δ
M
j
M
M
Δ
M
I
m
Y
†
ν
YY
Y
Δ
Y
Y
∗
ν
YY
jj
Tr
Y
†
Δ
Y
Y
Δ
Y
+4
λ
2
Δ
ln
1+
M
2
Δ
M
M
2
j
M
.
(
11.99
)
G
ive
n
M
i
MM
M
Δ
M
,Eq.
(
11.99
)
can approximate to
(
Hamby
e
et al.
, 2006
)
ε
Δ
≈
M
Δ
M
2
π
v
2
B
B
H
Im
Tr
M
†
II
MM
M
I
MM
?
Tr
M
†
II
MM
M
II
MM
,
(
11.100
)
whe
r
e
M
I
M
M
≡−
M
D
MM
M
−
1
R
MM
M
T
D
MM
,
M
II
MM
≡
M
L
MM
,
B
a
n
d
B
H
s
tand respectivel
yf
or
the branchin
g
ratios o
f
Δ
→
+
an
d
Δ
→
H
+
H
d
eca
y
s. It is now eviden
t
that the CP-violating asymmetr
y
ε
Δ
will vanish if
B
H
=0h
o
ld
s.
I
n
the
M
1
M
Δ
M
c
ase, we
f
ocus on
C
P violation in th
e
N
1
NN
d
eca
y
sinstea
d
of th
e
Δ
d
ecays. The Feynman dia
g
rams for the one-loop corrections to the
d
ecay
N
1
NN
→
+
H
are shown in Fig. 11.10. Note that the contributions fro
m
F
ig. 11.10
(
a
)
and Fig. 11.10
(
b
)
have been evaluated in Eq.
(
11.57
)
,andthe
c
orresponding CP-violating asymmetry can be recast into the following form
:
ε
N
1
=
3
M
1
8
π
v
2
·
I
m
Y
†
ν
YY
M
I
MM
Y
∗
ν
YY
11
(
Y
†
ν
YY
Y
ν
YY
)
1
1
,
(
11.101
)
where
F
(
x
)
→
−
3
/
(2
x
)
has been taken fo
r
x
→
+
∞
(
i.e.,
M
1
M
2
MM
,M
3
MM
)
.
In comparison, the
C
P-violatin
g
asymmetry induced b
y
Δ
v
ia Fig. 11.10
(
c
)
i
s found to be
(
Hambye and Senjanovic, 2004; Antusch and King, 2004
)
ε
Δ
1
=
3
M
1
8
π
v
2
·
I
m
Y
†
ν
YY
M
II
MM
Y
∗
ν
Y
Y
1
1
(
Y
†
ν
YY
Y
ν
YY
)
1
1
.
(
11.102
)
The total
C
P-violatin
g
asymmetry is
ε
1
=
ε
N
1
+
ε
Δ
1
.N
ote that
ε
N
1
a
n
d
ε
Δ
1
a
r
e
p
ro
p
ortional t
o
M
I
MM
a
n
d
M
II
MM
,
respectivel
y
. Note also that the minimal t
y
pe
-
(
I+II
)
seesaw model with only one heavy Majorana neutrino and one triplet

412 11 Cosmological Matter-antimatter Asymmetr
y
N
1
N
N
H
N
i
NN
N
1
NN
H
N
i
N
N
H
N
1
NN
H
Δ
H
H
(
a
)(
b
)(
c
)
Fig. 11.10 The Feynman diagrams
f
or
N
1
→
+
H
a
t the one-loop level:
(
a
)
the self-energy correction;
(
b
)
the vertex correction mediated by heavy Majorana
n
eut
rin
os
N
i
NN
; (c) the vertex correction mediated by the triplet scalar Δ
s
calar can account
f
or both the mass spectrum o
f
three li
g
ht neutrinos an
d
the observed baryon number asymmetry
(
G
u
e
tal
.
,
2006
)
.Since
Δ
a
nd
Δ
a
r
e
i
nvolvedwithrapid
g
au
g
e interactions, their number densities may
f
ollow the
thermal equilibrium distribution such that the lepton number as
y
mmetr
y
i
s
essentially independent of the initial conditions
(
Hambye
e
tal., 2006
).
11.4.2 Resonant Leptogenes
i
s
S
o
f
ar we have assumed that three heavy Majorana neutrinos have a stron
g
m
ass hierarchy
(
i.e.,
M
1
M
2
MM
,M
3
MM
)
. It has been pointed out that the CP-
violating asymmetry arising from the one-loop self-energy corrections can b
e
resonantl
y
enhanced provided the masses o
f
two or three heav
y
Ma
j
orana
n
eutrinos are nearly degenerate
(
Pilaftsis, 1997a, 1997b; Pilaftsis and Un-
d
erwood, 2004
)
. If the difference betwee
n
M
i
MM
a
n
d
M
j
M
i
scompara
bl
ewit
h
the deca
y
widths o
f
N
i
NN
a
n
d
N
j
N
(
i.e.,
|
M
i
MM
−
M
j
M
|
∼
Γ
i
ΓΓ
,Γ
j
Γ
)
, then the con
-
ventional perturbation field theor
y
should not work here. For instance, the
CP-violating asymmetr
y
ε
s
i
o
btained in Eq.
(
11.46
)
is apparently divergent
at
M
i
MM
=
M
j
M
. A proper way to deal with this problem is as follows
(
Flanz
et
a
l
.
,
1995; Buchm¨uller and Pl¨umacher, 1998; Pl¨umacher, 1998
)
:
(
a
)
we first
c
alculate the amplitude o
f
+
H
↔
+
H
scatterin
g
me
d
iate
db
y
N
i
N
N
in
t
h
e
s
-
channel;
(
b
)
the resummed propagators of
N
i
NN
ca
n
be w
ri
tte
nin
t
h
e
m
atrix form as
S
i
j
(
/
p
//
)
, whose non-diagonal elements come from the transi
-
tion amplitudes o
f
N
j
N
→
N
i
NN
;
(
c
)
expandin
g
S
ij
(
/
p
//
)
around the complex poles
√
s
i
=
M
p
o
l
e
i
MM
−
i
Γ
po
le
i
ΓΓ
/
2wit
h
M
p
o
l
e
i
M
M
a
n
d
Γ
p
o
le
i
ΓΓ
being the physical masses and
d
ecay widths, one can define the effective couplings of the interaction ver
-
t
i
ces of
N
i
NN
→
+
H
a
n
d
N
i
NN
→
+
H
.
Then the
C
P-violatin
g
asymmetry can
be directly figured out by using these effective couplings
(
Pilaftsis, 1997b;
P
ilaftsis and Underwood, 2004
):
ε
i
=
Im
(
Y
†
ν
YY
Y
ν
YY
)
2
ij
(
Y
†
ν
Y
Y
Y
ν
YY
)
i
i
(
Y
†
ν
Y
Y
Y
ν
YY
)
jj
·
(
M
2
i
MM
−
M
2
j
M
)
M
i
MM
Γ
j
Γ
(
M
2
i
MM
−
M
2
j
M
)
2
+
M
2
i
MM
Γ
2
j
Γ
,
(
11.103
)
w
h
e
r
e
i
=
j
. Note that this result is onl
y
applicable to the case o
f
two nearl
y
d
egenerate heavy Majorana neutrinos. It is worth remarking that two heavy

1
1.4 Recent Deve
l
opments in Leptogenesis 41
3
Majorana neutrinos are su
ffi
cient
f
or
g
eneratin
g
the li
g
ht neutrino masses
a
nd explainin
g
the baryon number asymmetry in the minimal type-I seesaw
m
odel
(
Frampto
n
e
ta
l
.
,
2002; Guo and Xing, 2004; Guo et a
l.
, 2007
)
.Th
e
d
eca
y
wi
d
t
h
Γ
j
Γ
a
ppearing in Eq.
(
11.103
)
serves as a regulator, which make
s
the CP-violating asymmetry
ε
i
w
ell-behaved in th
e
M
i
MM
=
M
j
M
l
imit. It is
obv
i
ous that
ε
i
∼
O
(
1
)
can be obtained when the condition
s
Im
(
Y
†
ν
YY
Y
ν
YY
)
2
ij
(
Y
†
ν
Y
Y
Y
ν
YY
)
ii
(
Y
†
ν
YY
Y
ν
YY
)
j
j
∼O
(
1
)
,
M
i
MM
−
M
j
M
=
1
2
Γ
j
ΓΓ
(
11.104
)
a
re satis
fi
ed. This resonant lepto
g
enesis mechanism provides us with an in
-
terestin
g
possibility to lower the masses o
f
N
i
NN
down to the TeV scale or eve
n
the electroweak scale
(
Pilaftsis, 2005; Pilaftsis and Underwood, 2005
).
I
n a via
bl
e resonant
l
epto
g
enesis scenario, t
h
erequire
d
mass
d
e
g
eneracy
|
M
i
MM
−
M
j
M
|
/M
j
M
is usuall
y
o
f
O
(
10
−
7
)(
Xing and Zhou, 2007
)
. Such a high de-
gree of degeneracy may arise from the flavor symmetry breaking or radiativ
e
c
orrections, i
f
M
i
MM
=
M
j
M
h
o
ld
sint
h
e symmetry
l
imit or at a super
h
i
gh
ener
g
y
s
cale
(
Pilaftsis and Underwood, 2004, 2005; Turzynski, 2004; Gonzalez Felip
e
et a
l
.
,
2004;
J
oaquim, 2005;
B
ranc
o
e
ta
l.
,
2006
).
11.4.3 Soft Lepto
g
enesi
s
The idea o
f
lepto
g
enesis can be directly applied to the supersymmetric seesa
w
m
odels
(
Giudice
e
tal
.
,
2004
)
. In this case one has to take into account the
C
P-violatin
g
asymmetries arisin
gf
rom the decays o
f
supersymmetric part
-
n
ers o
f
heav
y
Ma
j
orana neutrinos, denoted as
˜
N
i
NN
,and
f
rom some new deca
y
m
odes with supersymmetric particles in the final states and running in th
e
l
oops. The overall
C
P-violatin
g
asymmetry
f
rom the
N
i
NN
(
or
˜
N
i
NN
)
decays is
a
pproximately twice as lar
g
e as that in a conventional seesaw model. How
-
ever, the effective number of relativistic degrees of freedom is now double
d
(
i.e.
,
g
∗
= 228
.
75 as compare
d
wit
h
g
∗
=
106
.
7
5 in the SM-like case
)
,leadin
g
to a dilution factor of two for the
N
i
NN
-
induced
(
or
˜
N
i
NN
-induced
)
lepton num-
b
er asymmetry. In t
h
e strong was
h
out regime t
h
e inverse
d
ecays
d
ou
bl
et
he
was
h
out rates an
dh
ence t
h
e tota
ll
epton num
b
er as
y
mmetr
y
is suppresse
dby
a
nother factor of two.
A
ll in all, the final bar
y
on number as
y
mmetr
y
is more
or
l
ess t
h
e same in a supersymmetric seesaw mo
d
e
l
as t
h
at in a conventiona
l
s
eesaw scenario
(
Davidson
et al
., 2008
)
.
I
t has been shown that new sources of CP violation ma
y
exist in a super
-
s
ymmetric seesaw model: indirect CP violation is possible to arise from th
e
m
ixin
gb
etween
˜
N
i
N
N
a
n
d
˜
N
∗
i
NN
and in the inter
f
erence o
f
deca
y
swithandwith-
out mixing
(
Grossma
n
e
tal
.
,
2003
;
D’Ambrosi
o
e
tal.
,
2003
)
. For illustration
,
we consi
d
er a one-
g
eneration toy mo
d
e
l
w
h
ose superpotentia
l
rea
d
s
W
=
Y
LNH
u
+
1
2
M
NN
,
(
11.105
)

414 11 Cosmological Matter-antimatter Asymmetr
y
whe
r
e
N
,
L
a
n
d
H
u
stand
f
or the sin
g
let neutrino, lepton doublet and up
-
type Hi
gg
s doublet chiral superfields, respectively. Note that
Y
i
stheYukawa
c
oup
l
ing constant, an
d
M
is the Majorana mass of the neutrino singlet. Th
e
s
upersymmetry-
b
rea
k
in
g
terms invo
l
vin
g
t
h
esin
gl
et sneutrino ar
e
−L
sof
t
=˜
m
2
˜
N
∗
˜
N
+
AY
˜
H
˜
N
+
1
2
BM
˜
N
˜
N
+h
.
c
.
,
(
11.106
)
where ˜
m
2
is the soft mass of the sneutrino
,
A
a
nd
B
d
enote the trilinear an
d
bilinear scalar couplings. So the heavy Majorana neutrino has a mass
M
,
a
n
dthes
n
eut
rin
o
˜
N
m
ix
es w
i
th the a
n
t
i-
s
n
eut
rin
o
˜
N
∗
v
i
athe
m
ass
m
at
rix
which can directly be read off from Eqs.
(
11.105
)
and
(
11.106
)
. In the basis
Φ
≡
(
˜
N
∗
,
˜
N
)
T
,
we write out the mass term as follows:
−
L
m
=
1
2
Φ
†
M
2
Φ
=
1
2
˜
N
˜
N
∗
M
2
+˜
m
2
BM
B
∗
MM
2
+˜
m
2
˜
N
∗
˜
N
.
(
11.107
)
In analogy with the
K
0
-
K
0
mixing system, the evolution of the
˜
N
-
˜
N
∗
m
ix
-
i
n
g
system is
g
overned by the e
ff
ective Hamiltonia
n
H
=
$
M
−
i
3
Γ
/
2
,w
h
ere
H
ermitian
$
M
an
d
3
Γ
c
an be expressed as
(
D’Ambrosi
o
e
tal
.
,
2003
)
$
M
=
M
1
B/
(
2
M
)
B
/
(
2
M
)
1
,
3
Γ
=
Γ
1
A
∗
/M
A/M
1
(
11.108
)
to the lowest order of the soft terms. Note that the total deca
y
rate o
f
˜
N
i
sgiven
by
Γ
=
Y
2
M
/
(4
π
)
. Note also that we have chosen a specific phase
c
onventioninw
h
ic
h
on
ly
A
i
s complex. The ei
g
enstates o
f
H
a
r
edefi
n
ed as
˜
N
L
NN
=
p
˜
N
+
q
˜
N
∗
,
˜
N
H
NN
=
p
˜
N
−
q
˜
N
∗
,
(
11.109
)
where the subscript “L”
(
or “H”
)
means “light”
(
or “heavy”
),
p
a
n
d
q
a
r
e
the mixin
g
parameters which are commonly used in the phenomenolo
g
yo
f
n
eutral meson-antimeson mixing and CP violation
(
Xing, 1997
)
. The proper-
time evolution of the initial sneutrino states
|
˜
N
an
d
|
˜
N
∗
rea
ds
|
˜
N
(
t
)
=
g
+
(
t
)
|
˜
N
+
q
p
g
−
(
t
)
|
˜
N
∗
,
|
˜
N
∗
(
t
)
=
g
+
(
t
)
|
˜
N
∗
+
p
q
g
−
(
t
)
|
˜
N
,
(
11.110
)
where
g
+
(
t
)
=ex
p
−
i
M
+
Γ
2
cosh
i
Δ
M
−
Δ
Γ
2
t
2
,
g
−
(
t
)
=ex
p
−
i
M
+
Γ
2
sin
h
i
Δ
M
−
Δ
Γ
2
t
2
,
(
11.111
)
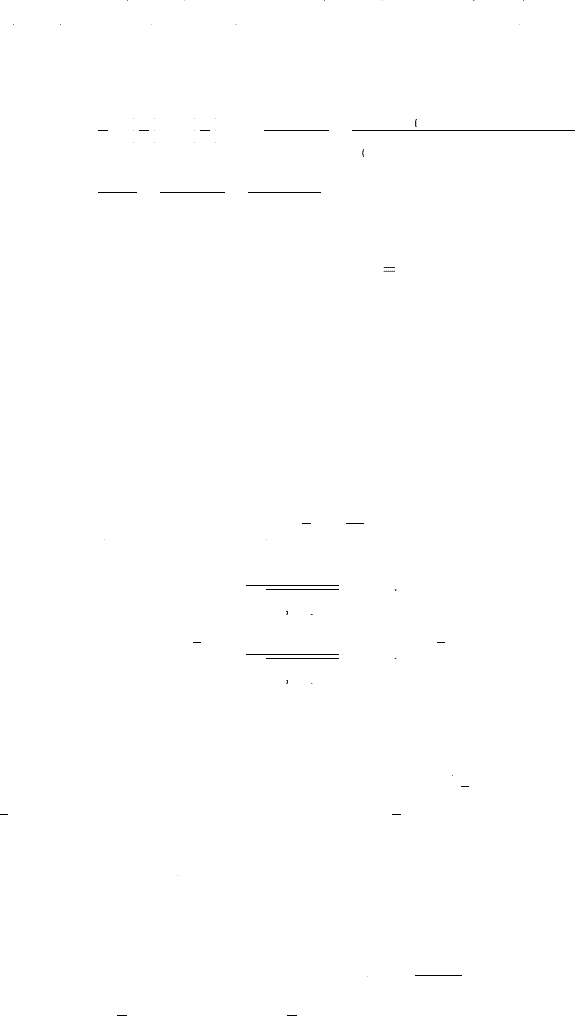
1
1.4 Recent Deve
l
opments in Leptogenesis 41
5
w
i
th
M
=(
M
L
MM
+
M
H
MM
)
/
2
,
Δ
M
≡
M
H
MM
−
M
L
MM
,
Γ
≡
(
Γ
L
ΓΓ
+
Γ
H
ΓΓ
)
/
2
a
n
d
Δ
Γ
≡
Γ
L
Γ
Γ
−
Γ
H
Γ
Γ
.
Here
M
L
M
M
,
H
an
d
Γ
L
Γ
Γ
,
H
a
rethemassandwidthof
˜
N
L
N
N
,
H
,
respectivel
y
.
The time-integrated CP-violating asymmetry, defined in the standard way
(
Xing, 1997
)
, turns out to be
(
D’Ambrosi
o
et al.
,
2003
)
ε
=
1
2
q
p
2
−
p
q
2
c
B
−
c
F
c
B
+
c
F
7
∞
0
77
d
t
|
g
−
(
t
)
|
2
7
∞
0
77
d
t
(
|
g
−
(
t
)
|
2
+
|
g
+
(
t
)
|
2
)
≈
Im
A
M
c
B
−
c
F
c
B
+
c
F
ΓB
Γ
2
+
B
2
,
(
11.112
)
where c
B
an
d
c
F
p
arametrize the
p
hase-s
p
ace contributions of the bosoni
c
a
n
d
f
e
rmi
o
ni
c
fin
a
l
states
.N
ote t
h
at
|
q
/p
|
=
1imp
l
ies t
h
e mixing-in
d
uce
d
C
P violation. This so
f
tlepto
g
enesis mechanism may even o
ff
er the dominan
t
s
ource of CP violation to produce the observed bar
y
on number as
y
mmetr
y
of the Universe
(
Grossma
n
et al
., 2003; D’Ambrosi
o
et al
., 2003
).
11.4.4 Flavor Effects
So far we have assumed that the Yukawa interactions of charged leptons
a
re ne
g
li
g
ible in lepto
g
enesis, and thus there are no interactions which ca
n
d
istinguish one lepton flavor from another. In this case it is convenient to
d
e
fi
ne the lepton and antilepton states
f
rom the decays o
f
heavy Majorana
neut
r
i
n
os
N
i
NN
→
α
+
H
a
n
d
N
i
NN
→
α
+
H
:
|
i
≡
1
(
Y
†
ν
YY
Y
ν
YY
)
ii
α
(
Y
ν
YY
)
αi
|
α
,
|
i
≡
1
(
Y
†
ν
Y
Y
Y
ν
YY
)
ii
α
(
Y
∗
ν
YY
)
αi
|
α
,
(
11.113
)
w
h
ic
h
are a
l
so t
h
e states invo
l
ve
d
in t
h
esu
b
sequent inverse
d
ecays an
d
scat
-
terin
g
processes. However, the Yukawa interactions o
f
char
g
ed leptons ar
e
possible to be faster than the
(
inverse
)
decays o
f
N
i
N
N
a
nd destroy the coher-
ent absorption or scatterin
g
of the states
|
i
an
d
|
i
.
Note tha
t
|
i
a
nd
i
are not
C
P-conju
g
ate states, althou
gh
|
α
i
tsel
f
is the
C
P conju
g
ate
of
|
α
.
Let us estimate the interactions involving the tau leptons, such a
s
τ
L
+
Q
3L
→
t
R
+
τ
R
ττ
w
i
th
Q
3L
=(
t
L
,b
L
)
T
a
n
d
τ
L
=(
ν
τ
L
,τ
L
ττ
)
T
b
eing t
he
third-
f
amily quark and lepton doublets. Ne
g
lectin
g
all the relevant masses,
one may immediately obtain the cross section
(
Davidson et al., 2008
)
σ
(
τ
L
+
Q
3
L
→
t
R
+
τ
R
τ
τ
)=
y
2
t
y
2
τ
16
π
s
,
(
11.114
)
w
h
e
r
e
y
t
=
√
2
m
t
/v
a
n
d
y
τ
=
√
2
m
τ
/
v. With the help of Eq.
(
11.114
)
,one
c
an further compute the corresponding interaction rate density γ
τ
introduce
d
