Xing Zh., Zhou Sh. Neutrinos in Particle Physics, Astronomy and Cosmology
Подождите немного. Документ загружается.


396 11 Cosmological Matter-antimatter Asymmetr
y
d
β
N
j
N
H
c
N
i
N
N
a
α
H
b
N
i
NN
d
β
H
b
N
j
N
a
α
H
c
(
b)(a
)
Fi
g
. 11.5 The Feynman dia
g
rams
f
or the one-loop vertex corrections to the decays
o
f
heav
y
Ma
j
orana neutrinos
N
i
NN
:
(
a
)
N
i
N
N
→
α
+
H
a
nd
(
b
)
N
i
NN
→
α
+
H
,
w
h
ere
the arc arrows denote the direction of the fermion flow (Denner
et al.
, 1992. With
permission from Elsevier
)
i
Γ
a
b
αi
Γ
Γ
=
β
c,
d
j
−
i
(
Y
ν
YY
)
αj
ac
−
i(
Y
T
ν
YY
)
jβ
(
T
)
bd
−
i
(
Y
∗
ν
YY
)
β
i
d
c
×
d
4
k
(
2
π
)
4
P
R
PP
[i
S
(
/
p
//
+
/
k
//
+
/
p
//
,M
j
M
)]
P
R
PP
[
i
S
(
/
p
//
+
/
k
//
)]
P
L
PP
[
iΔ
(
k
2
)]
,
(
11.47
)
whe
r
e
i
S
(
/
p, M
//
j
M
)
is the propagator of
N
j
N
,
i
S
(
/
p
//
)
denotes the propagator of th
e
l
epton doublet in the neglect of lepton masses, and i
Δ
(
k
2
)
represents th
e
propagator of massless scalars. Using the dimensional regularization method
,
we explicitl
y
work out this e
ff
ective vertex
:
Γ
ab
αi
ΓΓ
=
j
a
b
(
Y
ν
Y
Y
)
αj
$
M
B
K
T
ji
/
p
//
+
$
M
C
K
T
ji
/
p
//
P
L
P
P
,
(
11.48
)
w
h
ere
$
M
,
B
an
d
C
a
re t
h
ree
d
iagona
l
matrices:
$
M
=D
ia
g
{
M
1
,M
2
MM
,M
3
MM
}
,
an
d
the dia
g
onal elements o
f
B
a
n
d
C
are
(
fo
r
k
=
1
,
2
,
3
)
B
k
(
p
2
,
p
2
)
=
1
16
π
2
[
C
1
1
(
p
,
p
,
0
,
0
,M
k
M
)
+
C
0
CC
(
p
,
p
,
0
,
0
,M
k
M
)]
,
C
k
(
p
2
,
p
2
)
=
1
16
π
2
C
1
2
(
p
,
p
,
0
,
0
,M
k
M
)
(
11.49
)
w
i
th
C
0
C
C
,
C
1
1
a
n
d
C
12
b
ein
g
the three-point Passarino-Veltman
f
unctions
(
Denner, 1993
)
. The Feynman diagram for the one-loop vertex corrections
to the CP-conjugate decay
N
i
NN
→
α
+
H
is shown Fig. 11.5
(
b
)
. Its effective
vertex is simi
l
ar
ly
expresse
d
as
Γ
ab
α
i
=
j
a
b
(
Y
∗
ν
Y
Y
)
α
j
$
M
B
K
ji
/
p
/
/
+
$
M
C
K
ji
/
p
/
/
P
R
PP
,
(
11.50
)
whe
r
e
B
a
n
d
C
have been given in Eq.
(
11.49
)
. After a sum of the contribution
s
f
rom Fig. 11.3
(
a
)
and Fig. 11.3
(
c
)
, the overall decay amplitude o
f
N
i
N
N
→
α
+
H
with the one-loo
p
vertex corrections is then obtained:

1
1.3
B
aryogenesis via
L
eptogenesis 39
7
i
M
v
,
a
b
αi
=
−
i
u
(
q
)
(
Y
ν
YY
)
α
i
ab
P
R
PP
−
Γ
a
b
αi
Γ
Γ
u
(
p
)
.
(
11.51
)
The overall deca
y
amplitude o
f
N
i
NN
→
α
+
H
is similarly
g
iven by
i
M
v
,ab
αi
=
−
i
v
(
q
)
(
Y
∗
ν
YY
)
αi
a
b
P
R
PP
−
Γ
ab
α
i
u
(
p
)
.
(
11.52
)
Integratin
g
|M
v
,
a
b
α
i
|
2
an
d
|
M
v
,a
b
αi
|
2
o
ver the
p
hase s
p
ace of final states, we
a
rrive at the CP-violating asymmetries induced by the vertex corrections
:
ε
v
iα
=
1
2
M
i
MM
d
Π
q
Π
d
Π
k
(2
π
)
4
δ
4
(
p
−
q
−
k
)
a
,
b
M
v
,
a
b
αi
2
−
M
v
,
ab
αi
2
α
Γ
(
N
i
NN
→
α
+
H
)+
Γ
(
N
i
NN
→
α
+
H
)
=
1
8
π
K
ii
K
j
Im
(
Y
∗
ν
YY
)
α
i
(
Y
ν
YY
)
α
j
K
ij
K
f
v
ff
M
2
j
M
M
2
i
M
,
(
11.53
)
where the vertex functio
n
f
v
ff
(
M
2
j
M
/M
2
i
MM
)
is defined by
f
v
ff
(
x
)
≡
√
x
1
+
(
1+
x
)
ln
x
1
+
x
.
(
11.54
)
N
ote t
h
at t
h
etermwit
h
j
=
i
o
n the right-hand side of Eq.
(
11.53
)
is actu
-
a
lly vanishin
g
. In the leadin
g
-order approximation the overall
C
P-violatin
g
a
s
y
mme
t
r
y
ε
iα
is simply a sum of the CP-violating asymmetries induced by
vertex and self-energy corrections
(
i.e.
,
ε
iα
=
ε
v
i
α
+
ε
s
iα
)
. Taking account o
f
E
qs.
(
11.45
)
and
(
11.53
)
, we obtain
ε
iα
=
1
8
π
(
Y
†
ν
YY
Y
ν
YY
)
ii
j
=
i
2
Im
(
Y
∗
ν
YY
)
αi
(
Y
ν
YY
)
αj
(
Y
†
ν
YY
Y
ν
YY
)
ij
F
M
2
j
M
M
2
i
MM
+
I
m
(
Y
∗
ν
YY
)
α
i
(
Y
ν
YY
)
α
j
(
Y
†
ν
YY
Y
ν
YY
)
∗
ij
G
M
2
j
M
M
2
i
M
6
,
(
11.55
)
where we have introduced the loop
f
unction
s
G
(
x
)
≡
1
/
(
1 −
x
)
and
F
(
x
)=
√
x
1+
1
1
−
x
+
(
1
+
x
)
l
n
x
1
+
x
.
(
11.56
)
If all the interactions in the era of leptogenesis were blind to lepton flavors,
then only the total
C
P-violatin
g
asymmetr
y
ε
i
should be
r
eleva
n
t:
ε
i
=
α
ε
iα
=
1
8
π
(
Y
†
ν
Y
Y
Y
ν
YY
)
i
i
j
=
i
Im
(
Y
†
ν
Y
Y
Y
ν
Y
Y
)
2
ij
F
M
2
j
M
M
2
i
M
M
.
(
11.57
)

398 11 Cosmological Matter-antimatter Asymmetr
y
The above results are ver
y
use
f
ul
f
or the stud
y
o
ffl
avor-dependent and
fl
avor-
i
ndependent lepto
g
enesis scenarios in the type-I seesaw models.
T
he lepton number asymmetries can be generated from the CP-violating
a
nd out-o
f
-equilibrium deca
y
so
f
heav
y
Ma
j
orana neutrino
s
N
i
N
N
. Naive
ly
,a
d
ifference between the number densities of leptons
(
n
)
and antileptons
(
n
)
i
s determined by the CP-violating asymmetr
y
ε
i
and the number density of
h
eav
y
Ma
j
orana neutrinos
n
N
i
;i
.e.
,
n
−
n
∝
ε
i
n
N
i
.
B
ut
n
N
i
m
ay c
h
an
g
e
due to the decay and inverse-decay processes. The values of
ii
i
n
a
nd
n
may
a
lso be modified by both the decays and lepton-number-violating scatterin
g
processes. Hence an exact calculation o
f
the lepton and bar
y
on number as
y
m
-
m
etries relies on the solution to the full set of Boltzmann equations
(
Kolb
a
n
d
Turner, 1990; Luty, 1992; P
l
¨umac
h
er, 1997; Davi
d
so
n
et al
., 2008
).
11.3.3 Boltzmann E
q
uation
s
The Boltzmann equations are widely regarded as the standard tools for de
-
termining the particle number densities which may more or less be modifie
d
by decays and collisions in the expanding Universe
(
Kolb and Turner, 1990
)
.
Given the large mass scale of heavy Majorana neutrinos, the leptogenesis
m
ec
h
anism must
h
ave wor
k
e
d
in t
h
everyear
l
yUniversew
h
ere t
h
e tota
l
en
-
er
g
y density was dominated by relativistic particles and all the
S
M particles
were in thermal equilibrium. To be specific, the number density of the
“
x
”
partic
l
es in t
h
erma
l
equi
l
i
b
rium at t
h
e temperature
T
i
s
d
escri
b
e
db
y
n
x
=
g
x
d
3
p
(2
π
)
3
f
x
ff
(
p
)=
g
x
d
3
p
(2
π
)
3
1
exp
[(
E
x
−
μ
x
)
/T
]
±
1
,
(
11.58
)
where
g
x
represents the number of internal degrees of freedom,
f
x
f
f
(
p
)
is the
d
istribution
f
unction in the phase space
,
m
x
de
n
otes t
h
e
m
ass of t
h
e
“
x
”
p
article
,
T
m
x
a
nd
E
x
=
|
p
|
2
+
m
2
x
→
|
p
|
hold
,
μ
x
s
tands for th
e
ch
emica
l
potentia
l
,an
d
t
h
e
“
±
”
signs correspond to fermions
(
+
)
and boson
s
(
−
)
. Neglecting the tiny chemical potentials, one may calculate the energy
d
ensities of relativistic bosons and fermions
(
see Section 9.1.4
):
ρ
=
g
∗
π
2
30
T
4
,
(
11.59
)
w
h
e
r
e
g
∗
i
sthee
ff
ective number o
f
de
g
rees o
ff
reedom and its expression ha
s
been given in Eq.
(
9.29
)
. In the SM of electroweak and strong interaction
s
g
∗
= 106
.
7
5
h
o
ld
sw
h
en t
h
e temperature is muc
hh
i
gh
er t
h
an t
h
ee
l
ectrowea
k
g
au
g
e symmetry breakin
g
scale
v
≈
2
46 Ge
V
5
. The Hubble
p
arameter
H
5
At
T
∼
v
th
eHi
gg
s
b
oson, t
h
ep
h
oton an
d
t
h
ree massive
g
au
g
e
b
osons tota
ll
y
contribute 1
+
2
+3
×
3
=12to
g
∗
.
A
t
T
v
,
however, the electroweak gauge
symmetry is restored and all the gauge bosons are massless. In this case four real
components o
f
the Hi
gg
s doublet and two polarization states o
f
each
g
au
g
e boson
should be taken into account. So they also contribute 4 + 2
×
4
=12t
o
g
∗
.

1
1.3
B
aryogenesis via
L
eptogenesis 39
9
i
nt
h
is ra
d
iation-
d
ominate
d
epoc
h
can
b
e expresse
d
as
H
≈
1
.
66
√
g
√√
∗
T
2
/M
Pl
MM
wit
h
M
Pl
M
M
b
eing the Planck mass, as already shown in Eq.
(
9.31
)
. The entropy
d
ensity of the Universe is defined as
s
≡
ρ
+
p
T
=
4
ρ
3
T
=
2˜
g
∗
π
2
45
T
3
,
(
11.60
)
where the e
q
uation of stat
e
p
=
ρ/
3
is used for the relativistic gas, an
d
˜
g
∗
≡
b
g
b
T
∗
b
TT
T
3
+
7
8
f
g
f
T
∗
f
TT
T
3
(
11.61
)
d
enotes the e
ff
ective number o
f
de
g
rees o
ff
reedom
f
or the entropy wit
h
T
∗
b
TT
a
n
d
T
∗
f
T
T
b
ein
g
the decouplin
g
temperatures o
f
the correspondin
g
bosons and
f
ermions. Since all the
p
articles should be in thermal e
q
uilibrium at the tem-
peratur
e
T
M
i
MM
,w
h
er
e
M
i
MM
are the masses o
f
heavy Majorana neutrinos
N
i
NN
,
we have
T
∗
b
TT
=
T
∗
f
TT
=
T
and therefore ˜
g
∗
=
g
∗
as given in Eq.
(
9.29
)
.Whe
n
T<M
i
M
M
,h
owever
,
non-re
l
ativistic
N
i
NN
must
h
ave
d
ecaye
d
an
d
t
h
eir num
b
er
d
ensities in thermal equilibrium are suppressed b
y
the Boltzmann
f
actors
e
−
M
i
/
T
. To illustrate how a simple lepto
g
enesis mechanism works, here we
only consider the role of the lightest heavy Majorana neutrin
o
N
1
N
N
an
d
assum
e
that the lepton number as
y
mmetries produced previousl
yf
rom the deca
y
so
f
N
2
N
N
a
nd
N
3
NN
h
ave been completel
y
washed out
6
. Furthermore, we neglect th
e
Yukawa interactions of charged leptons and focus on the flavor-independent
C
P-violatin
g
asymmetrie
s
ε
i
o
btained in Eq.
(
11.57
).
Now we
p
resent an intuitive derivation of the Boltzmann e
q
uations in the
expanding Universe. The number density of the “
a
”
particles is defined a
s
n
a
≡
N
a
N
/
V ,wher
e
N
a
N
i
st
h
e tota
ln
u
m
be
r
of t
h
e“
a
” particles in the ph
y
sical
volum
e
V
=
V
0
VV
R
3
(
t
)
/R
3
(
t
0
)
wit
h
V
0
VV
b
eing the volume in the comoving co
-
ordinate system. In the absence o
f
any interactions
N
a
N
sh
ou
ld b
e conserve
d
;
i
.e.,
˙
N
a
N
=
0 or equivalentl
y
d
(
n
a
V
)
d
t
=
V
(˙
n
a
+3
Hn
a
)
=
0
,
(
11.62
)
where
H
=
˙
R
(
t
)
/
R
(
t
)
is the Hubble parameter. If there exist collisions whic
h
ch
ang
e
n
a
,
they should contribute to the right-hand side of Eq.
(
11.62
)
.Fo
r
i
nstance, t
h
e reaction
a
+
X
→
Y
a
n
d
its inverse proces
s
Y
→
a
+
X
can
m
odif
y
the number of the
“
a
”
particles by one unit. Hence the change of th
e
partic
l
enum
b
er in t
h
ep
h
ysica
l
vo
l
um
e
V
in
the u
ni
tt
im
eca
n
be w
ri
tte
n
as
−
V
X
,
Y
d
Π
a
Π
d
Π
X
Π
d
Π
Y
ΠΠ
(2
π
)
4
δ
4
(
p
a
+
p
X
−
p
Y
)
{
f
a
f
f
f
X
f
(1
±
f
Y
ff
)
6
T
he contributions of heavier Majorana neutrino
s
N
2
N
N
a
n
d
N
3
N
N
to t
h
e
l
epto
n
number asymmetries should in
g
eneral be included, and the washout e
ff
ects on
these asymmetries can be evaluated by solving the relevant Boltzmann equations.

400 11 Cosmological Matter-antimatter Asymmetr
y
×
|M
(
a
+
X
→
Y
)
|
2
−
f
Y
ff
(1
±
f
a
ff
)(
1
±
f
Y
f
f
)
|M
(
Y
→
a
+
X
)
|
2
,
(
11.63
)
where
M
(
a
+
X
→
Y
)
and
M
(
Y
→
a
+
X
)
are the Feynman amplitudes. Note
that the amplitudes should be summed over all the internal degrees of freedo
m
o
f
initial and
fi
nal states. Two reasonable approximations are usuall
y
made to
s
implify the collision integral:
(
a
)
the Maxwell-Boltzmann distribution func-
tio
n
f
x
ff
=
n
x
e
−
E
/T
/
n
eq
x
=
e
−
(
E
−
μ
x
)
/
T
i
sta
k
en
,
w
h
er
e
n
eq
x
=
g
x
7
d
Π
x
Π
e
−
E/
T
s
tands for the number density in thermal equilibrium; and
(
b
)
1
±
f
x
ff
≈
1
h
olds due t
o
f
x
f
f
≈
e
−
E
/T
≈
0
.
05
,
wher
e
E
=
3
T
is the average energy.
Then the Boltzmann equation can be derived from Eqs.
(
11.62
)
and
(
11.63
)
(
Kolb and Turner, 1990; Luty, 1992
)
. After a straightforward calculation, w
e
a
rr
i
ve a
t
˙
n
a
+
3
Hn
a
=
X
,
Y
n
Y
n
e
q
Y
γ
(
Y
→
a
+
X
)
−
n
a
n
eq
a
·
n
X
n
eq
X
γ
(
a
+
X
→
Y
)
,
(
11.64
)
where the interaction rate density is defined as
γ
(
a
+
X
→
Y
)
≡
d
Π
a
Π
d
Π
X
Π
d
Π
Y
ΠΠ
(2
π
)
4
δ
4
(
p
a
+
p
X
−
p
Y
)
×
e
−
E
a
/
T
e
−
E
X
/
T
|M
(
a
+
X
→
Y
)
|
2
.
(
11.65
)
It is more convenient to express the Boltzmann equation in terms o
f
th
e
particle number per unit entrop
y
Y
a
YY
≡
n
a
/s
and to re
p
lace the time
t
w
i
th
t
h
e
d
imension
l
ess varia
bl
e
z
≡
M
a
M
/
T . Note t
h
a
t
d
Y
a
YY
d
z
=
d
t
d
z
·
d
d
t
V
n
a
V
s
=
d
t
d
z
·
˙
n
a
+3
Hn
a
s
(
11.66
)
h
o
ld
s, w
h
ere t
h
e tota
l
entropy
Vs
i
s conserve
d
. Becaus
e
H
(
t
)
=
1
/
(2
t
)
and
T
∝
1
/
√
t
i
nt
h
era
d
iation-
d
ominate
d
epoc
h
,itiseasytos
h
o
w
d
t
d
z
=
1
/
(
H
z
)
.
A
s a direct result, the Boltzmann equation in Eq.
(
11.64
)
can be rewritte
n
as
d
Y
a
YY
d
z
=
1
s
Hz
X,Y
Y
Y
YY
Y
eq
Y
YY
γ
(
Y
→
a
+
X
)
−
Y
a
YY
Y
e
q
a
YY
·
Y
X
YY
Y
e
q
X
YY
γ
(
a
+
X
→
Y
)
.
(
11.67
)
The evolution of the number density of the heavy Majorana neutrino
N
1
NN
a
nd
that o
f
the lepton number asymmetry produced
f
ro
m
N
1
NN
d
ecays are
g
overne
d
by the correspondin
g
Boltzmann equations. The latter can be
fi
xed a
f
ter a
c
alculation of the interaction rate densities of the decays and lepton-number
-
vio
l
atin
g
scatterin
g
processes.
W
e first consider the lepton-number-violatin
g
decay
s
N
i
N
N
→
α
+
H
a
nd
N
i
N
N
→
α
+
H
t
oget
h
er wit
h
t
h
eir inverse processes
α
+
H
→
N
i
N
N
a
n
d
α
+
H
→
N
i
NN
.Therateso
f
these reactions have been
g
iven in
S
ection 11.3.2. The

1
1.3
B
aryogenesis via
L
eptogenesis 40
1
c
orrespondin
g
reaction rate density o
f
N
i
NN
→
α
+
H
ca
n
be calculated w
i
th
the help of Eq.
(
11.65
)
:
γ
(
N
i
NN
→
α
H
)
=
d
Π
N
i
e
−
E
N
i
/T
d
Π
Π
α
d
Π
H
×
(2
π
)
4
δ
4
(
p
N
i
−
p
α
−
p
H
)
|M
(
N
i
NN
→
α
+
H
)
|
2
=
g
N
i
d
Π
N
Π
i
e
−
E
N
i
/T
2
M
i
M
M
Γ
(
N
i
NN
→
α
+
H
)
=
n
e
q
N
i
K
1
(
z
)
K
2
(
z
)
Γ
(
N
i
NN
→
α
+
H
)
,
(
11.68
)
whe
r
e
Γ
(
N
i
NN
→
α
+
H
)
denotes the partial decay width o
f
N
i
NN
→
α
+
H
in
the rest frame of
N
i
NN
,
and
K
1
(
z
)
≡
z
−
1
+
∞
z
e
−
y
y
2
−
z
2
d
y,
K
2
(
z
)
≡
z
−
2
+
∞
z
y
e
−
y
y
2
−
z
2
d
y
(
11.69
)
a
re the modified Bessel functions
(
Kolb and Turner, 1990
)
. Concentratin
g
on t
h
e
l
ig
h
test
h
eavy Majorana neutrin
o
N
1
NN
an
d
summing over t
h
e
l
epton
fl
avors, we obtain the total deca
y
rate densit
y
γ
D
=
α
γ
(
N
1
NN
→
α
+
H
)
+
γ
(
N
1
NN
→
α
+
H
)
=
n
e
q
N
i
K
1
(
z
)
K
2
(
z
)
Γ
1
ΓΓ
,
(
11.70
)
w
h
ere
Γ
1
ΓΓ
has been given in Eq.
(
11.36
)
. When the one-loop corrections to
Γ
(
N
1
NN
→
+
H
)
an
d
Γ
(
N
1
NN
→
+
H
)
are taken into account, their difference
becomes nonzero and is characterized by the CP-violatin
g
asymmetr
y
ε
1
given in Eq.
(
11.57
)
. The CPT symmetry leads us t
o
γ
(
N
1
NN
→
+
H
)
=
γ
(
+
H
→
N
1
NN
)=
1
2
(
1
+
ε
1
)
γ
D
,
γ
(
N
1
NN
→
+
H
)
=
γ
(
+
H
→
N
1
NN
)=
1
2
(1
−
ε
1
)
γ
D
.
(
11.71
)
The important scattering processes include
(
a
)
the lepton-number-violating
Δ
L
=
1 processes involvin
g
the up-type quarks
:
N
i
NN
+
α
→
Q
+
U
,
N
i
NN
+
Q
→
α
+
U
an
d
N
i
NN
+
U
→
α
+
Q
(
Fig. 11.6
)
, where the dominant contributions ar
e
i
nduced by the top quark;
(
b
)
the
Δ
L
=
1 processes invo
l
vin
g
t
h
ee
l
ectrowea
k
g
au
g
e bosons:
N
i
NN
+
α
→
H
+
V
μ
VV
,
N
i
NN
+
α
→
V
μ
VV
+
H
an
d
N
i
NN
+
H
→
α
+
V
μ
VV
(
Fig. 11.7
)
,wher
e
V
μ
V
V
sta
n
ds
f
o
r
W
i
μ
W
(
for
i
=
1
,
2
,
3)
an
d
B
μ
;
(
c
)
th
e
Δ
L
=
2
processes:
α
+
H
→
β
+
H
a
n
d
α
+
β
→
H
+
H
(
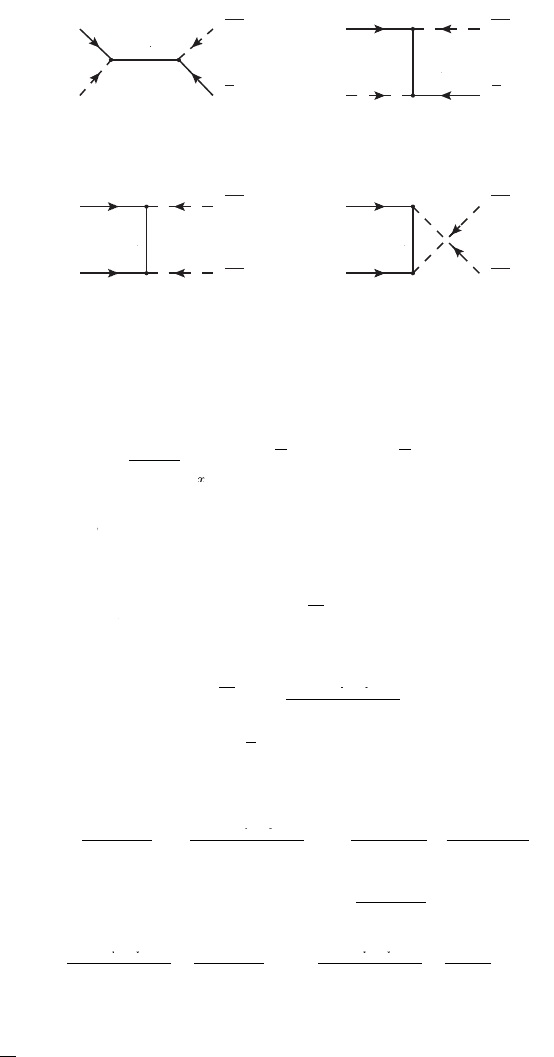
Fig. 11.8
)
. In general, on
e
m
a
y
de
fi
ne the reduced cross section
f
or the proces
s
a
+
X
→
Y
as fo
ll
ows
(
Davidson et al., 2008
)
:
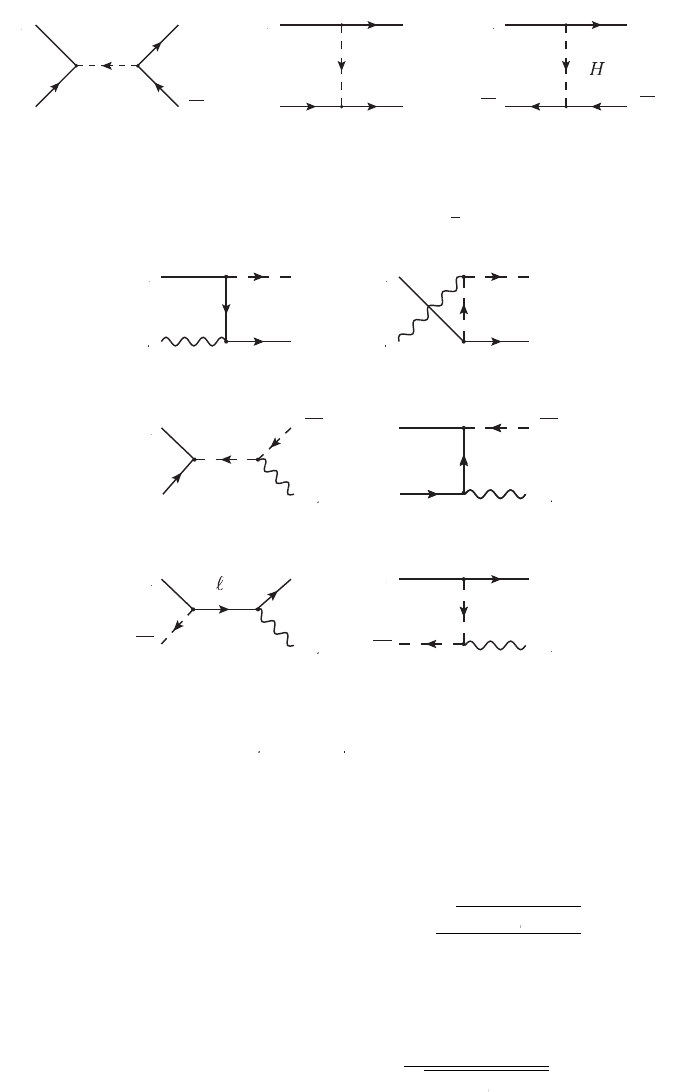
402 11 Cosmological Matter-antimatter Asymmetr
y
H
H
N
i
NN
U
Q
α
Q
U
α
N
i
NN
N
i
NN
α
Q
U
(
a
)(
b
)
(
c
)
Fig. 11.6 The Feynman diagrams
f
or th
e
Δ
L
=
1 scattering processes invo
l
ving
t
h
e top quar
k
,w
h
ose Yu
k
awa coup
l
in
g
constan
t
y
t
=
√
2
m
t
/v
is o
f
O
(
1
)
N
i
NN
H
α
V
μ
VV
N
i
NN
V
μ
VV
α
H
H
(
b)
α
N
i
NN
H
(a
)
H
H
α
N
i
NN
α
α
V
μ
VV
V
μ
VV
(
d)
(c)
N
i
NN
V
μ
VV
α
α
H
(
e)
N
i
NN
H
H
α
V
μ
VV
(
f
)
Fig. 11.7 The Feynman diagrams
f
or th
e
Δ
L
=
1 scattering processes invo
l
ving
t
h
ee
l
ectrowea
kg
au
g
e
b
osons
V
μ
VV
,
w
h
er
e
V
μ
VV
=
W
i
μ
W
a
n
d
B
μ
(
fo
r
i
=1
,
2
,
3)
ˆ
σ
(
s
)
≡
8
π
Φ
2
(
s
)
d
Π
Y
Π
Π
(
2
π
)
4
δ
4
(
p
a
+
p
X
−
p
Y
)
|
M
(
a
+
X
→
Y
)
|
2
,
(
11.72
)
where
Φ
2
(
s
)
is the two-particle phase space integration
Φ
2
(
s
)
≡
d
Π
a
Π
d
Π
X
Π
(
2
π
)
4
δ
4
(
p
a
+
p
X
−
q
)=
λ
(
s
,M
2
a
M
,M
2
X
M
)
8
π
s
(
11.73
)
wit
h
s
=
q
2
an
d
λ
(
x
,
y
,
z
)
≡
(
x
−
y
−
z
)
2
−
4
y
z
.
Now Eq.
(
11.65
)
can be
recast into the following form
(
Giudic
e
et a
l
., 2004
)
:
γ
(
a
+
X
→
Y
)
=
d
Π
a
Π
d
Π
X
Π
e
−
E
a
/
T
e
−
E
X
/
T
s
λ
(
s
,M
2
a
M
,M
2
X
M
)
ˆ
σ
(
s
)
1
1.3
B
aryogenesis via
L
eptogenesis 40
3
H
H
H
H
α
N
i
N
N
N
i
NN
α
H
H
H
H
N
i
NN
α
β
α
(
a
)
(
b
)
(c
)
(
d
)
β
β
β
N
i
NN
Fi
g
. 11.8 The Feynman dia
g
rams
f
or the
Δ
L
= 2 scatterin
g
processes, an
d
t
h
e
on-shell contributions in the
s
-
channel dia
g
ram should be subtracted for consistency
=
M
4
a
M
6
4
π
4
z
∞
x
th
r
d
x
√
x
ˆ
σ
(
x
)
K
1
(
z
√
x
)
,
(
11.74
)
w
h
e
r
e
x
≡
s
/M
2
a
M
,
an
d
x
th
r
i
s the threshold value
f
or the
p
roces
s
a
+
X
→
Y
to
take place. Note that we have inserted the identit
y
7
δ
4
(
p
a
+
p
X
−
q
)
d
4
q
=1
i
nto the first line of Eq.
(
11.74
)
and changed the order of integration. T
o
i
llustrate, we ma
y
explicitl
y
work out the reduced cross section
f
or th
e
s
-
c
hannel
p
roces
s
N
1
NN
(
p
)
+
(
p
)
→
Q
(
k
)+
U
(
k
)
in Fig. 11.6
(
a
)
.Ifonlytheto
p
q
uar
k
contri
b
ution is consi
d
ere
d
,weo
b
tain
|M
(
N
1
N
N
+
→
Q
+
U
)
|
2
=
8
y
2
t
Y
†
ν
YY
Y
ν
YY
1
1
s
2
(
p
·
p
)(
k
·
k
)
,
(
11.75
)
where
s
=(
p
+
p
)
2
a
n
d
y
t
≡
√
2
m
t
/
v wit
h
m
t
b
ein
g
the top quark mass
.
Substituting Eq.
(
11.75
)
into Eq.
(
11.72
)
, we arrive a
t
ˆ
σ
(
x
)
=
s
−
M
2
1
s
8
y
2
t
Y
†
ν
YY
Y
ν
YY
1
1
s
2
d
3
k
(
2
π
)
3
2
k
0
·
d
3
k
(2
π
)
3
2
k
0
×
(2
π
)
4
δ
4
(
p
+
p
−
k
−
k
)
s
−
M
2
1
2
(
k
·
k
)
=
y
2
t
Y
†
ν
YY
Y
ν
YY
11
4
π
s
−
M
2
1
s
2
=
y
2
t
Y
†
ν
YY
Y
ν
YY
11
4
π
x
−
1
x
2
,
(
11.76
)
whe
r
e
x
≡
s
/
M
2
1
a
n
d
p
·
p
=(
s
−
M
2
1
)
/
2 have been used. Inserting Eq.
(
11.76
)
i
nto Eq.
(
11.74
)
, one may then obtain the reaction rate densit
y
γ
(
N
1
N
N
+
→
Q
+
U
)
which appears in the Boltzmann equation. First, let us consider th
e

404 11 Cosmological Matter-antimatter Asymmetr
y
Boltzmann equation
f
or the number densit
y
o
f
heav
y
Ma
j
orana neutrino
s
(
Giudic
e
e
tal
.
,
2004
;
Buchm¨ulle
r
e
tal
.
,
2005a
)
,
s
Hz
d
Y
N
YY
1
d
z
=
−
X
,Y
[
N
1
NN
+
X
↔
Y
]
,
(
11.77
)
w
h
ere t
h
e summation s
h
ou
ld b
eta
k
en over
b
ot
h
t
h
e
d
ecays an
d
t
h
e scatter
-
i
ng processes:
(
a
)
the decays and their inverse processes
D
≡
[
N
1
NN
↔
+
H
];
(
b
)
the
Δ
L
=
1 scattering
S
s
≡
H
s
+
V
s
VV
w
it
h
H
s
≡
N
1
NN
+
↔
Q
+
U
a
n
d
V
s
VV
≡
N
1
NN
+
↔
H
+
V
μ
VV
;
(
c
)
the
Δ
L
=
1 scattering
S
t
SS
≡
H
t
HH
+
V
t
VV
with
2
H
t
HH
≡
N
1
N
N
+
Q
↔
+
U
+
N
1
NN
+
U
↔
+
Q
an
d2
V
t
VV
≡
N
1
NN
+
V
μ
VV
↔
+
H
+
N
1
N
N
+
H
↔
+
V
μ
VV
;
(
d
)
th
e
Δ
L
= 2 scatterin
g
N
s
N
≡
+
H
↔
+
H
a
n
d
N
t
N
N
≡
+
↔
H
+
H
.
Note t
h
at t
h
eterm
s
D
,S
s
,S
t
SS
and their CP-conjugat
e
t
erms
D,
S
s
,
S
t
change the number densities of bot
h
N
1
NN
and the le
p
ton dou
-
blets
a
n
d
,
w
h
i
l
et
h
eterm
s
N
s
N
,N
t
NN
a
nd their
C
P-conju
g
ate term
s
N
s
,
N
t
onl
y
modif
y
the lepton number densit
y
. Hence the Boltzmann equations for
the number densities o
f
N
1
NN
,
an
d
are given
b
y
sHz
d
Y
N
YY
1
d
z
=
−
D
−
D
−
S
s
−
S
s
−
S
t
SS
−
S
t
,
s
H
z
d
Y
YY
d
z
=
D
−
N
s
N
−
N
t
NN
−
S
s
+
S
t
,
sHz
d
Y
Y
d
z
=
D
+
N
s
N
−
N
t
−
S
s
+
S
t
SS
.
(
11.78
)
So it is strai
g
htforward to derive the Boltzmann equation for the lepton
n
um
b
er asymmetry
Y
L
YY
≡
Y
YY
−
Y
Y
=(
n
−
n
)
/s
from Eq.
(
11.78
)
.Ifonly
t
h
e
d
eca
y
san
d
t
h
eir inverse processes are ta
k
en into account, t
h
eBo
l
tzman
n
e
q
uation fo
r
Y
L
YY
t
urns out to b
e
s
H
z
d
Y
L
YY
d
z
=
D
−
D
=
ε
1
Y
N
YY
1
Y
e
q
N
Y
Y
1
+1
−
Y
L
YY
2
Y
e
q
YY
γ
D
,
(
11.79
)
where Eq.
(
11.71
)
and the identit
y
Y
YY
+
Y
Y
=2
Y
e
q
YY
have bee
n
used
.In
th
i
s
c
ase a net lepton number as
y
mmetr
y
seems to be producible even if the heav
y
Majorana neutrinos stay in thermal equilibrium
(
i.e.
,
Y
N
YY
1
=
Y
e
q
N
Y
Y
1
)
, a result i
n
c
on
fl
ict with the
g
eneral ar
g
ument that no particle number asymmetries ca
n
be
g
enerated in thermal equilibrium. The reason
f
or this paradox is that the
on-shell contributions from th
e
s
-channel
p
roces
s
+
H
↔
+
H
s
hould be
s
u
b
tracte
d
,
b
ecause t
h
ey
h
ave
b
een inc
l
u
d
e
d
in t
h
e
d
ecay an
d
inverse
d
eca
y
terms
(
Kolb and Turner, 1990; Strumia, 2006
)
. Such on-shell contribution
s
a
re estimated to b
e
γ
o
s
(
+
H
→
+
H
)
=
γ
(
+
H
→
N
1
N
N
)
Br
(
N
1
N
N
→
+
H
)
,
(
11.80
)
1
1.3
B
aryogenesis via
L
eptogenesis 40
5
where Br
(
N
1
N
N
→
+
H
)
=
(
1 −
ε
1
)
/
2
is the branchin
g
ratio o
f
N
1
N
N
→
+
H
.
A
fter a consistent subtraction
,
the reaction rate densities read
γ
(
+
H
→
+
H
)
=
γ
N
s
−
(
1
−
ε
1
)
2
4
γ
D
,
γ
(
+
H
→
+
H
)
=
γ
N
s
−
(
1
+
ε
1
)
2
4
γ
D
,
(
11.81
)
where
γ
N
s
d
enotes the reaction rate densit
y
of the
N
s
N
p
rocess. Takin
g
accoun
t
of the decays and lepton-number-violating scattering processes, we finall
y
a
rrive at the correct Boltzmann equations
(
Giudic
e
et al
.
,
2004; Buc
h
m¨u
ll
er
et al.
,
2005a
,
2005b
;
Davidson et al.
,
2008
)
as follows:
sHz
d
Y
N
Y
Y
1
d
z
=
−
Y
N
Y
Y
1
Y
eq
N
Y
Y
1
−
1
γ
D
+2
γ
S
s
+
4
γ
S
t
,
s
H
z
d
Y
L
YY
d
z
=
Y
N
Y
Y
1
Y
eq
N
Y
Y
1
−
1
ε
1
γ
D
−
Y
L
YY
Y
eq
YY
2
γ
N
+2
γ
S
t
+
γ
S
s
Y
N
YY
1
Y
e
q
N
YY
1
,
(
11.82
)
w
h
e
r
e
γ
N
≡
γ
N
s
+
γ
N
t
, and a subtraction o
f
the on-shell contributions
f
ro
m
γ
N
s
has been done as in Eq.
(
11.81
)
. The final lepton number asymmetr
y
Y
L
YY
c
an then be obtained by solving the above Boltzmann equations.
11.3.4 Baryon Number
A
symmetry
So far another important lepton-number-violating reaction, the sphaleron
process, has not been considered. In the epoch o
f
lepto
g
enesis the sphalero
n
i
nteractions were in thermal equilibrium, so the
y
were ver
y
e
ffi
cient in con
-
verting the lepton number asymmetry into the baryon number asymmetry.
Since the sphaleron interactions conserve
(
B
−
L
)
, we shall derive the relation
betwee
n
B
and
(
B
−
L
).
T
he number density of the “
x
”
particles has been given in Eq.
(
11.58
),
f
rom which one ma
y
also write out the number densit
y
o
f
their antiparticle
s
by flippin
g
the si
g
nofthechemicalpotentia
l
μ
x
(
Kolb and Turner, 1990
)
.In
t
h
everyear
l
yUniverset
h
econ
d
ition
s
μ
x
/
T
1
an
d
m
x
/
T
1
are
b
ot
h
s
atis
fi
ed
f
or the
S
M particles, and hence the particle number as
y
mmetr
y
Δ
n
x
≡
n
x
−
n
x
c
an a
pp
rox
i
mate to
Δ
n
x
=
(
μ
x
/
T
)
g
x
T
3
/
6 for fermions or
Δ
n
x
=
(
μ
x
/T
)
g
x
T
3
/
3
for bosons. Let us consider the
S
Mwit
h
N
f
N
generation
s
of fe
rmi
o
n
sa
n
d
N
H
N
Hi
gg
s doublets. It consists o
f
the quark doublet
s
Q
i
,ri
gh
t-
h
anded up-t
y
pe quarks
U
i
UU
and down-t
y
pe quark
s
D
i
,
the le
p
ton doublets
i
a
n
d
rig
h
t-
h
an
d
e
d
c
h
arge
dl
epton
s
E
i
(
for
i
=1
,
2
,
·
·
·
,N
f
N
)
,andtheHigg
s
doub
l
ets
H
j
H
(
for
j
=1
,
2
,
···
,N
H
N
)
. At a sufficiently high temperature the
electroweak gauge symmetry is restored and the gauge interactions are in
thermal equilibrium. In this case the chemical potentials o
fg
au
g
e bosons ar
e
vanishin
g
,andthoseo
f
the components in the same quark, lepton or Hi
ggs
d
oublet should be equal. So the baryon and lepton numbers are given b
y
