Xing Zh., Zhou Sh. Neutrinos in Particle Physics, Astronomy and Cosmology
Подождите немного. Документ загружается.


386 11 Cosmological Matter-antimatter Asymmetr
y
transport
f
rom the outside into the inside o
f
the bubbles, and vice versa. How-
ever, both quarks and antiquarks can be reflected b
y
the bubble walls, and
the reflection and transmission coefficients of quarks and antiquarks are dif
-
f
erent due to
C
and
C
P violation. The bar
y
on number as
y
mmetries are the
n
generated in both the symmetric and symmetry-breaking phases, but the to
-
tal baryon number is still vanishing. Because of the rapid rate of sphaleron
processes in t
h
e symmetric p
h
ase, t
h
e correspon
d
in
gb
aryon num
b
er store
d
i
n
the left-handed quarks is finall
y
washed out. Therefore, the net bar
y
on num-
b
er asymmetry on
l
y resi
d
es in t
h
e symmetry-
b
rea
k
ing p
h
ase an
d
can surviv
e
u
ntil toda
y
i
f
the relevant sphaleron rate is
f
ar
f
rom thermal equilibrium. W
e
c
onclude that it is possible to dynamically generate the cosmological baryo
n
n
umber asymmetry in the
S
Mi
f
the phase transition is stron
g
ly o
f
the
fi
rst
order and the sphaleron processes are not very efficient.
(
Cohen
et al.
, 1993;
R
ubakov and Shaposhnikov, 1996
).
O
ne
fi
nds that the conditio
n
E
s
p
h
(
T
c
TT
)
/T
c
TT
>
45
o
r
v
(
T
c
TT
)
/T
c
TT
>
1, w
h
ic
h
l
eads to a li
g
ht Hi
gg
s boson wit
h
M
h
M
<
4
2
G
eV, should be satis
fi
ed in order to
a
ssure the sphaleron processes to be impotent. Current experimental boun
d
on t
h
eHi
gg
smassis
M
h
M
>
114 GeV
(
Nakamur
a
et al.
,
2010
)
. This contradic-
tion, to
g
ether with the fact that CP violation is badly suppressed due to the
s
trong hierarchy of quark masses, excludes the possibility of explaining the
observed bar
y
on number as
y
mmetr
y
o
f
the Universe within the
S
M. But a
n
umber of extensions of the SM with more sources of CP violation and mor
e
s
calar fields, such as the minimal supersymmetric standard model
(
MSSM
),
c
an realize baryogenesis at the electroweak scale
(
Riotto, 1998; Riotto an
d
Trodden, 1999
).
11.2.3
G
UT Baryogenesi
s
The uni
fi
cation o
f
electroma
g
netic and weak interactions in the
S
Mprove
s
to be very successful. Includin
g
quantum chromodynamics, the SM as a
SU
(
3
)
c
×
SU
(
2
)
L
×
U
(
1
)
Y
g
auge t
h
eory can we
ll d
escri
b
e
b
ot
h
strong an
d
e
l
ec-
troweak interactions. However, the direct product o
f
these symmetry
g
roups
m
eans that one has to introduce different
g
au
g
e couplin
g
constants for stron
g
,
weak and electromagnetic interactions. Howard Georgi and Sheldon Glashow
m
ade the
fi
rst step in embeddin
g
these three
f
undamental
f
orces into a
g
au
ge
theory with the compact symmetry group SU
(
5
)(
Georgi and Glashow, 1974
)
.
Subsequent developments along this line have taken advantage of other Lie
g
roups, suc
h
a
s
SO
(
10
)(
Fritzsch and Minkowski, 1975; Georgi, 1975
)
an
d
E
6
(
Slansky, 1981
)
. In such a grand unified theory
(
GUT
)
, the SM quarks an
d
l
eptons are usua
ll
y
g
roupe
d
into one mu
l
tip
l
et. Just
l
i
k
et
he
W
-boso
n
wh
i
ch
m
ediates char
g
ed-current weak interactions between a neutrino
fi
el
d
ν
L
a
n
d
the corresponding charged-lepton fiel
d
l
L
in the same
SU
(
2
)
L
d
oublet
,
anew
g
au
g
e
b
oson
X
i
nthe
G
UT may simultaneously interact with the quarks an
d
l
eptons in the same multiplet. Thus the deca
y
so
f
this
X
boso
nm
ust v
i
o
l
ate
both baryon and lepton numbers. In the original Georgi-Glashow model, fo
r

1
1.2 Typical Mechanisms o
f
Baryogenesis 387
example, the le
f
t-handed
f
ermions are embedded into the
5
a
n
d
10
r
epresen
-
tations of the S
U
(
5
)
group
:
5
=
⎛
⎜
⎛
⎛
⎜
⎜
⎜
⎜
⎜⎜
⎜
⎜⎜
⎝
⎜⎜
D
c
1
D
c
2
D
c
3
ν
e
e
⎞
⎟
⎞
⎞
⎟
⎟
⎟
⎟
⎟⎟
⎟
⎟⎟
⎠
⎟⎟
L
,
1
0
=
⎛
⎜
⎛
⎛
⎜
⎜
⎜
⎜
⎜⎜
⎜
⎜⎜
⎝
⎜⎜
0
U
c
2
UU
−
U
c
1
UU
u
1
d
1
−
U
c
2
UU
0
U
c
3
UU
u
2
d
2
U
c
1
UU
−
U
c
3
UU
0
u
3
d
3
−
u
1
−
u
2
−
u
3
0
E
c
−
d
1
−
d
2
−
d
3
−
E
c
0
⎞
⎟
⎞
⎞
⎟
⎟
⎟
⎟
⎟⎟
⎟
⎟⎟
⎠
⎟⎟
L
,
(
11.23
)
w
h
e
r
e
U
c
i
UU
L
,
D
c
i
L
a
n
d
E
c
L
w
i
th
i
b
ein
g
the color index denote the antiparticle
s
of the right-handed quark and charged-lepton singlets
,
Q
i
L
=(
u
i
,d
i
)
T
L
a
n
d
L
=
(
ν
e
,e
)
T
L
s
tand
f
or the le
f
t-handed quark and lepton doublets.
S
ince the
SU
(
5
)
gauge symmetry is not realized in nature, it must be spontaneousl
y
b
ro
k
en
d
own to
SU
(
3
)
c
×
SU
(
2
)
L
×
U
(
1
)
Y
which can be further broken dow
n
to
U
(
1
)
Q
as in the
S
M. The symmetry breakin
g
is achievable by introducin
g
a
scalar multiplet in the ad
j
oint representation, and its vacuum expectation
va
l
ue s
h
ou
ld b
eproper
l
yc
h
osen suc
h
t
h
at t
h
e
SU
(
3
)
c
×
SU
(
2
)
L
×
U
(
1
)
Y
s
ym-
m
etry is preserved.
A
fter spontaneous symmetry breakin
g
, the correspondin
g
gauge boso
n
X
a
c
q
u
i
res a mas
s
M
X
M
and mediates the interactions betwee
n
d
own-type quark singlets and lepton doublets
(
from the
5
r
epresentation
)
a
nd between charged-lepton singlets and quark doublets
(
from the 1
0
rep-
resentation
)
. This example illustrates that a GUT model may offer baryo
n
n
umber violation, which
f
ul
fi
lls the
fi
rst
S
akharov condition. In addition,
CP
violation simpl
yf
ollows the Koba
y
ashi-Maskawa mechanism as in the
SM
(
Kobayashi and Maskawa, 1973
)
.Therateso
f
X
→
D
+
an
d
X
→
Q
+
U
d
ecays are equal to those o
f
their
C
P-conju
g
ate processes at the tree level, bu
t
the
C
P-violatin
g
asymmetries can arise at the loop level. The third
S
akharov
c
ondition, or equivalently a departure from thermal equilibrium, will be sat-
i
s
fi
ed i
f
the decay rates o
fg
au
g
e bosons are smaller than the expansion rat
e
of the Universe
(
Kolb and Turner, 1990
)
.
T
he GUT baryogenesis seems to be promising in explaining the baryo
n
n
umber asymmetry, but this is not the case. The
(
B
+
L
)
-violating sphalero
n
processes, which must have been ver
y
efficient in the earl
y
Universe, ar
e
possible to erase all the preexisting baryon number asymmetry. One way ou
t
of this difficulty is to break the
(
B
−
L
)
conservation in the GUT, then a
n
a
symmetry in the
(
B
−
L
)
number should not be removed by the sphaleron
i
nteractions
(
Riotto and Trodden, 1999
)
. This is in some sense similar to th
e
l
epto
g
enesis mechanism, which will be discussed in detail in
S
ection 11.2.5.
11.2.4 Th
e
A
fflec
k-Din
e
M
ec
h
a
ni
s
m
We have seen that the minimal versions of electroweak and GUT baryoge
-
n
esis mechanisms are not very success
f
ul in explainin
g
the baryon numbe
r
a
s
y
mmetr
y
. In this case more and more interest has recentl
y
been focused
on baryogenesis via leptogenesis or via the Affleck-Dine mechanism. We shall

388 11 Cosmological Matter-antimatter Asymmetr
y
i
ntroduce the basic idea of the
A
ffleck-Dine mechanism in this subsection
,
a
nd then concentrate on lepto
g
enesis in the remainin
g
parts of this chapter.
C
onsider a theory of the complex scalar field, for which the Lagrangia
n
c
an be written as
(
Dine and Kusenko, 2004
)
L
φ
=(
∂
μ
φ
†
)(
∂
μ
φ
)
−
m
2
φ
†
φ
.
(
11.24
)
I
t
i
sobv
i
ous that
L
φ
is invariant under the phase rede
fi
nition
φ
→
φ
=
e
i
α
φ
w
i
th
α
bein
g
an arbitrary real constant. Thanks to the Noether theorem, we
h
ave the following conserved current:
J
μ
B
JJ
=i
(
φ
†
∂
μ
φ
−
φ
∂
μ
φ
†
)
,
(
11.25
)
w
h
ere t
h
eg
l
o
b
a
l
U
(
1
)
symmetry has been identified with the baryon number
.
It is worth mentionin
g
that the scalar
fi
elds with baryon and lepton numbers,
s
uch as the supersymmetric partners of quarks and leptons, are very commo
n
i
n a variety of supersymmetric theories
(
Affleck and Dine, 1985
)
. Note tha
t
L
φ
is also invariant under the
C
Ptrans
f
ormation
φ
↔
φ
†
, and hence th
e
theory is CP-invariant. Now we add the interaction terms described by
(
Din
e
a
nd Kusenko, 2004
)
L
i
nt
=
λ
(
φ
†
φ
)
2
+
φ
†
φ
3
+
δφ
4
+
h
.
c
.
,
(
11.26
)
w
h
e
r
e
a
n
d
δ
a
re in
g
eneral complex constants. Then both the baryon numbe
r
a
nd CP invariance can be violated by the
and
δ
terms in Eq.
(
11.26
)
.The
evo
l
ut
i
o
n
of t
h
e sca
l
a
r
fie
l
d
φ
(
x
)
in the homogeneous Universe is governed by
d
2
φ
(
t
)
d
t
2
+
3
H
d
φ
(
t
)
d
t
+
∂V
(
φ
)
∂φ
=
0
,
(
11.27
)
w
h
e
r
e
H
i
s the Hubble
p
arameter, an
d
V
(
φ
)
denotes the scalar potential. A
t
ear
l
ytimest
h
econ
d
ition
H
m held
,
so the scalar field was frozen at
φ
=
φ
0
w
i
th
φ
0
0bein
g
the expectation value. There
f
ore, the initial baryon num-
ber must have been vanishin
g
. When the Hubble parameter dropped far below
m, the scalar field started to oscillate, as indicated in Eq.
(
11.27
)
. Discardin
g
t
h
e quartic term in t
h
e potentia
l
,wecan
g
et
φ
(
t
)=
φ
0
(
mt
)
−
3
/
2
s
in
(
mt
)
fo
r
the radiation-dominated e
p
och with
H
=1
/
(2
t
)
o
r
φ
(
t
)
=
φ
0
(
mt
)
−
1
sin
(
m
t
)
fo
r
t
h
e
m
atte
r-
do
min
ated e
r
aw
i
th
H
=
2
/
(3
t
)
. Takin
g
φ
0
to be
r
eal a
n
d
a
ssum
i
n
g
a
n
d
δ
t
o be small coefficients, we solve Eq.
(
11.27
)
and obtain the
i
maginary part of
φ
as follows
(
Affleck and Dine, 1985
)
:
φ
I
=
a
r
Im
(
+
δ
)
φ
3
0
m
2
(
mt
)
3
/
4
s
in
(
mt
+
δ
r
)
(
11.28
)
wit
h
a
r
=
0
.
85
an
d
δ
r
=
−
0
.
9
1int
h
era
d
iation-
d
ominate
d
case
;
an
d
φ
I
=
a
m
Im
(
+
δ
)
φ
3
0
m
3
t
s
in
(
mt
+
δ
m
)
(
11.29
)

1
1.2 Typical Mechanisms o
f
Baryogenesis 389
w
i
th
a
m
=
0
.
85
an
d
δ
m
=1
.
54 in t
h
e matter-
d
ominate
d
case. Insertin
g
eit
h
er
E
q.
(
11.28
)
or Eq.
(
11.29
)
into the baryon-number current in Eq.
(
11.25
)
,w
e
a
rrive at a nonzero
b
aryon num
b
er at
l
arge times:
n
B
=
2
a
r
I
m
(
+
δ
)
φ
2
0
m
3
t
2
sin
(
δ
r
+
π
/
8)
,
(
radiation
)
,
n
B
=
2
a
m
I
m
(
+
δ
)
φ
2
0
m
3
t
2
s
in
(
δ
m
)
,
(
matter
)
.
(
11.30
)
The bar
y
on number stored in the scalar field will be converted to the bar
y
on
n
umber of the SM particles through various decays o
f
φ
. If the squark plays
the role o
f
the d
y
namical scalar
fi
eld,
f
or instance, it can deca
y
into the
S
M
q
uarks. The final amount of the bar
y
on number as
y
mmetr
y
depends on the
d
etails of the supersymmetric model and the inflation model
(
Affleck an
d
D
ine, 1985; Dine and Kusenko, 2004
).
11.2.5 Lepto
g
enes
is
The leptogenesis mechanism
(
Fukugita and Yanagida, 1986
)
is the most pop
-
u
lar mechanism o
f
baryo
g
enesis today, because it is closely related to th
e
s
eesaw mechanism o
f
neutrino mass
g
eneration. The
f
act that neutrinos ar
e
m
assive and le
p
tonflavorsaremixedim
p
lies that the minimal version of
the
S
M must be incomplete.
O
ne o
f
the most economical extensions o
f
th
e
SM is to introduce three ri
g
ht-handed neutrinos and allow lepton numbe
r
violation
(
see Section 4.3.1
)
. Such a canonical seesaw scenario can naturall
y
a
ccommodate baryo
g
enesis via lepto
g
enesis. Here we outline the basic idea o
f
l
epto
g
enesis.
A
more detailed description of the lepto
g
enesis mechanism will
b
e presente
d
in t
h
esu
b
sequent sections.
Th
eori
g
ina
ll
epto
g
enesis mec
h
anism wor
k
sint
h
e type-I seesaw mo
d
e
l
,
which has the following gauge-invariant neutrino mass terms:
−L
ν
=
L
Y
ν
YY
˜
HN
R
NN
+
1
2
N
c
R
NN
M
R
M
M
N
R
N
N
+h
.
c
..
(
11.31
)
A
fter spontaneous
g
au
g
e symmetry breakin
g
, one obtains the Dirac mass
m
atri
x
M
D
MM
=
Y
ν
YY
v
/
√
2
wit
h
v
≈
2
4
6G
e
V
. Provided the mass scale of
M
R
MM
i
ssi
g
ni
fi
cantly lar
g
er than that o
f
M
D
MM
,
t
h
e seesaw mec
h
anism wor
k
san
d
l
eads to the effective Majorana mass matrix of three light neutrino
s
M
ν
MM
≈
−
M
D
M
M
M
−
1
R
MM
M
T
D
M
M
.
G
iven
Y
ν
Y
Y
∼O
(
1
)
, the sub-eV mass scale o
f
M
ν
M
M
requires
M
R
M
M
∼
O
(
10
1
4
)
GeV. Let us denote the mass eigenstates and eigenvalues of three
h
eav
y
Ma
j
orana neutrinos to be
N
i
N
N
a
n
d
M
i
M
M
(
fo
r
i
=1
,
2
,
3)
, respectively.
Of course, the Majorana conditio
n
N
i
NN
=
N
c
i
NN
i
s fulfilled and lepton number is
violated. In the very early Universe the temperature was so hi
g
htha
t
N
i
NN
cou
l
d
be thermally produced and then stayed in equilibrium with the thermal bath.
A
s the temperature dropped below
M
i
M
M
,t
h
e
l
epton-num
b
er-vio
l
atin
gd
ecay
s
N
i
N
N
→
α
+
H
a
n
d
N
i
N
N
→
α
+
H
(
for
α
=
e
,
μ
,τ
)
would happen. The comple
x
Yukawa coupling matrix
Y
ν
Y
Y
may result in the CP-violating asymmetries

390 11 Cosmological Matter-antimatter Asymmetr
y
ε
i
≡
α
Γ
(
N
i
NN
→
α
+
H
)
−
Γ
(
N
i
NN
→
α
+
H
)
α
Γ
(
N
i
NN
→
α
+
H
)+
Γ
(
N
i
NN
→
α
+
H
)
(
11.32
)
via the interference between tree- and loop-level deca
y
amplitudes.
A
net lep
-
ton number asymmetry can then be generated from
ε
i
if the decays of
N
i
NN
a
r
e
out o
f
thermal equilibrium. The latter is satis
fi
able when the deca
y
rates o
f
N
i
N
N
a
re smaller than the expansion rate of the Universe. For the deca
y
of a heav
-
i
er
M
ajorana neutrin
o
N
2
NN
or
N
3
NN
,
the lepton-number-violating interactions of
t
h
e
l
i
gh
test
h
eavy Majorana neutrino
N
1
NN
may
b
e rapi
d
enou
gh
to was
h
out
the lepton number asymmetry originating from
ε
2
or
ε
3
. Hence onl
y
the CP-
vio
l
atin
g
asymmetry
ε
1
i
s survivable and relevant to lepto
g
enesis.
O
nce a net
l
epton number as
y
mmetr
y
is produced, the sphaleron interactions in therma
l
equilibrium will efficiently convert it into a baryon number asymmetry. Thi
s
c
onversion can be expressed as
(
Kolb and Turner, 1990
)
n
B
s
equilibriu
m
=
c
n
B
−
n
L
s
equi
l
i
b
riu
m
=
−
c
n
L
s
i
nitial
,
(
11.33
)
where
n
B
a
nd
n
L
s
tand respectivel
y
for the bar
y
on and lepton number den
-
s
ities,
s
denotes the entropy density of the Universe, and
c
=28
/
79
in t
h
e
S
M.
S
othe
fi
nal bar
y
on number as
y
mmetr
y
is determined b
y
the initial lep-
ton number asymmetry arising from the decays
(
and scattering processes
)
of
h
eavy Majorana neutrinos. Fig. 11.2 i
ll
ustrates t
h
ere
l
ation
b
etwee
n
B
a
n
d
L
i
nthe
p
resence o
f
ra
p
id s
p
haleron interactions. Note tha
t
n
L
s
h
ou
l
dbe
n
egative so as to yield
n
B
>
0
. The evolution o
f
n
L
an
d
n
B
can be figured
out
b
yso
l
vin
g
t
h
ere
l
evant Bo
l
tzmann equations.
11.3 Baryo
g
enesis via Lepto
g
enesi
s
This section is devoted to a detailed description o
f
baryo
g
enesis via lepto
-
genesis. First, we discuss the thermal or non-thermal production of heav
y
M
ajorana neutrinos
N
i
NN
.
Second, we calculate the CP-violating asymmetrie
s
ε
i
in the deca
y
so
f
N
i
NN
.Third,wewriteoutthe
f
ull Boltzmann equations to
d
escribe how the produced lepton and bar
y
on number as
y
mmetries evolve
.
F
inally, we make an analytical estimate of the net baryon number asymmetry
.
11.
3
.1 Thermal or Non-thermal Product
i
o
n
Because of the Yukawa interactions, heav
y
Ma
j
orana neutrinos
N
i
N
N
wit
h
masses
M
i
M
M
could abundantly be produced via the inverse decays
(
α
+
H
→
N
i
N
N
a
n
d
α
+
H
→
N
i
N
N
)
and scattering processes
(
α
+
U
→
Q
+
N
i
N
N
a
n
d
1
1.3
B
aryogenesis via
L
eptogenesis 39
1
B
(
a
)
(
b
)
B
−
L
>
0
B
−
L
=0
B
−
L
<
0
L
B
=
c
(
B
−
L
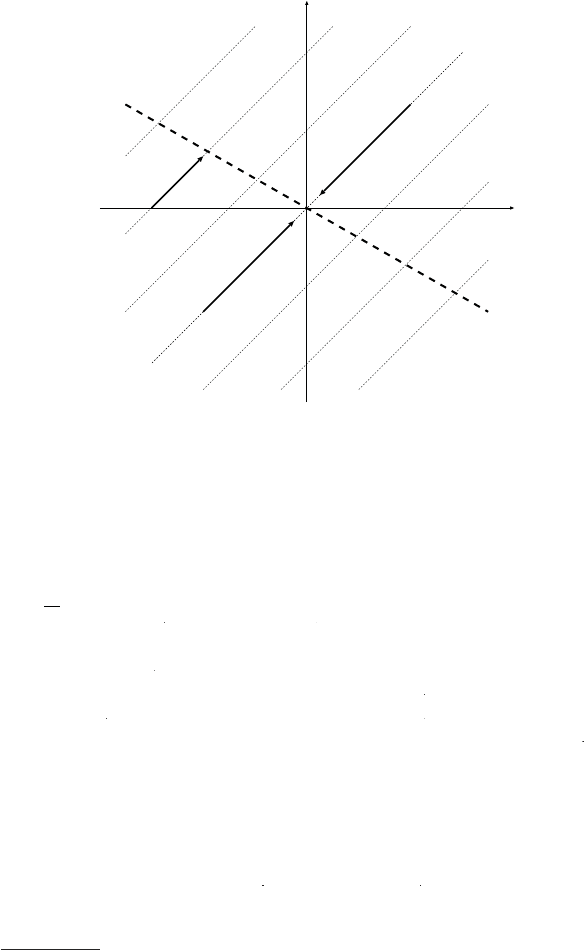
)
(equilibrium
)
Fig. 11.2 The relationship between baryon
(
B
)
and lepton
(
L
)
numbers. Th
e
sp
h
a
l
eron processes c
h
an
g
e
b
ot
h
B
a
n
d
L
a
l
on
g
t
h
et
h
in
d
otte
dl
ines wit
h
constan
t
(
B
−
L). The thick dashed line represents
B
=
c
(
B
−
L
), which should finall
y
be reached if the sphaleron interactions are in thermal equilibrium. Arrows
(
a
)
and
(
b
)
correspond to successful and unsuccessful leptogenesis mechanisms, respectively
(
Hamaguchi, 2002)
Q
+
U
→
α
+
N
i
NN
)
whe
n
T
M
i
M
M
was satis
fi
ed in the early Univers
e
3
.
It is usuall
y
assumed that the interaction rates o
f
these processes are rapi
d
enough to kee
p
N
i
N
N
i
n thermal e
q
uilibrium. Since the Yukawa interactions ar
e
responsible
f
or both the thermal production o
f
N
i
NN
and the out-o
f
-equilibrium
d
eca
y
so
f
N
i
NN
, whether the number densit
y
of
N
i
N
N
c
an reach the e
q
uilibrium
value is determined by the Yukawa coupling matrix of neutrino
s
Y
ν
YY
a
n
d
t
he
evolution behavior of Boltzmann equations
(
Luty, 1992; Pl¨umacher, 1997;
Buchm¨ulle
r
e
tal
.
,
2005a
)
.
I
n an inflation model the total energy of the early Universe was store
d
i
n the potential ener
g
yo
f
an in
fl
aton
fi
eld
φ
,w
h
ic
h
wou
ld d
eca
y
into t
h
e
SM particles at the minimum of the potential energy and then reheat the
U
niverse to t
h
e temperature
T
reh
TT
.
Th
eva
l
ue of
T
reh
T
T
sh
ou
ld b
e
l
arger t
h
an t
h
e
l
i
gh
test
h
eavy Majorana neutrino mass
M
1
∼
10
12
G
eV. This requirement is
f
ree from an
y
problems in those non-supers
y
mmetric seesaw models. In some
3
He
r
e
U
a
n
d
Q
de
n
ote the
SU
(
2
)
L
sin
g
let o
f
up-type quarks and the
SU
(
2
)
L
doublet of quarks, respectively. Their Yukawa interactions with the Higgs doublet
have been given in Eq.
(
2.46
)
. Note that there are also the production processes
invo
l
vin
g
t
h
ee
l
ectrowea
kg
au
g
e
b
osons. We s
h
a
ll d
iscuss suc
h
processes w
h
en we
derive the Boltzmann equations in Section 11.3.3
.

392 11 Cosmological Matter-antimatter Asymmetr
y
a
α
N
i
N
N
H
b
N
i
NN
H
b
a
α
a
α
N
i
NN
H
b
N
j
N
(a) (b) (c)
Fig. 11.3 The Feynman diagrams for the decays
N
i
NN
→
a
α
+
H
b
atthetreean
d
one-
l
oop
l
eve
l
s, w
h
ere
a
,
b
=
1
,
2
a
r
ethe
SU
(
2
)
indices of lepton and Higgs doublet
s
s
upersymmetric seesaw models, however, such a high reheating temperature
m
ay cause the overproduction of gravitinos — the supersymmetric partners
of gravitons
(
Weinberg, 1982; Ellis
et al
.
,
1982
)
.Apossiblewayoutisto
a
ssume that heavy Majorana neutrinos were non-thermally generated in th
e
s
upersymmetric case. I
f
N
i
N
N
a
n
d
φ
a
re coupled and the mass o
f
φ
sat
i
sfies
M
φ
M
>
2
M
i
MM
, then the deca
y
s
φ
→
N
i
NN
+
N
i
NN
a
re allowed
(
Lazarides and Shafi, 1991;
K
umekawa
e
tal.
,
1994
)
. After the Hubble parameter
H
b
ecame com
p
arable
to or smaller than the decay width o
f
φ
(
i.e.,
H
Γ
φ
Γ
=
λ
2
i
M
φ
M
/
4
π
w
i
th
λ
i
bein
g
the couplin
g
constant between
φ
a
n
d
N
i
NN
)
, the inflaton began to decay
(
Lazarides, 2002
)
. Then the reheating temperatur
e
T
reh
T
T
c
an
b
e
d
etermine
d
f
r
om
Γ
φ
Γ
=
H
t
ogether with Eqs.
(
9.30
)
and
(
9.31
):
T
reh
T
T
=
4
5
4
π
3
g
∗
1
/
4
Γ
φ
Γ
M
Pl
MM
,
(
11.34
)
where
g
∗
=
10
6
.
75 is the effective number of the relativistic degrees of freedo
m
i
n the SM, an
d
M
Pl
MM
≈
1
.
22
×
10
19
G
e
V
is the Planck mass. I
f
M
i
MM
T
reh
TT
h
o
ld
s
,
N
i
N
N
m
ust have deca
y
ed immediatel
y
a
f
ter its production. The number
d
ensit
y
o
f
N
i
NN
i
s roughly given by
n
N
i
≈
3
n
e
q
N
i
T
reh
T
T
/
(
2
M
i
MM
)
,wher
e
n
eq
N
i
d
enotes
the number densit
y
o
f
N
i
NN
in thermal equilibrium
(
Kumekaw
a
et al
., 1994
)
.
Although the non-thermal production mechanism of heavy Majorana neu-
trinos is interestin
g
, it depends on the details o
f
an in
fl
ation model. In the
f
ollowin
g
we shall only
f
ocus on the thermal lepto
g
enesis.
11.3.2 CP-violatin
gA
symmetries
The difference between the decay rate
s
Γ
(
N
i
NN
→
α
+
H
)
an
d
Γ
(
N
i
NN
→
α
+
H
)
vanis
h
es at t
h
etree
l
eve
l
,
b
ut it is nonzero at t
h
eone-
l
oop
l
eve
lb
ecause
d
irec
t
CP violation ma
y
arise from the interference between tree- and loop-leve
l
d
ecay amplitudes. The typical Feynman diagrams for
N
i
NN
→
a
α
+
H
b
d
ecays are
sh
own in Fi
g
. 11.3, w
h
ere t
h
e
SU
(
2
)
indice
s
a
a
n
d
b
r
e
f
er to the components
of lepton and Higgs doublets. One can see that the one-loop contribution
s
to the decay amplitudes include the sel
f
-ener
g
y and vertex corrections. For

1
1.3
B
aryogenesis via
L
eptogenesis 39
3
N
j
N
a
α
N
i
NN
H
b
N
j
N
H
b
a
α
N
i
NN
(
a
)(
b
)
Fi
g
. 11.4 The Feynman dia
g
rams
f
or the one-loop sel
f
-ener
g
ies o
f
heavy Majorana
neutrinos
N
i
NN
,
where the arc arrows denote the direction of the fermion flow
(
Denner
et al
.
,
1992. With permission from Elsevier; Dreiner
et al.
, 2010
)
the decays of
N
i
N
N
w
ith each lepton flavor in the final states, the correspondin
g
C
P-violatin
g
asymmetries are de
fi
ned as
ε
iα
≡
Γ
(
N
i
N
N
→
α
+
H
)
−
Γ
(
N
i
N
N
→
α
+
H
)
α
Γ
(
N
i
NN
→
α
+
H
)+
Γ
(
N
i
NN
→
α
+
H
)
,
(
11.35
)
whe
r
ethesu
mm
at
i
o
n
ove
r
the
SU
(
2
)
indices is implied. The total CP-
violatin
g
asymmetry in
N
i
NN
d
eca
y
s is therefore
ε
i
=
ε
ie
+
ε
iμ
+
ε
iτ
.
It i
s
easy to calculate the total decay rate o
f
N
i
NN
at t
h
etree
l
eve
l
:
Γ
i
Γ
Γ
≡
α
Γ
(
N
i
NN
→
α
+
H
)+
Γ
(
N
i
NN
→
α
+
H
)
=
Y
†
ν
YY
Y
ν
YY
i
i
8
π
M
i
MM
,
(
11.36
)
w
h
e
r
e
Γ
(
N
i
NN
→
α
+
H
)=
Γ
(
N
i
N
N
→
α
+
H
)
holds in the neglect of C
P
violation. Only the vertex corrections were considered in the early analysis
of leptogenesis
(
Fukugita and Yanagida, 1986; Luty, 1992
)
. The self-energy
c
orrections were found to be important
(
Flan
z
et al
.
,
1995
;
Covi
e
tal
.
,
1996
)
a
nd even dominant if the masses of heavy Majorana neutrinos are nearly
d
egenerate
(
Pilaftsis and Underwood, 2004
)
. Note that CP violation require
s
a
t least two different weak phases and two different stron
g
phases in th
e
d
ecay amplitudes. The weak phases come from the complex Yukawa coupling
mat
r
ix
Y
ν
YY
, while the stron
g
phases can be
g
enerated i
f
the lepton and Hi
ggs
d
oublets running in the loops are on their mass shells. This condition is alway
s
s
atisfied, becaus
e
N
i
N
N
a
re heavy enough as compared with the SM particles.
Let us be
g
in to calculate the one-loop sel
f
-ener
g
ies o
f
heavy Majorana
n
eutr
i
nos
N
i
NN
(
see Fig. 11.4 for the Feynman diagrams
)
. Because o
f
N
c
i
NN
=
N
i
NN
,
i
tisstrai
g
ht
f
orward to veri
f
y that the sel
f
-ener
g
ies can be expressed as
Σ
ij
(
/
p
/
/
)=
/
pP
/
/
L
PP
Σ
L
ij
(
p
2
)
+
/
pP
/
/
R
PP
Σ
R
ij
(
p
2
)
+
P
L
PP
Σ
M
∗
ij
(
p
2
)
+
P
R
PP
Σ
M
ij
(
p
2
)
,
(
11.37
)
w
h
e
r
e
Σ
R
ij
(
p
2
)
=
Σ
L
∗
ij
(
p
2
)
an
d
P
L
PP
,
R
≡
(
1
∓
γ
5
)
/
2. Th
eco
n
t
ri
but
i
o
n
f
r
o
m
t
h
e
F
eynman diagram in Fig. 11.4
(
a
)
is explicitly given by

394 11 Cosmological Matter-antimatter Asymmetr
y
−
i
Σ
(
a
)
ij
(
/
p
//
)
=
α
a,
b
−
i
(
Y
†
ν
YY
)
i
α
(
T
)
ba
−
i
(
Y
ν
YY
)
α
j
ab
×
d
4
k
(2
π
)
4
P
L
PP
i
(
/
p
//
+
/
k
//
)
(
k
+
p
)
2
+i
+
P
R
PP
i
/
k
//
+i
+
=
i
16
π
2
Y
†
ν
YY
Y
ν
YY
ij
B
0
(
p
2
,
0
,
0)
/
pP
//
R
PP
,
(
11.38
)
where
a
b
is the totall
y
antis
y
mmetric tensor with
12
=
−
21
=1,the
p
ositiv
e
i
nfinitesima
l
+
r
egularizes the propagators, and the masses of lepton and
H
i
gg
s
d
ou
bl
ets
h
ave
b
een omitte
d
.T
h
e two-point sca
l
ar Passarino-Ve
l
tma
n
f
unction is defined as
(
Passarino and Veltman, 1979
)
4
B
0
(
p
2
,
0
,
0
)=
Δ
E
−
ln
|
p
2
|
μ
2
+
2
+i
π
Θ
(
p
2
)
,
(
11.39
)
where
Θ
(
p
2
)
denotes the step function, an
d
Δ
E
≡
2
/
(4
−
D
)
−
γ
E
+ln
(4
π
)
w
i
th
D
b
eing t
h
e space-time
d
imension an
d
γ
E
b
eing t
h
eEu
l
er constant. T
h
e
F
eynman diagram in Fig. 11.4
(
b
)
can similarly be calculated:
−
i
Σ
(
b
)
i
j
(
/
p
//
)=
α
a,b
−
i(
Y
T
ν
YY
)
iα
(
T
)
ba
−
i(
Y
∗
ν
YY
)
α
j
ab
×
d
4
k
(
2
π
)
4
P
R
PP
i(
/
p
//
+
/
k
//
)
(
k
+
p
)
2
+i
+
P
L
PP
i
/
k
//
+i
+
=
i
16
π
2
Y
T
ν
YY
Y
∗
ν
YY
ij
B
0
(
p
2
,
0
,
0
)
/
pP
//
L
PP
.
(
11.40
)
A
lthough the divergence of the one-loop self-energie
s
Δ
E
is present, it may
d
irectly be removed as in the modified minimal subtraction scheme
(
M
S
)
.
A
fter the renormalization procedure, the finite self-ener
g
ies turn out to b
e
Σ
ij
(
/
p
//
)
=
/
p
//
K
ji
K
P
L
PP
+
K
ij
K
P
R
PP
A
(
p
2
)
,
(
11.41
)
whe
r
e
K
≡
Y
†
ν
Y
Y
Y
ν
Y
Y
is a
H
ermitian matrix
,
A
(
p
2
)
=
1
16
π
2
l
n
|
p
2
|
μ
2
−
2
−
i
π
Θ
(
p
2
)
.
(
11.42
)
N
ote that the step function in Eq.
(
11.42
)
should b
e
Θ
(
p
2
−
M
2
h
M
−
M
2
M
)
if
the lepton and Hi
gg
s masses are taken into account, implyin
g
that a
n
i
maginary part i
n
A
(
p
2
)
will appear if the particles in the loop are on their
m
ass shells. Note also that the ima
g
inary part o
f
A
(
p
2
)
is independent of the
r
e
n
o
rm
a
liz
at
i
o
n
sca
l
e
μ
.
4
T
he Passarino-Veltman functions are frequently encountered in the loop calcu-
lations
(
Denner, 1993
)
if the dimensional regularization is implemented
(
’t Hooft,
1
973
)
. In this scheme the dimension of the space-time is assumed to be
D
<
4
an
d
the limit
D
→
4
is taken for the final results.

1
1.3
B
aryogenesis via
L
eptogenesis 39
5
Now we are ready to compute the
C
P-violatin
g
asymmetries arisin
gf
ro
m
the interference between the tree-level amplitude and self-ener
g
y corrections.
In this case the overall decay amplitude o
f
N
i
NN
→
a
α
+
H
b
i
sasumofth
e
c
ontributions from Fig. 11.3
(
a
)
and Fig. 11.3
(
b
)
:
i
M
s
,
a
b
α
i
=
−
i
ab
j
=
i
u
(
q
)
P
R
PP
(
Y
ν
YY
)
αi
+(
Y
ν
YY
)
αj
S
(
/
p, M
//
j
M
)
Σ
ji
Σ
(
/
p
//
)
u
(
p
)
,
(
11.43
)
whe
r
ei
S
(
/
p, M
//
j
M
)
is the propagator of
N
j
N
. Note that onl
y
the truncated
G
reen
f
unctions contribute to the relevan
t
S
-matrix elements
,
so the summation i
n
E
q.
(
11.43
)
is over al
l
N
j
N
w
i
th
j
=
i
.
The overall decay amplitude for th
e
CP-conjugate proces
s
N
i
N
N
→
α
+
H
c
an be obtained in a similar wa
y
:
i
M
s
,a
b
α
i
=
−
i
a
b
j
=
i
v
(
q
)
P
L
PP
(
Y
∗
ν
Y
Y
)
αi
+
(
Y
∗
ν
Y
Y
)
αj
S
(
/
p, M
//
j
M
)
Σ
ji
Σ
(
/
p
//
)
u
(
p
)
.
(
11.44
)
I
nte
g
ratin
g
|M
s
,
ab
αi
|
2
a
n
d
|
M
s
,
ab
αi
|
2
over the phase space o
ffi
nal states, we
a
rrive at the
C
P-violatin
g
asymmetries induced by the sel
f
-ener
g
y corrections
:
ε
s
iα
=
1
2
M
i
MM
d
Π
q
Π
d
Π
k
(
2
π
)
4
δ
4
(
p
−
q
−
k
)
a,b
M
s
,
ab
α
i
2
−
M
s
,
a
b
α
i
2
α
Γ
(
N
i
NN
→
α
+
H
)+
Γ
(
N
i
NN
→
α
+
H
)
=
1
8
π
K
ii
K
j
=
i
M
i
M
M
M
2
i
MM
−
M
2
j
M
I
m
(
Y
∗
ν
YY
)
αi
(
Y
ν
YY
)
αj
K
ji
K
M
i
MM
+
K
ij
K
M
j
M
,
(
11.45
)
where d
Π
q
Π
≡
d
3
q
/
(2
π
)
3
(2
q
0
)
is the differential element of the phase space,
a
nd Eqs.
(
11.36
)
,
(
11.41
)
,
(
11.43
)
and
(
11.44
)
have been used. A sum of
ε
s
iα
over the lepton
fl
avors
g
ives rise to the total
C
P-violatin
g
asymmetry
ε
s
i
≡
α
ε
s
iα
=
1
8
π
K
ii
K
j
=
i
M
i
MM
M
j
M
M
2
i
MM
−
M
2
j
M
I
m
(
K
ij
K
)
2
.
(
11.46
)
N
ote t
h
at
ε
s
iα
an
d
ε
s
i
s
eem to be divergent provided the masses of two heav
y
Majorana neutrinos are degenerate
(
i.e.,
M
i
MM
=
M
j
M
)
. In this special case on
e
h
as to take account of the finite deca
y
widths o
f
N
j
N
in their propagators. The
d
ecay wi
d
t
h
s
Γ
j
Γ
actually serve as the regulator to make the CP-violatin
g
a
s
y
mmetries we
ll
-
b
e
h
ave
d
even in t
he
M
i
MM
=
M
j
M
limit. I
f
the mass splits
|
M
i
MM
−
M
j
M
|
a
re com
p
arable wit
h
Γ
i
ΓΓ
an
d
Γ
j
Γ
,
then the magnitudes of
ε
s
iα
a
nd
ε
s
i
c
an be resonantly enhanced. This observation is a starting point of th
e
resonant
l
eptogenesis mechanism
(
Pilaftsis and Underwood, 2004, 2005
).
W
e proceed to calculate the CP-violating asymmetries arising from th
e
i
nter
f
erence between the tree-level amplitude and one-loop vertex corrections
in
N
i
N
N
decays
(
see Fig. 11.5 for the Feynman diagrams
)
. The effective vertex
i
n Fig. 11.5
(
a
)
canbewrittenas
