Xing Zh., Zhou Sh. Neutrinos in Particle Physics, Astronomy and Cosmology
Подождите немного. Документ загружается.


376 11 Cosmological Matter-antimatter Asymmetr
y
c
ommon border.
S
uch violent annihilations would have produced numerou
s
ener
g
etic electrons and photons which must distort the CMB spectrum an
d
c
ontribute to the diffuse gamma rays with energies around 1 MeV. In this
s
ection we summarize t
h
e main astrop
h
ysica
l
an
d
cosmo
l
o
g
ica
l
o
b
servation
s
a
gainst the presence of a large amount of antimatter in our Universe, an
d
point out t
h
at t
h
ereisnowaytoso
l
ve t
h
is
b
aryon asymmetry pro
bl
em wit
h
in
the standard model
(
SM
)
of particle physics
.
11.1.1 Constraints
f
rom Antimatter Searche
s
It is well known that the
f
undamental interactions in nature are almost s
y
m
-
m
etric between
p
articles and anti
p
articles. In
p
articular, the CPT theore
m
s
tates that a particle and its antiparticle must have the same mass
(
and th
e
s
ame lifetime if they are unstable
)
. So it is rather reasonable to speculat
e
that the Universe should be symmetric about matter and antimatter, just as
D
irac
d
i
d
. However, it is unc
l
ear w
h
et
h
er t
h
e symmetry
b
etween partic
l
es an
d
a
ntiparticles at the microscopic level de
fi
nitel
y
leads to a matter-antimatte
r
s
ymmetric Universe at the macroscopic scale
(
Steigman, 1976
)
.Butonemay
a
sk such a meanin
gf
ul question: is our Universe symmetric between matte
r
a
nd antimatter based on the astrophysical and cosmolo
g
ical observations?
T
he searches for antimatter fall into two categories: one is the direct search
(
e.g., to search for antiprotons or antinuclei in the cosmic rays
)
and the other
i
s the indirect search
(
e.g., to detect the products from matter-antimatter
a
nnihilations
)
. The absence of antimatter on the Earth is obvious becaus
e
we
h
ave not seen an
y
proton-antiproton anni
h
i
l
ations in our ever
yd
a
yl
ives.
The largest amount of antimatter is stored in high-energy accelerators, wher
e
p
¯
p
p
p
or
e
+
e
−
c
o
ll
isions are use
d
to pro
d
uce new partic
l
es an
d
reactions. T
h
ose
s
uccess
f
ul activities o
f
human bein
g
s in outer space demonstrate that th
e
s
olar system is made of matter rather than antimatter.
A
nother compelling
evidence comes from the observation of cosmic rays. If there were a sizable
re
g
ion o
f
antimatter in our
g
alaxy or extra
g
alaxies, we would have discovered
a
ntiprotons or antinuclei in the cosmic ray experiments. The ratio of the an
-
tiproton
fl
ux to the proton
fl
ux is
f
ound to be o
f
O
(
1
0
−
4
)
in cosmic rays, an
d
this small value can be explained by identi
f
yin
g
antiprotons as the secondary
p
roducts from the reaction
p
+
p
→
p
+3
p
i
nitiated by the primary cosmic
ray protons. Furthermore, current experimental constraints on the
fl
uxes o
f
a
ntihelium and much heavier antielements are
(
Dolgov, 2001
)
:
Φ
[
He
]
Φ
[
He
]
<
2
×
1
0
−
6
,
Φ
[
A
(
Z>
2)]
Φ
[
A
(
Z>
2)]
<
2
×
10
−
5
,
(
11.1
)
where
A
(
Z>
2)
and
A
(
Z
> 2
)
stand respectively for the nuclei with mor
e
t
h
an two protons an
d
t
h
eantinuc
l
ei wit
h
more t
h
an two antiprotons. T
h
ese
c
onstraints a
g
ain indicate that stars or
g
alaxies in the
f
orm o
f
antimatter are
a
ctually absent in our Universe
.
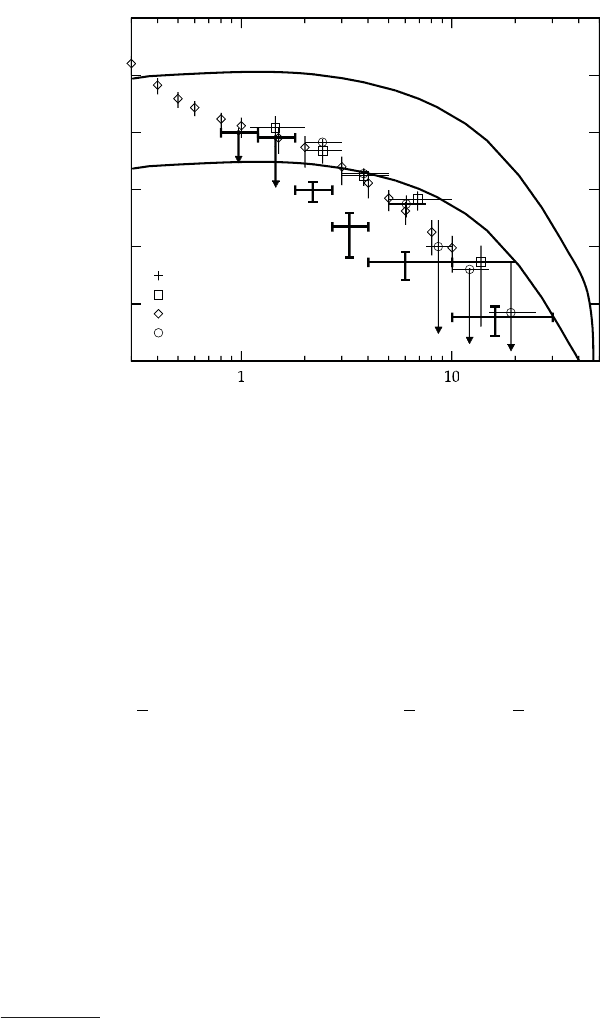
1
1.1 Baryon Asymmetry of the Universe 37
7
10
-6
10
-
5
10
-4
10
-
3
10
-2
10
-1
10
0
F
l
ux
[
p
h
otons cm
-2
s
-
1
M
e
V
-
1
sr
-
1
]
Ph
oton Ener
gy
[
MeV
]
CO
MPTEL
Schönfelder et al. (1980
)
Trom
bk
a et a
l
.
(
1977
)
W
h
ite et a
l
.
(
1977
)
d
0
=1
0
3
Mp
c
d
0
=20M
pc
Fig. 11.1 The observed spectrum of the diffusive gamma rays (Kappadath et a
l.
,
1
995
)
as compared with the calculated one from the matter-antimatter annihilation
(
Cohe
n
e
ta
l.
,
1998
)
, where
d
0
=20Mpc
(
upper solid curve
)
an
d
d
0
=10
3
Mpc
(
lower solid curve) denote the typical sizes of matter domains
T
he indirect searches also indicate the absence of antimatter in the whol
e
visible Universe. I
f
there are lar
g
ere
g
ions o
f
antimatter, violent matter
-
a
ntimatter annihilations are ex
p
ected to occur at the border
s
1
.
In th
e
m
atter-antimatter anni
h
i
l
ation neutra
l
an
d
c
h
arge
d
pions can
b
ecopious
l
y
g
enerated. The decays o
f
neutral pions via π
0
→
2
γ
g
ive rise to a di
ff
us
e
gamma-ray background. On the other hand, the decays of charged pions vi
a
π
±
→
μ
±
+
ν
μ
(
ν
μ
)
together with
μ
±
→
e
±
+
ν
μ
(
ν
μ
)
+
ν
e
(
ν
e
)
produce a lo
t
of electrons, positrons and neutrinos.
A
ll these annihilation products have
very similar energy spectra, and their number densities are peaked around
100
∼
2
00 MeV. The most use
f
ul component
f
or probin
g
matter-antimatter
a
nnihilation is the diffuse gamma rays
(
Steigman, 1976
)
. But a measuremen
t
of the diffuse gamma rays can only impose an upper limit on the matter
-
a
ntimatter annihilation, because the
C
ompton scatterin
g
o
f
the starli
g
ht and
c
osmic ray electrons may also contribute to the
g
amma rays.
A
careful analy
-
s
is reveals that the size of matter domain should be as large as
d
0
=10
3
M
pc
,
which is just the typical scale of the visible Universe
(
Cohe
n
et al
., 1998
)
.
The strate
g
y of this analysis is to assume that the total baryon number o
f
theUniverseiszero
,
and the Universe is divided into domains of matter or
1
T
he annihilation might not happen if matter and antimatter were well sepa-
rate
d
.Int
h
is case,
h
owever, one
h
as to resort to ver
y
contrive
d
mec
h
anisms so as
to make matter and antimatter far away from each other.

378 11 Cosmological Matter-antimatter Asymmetr
y
a
ntimatter wit
h
t
h
et
y
pica
ld
imension
d
0
. Then the spectra o
f
the di
ff
us
e
g
amma rays comin
g
from the matter-antimatter annihilation in the epoch o
f
recombination can be calculated, redshifted and compared with current ob-
s
ervational data. The results are shown in Fi
g
. 11.1,
f
rom which one can se
e
that the case wit
h
d
0
=
1
0
3
Mpc is more consistent with data, implying tha
t
the visible Universe contains only matter and no sizable regions of antimatter
(
Cohen
et al.
,
1998
).
11.1.2 Observations
f
rom the CMB and BBN
In the standard model o
f
cosmolo
g
y the anisotropies o
f
the
C
MB and th
e
primordial abundances of li
g
ht elements from the Bi
g
Ban
g
nucleosynthesi
s
(
BBN
)
can be computed with the baryon number density
η
a
sanimportant
i
nput parameter
(
Kolb and Turner, 1990; Dodelson, 2005; Weinberg, 1972,
2
008
)
. It is therefore possible to strictly determine or constrain the value o
f
η
f
rom the precision measurements of the CMB and light element abundances
.
T
he
C
MB
f
ormed shortl
y
a
f
ter the time o
f
recombination, when protons
a
nd electrons combined to form neutral hydrogen atoms. From this momen
t
on t
h
ecosmo
l
ogica
l
t
h
erma
lb
at
hb
ecame transparent to re
l
ic p
h
otons, s
o
they le
f
tthesur
f
ace o
f
last scatterin
g
and
f
reely propa
g
ated until today.
H
ence the anisotropies of the CMB are mainl
y
determined b
y
the d
y
namics
of t
h
et
h
e
rm
a
l
bat
h
befo
r
e
r
eco
m
b
in
at
i
o
n. Th
eva
l
ue of
η
is actua
ll
yextracte
d
f
rom the an
g
ular power spectrum o
f
the
C
MB, in particular its acousti
c
p
eaks. An intuitive
p
icture for the formation of acoustic
p
eaks is as follows
:
(
1
)
the density fluctuations in the early Universe induced the gravitational
i
nstabilities, and the baryon
fl
uid
f
allin
g
into the
g
ravitational potential wells
were compressed and then heated up;
(
2
)
this hot baryon fluid expanded and
radiated photons, and thus it gradually cooled down;
(
3
)
the gravity overtoo
k
the decreasin
g
radiation pressure a
g
ain and initiated another compressin
g
p
h
ase. It was just t
h
e competition
b
etween t
h
e gravity an
d
ra
d
iation pressur
e
that induced the acoustic oscillations in the bar
y
on
fl
uid, which would be
f
rozen in the CMB after the decouplin
g
of photons from the baryon matter.
The acoustic peaks in the angular power spectrum of the CMB serve as
a
c
onsequence of the sound waves in the primordial baryon fluid
(
Grupe
n
et
a
l
.
,
2005
)
. Given the five-year WMAP results, the ratio of cosmic baryon and
photon number densities has been determined to a good degree of accurac
y
(
Komats
u
et al
.
,
2009
)
2
η
≡
n
B
−
n
B
n
γ
=
(
6
.
21
±
0
.
1
6
)
×
10
−
10
,
(
11.2
)
whe
r
e
n
B
=0holdstoda
y
,asalread
y
discussed in
S
ection 11.1.1.
2
T
he WMAP Collaboration has recently released the seven-year data
(
Komatsu
e
ta
l.
,
2010
)
, in which the central value of the baryon energy density is the same a
s
that given in the five-year data.
1
1.2 Typical Mechanisms o
f
Baryogenesis 379
T
he result obtained in Eq.
(
11.2
)
is in good agreement with the results
extracted from the measurements of the primordial abundances of li
g
ht ele
-
m
ents based on the BBN theory. As shown in Fig. 9.1 and in Eqs.
(
9.48
)
and
(
9.49
)
, the cosmic baryon-to-photon rati
o
η
ca
n
be dete
rmin
ed f
r
o
m
bot
h
t
h
e
m
easured
4
H
emassfractionandtheobservedDand
7
L
i number fractions.
The BBN concordance range o
f
η
i
s consistent very well with the CMB mea
-
su
r
e
m
e
n
tof
η
a
tthe95
%
confidence level
(
Nakamura
et al
., 2010
)
, pointing
to
η
≈
6
×
1
0
−
1
0
.
Because the time for the BBN to happen
(
t
1
s
)
is s
o
d
ifferent from that for the CMB to form
(
t
∼
3
.
8
×
10
5
yr
)
, an agreement be
-
twee
n
t
h
eva
l
ues of
η
o
btained
f
rom these two epochs is particularly strikin
g.
The dynamical origin of this baryon number asymmetry of the Universe
(
i.e.,
b
aryogenesi
s
)
is an important but unsolved problem in particle physics an
d
c
osmolo
g
y. We shall brie
fl
y describe a
f
ew typical mechanisms o
f
baryo
g
enesis
i
n the next section
.
11.2 Typical Mechanisms of Baryogenesis
E
ven if the baryon number asymmetry were naively taken as one of the initia
l
c
onditions o
f
the Universe, it would unavoidably be erased in the in
fl
ation era.
H
ence a dynamical mechanism
f
or baryo
g
enesis is necessary, and it is amon
g
the most fundamental problems in modern particle physics and cosmology
.
In this section we
fi
rst introduce
S
akharov’s three necessary conditions
f
o
r
baryo
g
enesis, and then
g
ive an overview of a few intri
g
uin
g
mechanisms pro
-
posed so far to realize those conditions and explain the observed baryo
n
n
umber as
y
mmetr
y
o
f
the Universe
.
11.2.1
S
akharov
C
onditions
In 1967,
A
ndrei Sakharov proposed three necessary conditions for baryo
g
en-
esis
(
Sakharov, 1967
)
. They are summarized as follows.
(
1
)
B
ar
y
on num
b
er vio
l
ation
.
I
f
all the
f
undamental interactions preserve
d
the bar
y
on number
B
,
it would be obvious that the Universe with an initia
l
co
n
d
i
t
i
on
B
=
0 could not gain any baryon number excess. In the SM both
t
h
e
l
epton num
b
e
r
L
a
n
d
t
h
e
b
ar
y
on num
b
e
r
B
a
r
eco
n
se
r
ved at the clas-
s
ical level. But these two accidental s
y
mmetries are not as fundamental a
s
the conservation of electric charges which is guaranteed by the local gaug
e
s
ymmetry. In fact, it has been found that only the combination
(
B
−
L
)
i
s exactly conserved in the SM after taking into account the axial anomaly
a
nd the nontrivial vacuum structure of non-Abelian gauge theories
(
’t Hooft,
1
976
)
. Hence the baryon-number-violating interactions already exist in the
m
inimal version of the SM, but at the non-
p
erturbative level
.
(
2
)
C
and
C
Pviolation.Byde
fi
nition, the baryon number o
f
a
g
ive
n
particle
(
B
)
is opposite to the baryon number of its antiparticle
(
−
B
)
.If
the charge-conjugate symmetry
(
C
)
is conserved, the interaction rate for a
380 11 Cosmological Matter-antimatter Asymmetr
y
reaction
g
eneratin
g
an amount o
f
B
m
ust be equal to that
f
or its char
g
e
-
c
onju
g
ate process which produces the same amount of
−
B
.
In this case th
e
n
et baryon number of the system remains vanishing. One usually encounter
s
the chiral interactions which are relevant to both
C
and P properties o
f
the fermion fields. For example, the left- and right-handed fermions have
d
ifferent interactions in the SM. Let us explain why th
e
B
- and C-violating
i
nteractions are not su
ffi
cient
f
or the baryon number
g
eneration.
C
onsider
the B-violating decays
X
→
χ
L
+
ψ
L
a
n
d
X
→
χ
R
+
ψ
R
t
ogether with thei
r
CP-conjugate processes
X
→
χ
R
+
ψ
R
a
n
d
X
→
χ
L
+
ψ
L
,w
h
ere t
h
e
b
aryo
n
n
umbers o
f
the involved particles are assi
g
ned to be
B
(
X
)=
B
(
X
)
=0,
B
(
χ
L
,
R
)=
B
(
ψ
L
,
R
)
=+1an
d
B
(
χ
L
,
R
)
= B
(
ψ
L
,
R
)
=
−
1. We further assume
C
violation; i.e.
,
Γ
(
X
→
χ
L
+
ψ
L
)
=
Γ
(
X
→
χ
L
+
ψ
L
)
and
Γ
(
X
→
χ
R
+
ψ
R
)
=
Γ
(
X
→
χ
R
+
ψ
R
)
hold for these four decay rates. If CP is a good symmetry
,
h
owever
,
we must have
Γ
(
X
→
χ
L
+
ψ
L
)
=
Γ
(
X
→
χ
R
+
ψ
R
)
,
Γ
(
X
→
χ
R
+
ψ
R
)
=
Γ
(
X
→
χ
L
+
ψ
L
)
,
(
11.3
)
i
mplying that a net baryon number excess cannot be generated. Therefore, a
s
uccess
f
ul baryo
g
enesis mechanism requires both
C
and
C
P violation.
S
inc
e
the weak interactions violate both C and CP s
y
mmetries, the SM itself fulfills
the second
S
akharov condition too.
(
3
)
Departure
f
rom thermal equilibriu
m
.
G
iven a bar
y
on number as
y
mme-
tr
y
in the earl
y
Universe, its evolution with the temperature must be take
n
i
nto account. If the whole system stays in thermal equilibrium, the ensembl
e
a
vera
g
eo
f
the baryon number can be expressed as
B
=
N
−
1
Tr
B
e
−
βH
=
N
−
1
Tr
(
CPT
)
B
(
CPT
)
−
1
(
CPT
)
e
−
β
H
(
CPT
)
−
1
=
N
−
1
Tr
(
−
B
)e
−
βH
=
−
B
(
11.4
)
wit
h
N
≡
Tr
e
−
βH
,
where we have assumed the Hamiltonian
H
to be
i
nvariant under CPT
(
i.e.,
(
CPT
)
H
(
CPT
)
−
1
=
H
)
and used the fact that
t
h
e
b
ar
y
on num
b
e
r
B
is odd under C and CPT
(
i.e.,
(
CPT
)
B
(
CPT
)
−
1
=
−
B
)
(
Bernreuther, 2002
)
. Then we arrive a
t
B
=
0fromEq.
(
11.4
)
. In practice,
a
process will depart from thermal equilibrium if its interaction rate is smaller
than the expansion rate o
f
the Universe.
C
PT is a good symmetry in a local quantum field theory which is Lorentz
-
i
nvariant and possesses a Hermitian Lagrangian. Most viable mechanisms of
baryo
g
enesis respect the above
S
akharov conditions. But an exception ca
n
a
lways be found, for instance, by discarding the CPT theorem
(
Dolgov, 1992
)
.
11.2.2 Electroweak Baryogenesi
s
A
n immediate attempt to account for the cosmolo
g
ical baryon asymmetr
y
s
hould be made in the SM, where there exists baryon number violation to-
1
1.2 Typical Mechanisms o
f
Baryogenesis 38
1
g
ether with
C
and
C
P violation. In addition, a departure
f
rom thermal equi-
l
ibrium can be achieved to assure the
g
enerated baryon asymmetry to surviv
e
i
f the electroweak phase transition is of the first order. Such a baryogenesi
s
m
echanism is called the electroweak baryogenesis
(
Kuzmi
n
et al
., 1985
)
.
First, let us show how the bar
y
on number is violated in the standard elec
-
trowea
k
t
h
eory. T
h
e
k
ey point
h
ereisc
l
ose
l
yre
l
ate
d
to an important aspec
t
o
f
quantum
fi
eld theories — the symmetry breakin
g
induced by the quantum
a
nomal
y
. For instance, the deca
y
rate o
f
π
0
→
2
γ
c
an be inter
p
reted as
a
n
atural consequence of the chiral symmetry breaking caused by the anomaly
.
In a consistent quantum
fi
eld theor
y
one must make sure that the quantum
a
nomaly arising from the triangle diagrams is absent, so as to guarantee th
e
renormalizability of the theory itself
(
Adler, 1969; Bell and Jackiw, 1969
)
.For
i
llustration, we consider quantum electrod
y
namics with a massless
f
ermion
Ψ
,
for which the Lagrangian can be derived from Eq.
(
2.4
)
by setting
m
=
0.
In this case one may veri
f
y that the La
g
ran
g
ian is invariant under the trans-
fo
rm
at
i
o
n
s
Ψ
→
Ψ
=
e
−
i
α
Ψ
a
n
d
Ψ
→
Ψ
=e
−
i
αγ
5
Ψ
,
where
α
i
s an arbitrar
y
rea
l
constant. T
h
en t
h
eNoet
h
er t
h
eorem
l
ea
d
sustot
h
e conserve
d
axia
l
cu
rr
e
n
t
J
μ
5
J
(
x
)
≡
Ψ
(
x
)
γ
μ
γ
5
Ψ
(
x
)
in addition to the conserved vector current
J
μ
(
x
)
≡
Ψ
(
x
)
γ
μ
Ψ
(
x
)
. Now we examine how the quantization of the theor
y
violates the conservation of the axial current
(
i.e.
,
∂
μ
J
μ
5
JJ
(
x
)
= 0). By means of
the path-inte
g
ral quantization, we should consider the
f
unctional inte
g
ration
over the
g
au
g
e and fermion fields:
Z
=
[
d
A
μ
][
d
Ψ
][d
Ψ
]
ex
p
*
i
d
4
x
−
1
4
F
μν
F
μν
F
+
Ψ
i
/
DΨ
//
)
(
11.5
)
wit
h
/
D
//
≡
γ
μ
(
∂
μ
−
i
eA
μ
)
being the covariant derivative. Note tha
t
Z
is inde-
pendent of all the fields after integration, hence it should be invariant unde
r
t
h
et
r
a
n
sfo
rm
at
i
o
n
Ψ
→
Ψ
=
e
−
i
α
(
x
)
γ
5
Ψ
,w
h
er
e
α
(
x
)
is an arbitrary rea
l
f
unction of x.
A
fter applyin
g
such a local chiral transformation to the ri
g
ht-
h
andsideofEq.
(
11.5
)
, we find two additional contributions to the total
L
a
g
ran
g
ian. The
fi
rst one arises
f
rom the covariant-derivative ter
m
Δ
L
1
=
Ψ
i
/
DΨ
//
−
Ψ
i
/
DΨ
//
=
−
α
(
x
)
∂
μ
J
μ
5
JJ
(
x
)
,
(
11.6
)
w
h
ere t
h
e tota
l
-
d
erivative term
h
as
b
een omitte
d
.T
h
eot
h
er contri
b
utio
n
c
omes from the measure of fermionic integration
(
Fujikawa, 1979
)
[
d
Ψ
]
d
Ψ
=
Det
e
2i
α
(
x
)
γ
5
[
d
Ψ
][d
Ψ
]
,
(
11.7
)
where the determinant o
f
thematrixistakenoverthes
p
in and s
p
ace-tim
e
i
ndices; i.e.,
[
exp
{
2i
α
(
x
)
γ
5
}
]
mx,n
y
≈
1+2i
α
(
x
)[
γ
5
]
mn
δ
4
(
x
−
y
)
holds for th
e
i
n
fi
ni
tes
im
al
α
(
x
)
.UsingDet
M
=exp
[
Tr
(
M
)]
, one can exponentialize th
e
d
eterminant in Eq.
(
11.7
)
, which contributes to the total Lagrangian a
s
Δ
L
2
=
2
α
(
x
)
Tr
[
γ
5
]
δ
4
(
x
−
x
)
.
(
11.8
)
382 11 Cosmological Matter-antimatter Asymmetr
y
H
ere the delta
f
unction yields in
fi
nity, while the trace is vanishin
g
.Inorderto
m
ake Eq.
(
11.8
)
meaningful, we may introduce the gauge-invariant differentia
l
opera
t
or ex
p
{−
(i
/
D
//
)
4
/
M
4
}
to regularize the trace and delta function and then
set
M
→
+
∞
(
Fujikawa, 1979
)
. The result is
Δ
L
2
=
α
(
x
)
e
2
8
π
2
F
μν
F
˜
F
μν
,
(
11.9
)
whe
r
e
˜
F
μν
F
≡
ε
μνρ
σ
F
ρ
σ
/
2 is the dual o
f
the
fi
eld stren
g
th wit
h
ε
μνρ
σ
b
ein
g
a
totally antisymmetric tensor. By requirin
g
the
g
eneratin
gf
unctional in
E
q.
(
11.5
)
to be invariant under the local chiral transformation, we have
Δ
L
1
+
Δ
L
2
=0
f
or the arbitrary real
f
unctio
n
α
(
x
)
, implying the anomaly
of the axial current
(
Fujikawa, 1979, 1980
)
∂
μ
J
μ
5
J
(
x
)
=
e
2
8
π
2
F
μν
F
˜
F
μν
.
(
11.10
)
H
ence the symmetry at the classical level, which leads to
∂
μ
J
μ
5
J
(
x
)
=0,is
vio
l
ate
d
at t
h
e quantum
l
eve
l
.Duetot
h
e axia
l
anoma
l
y, t
h
e
l
epton an
d
baryon numbers are not exactly conserved
(
’t Hooft, 1976
)
. Consider th
e
f
ermions in the SM, for which the Lagrangian has been given in Eq.
(
2.32
)
.
The bar
y
on- and lepton-number currents can be de
fi
ned as
J
μ
B
JJ
≡
i
Q
i
L
γ
μ
Q
i
L
+
U
i
R
U
U
γ
μ
U
i
R
UU
+
D
i
R
γ
μ
D
i
R
,
J
μ
L
JJ
≡
α
α
L
γ
μ
α
L
+
E
α
R
γ
μ
E
α
R
,
(
11.11
)
w
h
ere
i
(
=
1
,
2
,
3)
an
d
α
(
=
e
,μ,τ
)
stand for the quark and lepton flavors,
respectivel
y
. Note that the bar
y
on number o
f
each quark with a de
fi
nite color
i
s assigned to be
1
/
3, which has been cancelled out b
y
the summation over
the color index of quark fields. Taking the divergences of baryon- and lepton-
n
um
b
er currents, we o
b
tain
∂
μ
J
μ
B
JJ
=
1
2
i
∂
μ
−
Q
i
γ
μ
γ
5
Q
i
+
U
i
γ
μ
γ
5
U
i
+
D
i
γ
μ
γ
5
D
i
,
∂
μ
J
μ
L
JJ
=
1
2
α
∂
μ
−
α
γ
μ
γ
5
α
+
E
α
γ
μ
γ
5
E
α
,
(
11.12
)
whe
r
ewehaveused
P
L
PP
,
R
=(
1
∓
γ
5
)
/
2a
n
dt
h
eco
n
se
r
vat
i
o
n
of vecto
r
cu
rr
e
n
ts.
A
long the same line in deriving Eq.
(
11.10
)
and making use of the covariant
d
erivatives in Eq.
(
2.33
)
,onemayverify
∂
μ
J
μ
B
J
J
=
∂
μ
J
μ
L
J
J
=
N
f
N
3
2
π
2
−
g
2
W
i
μν
W
˜
W
iμ
ν
+
g
2
B
μ
ν
˜
B
μ
ν
(
11.13
)
w
i
th
W
i
μν
W
a
n
d
B
μ
ν
b
ein
g
the stren
g
ths o
f
SU
(
2
)
L
a
n
d
U
(
1
)
Y
g
au
g
e
fi
elds
,
respectively. Note that the number of fermion generations i
s
N
f
N
=3
in th
e

1
1.2 Typical Mechanisms o
f
Baryogenesis 383
S
M. Now it becomes evident that both the bar
y
on number
B
≡
7
d
3
x
J
0
B
JJ
(
x
)
a
nd the le
p
ton number
L
≡
7
d
3
x
J
0
L
J
J
(
x
)
are violated, but the combinations
(
B
−
L
)
an
d
Δ
α
≡
B
/
3
−
L
α
are conserve
d,
w
h
ere
L
α
(
fo
r
α
=
e
,μ,τ
)
denotes
the lepton flavor number. Furthermore, the
(
B
+
L
)
-violating interactions are
u
niquely determined by the gauge fields on the right-hand side of Eq.
(
11.13
)
.
A
s we shall show later on, such kinds of interactions are highly suppresse
d
a
tt
h
e zero temperature
b
ut can
b
een
h
ance
d
at a temperature
h
i
gh
er t
h
a
n
the electroweak scale
.
S
econd, let us estimate the rates of
B
-violating interactions in the S
M
a
t both zero and
fi
nite temperatures. Note that the terms on the ri
g
ht-hand
s
ide of Eq.
(
11.13
)
can be written as a total divergence
∂
μ
J
μ
B
JJ
=
∂
μ
J
μ
L
JJ
=
N
f
N
32
π
2
−
g
2
∂
μ
K
μ
+
g
2
∂
μ
K
μ
,
(
11.14
)
whe
r
e
K
μ
=2
ε
μνρσ
(
∂
ν
W
i
ρ
W
)
W
i
σ
WW
+
1
3
gε
ijk
W
i
ν
WW
W
j
ρ
W
W
k
σ
WW
,
K
μ
=2
ε
μνρσ
(
∂
ν
B
ρ
)
B
σ
.
(
11.15
)
Integrating Eq.
(
11.15
)
over the three-space and using the definition of baryon
a
nd lepton numbers, one may then relate the chan
g
es o
f
baryon and lepton
n
umbers in a unit time to those o
f
the
C
hern-
S
imons numbers
:
Δ
B
=
Δ
L
=
N
f
N
(
Δ
N
CS
N
N
−
Δ
n
CS
)
,
(
11.16
)
where the
C
hern-
S
imons numbers are de
fi
ned as
N
CS
NN
=
−
g
2
16
π
2
d
3
x
2
ε
lm
n
Tr
(
∂
l
W
m
W
W
)
W
n
W
W
−
2
3
i
gW
l
WW
W
m
W
W
W
n
W
W
,
n
CS
=
−
g
2
1
6
π
2
d
3
x
ε
l
mn
(
∂
l
B
m
)
B
n
.
(
11.17
)
In Eq.
(
11.17
)
we have defined
W
l
WW
≡
τ
i
W
i
l
WW
a
n
d used
l
,
m
a
n
d
n
to de
n
ote the
s
patial components. Now it is straightforward to verify that
n
CS
i
s gauge
-
i
nvariant,
b
ut
N
CS
NN
is not.
U
n
d
er t
he
SU
(
2
)
L
g
auge transformation
W
m
WW
=
U
(
θ
)
W
m
WW
U
−
1
(
θ
)
−
i
g
[
∂
m
∂
U
(
θ
)]
U
−
1
(
θ
)
,
(
11.18
)
w
h
e
r
e
U
(
θ
)
≡
e
x
p
{
−
i
θ
i
(
x
)
τ
i
}
i
saun
i
tar
y
matr
i
x,
N
CS
NN
t
r
a
n
sfo
rm
sas
δN
CS
N
N
=
1
24
π
2
d
3
x
ε
lmn
Tr
(
∂
l
U
)
U
−
1
(
∂
m
∂∂
U
)
U
−
1
(
∂
n
∂
U
)
U
−
1
.
(
11.19
)
A
lthou
gh
N
CS
NN
d
epends on the
g
au
g
e, it is actually invariant under the in
-
finitesimal transformations
(
Weinberg, 1996
)
. As pointed out by Gerardu
s

384 11 Cosmological Matter-antimatter Asymmetr
y
’t Hooft, the vacuum structure of the non-
A
belian
g
au
g
etheoriesisrather
c
omplicated in the sense that there exists an infinite number of topolo
g
icall
y
d
istinct vacua whose field configurations are just characterized by the Chern
-
Simons numbers
(
’t Hooft, 1976; Callan
et al
.
,
1976; Jackiw and Rebbi, 1976
)
.
In this case the Chern-Simons numbers, and thus the bar
y
on and lepton num-
bers, will be changed if a transition between two different vacua takes place
.
To
b
eexp
l
icit, we consi
d
er a pur
e
S
U
(
2
)
Yang-Mills theory, in which the fiel
d
s
trength of the vacuum state should satisfy the condition
W
μν
W
≡
τ
i
W
i
μν
W
=0
a
tanytime.Int
h
e temporary
g
au
g
e
W
0
WW
=
τ
i
W
i
0
WW
=0,onecan
fi
nd that the
gauge transformations in Eq.
(
11.18
)
now have to fulfil
l
∂
0
U
(
x
)
=0
(
i.e., U
(
x
)
i
s time-independent
)
. Hence the gauge field
s
W
i
WW
(
x
)
=
−
i
g
−
1
[
∂
i
∂
U
(
x
)]
U
−
1
(
x
)
obviousl
y
satis
fy
the vacuum condition. Furthermore, we restrict ourselves t
o
a
class of
g
au
g
e transformation matrices which approach the identity matri
x
a
t infinity
(
i.e.
,
U
(
|
x
|
→
+
∞
)=
1
)
. It is well known that a three-dimensional
E
uclidean space with all the points at in
fi
nity bein
g
identi
fi
ed as the same one
i
sacutall
y
the three-sphere
S
3
.
On the other hand, the unitar
y
matrix U
(
x
)
d
efines the mapping from
S
3
into the parameter space of the grou
p
SU
(
2
),
which is also a three-sphere.
A
ccordin
g
to the homotopy theory, the
g
au
ge
transformation function
s
U
(
x
)
fall into different homotopic classes, which are
c
haracterized by the integer numbers defined in Eq.
(
11.19
)
. In a quantum
theor
y
there ma
y
exist transitions between two di
ff
erent vacuum states. T
o
c
alculate the tunneling probability at the zero temperature, one should find
out a solution to the field equations with finite energies
(
Belavin
et al.
,19
7
5;
’t Hooft, 1976
)
. For the transitions with
Δ
N
CS
NN
=
±
1
, the tunnelin
g
probabil-
i
ty is approximately given by e
−
4
π
/α
w
∼
1
0
−
1
61
w
ith
α
w
≡ g
2
/
(
4
π
)
, implyin
g
that the
B
-vio
l
atin
g
interactions are ne
gl
i
g
i
bl
ysma
ll
.
Notethatwehavei
g
nored two important issues in the above discussions
.
On the one hand, the baryon number asymmetry should be generated in the
ear
l
y Universe at extreme
l
y
h
i
gh
temperatures, so one must ta
k
e into accoun
t
the finite-temperature effects. On the other hand, the field confi
g
urations o
f
the vacua in the SM should include the Higgs boson field. In order for
a
transition between two di
ff
erent vacua to work, we have to examine whethe
r
there exists a static field configuration interpolating the two vacua
(
Manton,
1
983
)
. Such a solution, named
s
p
h
a
l
ero
n
a
tthetopofthepotentialbarrier,
h
as been
f
ound by solvin
g
the
fi
eld equations in the limit o
f
si
n
2
θ
w
→
0
(
Klinkhamer and Manton, 1984
)
. The energy of the sphaleron is given by
E
sp
h
=
4
π
v
g
B
λ
g
,
(
11.20
)
whe
r
e
v
a
n
d
λ
are the vacuum expectation value and the sel
f
-couplin
g
con-
s
tant o
f
the Hi
gg
s
fi
eld, respectively. Note that the
f
unction
B
(
x
)
is slowl
y
varying; e.g.,
B
(
0
)
1
.
5
2an
d
B
(
∞
)
2
.
7
2
(
Klinkhamer and Manton, 1984
).
In t
h
eear
l
y Universe, w
h
en t
h
e temperature was
h
i
gh
er t
h
an t
h
e potentia
l
barrier between the vacua, the transition should not be hi
g
hly suppressed.

1
1.2 Typical Mechanisms o
f
Baryogenesis 38
5
Includin
g
the
fi
nite-temperature corrections, the sphaleron ener
g
y turns out
to be
(
Brihaye and Kunz, 1992
)
E
sp
h
(
T
)
=
2
M
W
MM
(
T
)
α
w
B
λ
g
,
(
11.21
)
where th
e
W
-
boson mass
M
W
M
M
(
T
)
=
gv
(
T
)
/
2istem
p
erature-de
p
endent, so i
s
t
h
e vacuum expectation va
l
u
e
v
(
T
)
of the Higgs field. It is worth mentionin
g
t
h
at t
h
e
g
au
g
e symmetry, w
h
ic
h
is spontaneous
l
y
b
ro
k
en at t
h
e zero tempera
-
ture, can be restored at much higher temperatures
(
Weinberg, 1974; Kirzhnits
a
nd Linde, 1974; Dolan and Jackiw, 1974; Bernard, 1974
)
. Hence there must
be a transition
f
rom the symmetric phase to the symmetry-breakin
g
phas
e
a
sthetem
p
eratur
e
T decreases. During and below the phase transition, the
rate per unit volume for the sphaleron o
r
B
-vio
l
ating processes is estimate
d
to be
(
Carlson
et al.
,
1990; Dine
et al.
,
1992
)
γ
sp
h
∼
2
.
8
×
1
0
5
κT
4
α
w
4
π
4
E
sph
(
T
)
B
(
λ
/g
)
T
7
e
x
p
{
−
E
s
p
h
/T
}
,
(
11.22
)
w
h
ere 1
0
−
4
κ
10
−
1
.
Above the phase transition, one ha
s
v
(
T
)
= 0 and
t
h
us t
h
e rate per unit vo
l
ume approximates t
o
γ
sp
h
∼
κ
(
α
w
T
)
4
.
I
tca
n
be
s
hown that the s
p
haleron rate is in thermal e
q
uilibrium if the tem
p
erature
T
l
ies in t
h
e range 1
0
2
G
e
V
T
10
12
G
eV
(
Kuzmin
et al.
,
1985
).
Finall
y
, let us examine how
C
P violation in the
S
M comes into pla
y
and
d
iscuss
p
ossible im
p
lications of the de
p
arture from thermal e
q
uilibrium.
A
c
rucia
l
perio
dh
ereist
h
ee
l
ectrowea
k
p
h
ase transition, w
h
ic
h
is governe
dby
the e
ff
ective potential
V
eff
VV
(
H
,
T
)
of the system
(
Weinberg, 1974
)
.Atahig
h
tem
p
erature the minimum of
V
eff
VV
(
H,
T
)
is reached at
H
=
0, indicating tha
t
the
g
au
g
e symmetry is preserved. For the
fi
rst-order phase transition, another
loca
lm
a
xim
u
m
a
n
d
minim
u
m
of
V
eff
VV
(
H, T
)
appear a
t
H
max
a
n
d
H
min
,
a
sthetem
p
eratur
e
T decreases. Note tha
t
H
ma
x
<
H
min
,
and the secon
d
m
inimum
b
ecomes
d
e
g
enerate wit
h
t
h
eori
g
ina
l
one at t
h
ecritica
l
tempera
-
tu
r
e
T
=
T
c
T
T
(
i.e.,
V
eff
VV
(
0
,T
c
T
T
)=
V
eff
VV
(
H
m
i
n
,T
c
T
T
)
holds
)
.Atthismomentthere
a
re two
d
egenerate vacua: one is a
t
H
=0,w
h
ere t
h
e gauge symmetry is
m
aintaine
d
;an
d
t
h
eot
h
er is a
t
H
m
i
n
,
w
h
ere t
h
e
g
au
g
e symmetry is
b
ro
k
en
.
Therefore, a transition from the symmetric phase to the symmetry-breakin
g
phase takes place by tunneling the potential barrier between them. If the tem
-
perature
d
rops
b
e
l
o
w
T
c
TT
, the second local minimum o
f
V
eff
VV
(
H, T
)
becomes th
e
g
lobal one. This first-order phase transition starts with the small bubbles in-
s
ide which the symmetry is broken
(
i.e.,
v
(
T
)=
H
= 0), but outside is the
sy
mmetric p
h
ase wit
h
v
(
T
)
=0.As
T
d
ecreases, t
h
e
b
u
bbl
es expan
d
an
d
c
ollide, and finall
y
fill up the whole Universe. When the wall of the bubble
expan
d
soutwar
d
s, t
h
eor
d
er paramete
r
v
(
T
)
changes dramatically from zer
o
to a nonzero value which induces the departure
f
rom thermal equilibrium.
O
n
the other hand, the bar
y
on numbers carried b
y
quark and antiquark fields
