Wooldridge - Introductory Econometrics - A Modern Approach, 2e
Подождите немного. Документ загружается.

(i) What kinds of factors are contained in u? Are these likely to be corre-
lated with level of education?
(ii) Will a simple regression analysis uncover the ceteris paribus effect of
education on fertility? Explain.
2.2 In the simple linear regression model y
0
1
x u, suppose that E(u) 0.
Letting
0
E(u), show that the model can always be rewritten with the same slope,
but a new intercept and error, where the new error has a zero expected value.
2.3 The following table contains the ACT scores and the GPA (grade point average)
for 8 college students. Grade point average is based on a four-point scale and has been
rounded to one digit after the decimal.
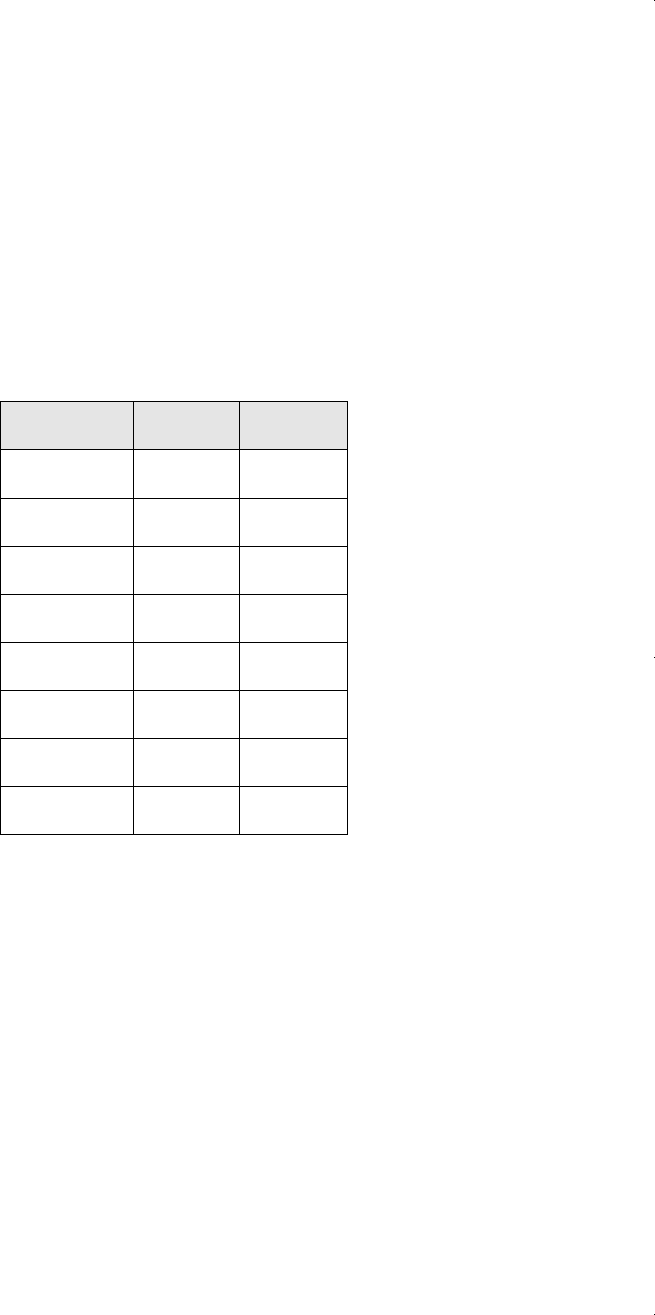
Student GPA ACT
1 2.8 21
2 3.4 24
3 3.0 26
4 3.5 27
5 3.6 29
6 3.0 25
7 2.7 25
8 3.7 30
(i) Estimate the relationship between GPA and ACT using OLS; that is,
obtain the intercept and slope estimates in the equation
GP
ˆ
A
ˆ
0
ˆ
1
ACT.
Comment on the direction of the relationship. Does the intercept have a
useful interpretation here? Explain. How much higher is the GPA pre-
dicted to be, if the ACT score is increased by 5 points?
(ii) Compute the fitted values and residuals for each observation and verify
that the residuals (approximately) sum to zero.
(iii) What is the predicted value of GPA when ACT 20?
(iv) How much of the variation in GPA for these 8 students is explained by
ACT? Explain.
2.4 The data set BWGHT.RAW contains data on births to women in the United States.
Two variables of interest are the dependent variable, infant birth weight in ounces
(bwght), and an explanatory variable, average number of cigarettes the mother smoked
Chapter 2 The Simple Regression Model
61
d 7/14/99 4:31 PM Page 61
per day during pregnancy (cigs). The following simple regression was estimated using
data on n 1388 births:
bwgˆht 119.77 0.514 cigs
(i) What is the predicted birth weight when cigs 0? What about when
cigs 20 (one pack per day)? Comment on the difference.
(ii) Does this simple regression necessarily capture a causal relationship
between the child’s birth weight and the mother’s smoking habits?
Explain.
2.5 In the linear consumption function
coˆns
ˆ
0
ˆ
1
inc,
the (estimated) marginal propensity to consume (MPC) out of income is simply the
slope,
ˆ
1
, while the average propensity to consume (APC) is coˆns/inc
ˆ
0
/inc
ˆ
1
.
Using observations for 100 families on annual income and consumption (both measured
in dollars), the following equation is obtained:
coˆns 124.84 0.853 inc
n 100, R
2
0.692
(i) Interpret the intercept in this equation and comment on its sign and
magnitude.
(ii) What is predicted consumption when family income is $30,000?
(iii) With inc on the x-axis, draw a graph of the estimated MPC and APC.
2.6 Using data from 1988 for houses sold in Andover, MA, from Kiel and McClain
(1995), the following equation relates housing price (price) to the distance from a
recently built garbage incinerator (dist):
log(prˆice) 9.40 0.312 log(dist)
n 135, R
2
0.162
(i) Interpret the coefficient on log(dist). Is the sign of this estimate what
you expect it to be?
(ii) Do you think simple regression provides an unbiased estimator of the
ceteris paribus elasticity of price with respect to dist? (Think about the
city’s decision on where to put the incinerator.)
(iii) What other factors about a house affect its price? Might these be corre-
lated with distance from the incinerator?
2.7 Consider the savings function
sav
0
1
inc u, u 兹inc
—
e,
where e is a random variable with E(e) 0 and Var(e)
e
2
. Assume that e is inde-
pendent of inc.
(i) Show that E(u兩inc) 0, so that the key zero conditional mean assump-
tion (Assumption SLR.3) is satisfied. [Hint: If e is independent of inc,
then E(e兩inc) E(e).]
Part 1 Regression Analysis with Cross-Sectional Data
62
d 7/14/99 4:31 PM Page 62

(ii) Show that Var(u兩inc)
e
2
inc, so that the homoskedasticity Assumption
SLR.5 is violated. In particular, the variance of sav increases with inc.
[Hint: Var(e兩inc) Var(e), if e and inc are independent.]
(iii) Provide a discussion that supports the assumption that the variance of
savings increases with family income.
2.8 Consider the standard simple regression model y
0
1
x u under
Assumptions SLR.1 through SLR.4. Thus, the usual OLS estimators
ˆ
0
and
ˆ
1
are unbi-
ased for their respective population parameters. Let
˜
1
be the estimator of
1
obtained
by assuming the intercept is zero (see Section 2.6).
(i) Find E(
˜
1
) in terms of the x
i
,
0
, and
1
. Verify that
˜
1
is unbiased for
1
when the population intercept (
0
) is zero. Are there other cases
where
˜
1
is unbiased?
(ii) Find the variance of
˜
1
.(Hint: The variance does not depend on
0
.)
(iii) Show that Var(
˜
1
) Var(
ˆ
1
). [Hint: For any sample of data,
兺
n
i1
x
i
2
兺
n
i1
(x
i
x¯)
2
, with strict inequality unless x¯ 0.]
(iv) Comment on the tradeoff between bias and variance when choosing
between
ˆ
1
and
˜
1
.
2.9 (i) Let
ˆ
0
and
ˆ
1
be the intercept and slope from the regression of y
i
on x
i
, using n
observations. Let c
1
and c
2
, with c
2
0, be constants. Let
˜
0
and
˜
1
be the intercept and
slope from the regression c
1
y
i
on c
2
x
i
. Show that
˜
1
(c
1
/c
2
)
ˆ
1
and
˜
0
c
1
ˆ
0
, thereby
verifying the claims on units of measurement in Section 2.4. [Hint: To obtain
˜
1
, plug
the scaled versions of x and y into (2.19). Then, use (2.17) for
˜
0
, being sure to plug in
the scaled x and y and the correct slope.]
(ii) Now let
˜
0
and
˜
1
be from the regression (c
1
y
i
) on (c
2
x
i
) (with no
restriction on c
1
or c
2
). Show that
˜
1
ˆ
1
and
˜
0
ˆ
0
c
1
c
2
ˆ
1
.
COMPUTER EXERCISES
2.10 The data in 401K.RAW are a subset of data analyzed by Papke (1995) to study the
relationship between participation in a 401(k) pension plan and the generosity of the
plan. The variable prate is the percentage of eligible workers with an active account;
this is the variable we would like to explain. The measure of generosity is the plan
match rate, mrate. This variable gives the average amount the firm contributes to each
worker’s plan for each $1 contribution by the worker. For example, if mrate 0.50,
then a $1 contribution by the worker is matched by a 50¢ contribution by the firm.
(i) Find the average participation rate and the average match rate in the
sample of plans.
(ii) Now estimate the simple regression equation
praˆte
ˆ
0
ˆ
1
mrate,
and report the results along with the sample size and R-squared.
(iii) Interpret the intercept in your equation. Interpret the coefficient on mrate.
(iv) Find the predicted prate when mrate 3.5. Is this a reasonable predic-
tion? Explain what is happening here.
Chapter 2 The Simple Regression Model
63
d 7/14/99 4:31 PM Page 63
(v) How much of the variation in prate is explained by mrate? Is this a lot
in your opinion?
2.11 The data set in CEOSAL2.RAW contains information on chief executive officers
for U.S. corporations. The variable salary is annual compensation, in thousands of dol-
lars, and ceoten is prior number of years as company CEO.
(i) Find the average salary and the average tenure in the sample.
(ii) How many CEOs are in their first year as CEO (that is, ceoten 0)?
What is the longest tenure as a CEO?
(iii) Estimate the simple regression model
log(salary)
0
1
ceoten u,
and report your results in the usual form. What is the (approximate) pre-
dicted percentage increase in salary given one more year as a CEO?
2.12 Use the data in SLEEP75.RAW from Biddle and Hamermesh (1990) to study whether
there is a tradeoff between the time spent sleeping per week and the time spent in paid
work. We could use either variable as the dependent variable. For concreteness, estimate
the model
sleep
0
1
totwrk u,
where sleep is minutes spent sleeping at night per week and totwrk is total minutes
worked during the week.
(i) Report your results in equation form along with the number of obser-
vations and R
2
. What does the intercept in this equation mean?
(ii) If totwrk increases by 2 hours, by how much is sleep estimated to fall?
Do you find this to be a large effect?
2.13 Use the data in WAGE2.RAW to estimate a simple regression explaining monthly
salary (wage) in terms of IQ score (IQ).
(i) Find the average salary and average IQ in the sample. What is the stan-
dard deviation of IQ? (IQ scores are standardized so that the average in
the population is 100 with a standard deviation equal to 15.)
(ii) Estimate a simple regression model where a one-point increase in IQ
changes wage by a constant dollar amount. Use this model to find the
predicted increase in wage for an increase in IQ of 15 points. Does IQ
explain most of the variation in wage?
(iii) Now estimate a model where each one-point increase in IQ has the
same percentage effect on wage. If IQ increases by 15 points, what is
the approximate percentage increase in predicted wage?
2.14 For the population of firms in the chemical industry, let rd denote annual expen-
ditures on research and development, and let sales denote annual sales (both are in mil-
lions of dollars).
(i) Write down a model (not an estimated equation) that implies a constant
elasticity between rd and sales. Which parameter is the elasticity?
(ii) Now estimate the model using the data in RDCHEM.RAW. Write out the
estimated equation in the usual form. What is the estimated elasticity of
rd with respect to sales? Explain in words what this elasticity means.
Part 1 Regression Analysis with Cross-Sectional Data
64
d 7/14/99 4:31 PM Page 64

APPENDIX 2A
Minimizing the Sum of Squared Residuals
We show that the OLS estimates
ˆ
0
and
ˆ
1
do minimize the sum of squared residuals,
as asserted in Section 2.2. Formally, the problem is to characterize the solutions
ˆ
0
and
ˆ
1
to the minimization problem
min
b
0
,b
1
兺
n
i1
(y
i
b
0
b
1
x
i
)
2
,
where b
0
and b
1
are the dummy arguments for the optimization problem; for simplicity,
call this function Q(b
0
,b
1
). By a fundamental result from multivariable calculus (see
Appendix A), a necessary condition for
ˆ
0
and
ˆ
1
to solve the minimization problem is
that the partial derivatives of Q(b
0
,b
1
) with respect to b
0
and b
1
must be zero when eval-
uated at
ˆ
0
,
ˆ
1
: Q(
ˆ
0
,
ˆ
1
)/b
0
0 and Q(
ˆ
0
,
ˆ
1
)/b
1
0. Using the chain rule from
calculus, these two equations become
2
兺
n
i1
(y
i
ˆ
0
ˆ
1
x
i
) 0.
2
兺
n
i1
x
i
(y
i
ˆ
0
ˆ
1
x
i
) 0.
These two equations are just (2.14) and (2.15) multiplied by 2n and, therefore, are
solved by the same
ˆ
0
and
ˆ
1
.
How do we know that we have actually minimized the sum of squared residuals?
The first order conditions are necessary but not sufficient conditions. One way to veri-
fy that we have minimized the sum of squared residuals is to write, for any b
0
and b
1
,
Q(b
0
,b
1
)
兺
n
i1
(y
i
ˆ
0
ˆ
1
x
i
(
ˆ
0
b
0
) (
ˆ
1
b
1
)x
i
)
2
兺
n
i1
(uˆ
i
(
ˆ
0
b
0
) (
ˆ
1
b
1
)x
i
)
2
兺
n
i1
uˆ
i
2
n(
ˆ
0
b
0
)
2
(
ˆ
1
b
1
)
2
兺
n
i1
x
i
2
2(
ˆ
0
b
0
)(
ˆ
1
b
1
)
兺
n
i1
x
i
,
where we have used equations (2.30) and (2.31). The sum of squared residuals does not
depend on b
0
or b
1
, while the sum of the last three terms can be written as
兺
n
i1
[(
ˆ
0
b
0
) (
ˆ
1
b
1
)x
i
]
2
,
as can be verified by straightforward algebra. Because this is a sum of squared terms,
it can be at most zero. Therefore, it is smallest when b
0
=
ˆ
0
and b
1
=
ˆ
1
.
Chapter 2 The Simple Regression Model
65
d 7/14/99 4:31 PM Page 65

I
n Chapter 2, we learned how to use simple regression analysis to explain a depen-
dent variable, y, as a function of a single independent variable, x. The primary draw-
back in using simple regression analysis for empirical work is that it is very diffi-
cult to draw ceteris paribus conclusions about how x affects y: the key assumption,
SLR.3—that all other factors affecting y are uncorrelated with x—is often unrealistic.
Multiple regression analysis is more amenable to ceteris paribus analysis because it
allows us to explicitly control for many other factors which simultaneously affect the
dependent variable. This is important both for testing economic theories and for evaluat-
ing policy effects when we must rely on nonexperimental data. Because multiple regres-
sion models can accommodate many explanatory variables that may be correlated, we can
hope to infer causality in cases where simple regression analysis would be misleading.
Naturally, if we add more factors to our model that are useful for explaining y, then
more of the variation in y can be explained. Thus, multiple regression analysis can be
used to build better models for predicting the dependent variable.
An additional advantage of multiple regression analysis is that it can incorporate
fairly general functional form relationships. In the simple regression model, only one
function of a single explanatory variable can appear in the equation. As we will see, the
multiple regression model allows for much more flexibility.
Section 3.1 formally introduces the multiple regression model and further dis-
cusses the advantages of multiple regression over simple regression. In Section 3.2, we
demonstrate how to estimate the parameters in the multiple regression model using the
method of ordinary least squares. In Sections 3.3, 3.4, and 3.5, we describe various sta-
tistical properties of the OLS estimators, including unbiasedness and efficiency.
The multiple regression model is still the most widely used vehicle for empirical
analysis in economics and other social sciences. Likewise, the method of ordinary least
squares is popularly used for estimating the parameters of the multiple regression model.
3.1 MOTIVATION FOR MULTIPLE REGRESSION
The Model with Two Independent Variables
We begin with some simple examples to show how multiple regression analysis can be
used to solve problems that cannot be solved by simple regression.
66
Chapter Three
Multiple Regression Analysis:
Estimation
d 7/14/99 4:55 PM Page 66

The first example is a simple variation of the wage equation introduced in Chapter
2 for obtaining the effect of education on hourly wage:
wage
0
1
educ
2
exper u,
(3.1)
where exper is years of labor market experience. Thus, wage is determined by the two
explanatory or independent variables, education and experience, and by other unob-
served factors, which are contained in u. We are still primarily interested in the effect
of educ on wage, holding fixed all other factors affecting wage; that is, we are interest-
ed in the parameter
1
.
Compared with a simple regression analysis relating wage to educ, equation (3.1)
effectively takes exper out of the error term and puts it explicitly in the equation.
Because exper appears in the equation, its coefficient,
2
, measures the ceteris paribus
effect of exper on wage, which is also of some interest.
Not surprisingly, just as with simple regression, we will have to make assumptions
about how u in (3.1) is related to the independent variables, educ and exper. However,
as we will see in Section 3.2, there is one thing of which we can be confident: since
(3.1) contains experience explicitly, we will be able to measure the effect of education
on wage, holding experience fixed. In a simple regression analysis—which puts exper
in the error term—we would have to assume that experience is uncorrelated with edu-
cation, a tenuous assumption.
As a second example, consider the problem of explaining the effect of per student
spending (expend) on the average standardized test score (avgscore) at the high school
level. Suppose that the average test score depends on funding, average family income
(avginc), and other unobservables:
avgscore
0
1
expend
2
avginc u.
(3.2)
The coefficient of interest for policy purposes is
1
, the ceteris paribus effect of expend
on avgscore. By including avginc explicitly in the model, we are able to control for its
effect on avgscore. This is likely to be important because average family income tends
to be correlated with per student spending: spending levels are often determined by both
property and local income taxes. In simple regression analysis, avginc would be in-
cluded in the error term, which would likely be correlated with expend, causing the
OLS estimator of
1
in the two-variable model to be biased.
In the two previous similar examples, we have shown how observable factors other
than the variable of primary interest [educ in equation (3.1), expend in equation (3.2)]
can be included in a regression model. Generally, we can write a model with two inde-
pendent variables as
y
0
1
x
1
2
x
2
u,
(3.3)
where
0
is the intercept,
1
measures the change in y with respect to x
1
, holding other
factors fixed, and
2
measures the change in y with respect to x
2
, holding other factors
fixed.
Chapter 3 Multiple Regression Analysis: Estimation
67
d 7/14/99 4:55 PM Page 67

Multiple regression analysis is also useful for generalizing functional relationships
between variables. As an example, suppose family consumption (cons) is a quadratic
function of family income (inc):
cons
0
1
inc
2
inc
2
u,
(3.4)
where u contains other factors affecting consumption. In this model, consumption
depends on only one observed factor, income; so it might seem that it can be handled
in a simple regression framework. But the model falls outside simple regression
because it contains two functions of income, inc and inc
2
(and therefore three parame-
ters,
0
,
1
, and
2
). Nevertheless, the consumption function is easily written as a
regression model with two independent variables by letting x
1
inc and x
2
inc
2
.
Mechanically, there will be no difference in using the method of ordinary least
squares (introduced in Section 3.2) to estimate equations as different as (3.1) and (3.4).
Each equation can be written as (3.3), which is all that matters for computation. There
is, however, an important difference in how one interprets the parameters. In equation
(3.1),
1
is the ceteris paribus effect of educ on wage. The parameter
1
has no such
interpretation in (3.4). In other words, it makes no sense to measure the effect of inc on
cons while holding inc
2
fixed, because if inc changes, then so must inc
2
! Instead, the
change in consumption with respect to the change in income—the marginal propen-
sity to consume—is approximated by
⬇
1
2
2
inc.
See Appendix A for the calculus needed to derive this equation. In other words, the mar-
ginal effect of income on consumption depends on
2
as well as on
1
and the level of
income. This example shows that, in any particular application, the definition of the
independent variables are crucial. But for the theoretical development of multiple
regression, we can be vague about such details. We will study examples like this more
completely in Chapter 6.
In the model with two independent variables, the key assumption about how u is
related to x
1
and x
2
is
E(u兩x
1
,x
2
) 0.
(3.5)
The interpretation of condition (3.5) is similar to the interpretation of Assumption
SLR.3 for simple regression analysis. It means that, for any values of x
1
and x
2
in the
population, the average unobservable is equal to zero. As with simple regression, the
important part of the assumption is that the expected value of u is the same for all com-
binations of x
1
and x
2
; that this common value is zero is no assumption at all as long as
the intercept
0
is included in the model (see Section 2.1).
How can we interpret the zero conditional mean assumption in the previous exam-
ples? In equation (3.1), the assumption is E(u兩educ,exper) 0. This implies that other
factors affecting wage are not related on average to educ and exper. Therefore, if we
think innate ability is part of u, then we will need average ability levels to be the same
across all combinations of education and experience in the working population. This
cons
inc
Part 1 Regression Analysis with Cross-Sectional Data
68
d 7/14/99 4:55 PM Page 68

may or may not be true, but, as we will see in Section 3.3, this is the question we need
to ask in order to determine whether the method of ordinary least squares produces
unbiased estimators.
The example measuring student performance [equation (3.2)] is similar to the wage
equation. The zero conditional mean assumption is E(u兩expend,avginc) 0, which
means that other factors affecting test scores—school or student characteristics—are,
on average, unrelated to per student fund-
ing and average family income.
When applied to the quadratic con-
sumption function in (3.4), the zero condi-
tional mean assumption has a slightly dif-
ferent interpretation. Written literally,
equation (3.5) becomes E(u兩inc,inc
2
) 0.
Since inc
2
is known when inc is known,
including inc
2
in the expectation is redun-
dant: E(u兩inc,inc
2
) 0 is the same as
E(u兩inc) 0. Nothing is wrong with putting inc
2
along with inc in the expectation when
stating the assumption, but E(u兩inc) 0 is more concise.
The Model with
k
Independent Variables
Once we are in the context of multiple regression, there is no need to stop with two
independent variables. Multiple regression analysis allows many observed factors to
affect y. In the wage example, we might also include amount of job training, years of
tenure with the current employer, measures of ability, and even demographic variables
like number of siblings or mother’s education. In the school funding example, addi-
tional variables might include measures of teacher quality and school size.
The general multiple linear regression model (also called the multiple regression
model) can be written in the population as
y
0
1
x
1
2
x
2
3
x
3
…
k
x
k
u, (3.6)
where
0
is the intercept,
1
is the parameter associated with x
1
,
2
is the parameter
associated with x
2
, and so on. Since there are k independent variables and an intercept,
equation (3.6) contains k 1 (unknown) population parameters. For shorthand pur-
poses, we will sometimes refer to the parameters other than the intercept as slope para-
meters, even though this is not always literally what they are. [See equation (3.4),
where neither
1
nor
2
is itself a slope, but together they determine the slope of the
relationship between consumption and income.]
The terminology for multiple regression is similar to that for simple regression and
is given in Table 3.1. Just as in simple regression, the variable u is the error term or
disturbance. It contains factors other than x
1
, x
2
,…,x
k
that affect y. No matter how
many explanatory variables we include in our model, there will always be factors we
cannot include, and these are collectively contained in u.
When applying the general multiple regression model, we must know how to inter-
pret the parameters. We will get plenty of practice now and in subsequent chapters, but
Chapter 3 Multiple Regression Analysis: Estimation
69
QUESTION 3.1
A simple model to explain city murder rates (murdrate) in terms of
the probability of conviction (prbconv) and average sentence length
(avgsen) is
murdrate
0
1
prbconv
2
avgsen u.
What are some factors contained in u? Do you think the key assum-
ption (3.5) is likely to hold?
d 7/14/99 4:55 PM Page 69

it is useful at this point to be reminded of some things we already know. Suppose that
CEO salary (salary) is related to firm sales and CEO tenure with the firm by
log(salary)
0
1
log(sales)
2
ceoten
3
ceoten
2
u. (3.7)
This fits into the multiple regression model (with k 3) by defining y log(salary),
x
1
log(sales), x
2
ceoten, and x
3
ceoten
2
. As we know from Chapter 2, the para-
meter
1
is the (ceteris paribus) elasticity of salary with respect to sales. If
3
0, then
100
2
is approximately the ceteris paribus percentage increase in salary when ceoten
increases by one year. When
3
0, the effect of ceoten on salary is more compli-
cated. We will postpone a detailed treatment of general models with quadratics until
Chapter 6.
Equation (3.7) provides an important reminder about multiple regression analysis.
The term “linear” in multiple linear regression model means that equation (3.6) is lin-
ear in the parameters,
j
. Equation (3.7) is an example of a multiple regression model
that, while linear in the
j
, is a nonlinear relationship between salary and the variables
sales and ceoten. Many applications of multiple linear regression involve nonlinear
relationships among the underlying variables.
The key assumption for the general multiple regression model is easy to state in
terms of a conditional expectation:
E(u兩x
1
,x
2
,…,x
k
) 0. (3.8)
At a minimum, equation (3.8) requires that all factors in the unobserved error term be
uncorrelated with the explanatory variables. It also means that we have correctly
accounted for the functional relationships between the explained and explanatory vari-
ables. Any problem that allows u to be correlated with any of the independent variables
causes (3.8) to fail. In Section 3.3, we will show that assumption (3.8) implies that OLS
is unbiased and will derive the bias that arises when a key variable has been omitted
Part 1 Regression Analysis with Cross-Sectional Data
70
Table 3.1
Terminology for Multiple Regression
yx
1
, x
2
, …, x
k
Dependent Variable Independent Variables
Explained Variable Explanatory Variables
Response Variable Control Variables
Predicted Variable Predictor Variables
Regressand Regressors
d 7/14/99 4:55 PM Page 70
