Wilkinson D.J. Stochastic Modelling for Systems Biology
Подождите немного. Документ загружается.


194
BEYOND THE GILLESPIE ALGORITHM
2. Calculate the hazards for the fast reactions.
3. Numerically integrate the CLE for the fast reactions from
t to t + t::.t to obtain a
"sample path" for the continuous variables over the interval
(t,
t +
~t].§
4. Using the time-dependent hazards for the slow reactions, decide whether or not a
slow reaction has happened in
(t,
t +
~t].
5.
If
no slow reaction has occurred, set t : = t +
~t
and update the continuous
variables to their proposed values at this time.
6.
If
one slow reaction has occurred, identify the time, t
1
and type, set t : =
h,
and
update the system to
t
1
(using the type
of
the discrete reaction and the appropriate
continuous state).
7.
If
more than one slow reaction has occurred, reduce
l::.t
and return to step
3.
8.
If
t <
Trnax•
return to step 2.
Here, steps 6 and 7 could (in principle) be replaced with 6 and
7.
Identify the time
and type
of
the first reaction and 'update accordingly.
The reason the algorithm is presented this way is that it is slow and difficult to
identify the times
of
slow reactions using numerical integration and solution meth-
ods, because the reaction hazards correspond to sample paths
of
unknown stochastic
processes. For this reason, Salis
& Kaznessis (2005a) use approximate numerical
techniques to estimate the reaction times that are more accurate
if
the time is first
narrowed down to a small interval where it is known that only this one reaction
occurs. Salis & Kaznessis (2005a) also present another algorithm (the ANRH algo-
rithm), which is faster but less accurate than the NRH, as it allows multiple slow
reactions to fire without affecting the fast reactions; again, see the paper for further
details.
The NRH and related algorithms that couple a Markov jump process with a Lange-
vin approximation are (in principle) very attractive
as
they are more accurate than the
ODE hybrid algorithms and are likely to scale-up to very large models much better
than the maximal timestep algorithm.
8.4.4 Discussion
There is a clear and pressing need for accurate stochastic simulation algorithms that
are much faster than the exact algorithms. Although the
"pure" approximate algo-
rithms are elegant and appealing, they fail to adequately cope with the common
problem
of
multiple reactions happening on differing time scales. This then moti-
vates the development
of
hybrid algorithms that can address exactly
fuis
issue using
a combination
of
exact and approximate techniques. Unfortunately, all three
of
the
hybrid algorithms presented (and there are other, related algorithms that have not
been explicitly covered here) are somewhat "crude" in terms
of
fueir statistical so-
phistication. The
ODE model is unsatisfactory
as
the jump in scale from discrete
§
Of
course the true sample path is a diffusion process, which cannot be obtained in its entirity, and this
is the main complication for algorithms
of
this type; see the text immediately following the algorithm
for further details.


196
BEYOND THE GILLESPIE ALGORITHM
single
software
object
can
be
attractive
in
the
context
of
modelling
complex
chemical
species where the potential number
of
distinct molecular
sp~cies
is vast, yet only a
small number are expected to be present during the course
of
a given simulation run.
8.5 Exercises
1. Read the original source papers for the various different algorithms discussed in
this chapter, and work through some simple examples by hand on paper to see
how they really work.
2.
Code up some
of
the algorithms and compare them for accuracy on some
of
the
example models from Chapter 7. This can be done by comparing sample means,
standard deviations, and full empirical probability distributions at a collection
of
time points, using data from many independent simulation runs; see Salis & Kaz-
nessis (2005a) for further details.
3. After tuning the different algorithms so that they have reasonable accuracy, com-
pare them for speed. Note that the algorithms discussed in this chapter are de-
signed to be efficient for large models with large numbers
of
species, reactions,
and molecules, so it should not be too surprising
if
the algorithms tum out to be
slower than Gillespie's direct method on small models.
4. Download some software packages that implement stochastic simulation using
algorithms other than the direct method, and compare them in terms
of
flexibility,
accuracy, and performance. Links to some appropriate software are given on this
book's website.
8.6 Further reading
The main source papers for this chapter are Gibson & Bruck
(2000), Gillespie (200 1
),
Gillespie & Petzold (2003), Gillespie (2000), Kiehl
et
al. (2004), Puchalka & Kierzek
(2004), Rao & Arkin (2003), Haseltine & Rawlings (2002), and Salis & Kaznessis
(2005a). All are required reading for a complete understanding
of
how the various
algorithms work. Also see Wilkinson
(2006) for a discussion
of
the issues involved
in coupling Markov jump and Langevin processes.


198
BAYESIAN INFERENCE AND MCMC
Note that the probabilities P
(X=
x!Hi)
are known as likelihoods, and are often
written
L(Hi; x ), as they tend to be regarded
as
a function
of
the
Hi
for given fixed
outcome
x.
Note, however, that the likelihood function does not represent a PMF for
the
Hi;
in particular, there is no reason to suppose.that it will sum
to
1.
This is how it all works for purely discrete problems, but some adaptation is re-
quired before it can be used with continuous or mixed problems. Let us first stay
with discrete outcome
X and consider a continuum
of
hypotheses represented by
a continuous parameter
8.
Our prior beliefs must now be represented by a density
function, traditionally written,
1r(8).
Taking the continuous limit in the usual
way,
Bayes Theorem becomes
1r(BIX
= x) =
1r(8)
P
(X=
x!B)
.
fe
P
(X=
xl8')
1r(B')d8'
In this case the likelihood function is L(B; x) = P
(X
=
x!B),
regarded
as
a function
of
8 for given fixed
X.
Again, note that the likelihood function is not a density fore,
as it does not integrate to
1.
Using this notation we can rewrite Bayes Theorem
as
7r(BIX
= x) = 7r(8)L(8;
x)
'
fe
1r(8')L(8';x)d8'
and this is the way it is usually written in the context
of
Bayesian statistics, though the
likelihood function
L(
8;
x) means slightly different things depending on the context.
Note that the integral on the bottom line
of
Bayes Theorem is not a function
of
8,
and so simply represents a constant
of
proportionality. Thus, we can rewrite Bayes
Theorem in the simpler form
1r(BIX
= x)
ex:
1r(8)L(B;x),
(9.1)
giving rise to the Bayesian mantra "the posterior is proportional
to
the prior times
the
likelihood."
Example
Suppose that for a particular gene in a particular cell, transcription events occur ac-
cording to a Poisson process with rate
8 per minute. Prior
to
carrying out an exper-
iment, a biological expert specifies his opinion regarding
()
in the fonn
of
a
r(
a,
b)
distribution (Section 3.11). Suppose that for our expert, a =
2,
b =
1.
Counts
of
the
n1.1mber
of
transcript events are gathered from n separate one-minute intervals
to
get

200
BAYESIAN
INFERENCE
AND
MCMC
"'
ci
U')
ci
.,.
ci
~
,
M
,
Cl)
I
c:
ci
"
I
Cl
N
ci
ci
0
ci
0 2 3
4
5
6
e
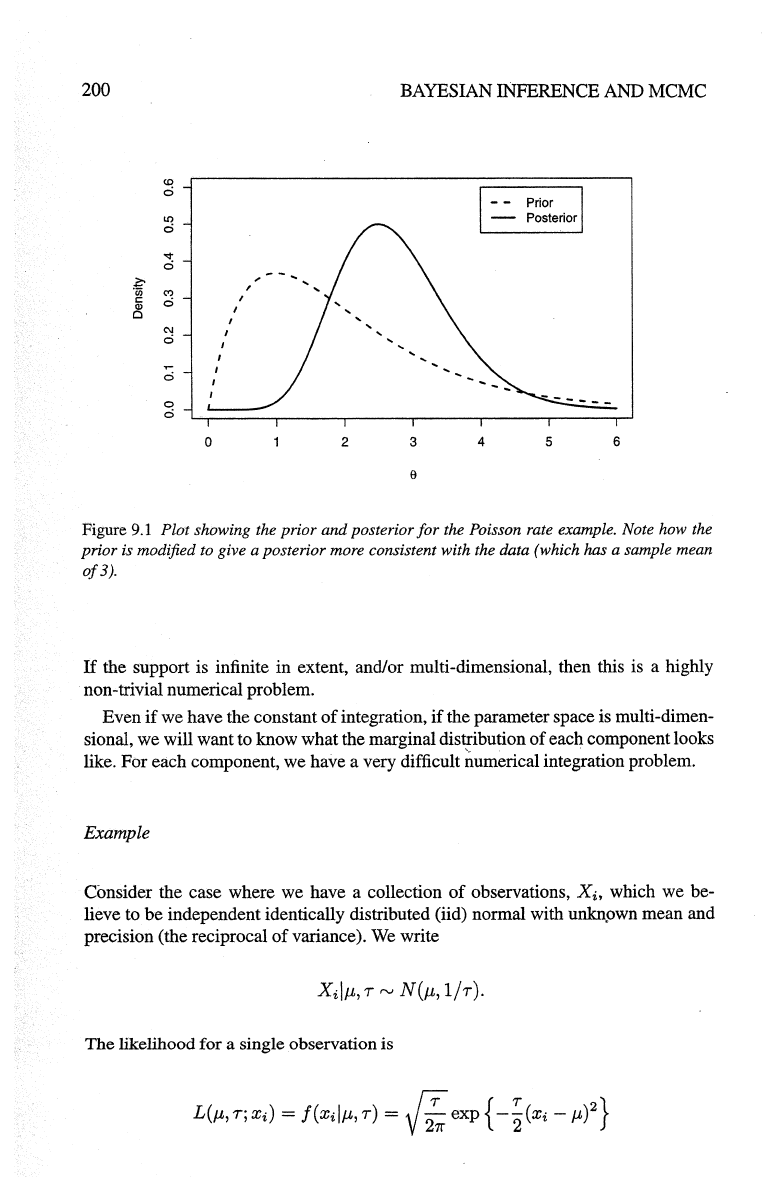
Figure
9.1
Plot showing the prior and posterior
for
the Poisson rate example. Note how the
prior is
modified to give a posterior more consistent with the data (which has a sample mean
of3).
If
the support is infinite in extent, and/or multi-dimensional, then this is a highly
non-trivial numerical problem.
Even
if
we have the constant
of
integration,
if
the parameter space is multi -dimen-
sional, we will want to know what the marginal distribution
of
each component looks
like. For each component, we have a very difficult
~umerical
integration problem.
Example
Consider the case where we have a collection
of
observations, Xi, which we be-
lieve to
be
independent identically distributed (iid) normal with unknpwn mean and
precision (the reciprocal
of
variance).
We
write
The
likelihood
for
a
single
observation
is


202
BAYESIAN INFERENCE AND MCMC
The posterior density for
JL
and 7 certainly will not factorise
(JL
and 7 are not in-
dependent
a posteriori), and will not even separate into the form
of
the conditional
normal-gamma conjugate form mentioned earlier.
So,
we
have the kernel
of
the posterior for
f.L
and
T,
but
it
is not in a standard form.
We can gain some idea
of
the likely values
of
(JL,
7) by plotting the bivariate surface
(the integration constant is not necessary for that), but we cannot work out the pos-
terior mean
or
variance,
or
the forms
of
the marginal posterior distributions for
JL
or
7,
since we cannot integrate out the other variable. We need a way
of
understand-
ing posterior densities which does not rely on being able to analytically integrate the
posterior density.
In fact, there is nothing particularly special about the fact that the density repre-
sents a Bayesian posterior. Given any complex non-standard multi-variate probability
distribution, we need ways to understand it, to calculate its moments, and to compute
its conditional and marginal distributions and their moments. Markov chain Monte
Carlo (MCMC) algorithms such as the Gibbs sampler and the Metropolis-Hastings
method provide a possible solution.
9.2 The Gibbs sampler
9.2.1 Introduction
The Gibbs sampler is a way
of
simulating from multi-variate distributions based only
on the ability to simulate from conditional distributions. In particular, it is appropriate
when sampling from marginal distributions is not convenient
or
possible.
Example
Reconsider the problem
of
Bayesian inference for the mean and variance
of
a nor-
mally distributed random sample.
In
particular, consider the non-conjugate approach
based on independent prior distributions for the mean and variance. The posterior
took the form
7r(JL,
7Jx)
<X
7a+.J}-l
exp
{
-~
[(n-
l)s
2
+
n(x-
JL)
2
]
-
~
(JL-
c)
2
-
b7}.
As explained previously, this distribution is not in a standard form. However, while
clearly not conjugate, this problem is often referred to as
semi-conjugate, because the
two
full conditional distributions
7r(JLJT,
x) and
1r(
7Jf.L,
x) are
of
standard form, and
further, are
of
the same form as the independent prior specifications. That is,
7JJL,
xis
gamma distributed and
f-LIT,
xis
normally distributed. In fact, by picking out terms in
the variable
of
interest and regarding everything else as a constant
of
proportionality,
we get

