White R.E. Computational Mathematics: Models, Methods, and Analysis with MATLAB and MPI
Подождите немного. Документ загружается.


4.6. HIGH PERFORMANCE COMPUTATIONS IN 3D 179
2. Modify solar3d.f90 to include the cases where
{, | and } do not
have to be equal.
3. Experiment with the geometric parameters
Z> K and O.
4. Experiment with the thermal parameters. What types of materials should
be used and how does this aect the cost?
5. Consider the derivative boundary condition on the top
gx
g}
= f(x
vxu
(w) x) for } = W=
Modify the above code to include this boundary condition. Experiment with
the constant f.
6. Calculate the change in heat content relative to the initial constant tem-
perature of 60.
7. Replace the cgssor3d() subroutine with a SOR subroutine and compare
the computing times. Use (4.5.8) and be careful to distinguish between the
time step index
n and the SOR index p=
8. Code the explicit method for the pass ive solar storage model, and observe
the stability constraint on the change in time. Compare the explicit and implicit
time discretizations for this problem.
4.6 High Performance Computations in 3D
4.6.1 Intro duction
Many applications are not only 3D problems, but they often have more than one
physical quantity associated with them. Two examples are aircraft modeling
and weather prediction. In the case of an aircraft, the lift forces are determined
by the velocity with three components, the pressure and in many cases the tem-
peratures. So, there are at least five quantities, which all vary with 3D space
and time. Weather forecasting models are much more complicated because
there are more 3D quantities, often one does not precisely know the bound-
ary conditions and there are chemical and physical changes in system. Such
problems require very complicated models, and faster algorithms and enhanced
computing hardware are essential to give realistic numerical simulations.
In this section reordering schemes such as coloring the nodes and domain
decomposition of the nodes will be introduced such that both direct and itera-
tive methods will have some independent calculation. This will allow the use of
be challenging, and this will be more carefully studied in the last four chapters.
4.6.2 Methods via Red-Black Reordering
One can reorder nodes so that the vector pip elines or multiprocessors can be
used to execute the SOR algorithm. First we do this for the 1D di
usion model
© 2004 by Chapman & Hall/CRC
high performance computers with vector pipelines (see Section 6.1) and multi-
processors (see Section 6.3). The implementation of these parallel methods can
180 CHAPTER 4. NONLINEAR AND 3D MODELS
with the unknown equal to zero at the boundary and
(Nx
{
)
{
= i({) (continuous model) (4.6.1)
N(x
l1
+ 2x
l
x
l+1
) = k
2
i(lk) (discrete model)= (4.6.2)
The SOR method requires input of
x
l1
and x
l+1
in order to compute the new
SOR value of
x
l
. Thus, if l is even, then only the x with odd subscripts are
required as input. The vector version of each SOR iteration is to group all the
even nodes and all the odd nodes: (i) use a vector pipe to do SOR over all the
odd nodes, (ii) update all
x for the odd nodes and (iii) use a vector pipe to do
SOR over all the even nodes. This is sometimes called red-black ordering.
The matrix version also indicates that this could be useful for direct meth-
ods. Suppose there are seven unknowns so that the classical order is
£
x
1
x
2
x
3
x
4
x
5
x
6
x
7
¤
W
=
The corresponding algebraic system is
5
9
9
9
9
9
9
9
9
7
2 1 0 0 0 0 0
1 2 1 0 0 0 0
0 1 2 1 0 0 0
0 0
1 2 1 0 0
0 0 0
1 2 1 0
0 0 0 0
1 2 1
0 0 0 0 0
1 2
6
:
:
:
:
:
:
:
:
8
5
9
9
9
9
9
9
9
9
7
x
1
x
2
x
3
x
4
x
5
x
6
x
7
6
:
:
:
:
:
:
:
:
8
= k
2
5
9
9
9
9
9
9
9
9
7
i
1
i
2
i
3
i
4
i
5
i
6
i
7
6
:
:
:
:
:
:
:
:
8
=
The red-black order is
£
x
1
x
3
x
5
x
7
x
2
x
4
x
6
¤
W
=
The reordered algebraic system is
5
9
9
9
9
9
9
9
9
7
2 0 0 0 1 0 0
0 2 0 0
1 1 0
0 0 2 0 0 1 1
0 0 0 2 0 0
1
1 1 0 0 2 0 0
0
1 1 0 0 2 0
0 0
1 1 0 0 2
6
:
:
:
:
:
:
:
:
8
5
9
9
9
9
9
9
9
9
7
x
1
x
3
x
5
x
7
x
2
x
4
x
6
6
:
:
:
:
:
:
:
:
8
= k
2
5
9
9
9
9
9
9
9
9
7
i
1
i
3
i
5
i
7
i
2
i
4
i
6
6
:
:
:
:
:
:
:
:
8
=
The coe!cient matrix for the red-black order is a block 2 × 2 matrix where
the block diagonal matrices are pointwise diagonal. Therefore, the solution by
to implement and has concurrent calculations.
Fortunately, the di
usion models for 2D and 3D will also have these desirable
attributes. The simplified discrete models for 2D and 3D are, respectively,
N(x
l1>m
x
l>m1
+ 4x
lm
x
l+1>m
x
l>m+1
) = k
2
i(lk> mk) and (4.6.3)
© 2004 by Chapman & Hall/CRC
block Gaussian elimination via the Schur complement, see Section 2.4, is easy
4.6. HIGH PERFORMANCE COMPUTATIONS IN 3D 181
N(x
l
1>m>o
x
l>m
1>o
x
l>m>o
1
+ 6x
lmo
x
l+1>m>o
x
l>m+1>o
x
l>m>o+1
)
=
k
2
i(lk> mk> ok)= (4.6.4)
In 2D di
usion the new values of x
lm
are functions of x
l+1>m
> x
l1>m
> x
l>m+1
and
x
l>m1
and so the SOR algorithm must be computed in a “checker board” order.
In the first grid row start with the
m = 1 and go in stride 2; for the second grid
row start with m = 2 and go in stride 2. Repeat this for all pairs of grid rows .
This will compute the newest
x
lm
for the same color, say, all the black nodes. In
order to do all the red nodes, repeat this, b ut now start with m = 2 in the first
grid row and then with m = 1 in the second grid row. Because the computation
of the newest
x
lm
requires input from the nodes of a dierent color, all the
calculations for the same color are independent. Therefore, the vector pipelines
or multiprocessors can be used.
Red-Black Order 2D SOR for (4.6.3).
choose nx, ny such that h = L/nx = W/ny
for m = 1,maxit
for j = 1,ny
index = mod(j,2)
for i = 2-index,nx,2
xwhps = (i(l k> m k) k k
+x(l 1> m) + x(l + 1> m)
+x(l> m 1) + x(l> m + 1)) =25
x(l> m) = (1 z) x(l> m) + z xwhps
endloop
endloop
for j = 1,ny
index = mod(j,2)
for i = 1+index,nx,2
xwhps = (i(l k> m k) k k
+x(l 1> m) + x(l + 1> m)
+
x
(l> m 1) + x(l> m + 1)) =25
x(l> m) = (1 z) x(l> m) + z xwhps
endloop
endloop
test for convergence
endloop.
For 3D di
usion the new values of x
lmo
are functions of x
l+1>m>o
> x
l1>m>o
>
x
l>m+1>o
> x
l>m1>o
> x
l>m>o+1
and x
l>m>o1
and so the SOR algorithm must be com-
puted in a “3D checker board” order. The first grid plane should have a 2D
checker board order, and then the next grid plane should have the interchanged
color 2D checker board order. Because the computation of the newest
x
lmo
re-
quires input from the nodes of a di
erent color, all the calculations for the same
color are independent. Therefore, the vector pipelines or multipro cessors can
be used.
© 2004 by Chapman & Hall/CRC
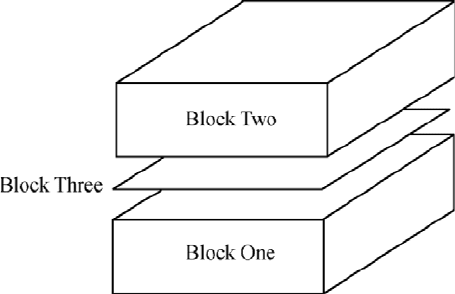
182 CHAPTER 4. NONLINEAR AND 3D MODELS
Figure 4.6.1: Domain Decompostion in 3D
4.6.3 Methods via Domain Decomposition Reordering
In order to introduce the domain decomposition order, again consider the 1D
problem in (4.6.2) and use seven unknowns. Here the domain decomposition
order is
£
x
1
x
2
x
3
x
5
x
6
x
7
x
4
¤
W
where the center no d e, x
4
, is listed last and the left and right blocks are listed
first and second. The algebraic system with this order is
5
9
9
9
9
9
9
9
9
7
2 1 0 0 0 0 0
1 2 1 0 0 0 0
0
1 2 0 0 0 1
0 0 0 2 1 0 1
0 0 0
1 2 1 0
0 0 0 0 1 2 0
0 0
1 1 0 0 2
6
:
:
:
:
:
:
:
:
8
5
9
9
9
9
9
9
9
9
7
x
1
x
2
x
3
x
5
x
6
x
7
x
4
6
:
:
:
:
:
:
:
:
8
= k
2
5
9
9
9
9
9
9
9
9
7
i
1
i
2
i
3
i
5
i
6
i
7
i
4
6
:
:
:
:
:
:
:
:
8
=
Domain decomposition ordering can also be used in 2D and 3D applications.
Consider the 3D case as depicted in Figure 4.6.1 where the nodes are partitioned
into two large blocks and a smaller third block separating the two large blocks
of nodes. Thus, if
lmo is in block 1 (or 2), then only input from block 1 (or 2)
and block 3 will be required to do the SOR computation. This suggests that
one can reorder the nodes so that disjoint blocks of nodes, which are separated
by a plane of nodes, can be computed concurrently in the SOR algorithm.
© 2004 by Chapman & Hall/CRC
4.6. HIGH PERFORMANCE COMPUTATIONS IN 3D 183
Domain Decomposition and 3D SOR Algorithm for (4.6.4).
define blocks 1, 2 and 3
for m = 1,maxit
concurrently do SOR on blo cks 1 and 2
update u
do SOR on block 3
test for convergence
endloop.
Domain decomposition order can also be used to directly solve for the u n-
knowns. This was initially described in Section 2.4 where the Schur complement
was studied. If the interface block 3 for the Poisson problem is listed last, then
the algebraic system has the form
5
7
D
11
0 D
13
0 D
22
D
23
D
31
D
32
D
33
6
8
5
7
X
1
X
2
X
3
6
8
=
5
7
I
1
I
2
I
3
6
8
=
(4.6.5)
In the Schur complement study in Section 2.4
E is the 2 × 2 block given by
D
11
and D
22
, and F is D
33
. Therefore, all the solves with E can be done
concurrently, in this case with two processors. By partitioning the space domain
into more blocks one can take advantage of additional processors. In the 3D
case the big block solves will be smaller 3D subproblems and here one may need
to use iterative methods. Note the conjugate gradient algorithm has a number
of vector updates, dot products and matrix-vector products, and all these steps
have independent parts.
In order to be more precise about the above, write the above 3 × 3 block
matrix equation in block component form
D
11
X
1
+ D
13
X
3
= I
1
> (4.6.6)
D
22
X
2
+ D
23
X
3
= I
2
and (4.6.7)
D
31
X
1
+ D
32
X
2
+ D
33
X
3
= I
3
= (4.6.8)
Now solve (4.6.6) and (4.6.7) for
X
1
and X
2
, and note the computations for
D
1
11
D
13
, D
1
11
I
1
, D
1
22
D
23
, and D
1
22
I
2
can be done concurrently. Put X
1
and
X
2
into (4.6.8) and solve for X
3
b
D
33
X
3
=
b
I
3
where
b
D
33
= D
33
D
31
D
1
11
D
13
D
32
D
1
22
D
23
and
b
I
3
= I
3
D
31
D
1
11
I
1
D
32
D
1
22
I
2
=
Then concurrently solve for X
1
= D
1
11
I
1
D
1
11
D
13
X
3
and X
2
= D
1
22
I
2
D
1
22
D
23
X
3
=
© 2004 by Chapman & Hall/CRC
184 CHAPTER 4. NONLINEAR AND 3D MODELS
4.6.4 Implementation of Gaussian Elimination via Domain
Decomposition
Consider the 2D steady state heat diusion problem. The MATLAB code
gedd.m is block Gaussian elimination where the
E matrix, in the 2 × 2 block
matrix of the Schur complement formulation, is a block diagonal matrix with
four blo cks on its diagonal. The
F = D
55
matrix is for the coe!cients of the
three interface grid rows between the four big blocks
5
9
9
9
9
7
D
11
0 0 0 D
15
0 D
22
0 0 D
25
0 0 D
33
0 D
35
0 0 0 D
44
D
45
D
W
15
D
W
12
D
W
13
D
W
14
D
55
6
:
:
:
:
8
5
9
9
9
9
7
X
1
X
2
X
3
X
4
X
5
6
:
:
:
:
8
=
5
9
9
9
9
7
I
1
I
2
I
3
I
4
I
5
6
:
:
:
:
8
=
(4.6.9)
In the M
ATLA B co de gedd.m the first 53 lines define the coe!cient matrix that
is associated with the 2D Poisson equation. The derivations of the steps for the
Schur complement calculations are similar to those with two big blocks. The
forward sweep to find the Schur complement matrix and right side is given in
lines 54-64 where parallel computations with four processors can be done. The
solution of the Schur complement reduced system is done in lines 66-69. The
parallel computations for the other four blocks of unknowns are done in lines
70-74.
MATLAB Code gedd.m
1. clear;
2. % Solves a block tridiagonal SPD algebraic system.
3. % Uses domain-decomposition and Schur complement.
4. % Define the block 5x5 matrix AAA
5. n = 5;
6. A = zeros(n);
7. for i = 1:n
8. A(i,i) = 4;
9. if (i
A1)
10. A(i,i-1)=-1;
11. end
12. if (i
?n)
13. A(i,i+1)=-1;
14. end
15. end
16. I = eye(n);
17. AA= zeros(n*n);
18. for i =1:n
19. newi = (i-1)*n +1;
20. lasti = i*n;
21. AA(newi:lasti,newi:lasti) = A;
© 2004 by Chapman & Hall/CRC
4.6. HIGH PERFORMANCE COMPUTATIONS IN 3D 185
22. if (i
A1)
23. AA(newi:lasti,newi-n:lasti-n) = -I;
24. end
25. if (i
?n)
26. AA(newi:lasti,newi+n:lasti+n) = -I;
27. end
28. end
29. Z = zeros(n);
30. A0 = [A Z Z;Z A Z;Z Z A];
31. A1 = zeros(n^2,3*n);
32. A1(n^2-n+1:n^2,1:n)=-I;
33. A2 = zeros(n^2,3*n);
34. A2(1:n,1:n) = -I;
35. A2(n^2-n+1:n^2,n+1:2*n) = -I;
36. A3 = zeros(n^2,3*n);
37. A3(1:n,n+1:2*n) = -I;
38. A3(n^2-n+1:n^2,2*n+1:3*n) = -I;
39. A4 = zeros(n^2,3*n);
40. A4(1:n,2*n+1:3*n) = -I;
41. ZZ =zeros(n^2);
42. AAA = [AA ZZ ZZ ZZ A1;
43. ZZ AA ZZ ZZ A2;
44. ZZ ZZ AA ZZ A3;
45. ZZ ZZ ZZ AA A4;
46. A1’ A2’ A3’ A4’ A0];
47. % Define the right side
48. d1 =ones(n*n,1)*10*(1/(n+1)^2);
49. d2 =ones(n*n,1)*10*(1/(n+1)^2);
50. d3 =ones(n*n,1)*10*(1/(n+1)^2);
51. d4 =ones(n*n,1)*10*(1/(n+1)^2);
52. d0 =ones(3*n,1)*10*(1/(n+1)^2);
53. d = [d1’ d2’ d3’ d4’ d0’]’;
54. % Start the Schur complement method
55. % Parallel computation with four processors
56. Z1 = AA\[A1 d1];
57. Z2 = AA\[A2 d2];
58. Z3 = AA\[A3 d3];
59. Z4 = AA\[A4 d4];
60. % Parallel computation with four processors
61. W1 = A1’*Z1;
62. W2 = A2’*Z2;
63. W3 = A3’*Z3;
64. W4 = A4’*Z4;
65. % Define the Schur complement system.
66. Ahat = A0 -W1(1:3*n,1:3*n) - W2(1:3*n,1:3*n)
© 2004 by Chapman & Hall/CRC

186 CHAPTER 4. NONLINEAR AND 3D MODELS
Figure 4.6.2: Domain Decomposition Matrix
- W3(1:3*n,1:3*n) -W4(1:3*n,1:3*n);
67. dhat = d0 -W1(1:3*n,1+3*n) -W2(1:3*n,1+3*n)
-W3(1:3*n,1+3*n) -W4(1:3*n,1+3*n);
68. % Solve the Schur complement system.
69. x0 = Ahat\dhat;
70. % Parallel computation with four processors
71. x1 = AA\(d1 - A1*x0);
72. x2 = AA\(d2 - A2*x0);
73. x3 = AA\(d3 - A3*x0);
74. x4 = AA\(d4 - A4*x0);
75. % Compare with the full Gauss elimination method.
76. norm(AAA\d - [x1;x2;x3;x4;x0])
Figure 4.6.2 is the coe
!cient matrix with the domain decomposition order-
ing. It was generated by the M
ATLA B file gedd.m and using the M ATL AB
command contour(AAA).
4.6.5 Exercises
1. In (4.6.5)-(4.6.8) list the interface block first and not last. Find the
solution with this new order.
2. Discuss the benefits of listing the interface blo ck first or last.
3. Consider the parallel solution of (4.6.9). Use the Schur complement as
in (4.6.5)-(4.6.8) to find the block matrix formula for the solution.
© 2004 by Chapman & Hall/CRC
4.6. HIGH PERFORMANCE COMPUTATIONS IN 3D 187
4. Use the results of the previous exercise to justify the lines 54-74 in the
M
ATLA B code gedd.m.
© 2004 by Chapman & Hall/CRC
Chapter 5
Epidemics, Images and
Money
This chapter contains nonlinear models of epidemics, image restoration and
value of option contracts. All three applications have di
usion-like terms, and
so mathematically they are similar to the models in the previous chapters. In
the epidemic model the unknown concentrations of the infected populations
will depend on both time and space. A good reference is the second edition
of A. Okubo and S. A. Levin [19]. Image restoration has applications to
satellite imaging, signal pro cessing and fish finders. The models are based on
minimization of suitable real valued functions whose gradients are similar to
the quasi-linear heat di
usion models. An excellent text with a number of
M
ATLA B codes has been written by C. R. Vogel [26]. The third application
is to the value of option contracts, which are agreements to sell or to buy
an item at a future date and given price. The option contract can itself be
sold and purchased, and the value of the option contract can be modeled by a
partial di
erential equation that is similar to the heat equation. The text by
P. Wilmott, S. Howison and J. Dewynne [28] presents a complete derivation of
this model as well as a self-contained discussion of the relevant mathematics,
numerical algorithms and related financial models.
5.1 Epidemics and Dispersion
5.1.1 Intro duction
In this section we study a variation of an epidemic model, which is similar to
measles. The population can be partitioned into three disjoint groups of sus-
ceptible, infected and recovered. One would like to precisely determine what
parameters control or prevent the epidemic. The classical time dependent model
has three ordinary di
erential equations. The mo dified model where the pop-
189
© 2004 by Chapman & Hall/CRC
