White R.E. Computational Mathematics: Models, Methods, and Analysis with MATLAB and MPI
Подождите немного. Документ загружается.

4.4. STEADY STATE 3D HEAT DIFFUSION 169
MATLAB Code sor3d.m
1. clear;
2. % This is the SOR solution of a 3D problem.
3. % Assume steady state heat di
usion.
4. % Given temperature on the boundary.
5. w = 1.8;
6. eps = .001;
7. maxit = 200;
8. nx = 20;
9. ny = 20;
10. nz = 20;
11. nunk = (nx-1)*(ny-1)*(nz-1);
12. u = 70.*ones(nx+1,ny+1,nz+1); % initial guess
13. u(1,:,:) = 200.; % hot boundary at x = 0
14. for iter = 1:maxit; % begin SOR
15. numi = 0;
16. for l = 2:nz
17. for j = 2:ny
18. for i = 2:nx
19. temp = u(i-1,j,l) + u(i,j-1,l) + u(i,j,l-1);
20. temp = (temp + u(i+1,j,l) + u(i,j+1,l)
+ u(i,j,l+1))/6.;
21. temp = (1. - w)*u(i,j,l) + w*temp;
22. error = abs(temp - u(i,j,l));
23. u(i,j,l) = temp;
24. if error
?eps
25. numi = numi + 1;
26. end
27. end
28. end
29. end
30. if numi==nunk
31. break
32. end
33. end
34. iter % iterations for convergence
35. slice(u, [5 10 15 20],10,10) % creates color coded 3D plot
36. colorbar
The SOR parameters
z = 1=6> 1=7 and 1.8 were used with the convergence
criteria
hsv = 0=001, and this resulted in convergence after 77, 50 and 62 itera-
tions, respectively.
temperatures inside the cooling fin. The lighter the shade of gray the warmer
the temperature. So, this figure indicates the fin is very cool to the left, and so
© 2004 by Chapman & Hall/CRC
In the Figure 4.4.2 theshades of gray indicate thevarying
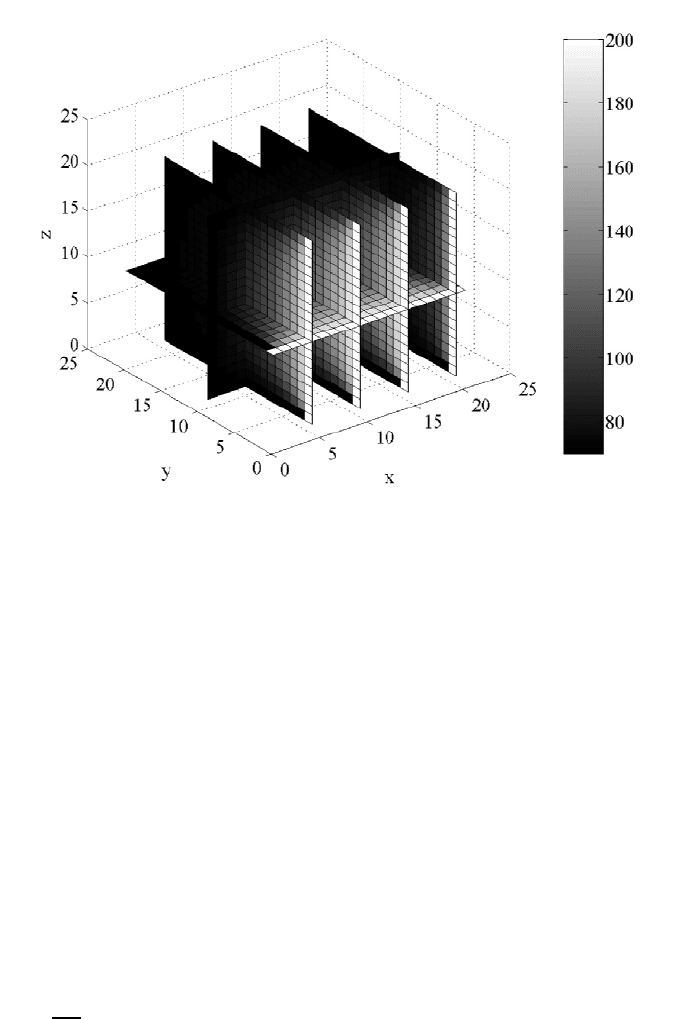
170 CHAPTER 4. NONLINEAR AND 3D MODELS
Figure 4.4.2: Temperatures Inside a 3D Fin
the fin for a hot boundary temperature equal to 200 is a little too long in the
| direction.
4.4.6 Assessment
The output from the 3D code gives variable temperatures in all three directions.
This indicates that a 1D or a 2D model is not applicable for this particular fin.
A possible problem with the present 3D model is the given b oundary condition
for the portion of the surface, which is between the fin and the surrounding
region. Here the alternative is a derivative boundary condition
N
gx
gq
= f(x
vxu
x) where q is the unit outward normal.
Both the surrounding temperature and the temperature of the transformer
could vary with time. Thus, this really is a time dependent problem, and
furthermore, one should consider the entire transformer and not just one fin.
4.4.7 Exercises
1. Use the MATLAB code sor3d.m and experiment with the slice command.
2. Experiment with di
erent numbers of unknowns q{> q| and q}, and de-
termine the best choices for the SOR parameter,
z.
3. Modify sor3d.m so that
{, | and } do not have to be equal.
© 2004 by Chapman & Hall/CRC
4.5. TIME DEPENDENT 3D DIFFUSION 171
Figure 4.5.1: Passive Solar Storage
4. Experiment with dierent O> Z and W . Determine when a 1D or 2D
model would be acceptable. Why is this important?
5. Modify sor3d.m to include the derivative boundary condition. Experi-
ment with the coe
!cient f as it ranges from 0 to infinity. For what values of f
will the given boundary condition be acceptable?
4.5 Time Dependent 3D Diusion
4.5.1 Intro duction
We consider a time dep endent 3D heat diusion model of a passive solar energy
storage unit similar to a concrete slab. The implicit time discretization method
will be used so as to avoid the stability constraint on the time step. This
generates a sequence of problems that are similar to the steady state 3D heat
equation, and the preconditioned conjugate gradient (PCG) algorithm will be
used to approximate the solutions of this sequence. Because of the size of the
problem Fortran 90 will be used to generate the sequence of 3D arrays for the
temperatures, and then M
ATLAB commands slice and mesh will be used to
dynamically visualize all this data
4.5.2 Applied Area
Consider a passive solar storage unit, which collects energy by the day and
gives it back at night. A simple example is a thick concrete floor in front of
windows, which face the sun during the day. Figure 4.5.1 depicts a concrete
slab with dimensions (0
> O) × (0> Z ) × (0> W ) where top } = W and the vertical
sides and bottom have given temperature. Assume there is di
usion in all three
directions. Since the surrounding temperature will vary with time, the amount
of heat that di
uses i n and out of the top will depend on time. The problem is
to determine the e
ectiveness of the passive unit as a function of its geometric
and thermal properties.
© 2004 by Chapman & Hall/CRC
172 CHAPTER 4. NONLINEAR AND 3D MODELS
4.5.3 Model
The model has the form of a time and space dependent partial dierential
equation. The empirical Fourier heat law again governs the di
usion. For the
nonsteady state problem we must consider the change in the amount of heat
energy that a mass can retain as a function of temperature. If the temperature
varies over a large range, or if there is a change in physical phase, then this
relationship is nonlinear. However, for small variations in the temperature the
change in heat for a small volume and small change in time is
f
s
(x({> |> }> w + w) x({> |> }> w)) (yroxph)
where
is the density, f
s
is the specific heat and x is the temperature. When
this is coupled with an internal heat source
i({> |> }> w) and diusion in three
directions for the
yroxph = {|}, we get
change in heat =
f
s
(x({> |> }> w + w) x({> |> }> w)){|}
i
({> |> }> w + w)({|})w
+(|})w(Nx
{
({ + {@2> |> }> w + w)
Nx
{
({ {@2> |> }> w + w))
+(
{})w(Nx
|
({> | + |@2> }> w + w)
Nx
|
({> | |@2> }> w + w))
+(
|{)w(Nx
}
({> |> } + }@2> w + w)
Nx
}
({> |> } }@2> w + w))= (4.5.1)
This approximation gets more accurate as
{, |, } and w go to zero.
So, divide by (
{|})w and let {, |, } and w go to zero. Since
(
x({> |> }> w + w) x({> |> }> w))@w converges to the time derivative of x, x
w
, as
w goes to zero, (4.5.1) gives the partial dierential equation in the 3D time
dep endent heat diusion model.
Time Dependent 3D Heat Di
usion.
f
s
x
w
= i({> |> }> w) + (Nx
{
({> |> }> w))
{
+
(
Nx
|
({> |> }> w))
|
+ (Nx
}
({> |> }> w))
}
(4.5.2)
x = 60 for } = 0, { = 0> O, | = 0> Z (4.5.3)
x = x
vxu
(w) = 60 + 30vlq(w@12) for } = W and (4.5.4)
x = 60 for w = 0= (4.5.5)
4.5.4 Method
The derivation of (4.5.1) suggests the implicit ti me discretization method. Let
n denote the time step with x
n
x({> |> }> nw). From the derivation of (4.5.2)
one gets a sequence of steady state problems
f
s
(x
n+1
x
n
)@w = i
n+1
+ (Nx
n+1
{
)
{
+
(
Nx
n+1
|
)
|
+ (Nx
n+1
{
)
|
= (4.5.6)
© 2004 by Chapman & Hall/CRC
4.5. TIME DEPENDENT 3D DIFFUSION 173
The space variables can be discretized just as in the steady state heat di
usion
problem. Thus, for each time step we must solve a linear algebraic system where
the right side changes from one time step to the next and equals
i
n+1
+f
s
x
n
@w
and the boundary condition (4.5.4) changes with time.
Implicit Time and Centered Finite Dierence Algorithm.
x
0
= x({> |> }> 0) from (4.5.5)
for k = 1, maxk
approximate the solution (4.5.6) by the finite di
erence method
use the appropriate boundary conditions in (4.5.3) and (4.5.4)
solve the resulting algebraic system such as in (4.5.8)
endloop.
This can be written as the seven point finite di
erence method, and here we
let
k = { = | = } and i({> |> }> w) = 0 so as to keep the code short. Use
the notation
x
n+1
lmo
x(lk> mk> ok> (n + 1)w) so that (4.5.6) is approximated by
f
s
(x
n+1
lmo
x
n
lmo
)@w = N@k
2
(6x
n+1
lmo
+x
n+1
l>m>o1
+ x
n+1
l>m1>o
+ x
n+1
l1>m>o
+x
n+1
l>m>o+1
+ x
n+1
l>m+1>o
+ x
n+1
l+1>m>o
)= (4.5.7)
Let
= (f
s
@w)@(N@k
2
) so that (4.5.7) simplifies to
(
+ 6)x
n+1
lmo
= x
n
lmo
+ x
n+1
l>m>o1
+ x
n+1
l>m1>o
+ x
n+1
l1>m>o
+ x
n+1
l>m>o+1
+ x
n+1
l>m+1>o
+ x
n+1
l+1>m>o
= (4.5.8)
4.5.5 Implementation
The Fortran 90 code solar3d.f90 is for time dependent heat transfer in a 3D
volume. It uses the implicit time discretization as simplified in (4.5.8). The
solve steps are done by the PCG with the SSOR preconditioner. The reader
should note how the third dimension and the nonzero boundary temperatures
are inserted into the code. The output is to the console with some information
about the PCG iteration and temperatures inside the volume. Also, some of
the temperatures are output to a file so that M
ATLAB’s command slice can be
used to produce a color coded 3D graph.
In solar3d.f90 the initialization is done in lines 1-22 where a 24 hour simu-
lation is done i n 48 time steps. The implicit time discretization is done in the
do loop given by lines 24-35. The function subroutine usur(t) in lines 38-43
is for the top boundary whose temperature changes with time. The subrou-
tine cgssor3d approximates the temperature at the next time step by using the
preconditioned conjugate gradient method with SSOR. The output is to the
console as well as to the file outsolar as indicated in lines 11 and 118-123. The
file outsolar is a 2D table where each row in the table corresponds to a partial
© 2004 by Chapman & Hall/CRC
174 CHAPTER 4. NONLINEAR AND 3D MODELS
grid row of every third temperature. So every 121 × 11 segment in the table
corresponds to the 3D temperatures for a single time.
Some of the other M
AT LAB codes also have Fortran versions so that the
interested reader can gradually learn the rudiments of Fortran 90. These include
heatl.f90, sor2d.f90, por2d.f90, newton.f90 and picpcg.f90.
Fortran Code solar3d.f90
1. program solar3d
2. ! This program solves
density csp ut -(Kux)x-(Kuy)y-(Kuz)z = f.
3. ! The thermal properties density, csp and K are constant.
4. ! The implicit time discretization is used.
5. ! The solve step is done in the subroutine cgssor3d.
6. ! It uses the PCG method with the SSOR preconditioner.
7. implicit none
8. real,dimension(0:30,0:30,0:30):: u,up
9. real :: dt,h,cond,density,csp,ac,time,ftime
10. integer :: i,j,n,l,m,mtime,mpcg
11. open(6,file=’c:\M
ATLAB6p5\work\outsolar’)
12. mtime = 48
13. ftime = 24.
14. ! Define the initial condition.
15. up = 60.0
16. n = 30
17. h = 1./n
18. cond = 0.81
19. density = 119.
20. csp = .21
21. dt = ftime/mtime
22. ac = density*csp*h*h/(cond*dt)
23. ! Start the time iteration.
24. do m=1,mtime
25. time = m*dt
26. !
27. ! The solve step is done by PCG with SSOR preconditioner.
28. !
29. call cgssor3d(ac,up,u,mp cg,n,time)
30. !
31. up =u
32. print*,"Time = ",time
33. print*," Number of PCG iterations = ",mpcg
34. print*," Max u = ", maxval(u)
35. end do
36. close(6)
37. end program
© 2004 by Chapman & Hall/CRC
4.5. TIME DEPENDENT 3D DIFFUSION 175
38. ! Heat source function for top.
39. function usur(t) result(fusur)
40. implicit none
41. real :: t,fusur
42. fusur = 60. + 30.*sin(t*3.14/12.)
43. end function
44. ! PCG subroutine.
45. subroutine cgssor3d(ac,up,u,mpcg,n,time)
46. implicit none
47. real,dimension(0:30,0:30,0:30):: p,q,r,rhat
48. real,dimension(0:30,0:30,0:30),intent(in):: up
49. real,dimension(0:30,0:30,0:30),intent(out):: u
50. real :: oldrho, rho,alpha,error,w,ra,usur
51. real ,intent(in):: ac,time
52. integer :: i,j,l,m
53. integer, intent(out):: mpcg
54. integer, intent(in):: n
55. w = 1.5
56. ra = 1./(6.+ac)
57. r = 0.0
58. rhat = 0.0
59. q = 0.0
60. p = 0.0
61. r = 0.0
62. ! Uses previous temp erature as an initial guess.
63. u = up
64. ! Updates the boundary condition on the top.
65. do i = 0,n
66. do j = 0,n
67. u(i,j,n)=usur(time)
68. end do
69. end do
70. r(1:n-1,1:n-1,1:n-1)=ac*up(1:n-1,1:n-1,1:n-1) &
71. -(6.0+ac)*u(1:n-1,1:n-1,1:n-1) &
72. +u(0:n-2,1:n-1,1:n-1)+u(2:n,1:n-1,1:n-1) &
73. +u(1:n-1,0:n-2,1:n-1)+u(1:n-1,2:n,1:n-1) &
74. +u(1:n-1,1:n-1,0:n-2)+u(1:n-1,1:n-1,2:n)
75. error = 1.
76. m = 0
77. rho = 0.0
78. do while ((error
A.0001).and.(m?200))
79. m = m+1
80. oldrho = rho
81. ! Execute SSOR preconditioner
© 2004 by Chapman & Hall/CRC
176 CHAPTER 4. NONLINEAR AND 3D MODELS
82. do l = 1,n-1
83. do j= 1,n-1
84. do i = 1,n-1
85. rhat(i,j,l) = w*(r(i,j,l)+rhat(i-1,j,l)&
86. +rhat(i,j-1,l) +rhat(i,j,l-1))*ra
87. end do
88. end do
89. end do
90. rhat(1:n-1,1:n-1,1:n-1) = ((2.-w)/w)*(6.+ac)
*rhat(1:n-1,1:n-1,1:n-1)
91. do l = n-1,1,-1
92. do j= n-1,1,-1
93. do i = n-1,1,-1
94. rhat(i,j,l) = w*(rhat(i,j,l)+rhat(i+1,j,l) &
95. +rhat(i,j+1,l)+rhat(i,j,l+1))*ra
96. end do
97. end do
98. end do
99. ! Find conjugate direction
100. rho = sum(r(1:n-1,1:n-1,1:n-1)*rhat(1:n-1,1:n-1,1:n-1))
101. if (m.eq.1) then
102. p = rhat
103. else
104. p = rhat + (rho/oldrho)*p
105. endif
106. ! Execute matrix product q = Ap
107. q(1:n-1,1:n-1,1:n-1)=(6.0+ac)*p(1:n-1,1:n-1,1:n-1) &
108. -p(0:n-2,1:n-1,1:n-1)-p(2:n,1:n-1,1:n-1) &
109. -p(1:n-1,0:n-2,1:n-1)-p(1:n-1,2:n,1:n-1) &
110. -p(1:n-1,1:n-1,0:n-2)-p(1:n-1,1:n-1,2:n)
111. ! Find steepest descent
112. alpha = rho/sum(p*q)
113. u = u + alpha*p
114. r = r - alpha*q
115. error = maxval(abs(r(1:n-1,1:n-1,1:n-1)))
116. end do
117. mpcg = m
118. print*, m ,error,u(15,15,15),u(15,15,28)
119. do l = 0,30,3
120. do j = 0,30,3
121. write(6,’(11f12.4)’) (u(i,j,l),i=0,30,3)
122. end do
123. end do
124. end subroutine
© 2004 by Chapman & Hall/CRC
4.5. TIME DEPENDENT 3D DIFFUSION 177
The M
ATLA B code movsolar3d is used to create a time sequence visualiza-
tion of the temperatures inside the slab. In line 1 the M
ATLA B command load
is used to import the table in the file outsolar, which was created by the Fortran
90 code solar3d.m, into a M
ATLAB array also called outsolar. You may need to
adjust the directory in line one to fit your computer. This 2D array will have
48 segments of 121 × 11, that is, outsolar is a 5808 × 11 array. The nested loops
in lines 6-12 store each 121 × 11 segment of outsolar into a 3D 11 × 11 × 11
array A, whose components correspond to the temperatures within the slab.
The visualization is done in line 13 by the M
ATLAB command slice, and this is
can be viewed using the M
AT LAB command mesh as is indicated in line 17.
MATLAB Code movsolar3d.m
1. load c:\MATLAB6p5\work\outsolar;
2. n = 11;
3. mtime = 48;
4. for k = 1:mtime
5. start = (k-1)*n*n;
6. for l = 1:n
7. for j = 1:n
8. for i =1:n
9. A(i,j,l) = outsolar(n*(l-1)+i+start,j);
10. end
11. end
12. end
13. slice(A,n,[10 6],[4])
14. colorbar;
15. section(:,:)=A(:,6,:);
16. pause;
17. % mesh(section);
18. % pause;
19. end
4.5.6 Assessment
The choice of step sizes in time or space variables is of considerable importance.
The question concerning convergence of discrete solution to continuous solution
is nontrivial. If the numerical solution does not vary much as the step sizes
decrease and if the numerical solution seems "consistent" with the application,
then one may be willing to accept the current step size as generating a "good"
numerical model.
4.5.7 Exercises
1. Experiment with dierent step sizes and observe convergence.
© 2004 by Chapman & Hall/CRC
illustrated in Figures 4.5.2 and 4.5.3. Also across section of the temperatures
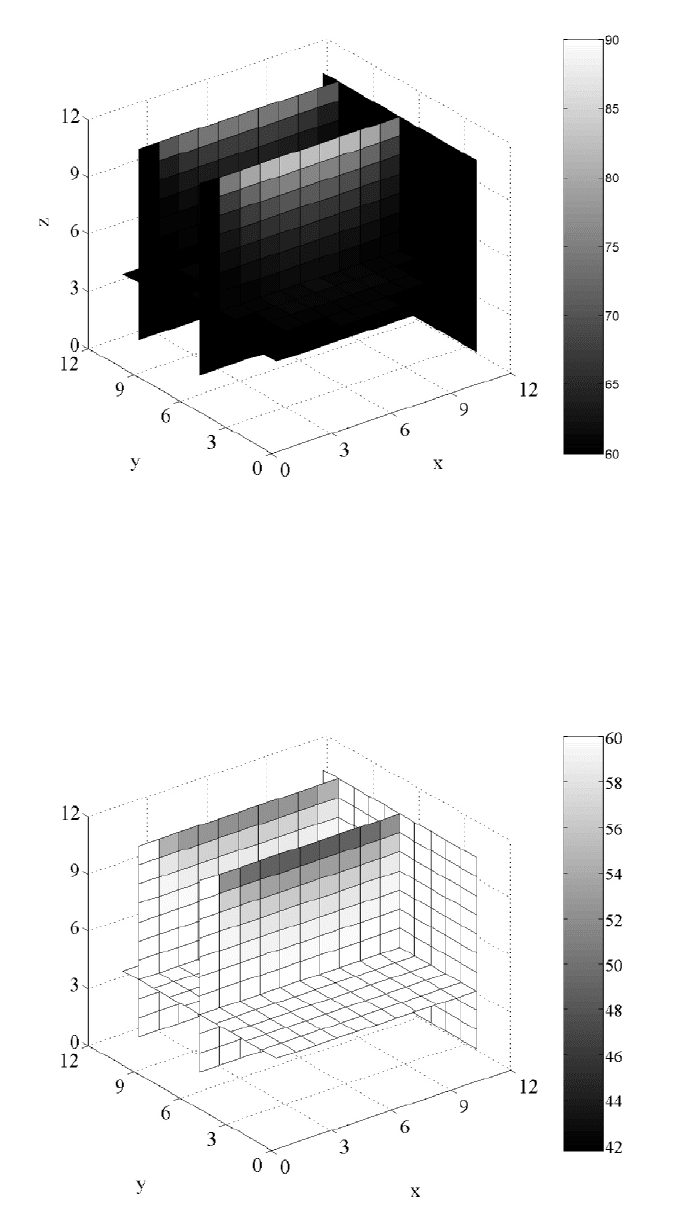
178 CHAPTER 4. NONLINEAR AND 3D MODELS
Figure 4.5.2: Slab is Gaining Heat
Figure 4.5.3: Slab is Cooling
© 2004 by Chapman & Hall/CRC
