Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

2.1. MATCHED ASYMPTOTICS 37

−2 −1.5 −1 −0.5 0 0.5 1 1.5 2

−5

−4

−3

−2

−1

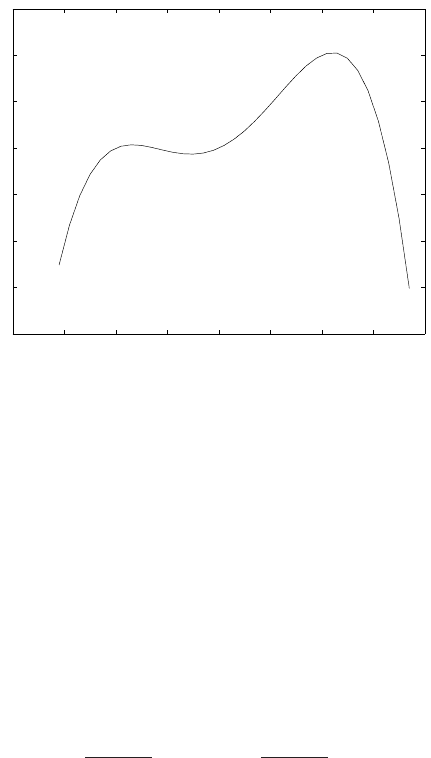
Figure 2.2: Inverted double well potential that illustrates the solution of (2.1.45).

Numerous numerical results conﬁrm that this is indeed the case. Basically, the solution

is very close to u

and u

except in thin layers in which transition b etween u

and u

takes place. To understand the dynamics of u

, we only have to understand the dynamics

of these layers. In particular, our outer solution is simply: U = u

, u

To understand the dynamics of these layers, we assume that they occupy a thin region

around a curve whose conﬁguration at time t is denoted by Γ

. Let ϕ(x, t) = dist(x, Γ

the distance between x and Γ

. We make the ansatz that

∼ U



ϕ(x, t)



+ εU



ϕ(x, t)

, x, t



+ ··· (2.1.43)

Substituting this ansatz into (2.1.42) and balancing the leading order terms in powers of

ε, we get

∂

ϕU

′

(y) = U

′′

(y) − V

′

(y)) (2.1.44)

with the boundary condition: lim

y→±∞

U(y) = u

, u

. This is a nonlinear eigenvalue

problem, with λ = ∂

ϕ as the eigenvalue. Let us write (2.1.44) as

λU

′

(y) = U

′′

(y) − V

′

(y)) (2.1.45)

If we neglect the term on the left hand side of (2.1.44), we obtain Newton’s equation for

an inertial particle in the inverted potential −V (see Figure 2.1.4). Assume that u

< u

Imagine that a particle comes down from u

at y = −∞. Without friction it will pass

38 CHAPTER 2. ANALYTICAL METHODS

through u

at some point and go further down. This is prevented by the the presence

of the term λU

′

which is a friction term. The value of λ gives the just right amount of

friction so that the particle reaches u

as y → +∞.

Multiplying (2.1.44) by U

′

on both sides and integrating, we obtain

∂

∞

−∞

′

(y))

dy = V (u

) − V (u

) (2.1.46)

Since ∂

ϕ = ∂

ϕ/|∇ϕ| = v

, the normal velocity of Γ

, we obtain:

V (u

) − V (u

)

∞

−∞

′

(y))

(2.1.47)

At this time scale (which is sometimes called the convective time scale, in contrast to

the diﬀusive time scale discussed below), the interface moves to the region of lower free

energy, with a constant normal velocity that depends on the diﬀerence in the free energy

of the two phases u

and u

Next we consider the case when V (u

) = V (u

). To be speciﬁc, we will take V (u) =

(1 − u

)

. In this case, at the convective time scale, we have v

= 0, i.e. the interface

does not move. In order to see interesting dynamics for the interface, we should consider

longer time scale, namely, the diﬀusive time scale, i.e. we rescale the problem by replacing

t by tε and obtain

∂

= ∆u

(1 − (u

)

) (2.1.48)

We make the same ansatz as in (2.1.43). The leading order and the next order equations

(in powers of ε) now become

′′

(y) + (1 − U

= 0 (2.1.49)

∂

ϕU

′

= U

′′

|∇ϕ|

+ U

′

∆ϕ + U

(1 − 3U

) (2.1.50)

The solution to (2.1.49) with the boundary condition lim

ϕ→±∞

U(y) = ±1 is given by

U(y) = tanh



√



(2.1.51)

Since |∇ϕ| = 1, (2.1.50) gives

∂

ϕU

′

= U

′′

+ U

′

∆ϕ + U

(1 − 3U

) (2.1.52)

2.2. THE WKB METHOD 39

Multiplying both sides by U

′

and integrating in y, we obtain (note that

∞

−∞

′

′′

(1 − 3U

)}dy = 0)

∂

ϕ = ∆ϕ (2.1.53)

This can also be written as

∂

|∇ϕ|

= ∇ ·

∇ϕ

|∇ϕ|

(2.1.54)

In terms of Γ

, this is the same as

= κ (2.1.55)

where κ is the mean curvature of Γ

Examples of this type are discussed in [?].

2.2 The WKB method

To motivate the WKB metho d , let us look at the ODE

− u

= 0, (2.2.1)

with boundary condition u

(0) = 0 and u

(1) = 1. It is straightforward to ﬁnd the exact

solution to this problem:

= Ae

x/ε

+ Be

−x/ε

, (2.2.2)

where A and B are constants determined by the boundary conditions: A = e

1/ε

/(e

2/ε

−1)

and B = −e

1/ε

/(e

2/ε

−1). One thing we learn from this explicit solution is that it contains

factors with 1/ε in the exponent. Power series expansion in ε will not be able to capture

these terms.

Now consider the problem

− V (x)u

= 0 (2.2.3)

We assume that V (x) > 0 (the case where V changes sign, known as the turning point

problem, is more diﬃcult to deal with, see [?]). This equation can no longer be solved

explicitly. However, motivated by the form of the explicit solution to (2.2.1) , we will look

for approximate solutions of the form

(x) ∼ e

(x)+εS

(x)+O(ε

))

(2.2.4)

40 CHAPTER 2. ANALYTICAL METHODS

Since

∼ (

′′

+ S

′′

+ (

′

+ S

′

)

+ O(1) (2.2.5)

we have

(εS

′′

+ ε

′′

) + (S

′

+ εS

′

)

− V (x) = O(ε

). (2.2.6)

The solution to the leading order equation

′

(x))

− V (x) = 0 (2.2.7)

is given by

= ±

V (y) dy. (2.2.8)

The next order equation

′′

+ 2S

′

= 0 (2.2.9)

gives

= −

log |S

′

| = −

log(V ). (2.2.10)

Therefore, to O(ε), the solution must be a linear combination of the two obtained above

u(x) ∼ A

V (x)

−1/4

√

V (y) dy

+ A

V (x)

−1/4

−

√

V (y) dy

. (2.2.11)

where A

and A

are constants depending on the boundary condition and the starting

point of the integral in the exponent of (2.2.11).

As another example, consider the Schr¨odinger equation

iε∂

= −

∆u

+ V (x)u

, (2.2.12)

with initial condition:

(x, 0) = A(x)e

iS(x)/ε

. (2.2.13)

We will look for approximate solutions in the form:

(x, t) ∼ A

(x, t)e

iS(x,t)/ε

, (2.2.14)

where A

(x, t) ∼ A

(x, t) + εA

(x, t) + ···. Substituting into (2.2.12), we obtain the

leading and next order equations

∂

S +

|∇S|

+ V (x) = 0, (2.2.15)

∂

+ ∇S ·∇A

∆S = 0. (2.2.16)

2.3. AVERAGING METHODS 41

The ﬁrst question above is the Eikonal equation, which happen to be the usual Hamilton-

Jacobi equation in classical mechanics:

∂

S + H(x, ∇S) = 0, (2.2.17)

where H(x, p) = |p|

/2+V (x). The second equation is a transport equation for the lead-

ing order behavior of the amplitude function A

. This establishes a connection between

quantum and classical mechanics via the semi-classical limit ε → 0.

This asymptotic analysis is valid as long as the solution to the Eikonal equation

remains smooth. However, singularities may form in the solutions of th e Eikonal equation,

as is the case of caust ics, and the asymptotic analysis has to be modiﬁed to deal with

such a situation [?].

2.3 Averaging methods

In many problems, the variables t hat describe the state of the system can be split

into a set of slow variables and a set of fast variables, and we are more interested in the

behavior of the slow variables. In situations like this, one can often obtain an eﬀective

model for the slow variables by properly averaging the original model over the statistics

of the fast variables. We discuss such averaging met hods in this section.

2.3.1 Oscillatory problems

Consider the following example:

= −

+ x

(2.3.1)

+ y

(2.3.2)

From now on, for simplicity, we will sometimes neglect the superscript ε. If we replace

(x, y) by the polar coordinates (r, ϕ), we get

dϕ

(2.3.3)

= r (2.3.4)

42 CHAPTER 2. ANALYTICAL METHODS

When ε ≪ 1, the dynamics of the angle variable ϕ is much faster than that of the variable

In general, we may use the action-angle variables and consider systems of the form:

dϕ

ω(I) + f(ϕ, I) (2.3.5)

= g(ϕ, I) (2.3.6)

Here f and g are assumed to be periodic with respect to the angle variable ϕ with period

[−π, π]. We also assume that ω does not vanish. In this example ϕ is the fast variable

and I is the slow variable. Our objective is to derive simpliﬁed eﬀective equations for the

slow variable. For this purpose, we will make use of the multiscale expansion, which is a

very powerful technique that will be discussed in more detail in the next section.

We will look for approximate solutions of (2.3.1) and (2.3.2) in the form:

ϕ(t) ∼ ϕ





+ εϕ



, t



(2.3.7)

I(t) ∼ I

(t) + εI



, t



(2.3.8)

This says that ϕ and I are in principle functions with two scales, but to leading order I

is a function of only the slow scale. Let τ = t/ε. To guarantee that the terms ϕ

and I

in the above ansatz are indeed the leading order terms, we will assume that ϕ

(τ, t) and

(τ, t) grow sublinearly in τ:

(τ, t)

→ 0,

(τ, t)

→ 0 (2.3.9)

as τ → ∞. Substituting the ansatz into (2.3.5), we obtain the following leading order

equations:



dϕ

dτ





− ω(I

(t))



+ O(1) = 0 (2.3.10)

(t) +

∂I

∂τ



, t



− g





, I

(t)



+ O(ε) = 0 (2.3.11)

Our objective is to ﬁnd ϕ

, I

, ϕ

, I

, ··· su ch that the equations above are satisﬁed to as

2.3. AVERAGING METHODS 43

high an order in ε as possible. The leading order equations are:

dϕ

dτ





= ω(I

(t)) (2.3.12)

(t) +

∂I

∂τ



, t



= g





, I

(t)



(2.3.13)

To guarantee that these equations hold, we require:

dϕ

dτ

(τ) = ω(I

(t)) (2.3.14)

(t) +

∂I

∂τ

(τ, t) = g(ϕ

(τ), I

(t)) (2.3.15)

for all values of t and τ , even though the original problem only requires them to hold

when τ = t/ε.

The solution to the ﬁrst equation is given by:

(τ) = ω(I

)τ + ˆϕ

(2.3.16)

Averaging the second equation in τ over a large interval [0, τ], and letting τ → ∞, we

obtain, using the sublinear growth condition:

= lim

τ→∞

g(ϕ

(τ

′

), I

)dτ

′

2π

[−π,π]

g(θ, I

)dθ (2.3.17)

This gives rise to the averaged system:

= G(J), G(J) =

2π

[−π,π]

g(θ, J)dθ (2.3.18)

It is a simple matter to show that for any ﬁxed time T , there exists a constant C such

that

|I(t) − J(t)| ≤ Cε

for 0 ≤ t ≤ T [?]. Therefore in this case, the dynamics of the slow variable is described

accurately by the averaged system.

The story becomes much more complicated when there are more than one degree of

freedom. Consider

dϕ

ω(I) + f(ϕ, I) (2.3.19)

= g(ϕ, I) (2.3.20)

44 CHAPTER 2. ANALYTICAL METHODS

where ϕ = (ϕ

, ··· , ϕ

), I = (I

, ··· , I

), f = (f

, ··· , f

) and g = (g

, ··· , g

). f and

g are periodic functions of ϕ with period [−π, π]

. Formally, the “averaging theorem”

states that for small values of ε, the behavior of the action variable is approximately

described by the averaged system:

= G(J), (2.3.21)

where

G(J) =

(2π)

[−π,π]

g(θ, J)dθ

···dθ

, θ = (θ

, ··· , θ

) (2.3.22)

We put “averaging theorem” in quotation marks since this statement is not always valid

due to the occurence of resonance.

To see how (2.3.21) may arise, we again proceed to look for multiscale solutions of

the type (2.3.7) and (2.3.8), this leads us to

= lim

τ→∞

g(ϕ

(τ

′

), I

)dτ

′

, ϕ

(τ) = ω(I

)τ + ˆϕ

(2.3.23)

Now, to evaluate the right hand side, we must distinguish two diﬀerent cases:

1. When the components of ω(I

) are rationally dependent, i.e. the exists a vector q

with rational components, such that q · ω(I

) = 0. This is the resonant case.

2. When the components of ω(I

) are rationally independent. In this case, the ﬂow

deﬁned by (2.3.16) is ergodic on [−π, π]

(periodically extended).

In the second case, we obtain that

lim

τ→∞

g(ϕ

(τ

′

), I

)dτ

′

(2π)

[−π,π]

g(ϕ, I

)dϕ

···dϕ

(2.3.24)

This gives us the averaged equation (2.3.21)-(2.3.22).

The averaged equation (2.3.21) neglects the resonant case. The r ationale for doing so

is that there are many more rationally independent vectors than the rationally dependent

ones. Therefore, generically, the system will pass through resonances instead of being

locked in resonances. However, it is easy to see that if the system is indeed locked in a

resonance, then the “averaging theorem” may fail.

2.3. AVERAGING METHODS 45

As an example, consider the case when d = 2, ω(I) = (I

, I

), f

= f

= 0, g

0, g

= cos(ϕ

− ϕ

) (see [?]). In this case, G

= G

= 0. Let the initial data be given

by:

(0) = I

(0) = 1, ϕ

(0) = ϕ

(0) = 0

For the original system, we have

(t) = 1, I

(t) = 1 + t.

However the solution of the averaged system with the same initial data is given by:

(t) = J

(t) = 1.

The deviation of I from J comes from the fact that for the original system (2.3.19),

(ϕ

(t), ϕ

(t)) stays on the diagonal in the (ϕ

, ϕ

) plane whereas the averaged system

assumes that (ϕ

(t), ϕ

(t)) is ergodic on the periodic cell [−π, π]

in the ϕ plane.

It should b e noted that the violation of the “averaging theorem” does not mean that

there is a ﬂaw in the perturbation analysis. Indeed, it was clear from the perturbation

analysis that there would be a problem when resonance occurs.

A thorough discussion of this topic can be found in the classic book of Arnold [?].

2.3.2 Stochastic ordinary diﬀerential equations

First, a remark about notation. We will not follow standard practice in stochastic

analysis and uses X

to denote the value of the stochastic process X at time t and ex-

presses stochastic ODEs in terms of stochastic diﬀerentials. Instead, we will use standard

notations for functions and derivatives.

Consider

= f(X, Y, t), X(0) = x (2.3.25)

= −

(Y − X) +

√

W , Y (0) = y. (2.3.26)

Here X is the slow variable and Y is the fast variable,

W is the standard Gaussian white

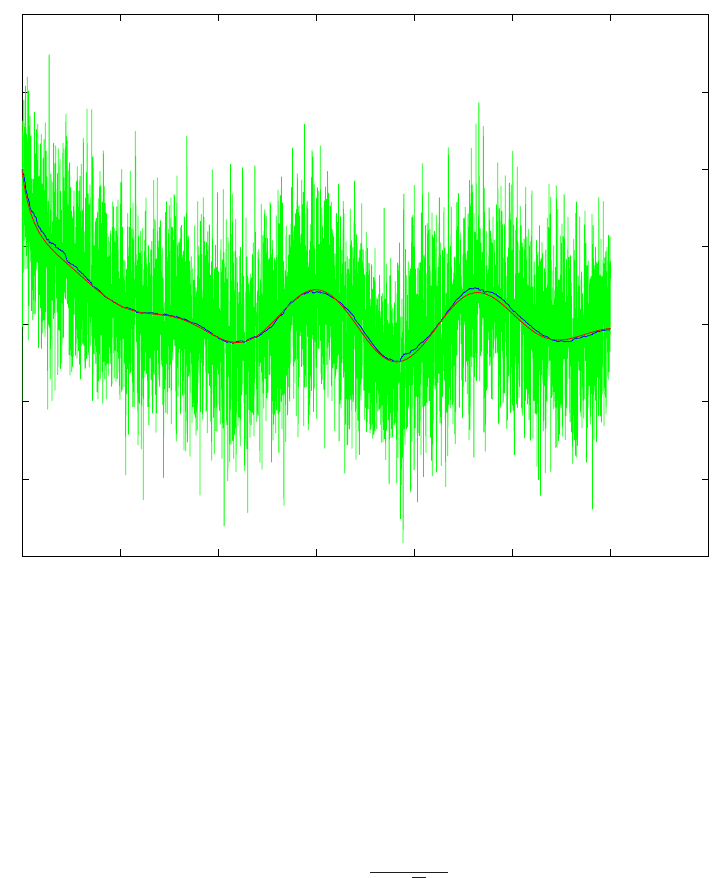
noise. An example of the solution to this problem is shown in Figure 2.3 for the case

when f(x, y, t) = −y

+ sin(πt) + cos(

√

2πt).

46 CHAPTER 2. ANALYTICAL METHODS

0 1 2 3 4 5 6 7

−3

−2

−1

Figure 2.3: The solution of (2.3.25) with x = 2, y = 1, ε = 10

, X(·) and Y (·) are shown

in blue and green respectively. Also shown in red is the solution of the limiting equation

(2.3.29) (courtesy of Eric Vanden-Eijnden).

The equation for Y at ﬁxed X(t) = x deﬁnes an Ornstein-Uhlenbeck process whose

equilibrium density is

∗

(y; x) =

−(y−x)

√

. (2.3.27)

Intuitively, it is quite clear that when ε is small, the X variable in the second equation

does not change very much before Y reaches local equilibrium (set by the local value of

X) in a time scale of O(ε). This means that the dynamics of the fast variable Y is slaved

to that of the slow variable X. Its behavior can be found approximately by holding

the slow variable X ﬁxed (at its instantaneous value) and compute the (conditional)

equilibrium distribution for Y . In addition, the eﬀective dynamics for the slow variable

is obtained by averaging the right hand side of (2.3.25) with respect to the conditional