Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

1.2. MULTI-PHYSICS PROBLEMS 7

to 15 nanometers [41].

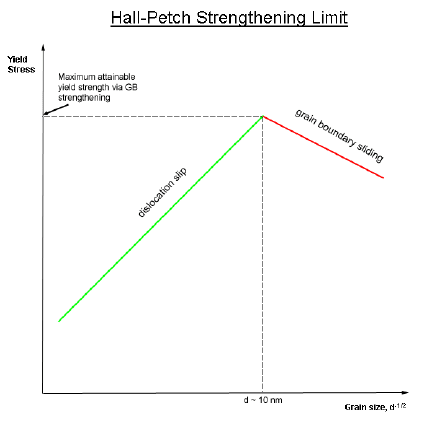
Figure 1.4: An illustration of the Hall-Petch and reverse Hall-Petch eﬀects (from Wikipedia)

All three examples discussed above exhibit a change of behavior as the scales involved

change. The change of behavior is the result of the change of the dominating physical

eﬀects in the system.

1.2.2 Deﬁciencies of the traditional approaches to modeling

Central to any kind of coarse-grained models is the constitutive relation which rep-

resents the eﬀect of the microscopic processes at the macroscopic level. In engineering

applications, the constitutive relations are often modeled empirically based on very simple

considerations such as:

1. second law of thermodynamics;

2. symmetry and invariance properties;

3. linearization or Taylor expansion.

8 CHAPTER 1. INTRODUCTION

These empirical models have been very successful in applications. However, in many

cases, they are inadequate, due either to the complexity of the system or the fact that

they lack crucial information about how the microstructure inﬂuences the macroscale

behavior of the system.

Take the incompressible ﬂuid ﬂow as an example. Conservation of mass and momen-

tum gives

(∂

u + (u · ∇)u) = ∇ · τ, (1.2.3)

∇ · u = 0. (1.2.4)

Here in order to write down the momentum conservation equation, we have to introduce

τ, the stress tensor. This is an object introduced at the continuum level to represent the

short range interaction between the molecules. Imagine a small piece of surface inside

the continuous medium, the stress τ represents the force due to the interaction between

the molecules on both sides of the surface. Ideally the value of τ should be obtained

from the information about the dynamics of the molecules that make up the ﬂuid. This

would be a rather diﬃcult task. Therefore in practice, τ is often modeled empirically,

through intelligent guesses and calibration with experimental data. For simple isotropic

ﬂuids, say made up of spherical particles, isotropy and Galilaean invariance implies that

τ should not depend on u. Hence the simplest guess is that τ is a function of ∇u. In

the absence of further information on the b ehavior of the system, it is natural to start

with the simplest choice, namely that τ is a linear function of ∇u. In any case, every

function is approximately linear in appropriate regimes. Using isotropy, we arrive at the

constitutive relation for Newtonian ﬂuids:

τ = −pI + µ(∇u + (∇u)

) (1.2.5)

where p is the pressure. Substitu ting this constitutive relation into the conservation laws

leads to the well-known Navier-Stokes equation.

It is remarkable that such simple-minded consideration yields a model, the Navier-

Stokes equation, which has proven to be very accurate in describing the dynamics of

simple ﬂuids under a very wide range of conditions. Partly for this reason, a lot of eﬀort

has gone into extending such an approach to modeling complex ﬂuids such as polymeric

ﬂuids. However, the result there is rather mixed [12]. The accuracy of such constitutive

laws is often questionable. In many cases, the constitutive relations become quite compli-

cated. Too many parameters need to be ﬁtted, the physical meaning of these parameters

1.2. MULTI-PHYSICS PROBLEMS 9

becomes obscure. Consequently the original appeal of simplicity and universality is lost.

In addition, there are no systematic ways of developing such empirical constitutive re-

lations. A constitutive relation obtained by calibrating against one set of experimental

data may not be useful in a diﬀerent experimental setting. More importantly, such an ap-

proach does not contain any explicit information about the interaction between ﬂuid ﬂow

and the conformation of the molecules, which might be exactly the kind of information

that we are most interested in.

The situation described above is rather generic. Indeed empirical modeling of consti-

tutive relations is a very popular tool used in many areas, including:

1. Constitutive relations in elasticity and plasticity theory of solids

2. Empirical potentials in molecular dynamics

3. Empirical models of reaction kinetics

4. Hopping rates in kinetic Monte Carlo models

5. Collision cross section for the kinetic theory of gases

These constitutive relations are typically quite adequate for simple systems, such as small

deformation of solids, but fails for complex systems. When empirical models become

inadequate, we have to replace them by more accurate models that rely more on a

detailed description of the microscopic processes.

The other extreme is the quantum many-body theory which is the true ﬁrst principle.

Assume that our system of interest has M nuclei and N electrons. At the level of quantum

mechanics, this system is described by a wavefunction of the form (neglecting spins):

Ψ = Ψ (R

, R

, ··· , R

, r

, ··· , r

)

The Hamiltonian for this system is given by:

H = −

J=1

∇

−

k=1

∇

J<K

− R

−

J,k

− r

i<j

− r

(1.2.6)

where Z

is the nuclear charge of the J-th nucleus. Here all we need in order to analyze a

given system is to input the atomic numbers for the atoms in the system and then solve the

10 CHAPTER 1. INTRODUCTION

Schr¨odinger equation. There are no empirical parameters to ﬁt! The diﬃculty, however,

lies in the complexity of its mathematics. This situation is very well summarized by the

following remark of Paul Dirac, made shortly after the discovery of quantum mechanics

[22]:

“The underlying physical laws necessary for the mathematical theory of a large part

of physics and the whole of chemistry are thus completely known, and the diﬃculty is

only that the exact application of these laws leads to equations much too complicated to

be soluble.”

The mathematical complexity noted by Dirac is indeed quite daunting: The wave-

functions have as many (or, three times as many) independent variables as the number

of electrons and nuclei in the system. If the system has 10

electrons, then the wave-

function has 3 × 10

independent variables. Obtaining accurate information for such

a function is quite an impossible task. In add ition, such a ﬁrst principle model often

gives far too much information, most of which is not really of any interest. Getting the

relevant information from this vast amount of data can also be quite a challenge.

This dicotomy is the kind of situation that we encounter for many problems: Empiri-

cally obtained macroscale models are very eﬃcient but are often not accurate enough, or

lack crucial microstructural information that we are interested in. Microscopic models,

on the other hand, may oﬀer better accuracy, but they are often too expensive to be

used t o model systems of real interest. It would b e nice to have a strategy that combines

the eﬃciency of macroscale models and the accuracy of microscale models. This is a tall

order, but is precisely the motivation for multiscale modeling.

1.2.3 The multi-physics modeling hierarchy

Between the macroscale models and the quantum many-body problem lie a hierarchy

of other models, which are better suited at the appropriate scales. This is illustrated in

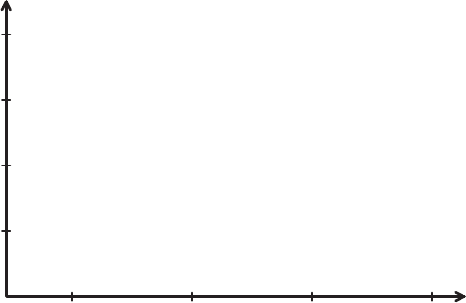
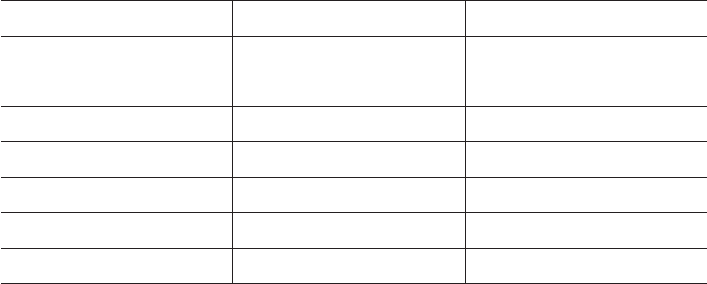
Figure 1.5. A more detailed description of this modeling hierarchy is shown in Table 1.5.

In traditional approaches to modeling, we tend to focus on one particular scale, the

eﬀects of smaller scales are modeled through the constitutive relation, eﬀects of larger

scales are neglected by assuming that the system is homogeneous at larger scales. The

philosophy of multiscale, multi-physics mo d eling is the opposite. It is based on the

1.2. MULTI-PHYSICS PROBLEMS 11

1fs

1ps

1µs

1µm 1m1nm1A˚

time

space

Quantum

Mechanics



Molecular

Dynamics

Kinetic

Theory

Continuum

Mechanics

Figure 1.5: Commonly used models of physics at diﬀerent scales

viewpoint that:

1. Any system of interest can always be described by a hierarchy of models of dif-

ferent complexity. This allows us to think about more detailed models when a

coarse-grained model is no longer adequate. It also gives us a basis for understand-

ing coarse-grained m odels from more detailed ones. In particular, when empiri-

cal coarse-grained models are inadequate, one might still be able to capture the

macroscale behavior of the system with the help of the microscale models.

2. In many situations, the system of interest can be described adequately by a coarse-

grained model, except in some small regions where more detailed models are needed.

These small regions may contain singularities, defects, chemical reactions, or some

other interesting events. In such cases, by coupling models of diﬀerent complexity in

diﬀerent regions, we may b e able develop modeling strategies that have an eﬃciency

that is comparable to the coarse-grained models, as well as an accuracy that is

comparable to that of the more detailed models.

Such strategies have already been explored for quite some time. Two classical exam-

ples are the QM-MM (quantum mechanics-molecular mechanics) modeling of chemical

reactions involving macromolecules, initiated in the 1970’s by Warshel and Levitt [48],

12 CHAPTER 1. INTRODUCTION

Gases, plasmas Liquids Solids

Gas dynamics Hydrodynamics Elasticity models

MHD (Navier-Stokes) Plasticity models

Dislocation dynamics

Kinetic theory Kinetic theory

Brownian dynamics Kinetic Monte Carlo

Particle models Molecular dynamics Molecular dynamics

Quantum mechanics Quantum mechanics Quantum mechanics

Table 1.1: The multi-physics hierarchy

and the ﬁrst-principle-based molecular dynamics, initiated in the 1980’s by Car and Par-

rinello [16]. Both methods have been very successful and have become standard tools in

computational science. However, what triggered the wide-spread of interest on multiscale

modeling in recent years is the realization that such strategies are useful not just for a

few isolated problems, but for a very wide spectru m of problems in all areas of science

and engineering. This is indeed a conceptual breakthrough, and a much more mature

viewpoint on modeling.

To make this really useful, we need to understand the relation between the diﬀerent

models and how to formulate coupled models. Much of the present volume is devoted to

these issues.

1.3 Analytical methods

We will begin with a discussion of the most important analytical techniques for mul-

tiscale problems. We will fo cus on asymptotic analysis tools since they tend to be most

eﬀective. It should be emphasized that these asymptotic techniques are not blank checks.

To use them eﬀectively, one often has to have some intuition about how the solutions be-

have. The asymptotic techniques can then be used as a systematic procedu re for reﬁ ning

that intuition and giving quantitatively accurate predictions.

Matched asymptotics

This is useful for problems whose solutions undergo rapid variations in localized re-

1.4. NUMERICAL METHODS 13

gions. These localized regions are called inner regions. Typical examples are problems

with boundary layers or internal layers. Matched asymptotics is a systematic way of

ﬁnding approximate solutions to such problems, by introducing stret ched variables in

the inner region and matching the approximate solutions in the inner and outer regions.

As a result, we often ﬁnd that the proﬁle of the solution in the inner region is rather

rigid and is parametrized by a few parameters or functions which can be obtained from

the solutions in the outer region.

Averaging and homogenization methods

This is a systematic procedure based on the multiscale expansion [9, 32]. In the case

of ODEs, the objective is to ﬁnd eﬀective dynamical equations for the slow variables by

averaging out the fast variables. There is a natural extension of such techniques to PDEs,

for example, discussed in [10].

Scaling and renormalization group methods

Another important technique is scaling. In its simplest form, it is dimensional analy-

sis. A more systematic approach is the renormalization group analysis, which has become

a very powerful tool in analyzing complex systems.

1.4 Numerical methods

1.4.1 Linear scaling algorithms

We will distinguish two diﬀerent classes of multiscale algorithms. The ﬁrst class are

algorithms that aim at resolving eﬃciently the details of the solutions, including the de-

tailed small scale behavior. Multigrid method (MG), the fast multipole method (FMM),

and adaptive mesh reﬁnement (AMR) are examples of this type. They all make heavy use

of the multiscale structure of the problem. We call these classical multiscale algorithms.

These are typically linear scaling algorithms, in the sense that their computational com-

plexity scales linearly with the numb er of degrees of freedom necessary to represent the

detailed microscale solution. We are also going to include the domain decomposition

method (DDM). Even though it relies less on the multiscale structure of the problem,

it does provide a platform on which multiscale methods can be constructed, particularly

for the kind of problems discussed in Chapter 7 for which the solutions behave very

14 CHAPTER 1. INTRODUCTION

diﬀerently on diﬀerent domains.

1.4.2 Sublinear scaling algorithms

Recent eﬀorts on multiscale modeling have focused on sublinear scaling algorithms.

These are algorithms whose computational complexity scales sublinearly with the number

of degrees of freedom necessary to represent the detailed microscale solution:

Computational complexity

Number of degrees of freedom for the microscale model

≪ 1

This may seem to o good to be true. Indeed it is only possible to construct such algorithms

1. if our aim is to resolve certain features of the microscale solution such as some

averaged quantities, not its detailed behavior; and

2. if the microscale model has some particular features that we can take advantage of.

A typical example of such particular features is scale separation.

Even though multiscale problems are typically quite complicated, one main objective of

multiscale modeling is to identify special classes of such problems for which it is possible

to develop simpliﬁed descriptions or algorithms. The eﬃciency of these algorithms relies

on these special features of the problem. Therefore they are less general than the linear

scaling algorithms discussed earlier. A good example for illustrating this diﬀerence is the

Fourier transform. The well-known fast Fourier transform (FFT) is almost linear scaling

and is completely general. However, if t he Fourier coeﬃcients are sparse, then one can

develop sublinear scaling algorithms, as was done in [28]. Of course it is understood

that the improved eﬃciency of such sublinear scaling algorithms can only be expected

for special situations, i.e. when the Fourier coeﬃcients are sparse.

In practice there may not be a sharp division between linear and sublinear scaling

algorithms.

1.4.3 Type A and type B multiscale problems

It is helpful to distinguish two classes of multiscale problems. The ﬁrst are problems

with local defects or singularities, such as dislocations, shocks and boundary layers, for

which a macroscale mo del is suﬃcient for most of the physical domain and the microscale

1.4. NUMERICAL METHODS 15

model is only needed locally around the singularities or heterogeneities. The second class

of problems are those for which the microscale model is needed everywhere either as a

supplement to or as the replacement of the macroscale model. This occurs, for example,

when the microscale model is needed to supply the missing constutitive relation in the

macroscale model. We will call the former type A problems and the latter type B problems

[24]. The central issues and the main diﬃculties can be quite diﬀerent for the two classes

of problems. The standard approach for type A problems is to use the microscale model

near defects or heterogeneities and the macroscale model elsewhere. The main question

is how to couple these models at the interface where the two models meet. The standard

approach for type B problems is to couple the macro and micro models everywhere in

the computational domain, as is done in the heterogeneous multiscale method (HMM)

[24]. Note that for type A problems, the macro-micro coupling is lo calized. For type B

problems, coupling is done over the whole computational domain.

1.4.4 Concurrent vs. sequential coupling

Historically, multiscale (multi-physics) modeling was ﬁrst used in the form of sequen-

tial (or serial) coupling: The macroscopic model was determin ed ﬁrst, except for some

parameters, or functions, which are then computed or tabulated using a microscopic

model. Function values that are not found in the table can b e obtained using interpola-

tion. At the end of this procedure, one has a macroscopic model which can then be used

to analyze the macroscopic behavior of the system under diﬀerent conditions. For obvious

reasons, this coupling procedure is also called precomputing, or microscopically-informed

modeling. A typical example is found in gas dynamics, where one often precomputes the

equation of state using kinetic theory and stores it as a look-up table. This information

is then used in Euler’s equations of gas dynamics to simulate gas ﬂow under diﬀerent

conditions. When modeling porous medium ﬂows, a common form of upscaling is t o pre-

compute the eﬀective permeability tensor K(x) using the representative averaging volume

(RAV) technique [8]: One considers a domain of suitable size (i.e. the representative av-

eraging volume) around x, and solves the microscale model in that domain. The result

is then suitably averaged to give K(x) [23]. Finally, this eﬀective permeability tensor is

used in Darcy’s law

v(x) = −K(x)∇p(x), ∇ · v(x) = 0

16 CHAPTER 1. INTRODUCTION

to compute the pressure ﬁeld on larger scale. More recently, such a sequential multiscale

modeling strategy has been used to study macroscopic propert ies of ﬂuids and solids usin g

parameters that are obtained successively starting from models of quantum mechanics

[19, 46].

If the missing information is a function of many variables, then precomputing such

a function might be too costly. For this reason, sequential coupling has been limited

mainly to situations when the needed information is just a small number of parameter

values or functions of very few variables. Indeed, for this reason, sequential coupling is

often referred to as parameter passing.

An alternative approach is to obtain the missing information “on the ﬂy” as the

computation proceeds. This is commonly referred to as the concurrent coupling approach

[1]. It is preferred when the missing information is a function of many variables. Assume

that we are solving a macroscopic model in d dimension, with mesh size ∆x, and we

need to obtain some data from a microscopic model at each grid point. The number of

data evaluation in a concurrent approach would be roughly O((∆x)

−d

). In a sequential

approach, assuming that the needed data is a function of m variables, then the number

of force evaluation in the precomputing stage would be O(h

−m

) if a uniform grid of size

h is used in the computation. Assuming that h ∼ ∆x, then the concurrent approach is

more eﬃcient if m > d. This is certainly the case in Car-Parrinello molecular dynamics

(see Chapter 6) where the inter-atomic forces are functions of all atomic coordinates.

Hence m can easily be on the order of thousands.

However, as was pointed out in [27], the eﬃciency of precomputing can be im-

proved with more eﬃcient look-up tables and interpolation techniques. For example,

if sparse grids are used and if the grid size is h, then the number of grid points needed

is O(|log(h)|

m−1

/h). This is signiﬁcantly less than the cost on the uniform grid, making

precomputing quite feasible if m is below 8 or 10. Examples of the application of sparse

grids to sequential coupling can be found in [27].

The most appropriate approach for a particular problem depends a lot on how much

we know about the macroscale process. Take again the example of incompressible ﬂuids.

We know that the macroscale model should be in the form of (1.2.3). The only issue is

the form or expression of τ. We can distinguish three cases.

1. A linear constitutive relation is suﬃciently accurate. We only need to know the

value of the viscosity coeﬃcient µ in (1.2.5).