Wegener I. Complexity Theory. Exploring the Limits of Efficient Algorithms

Подождите немного. Документ загружается.

Additional Complexity Classes and

Relationships Between Complexity Classes

10.1 Fundamental Considerations

In Chapter 3 we introduced and investigated the fundamental complexity

classes. The relationships between them were summarized in Theorem 3.5.3.

Reductions serve to establish relationships between individual problems. If a

problem is compared with a complexity class C,itcanprovetobeC-easy, C-

hard, C-complete, or C-equivalent. In this way we learn something about the

complexity of problems in relation to the complexity of other problems and

in relation to complexity classes. The theory of

NP-completeness has proven

itself to be the best tool currently known for classifying as diﬃcult many

important problems under the hypothesis that

NP = P.

And so we have convinced ourselves that the investigation of complexity

classes like

NP that are deﬁned in terms of algorithms that are not practically

eﬃcient can nevertheless be well-motivated.

In this chapter we return to these fundamental complexity classes and de-

ﬁne new classes as well. We begin in Section 10.2 with the inner structure of

NP and co-NP. In Section 10.4 we deﬁne and investigate the polynomial hierar-

chy of complexity classes that contain

NP. To that end we deﬁne oracle classes

in Section 10.3. While a Turing reduction may make use of an algorithm for

a particular problem, we will now allow algorithms for any problem in an en-

tire complexity class. We obtain new complexity theoretical hypotheses, some

of which are stronger than the

NP = P-hypothesis but still well-supported. In

later chapters we will draw consequences from these hypotheses that we do

not (yet) know how to derive from

NP = P. In addition we obtain indications

about which proof methods we cannot use to prove the

NP = P-conjecture.

Of course, all this begs the question, why all these considerations are re-

lated to

NP and classes above NP, and why we don’t continue with an in-

vestigation of algorithmically relevant classes like

ZPP, RP, co-RP,andBPP.

The main reason is that

BPP = P is not as well-supported a hypothesis as

NP = P. While we suspect that the NP-complete problems (and therefore a

great number of well-studied problems) do not belong to

P, there are hardly

128 10 Additional Complexity Classes

any such problems that we know belong to BPP but suspect do not belong

P. A proof that BPP = P would be a far-reaching and strong result, but it

would not bring down the currently reigning view of the world of complexity

classes – in contrast to a proof of

NP = P. Among experts, the opinion is

widely held that “

P is close to BPP” but that P and NP are separated by the

world of

NP-complete problems. The notion “is close to” is, of course, not for-

malizable. We will further support these considerations in Section 10.5 where

we investigate the relationship between

NP and BPP.

10.2 Complexity Classes Within NP and co-NP

If NP = P,thensinceP = co-P it follows that co-NP = P andweonlyhavethe

class of eﬃciently solvable problems. This is not only unexpected, it is also

less interesting than the other case. From Section 5.1 we know that in

P there

are three equivalence classes with respect to the equivalence relation ≡

• all problems for which no input is accepted,

• all problems for which all inputs are accepted, and

• all other problems.

NP = P, then by deﬁnition the class NPC of all NP-complete problems

forms a fourth equivalence class with respect to ≡

. Are there still more

equivalence classes? This is equivalent to the question of whether or not the

class

NPI := NP −(P ∪ NPC) is empty. Of course, we can’t prove that any

problem belongs to

NPI, since then we would have proven that NP = P.But

perhaps there are problems that we suspect belong to

NPI? Garey and Johnson

(1979) list three problems which at that time were considered candidates for

membership in

NPI:

• the problem of linear programming (

LP), i.e., the problem of determining

whether a linear function on a space restricted by linear inequalities takes

on a value at least as large as a given bound b;

• primality testing (

Primes); and

• the graph isomorphism problem (

GraphIsomorphism, or sometimes more

brieﬂy abbreviated as

GI; see also Section 6.5).

It has been known for a long time already that

LP ∈ P (see, for example,

Aspvall and Stone (1980)).

Primes was known to belong to NP, co-NP,and

even

co-RP. Miller (1976) had already designed a polynomial-time primality

test based on an unproven hypothesis from number theory. So

Primes was also

a candidate for membership in

P. Finally, Agrawal, Kayal, and Saxena (2002)

were able to prove that in fact

Primes ∈ P. Their arguments, however, have

no consequences for the complexity of the factoring problem

Fac t . The proof

that a number n is not prime is based on number theoretic arguments that

have not (yet) been any help in computing a divisor of n. The conjecture that

Fac t is not polynomial-time solvable has not been shaken by the discovery of a

10.2 Complexity Classes Within NP and co-NP 129

polynomial-time primality test. In particular, cryptographic protocols like the

RSA system and PGP that are based on the supposed diﬃculty of factoring,

cannot be attacked with this primality test.

For

GI there are no indications that GI ∈ P. In Chapter 11 we will provide

support for the conjecture that

GI is not NP-complete. So for the moment, GI

is the best-known decision problem that is conjectured to belong to NPI.

Since we want to concentrate on results about concrete algorithmic prob-

lems, the following existence result of Ladner (1975) will only be cited.

Theorem 10.2.1. If

NP = P, then NPI is not empty and, in fact, contains

problems that are incomparable with respect to ≤

. 

So if

NP = P, then there are several ≡

-equivalence classes within NPI.

The power of the concept of polynomial reductions can be seen in the

fact that almost all problems of interest have been proven to be either

NP-equivalent or polynomial-time solvable. But if NP = P, then there

is actually a rich structure of problems between

P and NPC.

We want to discuss the relationship between

NP and co-NP. They are duals

of each other since by deﬁnition

co-co-NP = NP. This means that either NP =

co-NP or neither class contains the other, since from NP ⊆ co-NP it follows

that

co-NP ⊆ co-co-NP = NP. In Section 5.3 we characterized NP using a

polynomially bounded existential quantiﬁer and polynomial-time predicates.

Formally, L ∈

NP if and only if there is a language L



∈ P and a polynomial

p such that

L =



x |∃z ∈{0, 1}

p(|x|)

:(x, z) ∈ L





Languages in

co-NP can be characterized in a dual manner. Formally, the exis-

tential quantiﬁer is replaced by a universal quantiﬁer. The

NP = P-hypothesis

means that without the existential quantiﬁer we cannot describe as many lan-

guages as with it. If we believe that in this sort of representation existential

quantiﬁers cannot be replaced with universal quantiﬁers (and other languages



∈ P), then this is equivalent to the NP = co-NP-hypothesis. As was explained

at the beginning of this section, a proof that

NP = co-NP implies that NP = P.

We have also seen that to prove that

NP = co-NP, it suﬃces to show that

NP ⊆ co-NP. The following line of thought is intuitively obvious: If a hardest

problem in

NP,thatisanNP-complete problem, belongs to co-NP,thenallof

NP belongs to co-NP. We will use this kind of reasoning often, so we formalize

it here.

Theorem 10.2.2. If L is

NP-complete and L ∈ co-NP, then NP = co-NP.

Proof. As we have already discussed, it is suﬃcient to show that under the

hypotheses of the theorem, if L



∈ NP,thenL



∈ co-NP. But this is equivalent

L ∈ NP. We describe a polynomial-time bounded nondeterministic Turing

130 10 Additional Complexity Classes

machine that accepts inputs w ∈



and rejects input w/∈ L



.SinceL is NP-

complete and L



∈ NP, L



≤

L. So there is a polynomial-time computable

function f such that

w ∈ L



⇔ f(w) ∈ L.

We apply this function f to the input w for



. It follows that

w ∈



⇔ f(w) ∈ L.

Since L ∈

co-NP, we can nondeterministically check whether f (w) ∈

L in

polynomial time, and so we have a polynomial-time nondeterministic test for

whether w ∈



. 

The

NP = co-NP-hypothesis implies that languages L ∈ NP ∩ co-NP are nei-

ther

NP-complete nor co-NP-complete. Before the proof that Primes ∈ P,the

fact that

Primes ∈ NP ∩ co-NP was the best indication that Primes was nei-

ther

NP-complete nor co-NP-complete. For the graph isomorphism problem we

know that

GI ∈ NP, but we do not know if GI ∈ co-NP.Sothiskindofcon-

sideration provides no support for the conjecture that

GI is not NP-complete.

Finally, the

NP = co-NP-hypothesis implies that NP-complete problems do

not belong to

co-NP. Therefore, it is not surprising that we have not been able

to represent any of the known

NP-complete problems with universal quantiﬁers

and thus show them to belong to

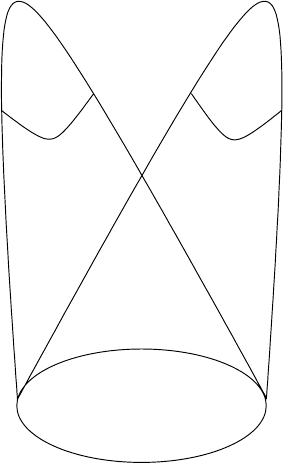
co-NP. In summary, we conjecture that the

world within

NP ∪ co-NP is as illustrated in Figure 10.2.1.

10.3 Oracle Classes

Already when we introduced Turing reductions A ≤

B in Section 4.1 we

spoke of polynomial-time algorithms for A with oracle B. We will continue to

use the notion of an oracle, although this term sounds somewhat mysterious

and imprecise. In fact, we are simply talking about a subprogram for B,a

call to which (usually called a query) is assigned a cost of 1. The term oracle

is perhaps an unfortunate choice, but it is the usual designation for this sort

of subprogram. Since we will only consider oracles for decision problems, we

don’t have to concern ourselves with how one should measure the cost of an

oracle query when the response is longer than the question.

Deﬁnition 10.3.1. The complexity class

P(L) for a decision problem L con-

tains all decision problems L



such that L



≤

L, that is, all problems L



that

can be decided by polynomial-time algorithms with access to an oracle for L.

The complexity class

P(C) for a class C of decision problems is the union of

all

P(L) with L ∈C.

If the complexity class C contains a ≤

-or≤

-complete problem L

∗

,then

P(C)=P(L

∗

), since each query to an oracle L ∈Ccan be replaced by a

polynomial-time algorithm that queries oracle L

∗

.Inparticular,P(NP)=

10.3 Oracle Classes 131

NPI

∩co-NPI

co-NPI

co-NP

NPC

NPI

co-NPC

Fig. 10.2.1. The complexity world within NP ∪ co-NP under the assumption that

NP ∩ co-NP = P.

(Sat). We suspect that P (NP) is a strict superclass of NP. Otherwise we

would be able to replace all the queries to

Sat in a polynomial-time algorithm

with a single query at the very end, the answer to which we would not be

allowed to change. In particular,

co-NP ⊆ P(NP) since we can reverse the

answer of the

NP-oracle. These arguments even suggest that P(NP) is a strict

superclass of

NP ∪ co-NP. We can’t prove any of this, however, since NP = P

would imply that P(NP)=P(P)=P.

This operator cannot be iterated, since

P(P(C)) = P(C): A polynomial-time

computation in which we may make queries to a polynomial-time computation

with oracle L is nothing more than a polynomial-time computation with oracle

In our earlier considerations, it was an important step to consider

NP in

addition to

P. So now we want to consider NP(L)andNP(C) in addition to

P(L)andP(C).

Deﬁnition 10.3.2. For a decision problem L, the complexity class

NP(L) con-

tains all decision problem L



for which there is a nondeterministic polynomial-

time algorithm with oracle L. For a class of decision problems C,thecomplex-

ity class

NP(C) is the union of all NP(L) for L ∈C.

P(P)=P and NP(P)=NP, since the oracle queries can be replaced by

(deterministic) polynomial-time algorithms. In order to become more familiar

132 10 Additional Complexity Classes

with these notions, we introduce a practically important problem that belongs

co-NP(NP) but is conjectured not to belong to either P(NP)orNP(NP). The

language of all minimal circuits over all binary gates (

MC) consists of all

circuits with one output gate for which there is no circuit with fewer gates

that computes the same Boolean function.

Theorem 10.3.3.

MC ∈ co-NP(NP).

Proof. We will show that the complement

MC is in NP(NP). Let C be a

circuit, and let f be the function computed by C. In polynomial time we

nondeterministically generate a circuit C



that has fewer gates than C.The

function computed by C



we denote f



.FromC and C



we form with one

additional gate of type ⊕ (exclusive or) a new circuit C



for which f



= f ⊕f



As oracle we select the

NP-complete satisﬁability problem for circuits, which

we denote

Sat

cir

. The oracle accepts C



if and only if there is some a such

that f



(a) = 1, that is, if and only if there is an a such that f



(a) = f(a). In

this case, the algorithm rejects C. If the oracle rejects C



,thenf



= f ,andC



is a smaller circuit that computes the same function that C computes. So the

algorithm knows that C is not minimal and accepts C.ThusC is accepted on

at least one computation path if and only if C is not minimal, as was desired.



As a ﬁnal note, we point out that there is an alternative “exponential”

notation for these classes that is also common in the literature. In this notation

and NP

are used in place of P(C)andNP(C), for example.

10.4 The Polynomial Hierarchy

In Section 10.3 we prepared the tools to deﬁne a multitude of complexity

classes. We will travel this path formally and look at a few properties of

these complexity classes. Along the way, we will see that these complexity

classes have clear, logical descriptions, from which we can construct complete

problems. Their description supports the hypothesis that these complexity

classes form a genuine hierarchy, that is, they form an increasing sequence of

distinct complexity classes with respect to set inclusion.

Deﬁnition 10.4.1. Let Σ

:= NP, Π

:= co-NP,and∆

:= P.Fork ≥ 1,let

• Σ

k+1

:= NP(Σ

• Π

k+1

:= co-Σ

k+1

,and

• ∆

k+1

:= P(Σ

The polynomial hierarchy (

PH) is the union of all Σ

for k ≥ 1.

It is also consistent to let Σ

= Π

= ∆

= P, and to extend the deﬁnition

to all k ≥ 0. As we saw in Section 10.3, Σ

= NP, Π

= co-NP and ∆

= P.

10.4 The Polynomial Hierarchy 133

With the new notation, the statement if Theorem 10.3.3 can be expressed as

MC ∈ Π

. We list a few properties of the new complexity classes in order to

get a picture of the relationships between them.

Lemma 10.4.2. For the complexity classes within the polynomial hierarchy

we have the following relationships:

• ∆

= co-∆

= P(∆

) ⊆ Σ

∩ Π

⊆ Σ

∪ Π

⊆ ∆

k+1

= P(Π

• Σ

k+1

= NP(Π

)=NP(∆

k+1

• Π

k+1

= co-NP(Π

)=co-NP(∆

k+1

• Σ

⊆ Π

⇒ Σ

= Π

Proof. We have ∆

= co-∆

, since by deﬁnition ∆

= P(Σ

k−1

)andwith

Turing-reductions we can negate the answer at the end. Also,

P(∆

P(P(Σ

k−1

)) = P(Σ

k−1

)=∆

, since a polynomial algorithm that may query

a polynomial-time algorithm with oracle L ∈ Σ

k−1

is nothing more than a

polynomial-time algorithm that may make queries to the oracle L ∈ Σ

k−1

⊆

∆

. Clearly ∆

= P(Σ

k−1

) ⊆ NP(Σ

k−1

)=Σ

,and∆

= co-∆

⊆ Π

The inclusion

P(C) ⊆ NP(C) holds by deﬁnition for all complexity classes

C. Similarly, it follows from the deﬁnitions that Σ

⊆ P(Σ

)=∆

k+1

and

= co-Σ

⊆ co-∆

k+1

= ∆

k+1

. Finally, ∆

k+1

= P(Σ

)=P(Π

), since an

oracle L ∈ Σ

is of the same use as an oracle

L ∈ co-Σ

= Π

.Wecansimply

reverse the answers to the oracle queries.

By the same argument it follows that Σ

k+1

= NP(Σ

)=NP(Π

). From

⊆ ∆

k+1

it follows that Σ

k+1

= NP(Σ

) ⊆ NP(∆

k+1

). For the reverse

direction we must argue that an oracle L ∈ ∆

k+1

can be replaced by an

oracle L



∈ Σ

.Since∆

k+1

= P(Σ

), an oracle L ∈ ∆

k+1

can be replaced

by a polynomial-time algorithm with oracle L



∈ Σ

. The result is a non-

deterministic polynomial-time algorithm that queries a polynomial-time algo-

rithm with oracle L



The third statement follows from the second by taking complements.

Finally, Σ

⊆ Π

, implies that Π

= co-Σ

⊆ co-Π

= Σ

and thus that

= Π

. 

Analogous to the representations in Chapter 3, we obtain the complexity

landscape within the polynomial hierarchy depicted in Figure 10.4.1.

The conjecture that the classes of the polynomial hierarchy form a gen-

uine hierarchy contains the conjecture that all the inclusions in Figure 10.4.1

are strict inclusions and that the classes Σ

and Π

are incomparable with

respect to set inclusion. Thus we obtain the following complexity theoretical

hypotheses:

• Σ

= Σ

k+1

• Π

= Π

k+1

• Σ

= Π

• ∆

= Σ

∩ Π

= Σ

∪ Π

= ∆

k+1

134 10 Additional Complexity Classes

∪ Π

∩ Π

∪ Π

= NP ∪ co-NP

= NP Π

= co-NP

∩ Π

= NP ∩ co-NP

∆

= P

∆

Fig. 10.4.1. The complexity landscape within the polynomial hierarchy. Arrows

represent set inclusion.

Before investigating relationships between these hypotheses, we will derive

a logical representation of the complexity classes Σ

and Π

. This will simplify

later considerations.

Theorem 10.4.3. A decision problem L belongs to the class Σ

if and only

if there is a polynomial p and a decision problem L



∈ P such that for A =

{0, 1}

p(|x|)

L = {x |∃y

∈ A ∀ y

∈ A ∃ y

∈ A... Qy

∈ A :(x, y

,...,y

) ∈ L



} .

The quantiﬁer Q is chosen to be an existential or universal quantiﬁer in such

a way that the sequence of quantiﬁers is alternating.

10.4 The Polynomial Hierarchy 135

Proof. We prove the theorem by induction on k.Fork = 1 the statement was

already proven in Theorem 5.3.2. Now suppose we have a representation of

L of the type described for some k ≥ 2. A nondeterministic algorithm can

nondeterministically generate y

∈ A. We allow the algorithm to access as

oracle the decision problem

∗

:= {(x, y

) |∃y

∈ A ∀ y

∈ A... Qy

∈ A :(x, y

,...,y

) ∈



} .

Recall that Q is the quantiﬁer that makes the sequence of quantiﬁers alternate.

Since L ∈

P implies that

L ∈ P, by the inductive hypothesis L

∗

∈ Σ

k−1

.The

nondeterministic algorithm queries the oracle L

∗

about (x, y

) and reverses

the answer. If x ∈ L, then there is some y

∈ A such that

∀ y

∈ A ∃ y

∈ A... Qy

∈ A :(x, y

,...,y

) ∈ L



is true. Therefore, (x, y

) /∈ L

∗

, and the nondeterministic algorithm accepts

x.Ifx/∈ L, then by DeMorgan’s laws for all y

∈ A,

∃ y

∈ A ∀ y

∈ A... Qy

∈ A :(x, y

,...,y

) /∈ L



holds. So (x, y

) ∈ L

∗

for all y

∈ A, and the nondeterministic algorithm does

not accept x on any path. The runtime is polynomially bounded since y

has

polynomial length.

Now suppose L ∈ Σ

.ThenL has a nondeterministic polynomial-time

bounded algorithm A

with oracle L



∈ Σ

k−1

. By the inductive hypothesis

there is a decision problem B ∈

P such that



= {z |∃y

∈ A ∀ y

∈ A... Qy

∈ A :(z, y

,...,y

) ∈ B} .

There are two polynomials q and r such that the algorithm A

on input x

queries the oracle L



at most q(|x|) times with queries of length at most r(|x|).

We can easily modify A

and L



so that on every computation path for every

input z of length |x| exactly q(|x|) queries are made, each of length r(|x|).

Then x ∈ L if and only if there is an accepting computation path w with

corresponding oracle queries b

,...,b

q(|x|)

and oracle answers a

,...,a

q(|x|)

We want to express this in a quantiﬁed expression of the desired form.

The quantiﬁed expression begins

∃ w, b

,...,b

q(|x|)

,...,a

q(|x|)

Let C

∗

be the set of all (x, w, b

,...,b

q(|x|)

,...,a

q(|x|)

), such that

• the ith query of A

on input x along the computation path w is b

if the

previous queries are b

,...,b

i−1

and the answers received are a

,...,a

i−1

;

and

• x is accepted along this path.

136 10 Additional Complexity Classes

Clearly C

∗

∈ P. It remains to check whether the answer a

is the correct

answer to query b

.Ifa

= 1, then we can check this answer via the formula

∃ y

∈ A ∀ y

∈ A... Qy

∈ A :(b

,...,y

) ∈ B.

If a

= 0, then we can check this answer via the formula

∀ y

∈ A ∃ y

∈ A... Qy

∈ A :(b

,...,y

) ∈

Since a

is not known in advance, we must combine both of these cases allowing

the decision problem access to a

∃ y

∈ A ∀ y

∈ A... Qy

∈ A :(b

,...,y

) ∈ B

∗

where B

∗

contains all vectors with a

=1and(b

,...,y

k−1

) ∈ B,andall

vectors with a

=0and(b

,...,y

) ∈

B. Here we see that the case a

increases the number of quantiﬁer alternations by 1. Now we can bring all

these statements together. The ﬁrst existential quantiﬁer is over w and all

, 1 ≤ i ≤ q(|x|). The following universal quantiﬁer is over all y

, 1 ≤

i ≤ q(|x|). This continues until the kth quantiﬁer. Finally, the decision problem

B contains all (x, w, b

,...,y

,...,b

q(|x|)

,...,y

q(|x|)

)with

(x, w, b

,...,b

q(|x|)

,...,a

q(|x|)

) ∈ C

∗

and (b

,...,y

) ∈ B

∗

, 1 ≤ i ≤

q(|x|). So B



∈ P. Now it is only a technical detail to make sure that behind

each quantiﬁer there is a Boolean variable vector of the same polynomial

length p



(|x|). 

Using DeMorgan’s laws we obtain the following corollary.

Corollary 10.4.4. A decision problem is in Π

if and only if there is a poly-

nomial p and a decision problem L



∈ P such that if we let A = {0, 1}

p(|x|)

then

L = {x |∀y

∈ A ∃ y

∈ A... Qy

∈ A :(x, y

,...,y

) ∈ L



} . 

Hereisasummaryoftheresultswehaveachieved:

The complexity classes Σ

and Π

contain problems that can be de-

scribed with k−1 quantiﬁer alternations, polynomially many variables,

and a polynomial-time decidable predicate. They diﬀer in the type of

the ﬁrst quantiﬁer. The hypothesis that these classes are all diﬀerent is

the hypothesis that each new quantiﬁer increases the descriptive power

of such formulas and that it matters which type of quantiﬁer is used

ﬁrst.

This logical perspective simpliﬁes the proof of the following results.

Theorem 10.4.5. If Σ

= Π

, then PH = Σ