Wegener I. Complexity Theory. Exploring the Limits of Efficient Algorithms

Подождите немного. Документ загружается.

7.2 Pseudo-polynomial Algorithms and Strong NP-completeness 95

We call an algorithm for a large number problem pseudo-polynomial if for

every polynomial p(n) the algorithm runs in polynomial time on all inputs

in which all numbers are natural numbers with size bounded by p(n). Under

the assumption that

NP = P, a pseudo-polynomial algorithm implies that a

problem is not strongly

NP-complete. From an algorithmic point of view, this

can be expressed as follows:

NP = P, then problems that are strongly NP-complete do not even

have pseudo-polynomial algorithms.

From this vantage point, it is worth taking another look at the proof of

Theorem 6.3.1, i.e., at the proof that the special knapsack problem

SubsetSum

is NP-complete. For the reduction of 3-Sat to SubsetSum for instances of 3-Sat

with inputs with m clauses and n variables we formed instances of SubsetSum

with decimal length n+m. These are enormous numbers. A polynomial reduc-

tion that used only numbers with size bounded by some polynomial p(n, m)

would imply that

NP = P since by Theorem 7.2.3, SubsetSum is polynomially

solvable when restricted to small numbers.

BinPacking is NP-complete even when restricted to two bins, but is pseudo-

polynomially solvable using the pseudo-polynomial algorithm for

SubsetSum.

Somewhat more generally it can be shown that bin packing problems with

a ﬁxed number of bins are pseudo-polynomially solvable, and therefore not

strongly

NP-complete unless NP = P. Now we consider the other extreme

case of bin packing. Suppose there are n =3k objects, k bins of size b,and

that the sizes of the objects a

,...,a

are such that b/4 <a

<b/2and

+ ···+ a

= k · b. This means that any two objects ﬁt into a bin, but more

than three never do. Now we must decide if the objects can be packed into

k bins. If so, then each of the k bins contains exactly three objects, so this

problem is called 3-

Partition. In contrast to the bin packing problems with

few bins and many objects per bin, this problem with many bins and at most

three objects per bin is strongly

NP-complete.

Theorem 7.2.4. 3-

Partition is strongly NP-complete. 

We will omit the technically involved proof (see Garey and Johnson

(1979)), in which 3-

DM is ﬁrst reduced to 4-Partition with polynomially

large numbers and then this problem is reduced to 3-

Partition with poly-

nomially large numbers. The problem 4-

Partition is deﬁned analogously to

Partition with b/5 <a

<b/3andn =4k. Both polynomial reductions are

interesting since in each case information is coded into numbers, as was the

case in the proof that

3-Sat ≤

SubsetSum. The problem 3-Partition plays

an important role as a starting point in proving that many other problems

are strongly

NP-complete. We will demonstrate this using BinPacking and

the scheduling problem

SWI (sequencing with intervals) as examples.

96 7 The Complexity Analysis of Problems

Theorem 7.2.5. BinPacking and SWI are strongly NP-complete.

Proof. The claim for

BinPacking is clear, since 3-Partition is a special case

BinPacking. To prove the claim for SWI, we ﬁrst describe a polynomial

reduction from 3-

Partition to SWI and then discuss the size of the numbers

used in the reduction. An instance of 3-

Partition consists of numbers n =3k,

b,anda

,...,a

such that b/4 <a

<b/2anda

+ ···+ a

= k · b.Fromthis

we construct an instance of

SWI with n tasks A

,...,A

which represent the

n objects of the instance of 3-

Partition,andk − 1 forcing tasks F

,...,F

k−1

The tasks A

may be started immediately (r(A

) = 0), their duration reﬂects

the size of the corresponding objects (l(A

)=a

), and they must be completed

by time d(A

)=kb+ k − 1. The forcing tasks are deﬁned by r(F

)=ib+ i− 1,

l(F

) = 1, and d(F

)=ib + i. The time of their processing is forced, together

they require k − 1 time, and they force the tasks A

,...,A

to be completed

within k blocks of length b. So there is a packing of the n objects into the

k bins if and only if the n + k − 1 tasks can be completed by one processor

subject to the side conditions.

The largest number that appears in the instance for

SWI is kb + k − 1. If

the numbers in the input for 3-

Partition are bounded by a polynomial p(n),

then b ≤ p(n)andkb + k − 1 ≤ k · (p(n) + 1). So the strong

NP-completeness

SWI follows from the strong NP-completeness of 3-Partition. 

7.3 An Overview of the NP-completeness Proofs

Considered

In the course of the last four chapters we have encountered many reductions,

most of which have been polynomial reductions that have been used to prove

the

NP-completeness or even the strong NP-completeness of the decision vari-

ants of important problems. These results are summarized in Figure 7.3.1.

Here we use

NP(p(n)) to denote all decision problems that can be decided

in nondeterministic time O(p(n)) by an oblivious Turing machine with one

tape. Strongly

NP-complete problems with large numbers are boxed. Poly-

nomial reductions are represented by downward arrows. Next to the arrows

we give the resources required by the reduction: ﬁrst the computation time

and then the size of the instance constructed by the reduction. For clarity we

have omitted the O(·) in each case. So, for example, our reduction of

3-Sat

to DHC applied to a Boolean formula with n variables in m clauses runs in

time O(n + m) and produces an instance of

DHC with O(n + m) vertices and

O(n+ m) edges. For

Sat, l refers to the length of the input. We have also used

some additional abbreviations:

CP for Championship, VC for VertexCover,

SC for SetCover,andKP for Knapsack.

Figure 7.3.1 shows only a tiny piece of the much larger picture of known

NP-

completeness proofs. This diagram represents only those problems that have

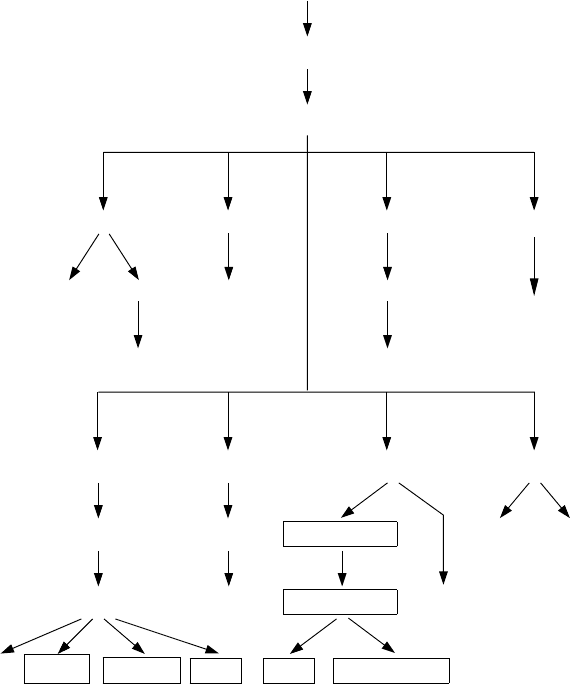
7.3 An Overview of the NP-completeness Proofs Considered 97

DHP

3-GC

BMST

3-DM SubsetSum

4-Partition

3-Partition

SWI BinPacking

n, nn, n

DHC

TSP

2,,sym

TSP



TSP

sym

TSP

k-Sat, k ≥ 3

n + m,

3-4-

(n + m, n + m)

k-GC,

k ≥ 3

MAX-k-Sat,

k ≥ 3

TSP

l, l

Clique

IndependentSet

l, l

n + m,

n + m, n + m,

n + m,

(n + m)

,n + m,

Sat

(p(n))

(n + m, n + m)(m, m

)

n + m

(n + m, n + m)

(n, n + m)

(n + m, n + m)(n + m, n + m) n + m

Partition

(n + m, m)

)(n, n

)

n, nn, n

n + m,

(n, m)

(0,1,3)-

CPn + m,

(n, m)

p(n)

,p(n)

(0,1,3)-

3 rounds

(n + m, m)

n + m, n + m,

n, (n, n)

Fig. 7.3.1. An overview of NP-complete and strongly NP-complete problems.

been discussed here. The full picture of what is known about NP-completeness

would be practically impossible to make: it would ﬁll a large book by itself and

we can safely assume that it would require updating nearly every day. Thus

it was rather an understatement when we spoke in Chapter 1 of thousands of

NP-complete problems.

The full picture of

NP-complete and NP-equivalent problems is im-

mense. The

NP = P-problem is a great intellectual challenge with far-

reaching consequences.

The Complexity of Approximation Problems –

Classical Results

8.1 Complexity Classes

To this point we have understood optimization as a sharply deﬁned criterion:

Only the computation of a provably optimal solution counts as success, ev-

erything else is a failure. In cases where we can compute exact solutions to

optimization problems, we should do so. But many optimization problems are

NP-equivalent. For these problems, if we could eﬃciently compute solutions

with values that are guaranteed to be at least close to the optimal value, this

would be a good way out of the (conjectured)

NP = P-dilemma. This is espe-

cially true for problems from real applications where the parameters are based

on estimates, since exact optimization under these conditions is a ﬁction.

For a decision problem A we will use

Max-A or Min-A to denote the related

optimization problem. We are interested in optimization problems such that

for each instance x there is a non-empty set S(x)ofsolutions and each solution

s ∈ S(x) has a positive value v(x, s) with respect to x. These conditions are

met by the optimization problems we have encountered with the exception

that sometimes solutions have a value of 0, for example an empty set of nodes

for

Clique or VertexCover representing a graph with no edges. In the ﬁrst

case we can simply remove the empty set from the set of solutions S(x), since

there is always a trivial solution that is better, namely a clique of size 1. In the

second case we can exclude graphs with no edges from consideration without

signiﬁcantly altering the problem. We insist that v(x, s) > 0sothatwecan

divide by v(x, s).

Our goal is to compute good solutions s ∈ S(x) and their values v(x, s)

in polynomial time. So we will require that for some polynomial p, the length

of every solution s ∈ S(x) and its value v(x, s) be bounded by p(|x|). For

most problems the values of the solutions will be integers; one exception is

the traveling salesperson problem

Min-TSP

d-Euclid

. Finally, we must decide if

we are interested in a solution with as large a value as possible (maximization

problems) or in a solution with as small a value as possible (minimization

problems). The goodness of a solution s ∈ S(x) should measure “how close”

100 8 The Complexity of Approximation Problems – Classical Results

the value of the solution v(x, s) is to the value of an optimal solution v

opt

(x)

for the instance x. This idea is well-motivated, but it also has the problem

that the deﬁnition contains the unknown value v

opt

(x). If we could compute

opt

(x) eﬃciently, then the underlying evaluation problem would be solvable

in polynomial time. As we saw in Section 4.2, for most problems this implies

that the optimization problem itself is solvable in polynomial time. So we will

be forced to estimate v

opt

(x).

But ﬁrst we want to formalize how we will measure the “closeness”

of v(x, s)tov

opt

(x). The most obvious idea is to consider the diﬀerence

opt

(x)−v(x, s), or its absolute value. But in many cases this is inappropriate.

A diﬀerence of 10 between a computed solution and an optimal solution for

Min-BinPacking is awful if 18 bins suﬃce, but it is respectable when 1800

bins are needed. For

Min-TSP the problem is changed formally, but not sub-

stantially, when we express the distances in meters instead of kilometers. The

same is true if we express the utility of objects in the knapsack problem using

monetary units and switch from dollars to cents. In both cases the diﬀer-

ence v

opt

(x)− v(x, s) would increase by a constant factor. That this diﬀerence

should provide a good measure of the goodness of a solution is the exception

rather than the rule. So instead we will use the usual measure of goodness,

namely the ratio of v

opt

(x)tov(x, s). The diﬃculties discussed above in our

consideration of v

opt

(x) − v(x, s) do not arise. We follow the tradition of us-

ing the quotient v

opt

(x)/v(x, s) for maximization problems and the quotient

v(x, s)/v

opt

(x) for minimization problems. This ensures that we obtain uni-

form values of goodness that always have a value of at least 1. But we have

to accept that better solutions have a smaller goodness than worse solutions.

This deﬁnition is always used for minimization problems. For maximization

problems, the quotient v(x, s)/v

opt

(x) can also be found in the literature.

Deﬁnition 8.1.1. For optimization problems the approximation ratio r(x, s)

for a solution s for instance x is deﬁned by

• v

opt

(x)/v(x, s) for maximization problems, and

• v(x, s)/v

opt

(x) for minimization problems.

For an optimization algorithm A we expect that for each instance x a

solution s

(x) is computed, which will then have an approximation ratio of

(x):=r(x, s

(x)). For ε := ε

(x):=r

(x) − 1, such a solution is called

ε-optimal. For minimization problems the value of the computed solution is

100 · ε % above the optimal value, and for maximization problem the optimal

valueis100· ε % larger than the value of the computed solution, the value of

which is 100 · (ε/(1 + ε)) % smaller than the optimal value. Just as we do not

consider the computation time t

(x) of an algorithm for each input, instead

of r

(x) we will investigate the worst-case approximation ratio

(n):=sup{r

(x): |x|≤n} .

8.1 Complexity Classes 101

Sometimes the worst-case approximation ratio is not the best measure. For

example, in Section 8.2 an eﬃcient approximation algorithm A for

BinPacking

is presented for which

v(x, s

(x)) ≤

· v

opt

(x)+4.

Thus

(x) ≤

opt

(x)

Since v

opt

(x) ≥ 1, it follows that r

(n) ≤ 47/9. Since we can eﬃciently rec-

ognize instances where all the objects ﬁt into a single bin, we only need the

estimate for the case that v

opt

(x) ≥ 2, which leads to r

(n) ≤ 29/9. For in-

stances with large values of v

opt

(x), however, this approaches the much better

approximation ratio of 11/9. Therefore we use the notation r

∞

(asymptotic

worst-case approximation ratio) to denote the smallest number b such that

for every ε>0 there is a value v(ε) such that for all x with v

opt

(x) ≥ v(ε)

the relation r

(x) ≤ b + ε holds. We will see that (under the assumption that

NP = P) there are problems for which the smallest asymptotic worst-case ap-

proximation ratio achievable in polynomial time is smaller than the smallest

worst-case approximation ratio achievable in polynomial time.

An approximation problem is an optimization problem for which we do not

necessarily demand the computation of an optimal solution but are satisﬁed to

achieve a prescribed (perhaps asymptotic) approximation ratio in polynomial

time. This raises the question of determining the complexity of approximation

algorithms. We can also ask at what point (for what approximation ratio) the

complexity switches from “

NP-equivalent” to “polynomially solvable”. When

we considered optimization problems, we were able to restrict our attention

to the treatment of their decision problem variants. Approximation problems

have reasonable variants as evaluation problems: In the case of maximization

problems, we can require that a bound b be computed so that the value of the

optimal solution lies in the interval [b, b · (1 + ε)]; for minimization problems

the optimal value should be in the interval [b/(1+ε),b]. There is not, however,

any meaningful decision variant for an approximation problem. For inputs x

with v(x, s) ≤ b for all s ∈ S(x), the question of whether the value of an

optimal solution to a maximization problem lies in the interval [b, b · (1 + ε)]

requires a statement about the value of an optimal solution.

Our deﬁnitions allow trivial solutions. For example, for

Clique an algo-

rithm can always output a single vertex as a clique of size 1. The result is an

approximation ratio of at most n. If instead we consider all sets of vertices of

size at most k, checking them in polynomial time to see which ones form a

clique, and outputting the largest clique found, we are guaranteed an approx-

imation ratio of n/k. Approximation ratios become interesting when they are

not “trivially obtainable”.

102 8 The Complexity of Approximation Problems – Classical Results

Deﬁnition 8.1.2. Let r : N → [1, ∞) with r(n +1)≥ r(n) be given.

• The complexity class

APX(r(n)) contains all approximation problems which

can be solved by a polynomial-time algorithm A with a worst-case approx-

imation ratio of r

(n) ≤ r(n).

• We let

APX denote the union of all APX(c) for c ≥ 1.

• We let

APX

∗

denote the intersection of all APX(c) for c>1.

APX is the class of all approximation problems that can be solved in poly-

nomial time with some constant maximal approximation ratio. The deﬁnition

APX

∗

requires an APX(c) algorithm for each c>1. This does not, however,

imply the existence of an algorithm which given an ε>0 computes an ε-

optimal solution. Such an algorithm would have the advantage that its users

could choose for themselves the approximation ratio they desired.

Deﬁnition 8.1.3. A polynomial-time approximation scheme (abbreviated

PTAS) for an approximation problem is an algorithm A that takes an in-

put of the form (x, ε), where x is an instance of the approximation problem

and ε>0 is a rational number, and for a ﬁxed ε produces in polynomial time

(with respect to the length of x) a solution with worst-case approximation ratio

at most 1+ε. The complexity class

PTAS contains all optimization problems

for which there is a polynomial-time approximation scheme.

Even with a PTAS we have not satisﬁed all our wishes. Runtimes of

Θ(n

1/ε

)orΘ(n · 2

1/ε

) are allowed, since for a constant ε these are poly-

nomially bounded. But for small values of ε, these runtimes are not tolerable,

in contrast to runtimes of, for example, Θ(n/ε).

Deﬁnition 8.1.4. A fully polynomial-time approximation scheme (abbrevi-

ated FPTAS) is a PTAS for which the runtime is polynomially bounded with

respect to the length of x and the value of 1/ε. The complexity class

FPTAS

contains all optimization problems for which there is a fully polynomial-time

approximation scheme.

If we restrict

P to optimization problems, then

P ⊆ FPTAS ⊆ PTAS ⊆ APX .

For optimization problems which presumably do not belong to

P,wearein-

terested in determining whether they belong to

FPTAS, PTAS, or at least to

APX. In the case of APX, we are interested in ﬁnding as small a c as possible

so that the problem belongs to

APX(c). For still more diﬃcult problems we

are interested in slowly growing functions r so that the problems belong to

APX(r(n)). There is an obvious generalization of these classes from determin-

istic algorithms to randomized algorithms, but this will not be described in

detail here.

8.2 Approximation Algorithms 103

Approximation algorithms that run in polynomial time for diﬃcult op-

timization problems form a relevant alternative for applications. Com-

plexity classes are available to diﬀerentiate which approximation ratios

are achievable.

8.2 Approximation Algorithms

In order to get a feel for approximation algorithms a few examples of eﬃcient

approximation algorithms are discussed here, although for many proofs we

will merely give pointers to textbooks on eﬃcient algorithms. In addition, a

number of approximation results will be cited. We will start with approxima-

tion ratios that grow with the size of the instance and then continue with

APX

algorithms, PTAS, and FPTAS.

We begin with two problems for which methods from Chapter 12 suﬃce

to show that they do not belong to

APX if NP = P.ForMax-Clique an ap-

proximation ratio of O(n/log

n) can be obtained (Boppana and Halld´orsson

(1992)). This is only a minor improvement over the trivial approximation ra-

tio of n or εn for arbitrary ε>0. For the covering problem

Min-SetCover

it is also trivial to obtain an approximation ratio of εn. Here, however, it

was possible to achieve in polynomial time an approximation ratio of O(log n)

(Johnson (1974)).

We will now present

APX algorithms for a few problems. How good their

approximation ratios are will be discussed in Section 8.3 and in Chapter 12.

Our ﬁrst example is

Min-VertexCover. We will use a simple “pebbling al-

gorithm” in which we imagine placing pebbles on the vertices of the graph as

the algorithm proceeds. At the start of the algorithm, none of the vertices

are pebbled. In linear time we can traverse the list of edges and select an edge

if both of its vertices are still unpebbled. These two vertices are then pebbled.

The algorithm continues until there are no more edges that can be selected;

the output consists of the set of pebbled vertices. If the pebbled vertices did

not cover the edge {v, w}, then this edge could have been selected, so the peb-

bled vertices form a vertex cover of the edges. If k edges are selected, then the

vertex cover contains 2k vertices. The k edges have no vertices in common, so

at least k vertices are needed just to cover those edges. So we have obtained

an approximation ratio of 2.

The following interesting algorithm for

Max-3-Sat achieves an approxi-

mation ratio of 8/7 if all the clauses have exactly three diﬀerent literals. For

each clause c

there are 8 possible assignments for its three variables, and

seven of these satisfy the clause. Let X

be the random variable that takes

on the value 1 if a random variable assignment satisﬁes the clause c

and 0

otherwise. By Remark A.2.3, E(X

)=Prob(X

=1)=7/8; and by Theo-

rem A.2.4 for m clauses if we let X := X

+ ··· + X

,thenwehavethe

equation E(X)=(7/8) · m. So on average, (7/8) · m clauses are satisﬁed, but

never more than m. So a random variable assignment has an approximation

104 8 The Complexity of Approximation Problems – Classical Results

ratio of at most 8/7. Now we will derandomize this algorithm. For this we

investigate the two possible values of the Boolean variable x

, i.e., x

=0or

= 1. It is simple to compute E(X | x

= b)forb ∈{0, 1} as a sum of all

:= E(X

| x

= b). Thus a

= 1 if the clause is satisﬁed by x

= b, a

=7/8

if the clause still has three unassigned variables, a

=3/4 if the clause still has

two unassigned variables and the third literal has the value 0. In the course

of this procedure there will be clauses with one unassigned variable and two

literals with the value 0. Then the respective conditional expected value is

1/2. Finally, the conditional expected value of X

is 0 if all three literals have

already been assigned “false”. By Theorem A.2.9 we have

E(X)=

· E(X | x

=0)+

· E(X | x

=1),

and there is a value b

∈{0, 1} such that

E(X | x

= b

) ≥ (7/8) · m.

Since we have computed both conditional expected values, we can choose b

suitably. Now we continue analogously for the two possible values of x

n−1

.In

the end we will have found b

,...,b

∈{0, 1} with E(X | x

= b

,...,x

) ≥ (7/8) · m. This condition ﬁxes the values of all the variables, and X

is the number of clauses satisﬁed in this way. The runtime is O(nm), since

for each variable x

we consider the clauses that result from setting x

i+1

,...,x

= b

For

Min-BinPacking it is very simple to obtain an approximation ratio of

2. We pack each object in order into a bin, using a new bin only if it does

notﬁtintoanyofthebinsalreadyused.Ifalltheobjectsﬁtintoonebin,we

obtain the optimal solution. Otherwise, let b

∗

be the size of the contents of the

least packed bin. If b

∗

≤ b/2, then by our strategy all the other bins are ﬁlled

with contents at least b − b

∗

. So on average, the bins are always ﬁlled at least

half-way, thus it is impossible to halve the number of bins used. A somewhat

more complicated algorithm achieves in polynomial time an approximation

ratio of 3/2. Here we notice that the larger objects cause special problems.

That leads to the following idea. First the objects are sorted by size, and the

larger objects are packed ﬁrst. Each object is packed into the bin with the

smallest amount of free space that can still hold the object. The resulting

strategy is referred to as “best-ﬁt decreasing” (BFD). For this algorithm the

relation

v(x, s

BFD

(x)) ≤

opt

(x)+4

was proved (Johnson (1974)). As was already discussed in Section 8.1, this

leads to an upper bound for the asymptotic worst-case approximation ratio of

11/9. A polynomial algorithm of Karmarkar and Karp (1982) has an approx-

imation ratio bounded by 1 + O((log

opt

(x))/v

opt

(x)), i.e., an asymptotic

worst-case approximation ratio of 1. This kind of algorithm is also called

8.2 Approximation Algorithms 105

an asymptotic FPTAS. In Section 8.3 and Chapter 12 we will discuss lower

bounds for worst-case approximation ratios of polynomial-time algorithms.

Two results for traveling salesperson problems should be brieﬂy men-

tioned. For

Min-TSP



a worst-case approximation ratio of 3/2 can be guar-

anteed by a polynomial-time algorithm (see Hromkoviˇc (1997)), and for

Min-TSP

d-Euclid

there is even a PTAS (Arora (1997)). For Min-VertexCover

and Max-IndependentSet there is also a PTAS if we require that the graphs

be planar (Korte and Schrader (1981)).

We will demonstrate the construction of a PTAS using as an example a

simple scheduling problem for which even an FPTAS is known. The problem

consists of scheduling n tasks on two processors in such a way that the maximal

load of the processors is minimized. The processors are identical and require

time a

for the ith task. The basic idea is that the most important thing is

to schedule the “large tasks” (those for which a

is large) well, and that there

cannot be all that many large tasks. Let ε>0 be given and let L := a

+···+a

be the total time required for the n tasks. A task will be considered large if

it requires time at least εL. Then the number of large tasks is bounded by

the constant 1/ε and there are “only” at most c := 2

1/ε

distributions of

these large tasks between the two processors. For each of these c distributions

the remaining tasks are scheduled “greedily”, that is each task is assigned

to the processor with the lightest load. From among the at most c solutions

that result, the best one is chosen. The required computation time of O(nc)

is linear for a constant ε, but it is not a polynomial in n and 1/ε.Wenow

compare the maximal load in an optimal solution with the maximal load from

the approximation algorithm. The optimal solution also distributes the large

tasks between the two processors, and we consider the attempted solution of

the approximation algorithm that begins by distributing the large tasks in

exactly the same way. If all the smaller tasks can be handled by the processor

with the lesser load after assigning the large tasks without increasing its load

beyond the load of the other processor, then the approximation algorithm

provides an optimal solution. Otherwise, the greedy algorithm ensures that

the load of the two processors diﬀers by at most εL. Thus the larger load is at

most εL/2 larger than the load of both processors if they are equally loaded.

If the loads are equally distributed, the load for each processor is L/2. For an

instance x, v

opt

(x) ≥ L/2andv(x, s) ≤ L/2+εL/2 = (1 + ε)L/2. Thus the

solution is ε-optimal and we have designed a PTAS.

Finally, we want to discuss the ideas for an FPTAS for

Max-Knapsack

(see also Hromkoviˇc (1997)). In the proof of Theorem 7.2.3 we presented a

pseudo-polynomial time algorithm for

Knapsack using the method of dynamic

programming. This algorithm was polynomially time-bounded in the case that

the weights were polynomially bounded. In a similar fashion it is possible to

design a pseudo-polynomial time algorithm that is polynomially time-bounded

for polynomially bounded utility values and arbitrary weights. Now consider

an arbitrary instance x of

Max-Knapsack. We can assume that w

≤ W

for each object i. If we alter the utility values, we do not change the set of