Wegener I. Complexity Theory. Exploring the Limits of Efficient Algorithms

Подождите немного. Документ загружается.

84 6 NP-complete and NP-equivalent Problems

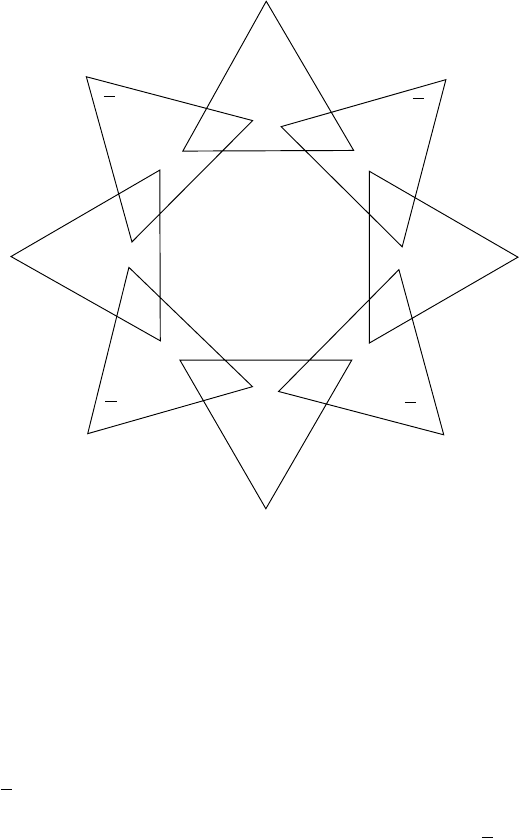
Fig. 6.6.1. A selection component from the reduction 3-Sat ≤

3-DM.

with the interpretation that x

= 0, or we choose T

, T

,andT

with the

interpretation that x

= 1. It is also clear from Figure 6.6.1 that this method

would not work if we had only two groups of experts.

For the jth clause c

,wehaveapersonp

in group 2 and a person p

in group 3. These two people can only be in a team together, and need a

third member from group 1, which is intended to represent the satisfaction

of one of the literals occurring in c

. If the literal x

occurs in c

, then there

is a team (x

). There are enough people for each literal so that each

(or

) only occurs in one team. Finally, there are people q

and q

for

1 ≤ j ≤ 2m, designed to form teams with the remaining people of group 1.

These people are very ﬂexible, and all triples (x

)and(

) form

potential teams.

Satisfying assignments lead to a formation of teams such that the selection

components do not integrate the people representing the satisﬁed literals. So

and p

ﬁnd a third team member and then teams are formed with q

and

. On the other hand, any formation of teams on the selection components

can be translated into a variable assignment. If all p

and p

belong to teams,

then the variable assignment is satisfying. 

6.7 Championship Problems 85

An important generalization of 3-DM is the set cover problem, SetCover,

in which a set S,anumberk and a sequence A

,...,A

of subsets of S are

given and we must decide whether S is the union of k of the subsets A

An important application area is the minimization of depth-2 circuits. If we

let S be the set of all people in an instance of 3-

DM, and form a 3-element

subset of S for each potential team, then we obtain a polynomial reduction

DM ≤

SetCover.Thatis,

Corollary 6.6.2.

SetCover is NP-complete. 

6.7 Championship Problems

We have already seen that the championship problem with the (0, 1, 2)-

partition rule can be solved in polynomial time. With the introduction of the

(0, 1, 3)-partition rule in the mid-1990’s, the complexity theoretic investiga-

tion of this problem became interesting. The complexity of the championship

problem changes dramatically with this new point rule.

Theorem 6.7.1. The championship problem with the (0,1,3)-partition rule is

NP-complete.

Proof. Once again we will use

3-Sat as the starting point for our reduction.

For the championship problem we will use another representation. We let the

selected team win all its games and temporarily let all other games end in

a tie. The other teams will be represented by vertices and labeled with a

number z ∈ Z indicating that after these temporarily assigned outcomes the

team has z more points than the selected team. The games that remain to be

played are represented by edges between the opposing teams. The question

is now whether the temporarily assigned outcomes can be modiﬁed in such

a way that all vertices are labeled with non-positive values. At each edge,

the outcome may be changed once. The eﬀect is that one team receives two

additional points, and the other team loses a point, since a 1:1 tie is converted

into a 3:0 victory for one team.

Now let an instance of

3-Sat be given, i.e., clauses c

,...,c

over variables

,...,x

. We begin with the construction of variable components that are

to reﬂect the assignment x

=0orx

= 1. Variables that do not occur will

be ignored. For all other variables x

, we form a binary tree in which the

left subtree has as many leaves as there are occurrences of x

in c

,...,c

Similarly the right subtree will have as many leaves as there are occurrences

. The root is labeled +1, the leaves are labeled −2, and the other vertices

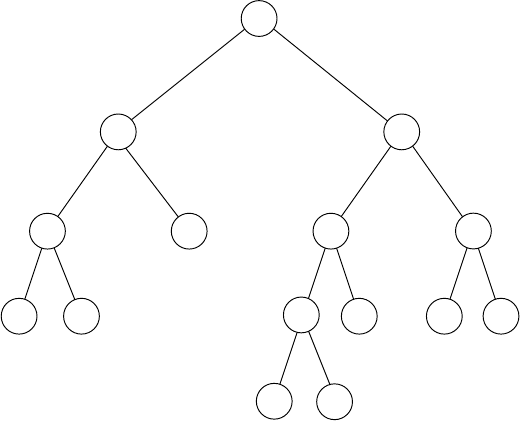
are labeled 0. Figure 6.7.1 shows an example.

Only the teams at the leaves will play additional games. In order to achieve

a non-positive label, the root team must lose the game to one of its two

children, and we will interpret a loss to the left child as x

= 0 and a loss to

the right child as x

= 1. If the root loses to its right child, then the child

86 6 NP-complete and NP-equivalent Problems

−2

−2 −2

−2

Fig. 6.7.1. A variable component from the reduction 3-Sat ≤

(0, 1, 3) −

Championship. In this example x

occurs positively in three clauses and negatively

in ﬁve clauses.

receives a value of +2, and must therefore lose to both of its children, ....This

domino eﬀect continues down to the leaves, which obtain the value 0. At this

point, only the leaves in the left subtree (which represents x

= 1) can still

gain points. The construction of the clause components and the connections

to the variable components are now obvious. The clause components consist

of a single node (team) labeled +1. This team has three games to play, one

for each of its literals. If the clause contains the literal x

, then the team

must play one of the leaves of the x

component in the subtree representing

= 1. Of course, this is done in such a way that each leaf must play exactly

one more game. This completes the construction of an instance of (0, 1, 3)-

Championship.WehaveO(m) teams and O(m) games. The construction can

be carried out in time O(m).

From a satisfying assignment a for all of the clauses, we obtain the fol-

lowing modiﬁcations to the temporarily assigned game outcomes which result

in the selected team becoming league champion. The roots of the variable

components start the domino eﬀect that corresponds to their assigned value.

Then, for each clause component there is still one game against a team that

represents a satisﬁed literal and can therefore receive two additional points.

This game is lost by the team representing the clause. On the other hand,

game outcomes that produce a championship for the selected team must use

at least one of the two subtrees of each variable component in order to reduce

the excess points at the root. We interpret this as the variable assignment.

6.7 Championship Problems 87

The assignment must satisfy all the clauses since otherwise a clause compo-

nent cannot reduce its excess points. 

From this example we see that problems that do not belong to the typical

repertoire of combinatoric optimization but come from decisions made by

soccer functionaries can also be handled using the means of complexity theory.

Many very diﬀerent-looking problems with direct or at least indi-

rect connections to real applications prove to be

NP-complete or NP-

equivalent. The proofs for

NP-completeness use special features of the

problems being considered but otherwise follow a common outline. One

can therefore hope that proofs of

NP-completeness for new problems

can be obtained “almost routinely”. Of the problems we have consid-

ered so far, only the graph isomorphism problem GraphIsomorphism

cannot be assigned one of the two categories “polynomially solvable”

and “

NP-equivalent”.

The Complexity Analysis of Problems

7.1 The Dividing Line Between Easy and Hard Versions

of a Problem

We now return to the families of problems introduced in Section 2.2. We will

use these examples to investigate just where the dividing line between easy

and hard problems runs. To do this we will compare similar-looking problems

such as the two covering problems

VertexCover and EdgeCover, and we will

restrict the set of inputs of general problems like

GC in various ways. Claims

that particular problems are eﬃciently solvable will for the most part be

omitted. Such proofs can be found in textbooks covering eﬃcient algorithms.

We will also omit some of the

NP-completeness proofs.

All the variants of the traveling salesperson problem

TSP that we have

considered are

NP-equivalent. The results of Section 6.2 have interesting im-

plications for two other families of problems. While the problem of computing

a minimum spanning tree can be done eﬃciently by means of Kruskal’s algo-

rithm, this problem becomes

NP-equivalent if we place a bound on the degrees

of the vertices in the desired spanning tree. Similarly, ﬁnding the shortest path

from s to t can be done eﬃciently using Dijkstra’s algorithm, but ﬁnding the

longest cycle-free path from s to t is

NP-equivalent. The hardness of the latter

problems follows from the

NP-completeness of the directed Hamiltonian path

problem

DHP.

SubsetSum and Partition are very specialized knapsack and partitioning

problems that are hard. The hardness of these problems carries over to all

more general variants of these problems. The class of scheduling problems has

an especially rich structure. Various combinations of such parameters as the

number of available processors, the speed of the processors, the suitability

of the processors for speciﬁc tasks, the earliest start times for processing the

tasks, the latest completion times, restrictions on the order in which tasks

must be completed, or the option to interrupt tasks lead to an abundance

of problems of diﬀering complexity. Results about scheduling problems can

90 7 The Complexity Analysis of Problems

be found in Lawler, Lenstra, Rinnooy Kan, and Shmoys (1993), and Pinedo

(1995).

We have seen that the team building problem 2-

DM is solvable in polyno-

mial time, but that 3-

DM (and therefore the problems k-DM for all k ≥ 3) is

NP-complete. With the help of an algorithm for 2-DM we can solve the edge

covering problem

EdgeCover, but the vertex covering problem VertexCover

is NP-complete.

Of the satisﬁability problems, k-

Sat is NP-complete if k ≥ 3, and Max-k-Sat

is NP-complete for k ≥ 2. For Max-k-Sat we need to decide if at least l

of the m clauses can be simultaneously satisﬁed, where l is a part of the

input. So k-

Sat is just the special case that l = m, from which it follows

that

Max-k-Sat is NP-complete for k ≥ 3. The proof that Max-2-Sat is also

NP-complete will not be given here, but this result has implications for the

optimization of pseudo-Boolean functions f : {0, 1}

→ R. Clauses can be

“arithmetized” as follows: a disjunction of literals z

+ z

+ ···+z

is replaced

by 1 − (1 − z

)(1 − z

) ···(1 − z

)and¯x

is replaced by 1 − x

.Ifweadd

the “values” of all the resulting clauses we get a pseudo-Boolean polynomial

f : {0, 1}

→ R with the properties that f(a) is the number of clauses satisﬁed

by the assignment a and the degree of f is bounded by the maximum number

of literals occurring in a single clause. From the

NP-completeness of the deci-

sion variant of

Max-2-Sat it follows that the decision variant of the problem

of maximizing a pseudo-Boolean polynomial of degree 2 is also

NP-complete.

Surprisingly, 2-

Sat is solvable in polynomial time. To see this we transform an

instance of 2-

Sat into a directed graph on the vertices x

, x

,...x

, x

Each clause z

+ z

gives rise to a pair of edges (z

)and(z

), which

represent the implications “z

=0=⇒ z

=1”and“z

=0=⇒ z

= 1”. All

of the clauses can be simultaneously satisﬁed if and only if there is no variable

such that there are paths both from x

and also from x

to x

in the

resulting graph.

Vertex coloring problems have very special hard subproblems. 3-

GC is NP-

complete, and therefore k-

GC is NP-complete for any k ≥ 3. To show that

3-GC ≤

k-GC, we add to the given graph k − 3 additional vertices which are

connected to each other and to each vertex in the original graph. These new

vertices will then require k − 3 colors, and none of these colors may be used

for any of the original vertices. A greedy algorithm solves

2-GC in polynomial

time. We take note of two further restrictions:

• k-d-

GC is the restriction of k-GC to graphs with vertex degree at most d.

• k-

is the restriction of k-GC to planar graphs, i.e., to graphs that can

be embedded in the plane without necessitating crossing edges.

The problem k-d-

results from applying both of the above restrictions

at once. Now we get some problems that are trivial in the sense that in their

decision variants all inputs are accepted. This is the case for k-d-

GC when

k>d, since regardless of how the at most d neighbors of a vertex have been

colored, there will always be a color remaining for the vertex itself. Since the

7.1 The Dividing Line Between Easy and Hard 91

famous “Four Coloring Problem” has been solved, we know that every planar

graph is 4-colorable. Therefore, k-

is trivial for k ≥ 4 and, as we have

previously seen, polynomial time decidable for k ≤ 2. In contrast, the very

special problem 3-4-

is NP-complete. This is the problem of deciding if a

planar graph with maximal degree 4 is 3-colorable. This last claim follows by

composing two polynomial reductions each using local replacement showing

that

3-GC ≤

3-GC

≤

3-4-GC

We begin with an instance G of 3-

GC and an embedding of G in the

plane with crossings. Figure 7.1.1 indicates how we replace an edge with three

crossings. The subgraph P is the planar graph shown in Figure 7.1.2 with

four outer vertices A, B, C,andD. A little experimenting easily shows the

following:

• In every 3-coloring of P , A and C have the same color, and B and D have

the same color.

• Every coloring f of A, B, C,andD with f(A)=f(C)andf(B)=f(D)

can be extended to a 3-coloring of P .



Fig. 7.1.1. Dealing with intersecting edges in 3-GC ≤

3-GC

This construction guarantees that in Figure 7.1.1 the vertices u and u



receive the same color, so u and v must receive diﬀerent colors. On the other

hand, every coloring of the nonplanar graph can be translated into a coloring

of the planar graph.

In the next step a vertex v with degree d>4 is replaced with a planar

graph H

with d “outer” vertices with degree at most 2, and “inner” vertices

with degree at most 4. In addition, this graph will be 3-colorable if and only

if the outer vertices all have the same color. Then the d edges incident to

v can be distributed among the d outer vertices of the graph representing v

without changing the colorability properties. The construction is described in

Figure 7.1.3 for d = 6. Since the vertices 1, 2, and 3 in H

∗

have degree 2, two

copies of H

∗

can be fused at those vertices without increasing the degree of

any vertex beyond 4.

Finally, we handle the championship problem with n teams. With the a-

point rule, this problem is polynomial-time solvable. On the other hand, with

the (0, 1, 3)-point rule, the problem becomes

NP-complete. This result can be

92 7 The Complexity Analysis of Problems

Fig. 7.1.2. The planar graph P .

∗

Fig. 7.1.3. The replacement of a vertex with degree 6 by a planar graph with

maximal degree 4.

generalized to the (0, 1,b)-point rule for any b ∈ Q with b>1andb =2.In

this case, for example, the (0, 1, 3/2)-point rule can be better interpreted as

the (0, 2, 3)-point rule, to which it is equivalent. Actual championship prob-

lems are more speciﬁc than the problems we have dealt with so far. Often

leagues are scheduled in rounds in which each team plays exactly one game.

(0, 1, 3)-

Championship is still NP-complete for three remaining rounds, but

polynomial-time solvable for two remaining rounds. It is not clear, however,

if the given standings can actually be achieved in a league where each team

plays each other twice (once at home and once away). In addition, the German

Soccer League (Fußball Bundesliga), for example, uses a prescribed scheduling

scheme that has strong “locality properties”. Under these conditions, (0, 1, 3)-

Championship is polynomial-time solvable for O(log

1/2

n) remaining rounds.

7.2 Pseudo-polynomial Algorithms and Strong NP-completeness 93

Whether this problem is actually polynomial-time solvable for any number of

remaining rounds is an open problem.

For

NP-complete and NP-equivalent problems, it is worth considering

whether one only needs an algorithm for a specialized problem variant,

and if so to investigate the complexity of this specialized problem. We

have used examples to show that the dividing line between easy and

diﬃcult problems can follow a surprising course.

7.2 Pseudo-polynomial Algorithms and Strong

NP-completeness

In Section 7.1 we did not handle an important possibility for restricting prob-

lems, namely to restrict the size of the numbers that occur in the instances.

We consider here only natural numbers. Inputs with bit length n can contain

numbers that are exponentially large with respect to n. On the other hand,

most applications only require numbers of moderate size.

We are interested here in problems in which numbers that are not bounded

by a polynomial in the input length are still meaningful. For the decision vari-

ant of the clique problem we ask about the existence of a clique of size k,where

k is a parameter of the input. In principal, k can be any natural number. But

the only meaningful values of k are in {2,...,n} since all graphs have cliques

of size 1 and no graphs have cliques of size k>n.So

Clique is not of inter-

est in this discussion. The same is true for all variants of the clique problem,

for covering problems, team building problems, and veriﬁcation problems. On

the other hand, traveling salesperson problems, knapsack problems, partition

problems, network ﬂow problems, championship problems, and number theory

problems of the sort for which the numbers that occur may meaningfully take

on values that are not bounded by a polynomial in the length of the input,

are in principle still meaningful. They are called large number problems.

For diﬃcult problems (e.g.,

NP-equivalent problems) we pose the question:

Are these problems still diﬃcult if the numbers that occur are polynomially

bounded in the length of the input? Number theory problems are a special

case. An instance of

Primes, for example, consists of exactly one number repre-

sented in binary. The value of this number is always exponential in the length

of its binary representation. Thus it is not possible to polynomially restrict the

size of the numbers that occur in instances of

Primes. This situation is diﬀer-

ent for the other problems mentioned above. Because of the great importance

of problems restricted to small numbers, large number problems that remain

diﬃcult when restricted in this way have received a special designation.

Deﬁnition 7.2.1. A large number decision problem A is called

NP-complete

in the strong sense (or, more brieﬂy, strongly

NP-complete) if there is a poly-

nomial p(n) such that the problem is

NP-complete when restricted to instances

94 7 The Complexity Analysis of Problems

where all the numbers that occur are elements of N whose values are bounded

by p(n), where n is the length of the instance.

Theorem 7.2.2. The traveling salesperson problem

TSP and the champi-

onship problem

Championship with the (0, 1,a)-point rule are strongly NP-

complete.

Proof. We already know that

TSP is NP-complete even when the distances

are only allowed to take on values from the set {1, 2}. The largest number

that occurs is then n, the name of the last city.

Championship is NP-complete with the (0, 1, 3)-point rule, and so the num-

bers in the instance are bounded by the number of teams, the number of games

that remain to be played, and the current scores. In our reduction of

3-Sat to

(0, 1, 3)-

Championship in the proof of Theorem 6.7.1, no team plays more than

three additional games, so the largest point diﬀerence that can be made up

is 9 points. Thus (0, 1, 3)-Championship remains NP-complete when restricted

to small numbers. 

Under the assumption that

NP = P, the notion “strong NP-completeness”

can complexity theoretically distinguish among

NP-complete problems.

Theorem 7.2.3. If

NP = P, then Knapsack is not strongly NP-complete.

Proof. The claim will be proved by giving an algorithm for

Knapsack that for

polynomially bounded weight values runs in polynomial time. The algorithm

uses the method of dynamic programming. Consider an instance of

Knapsack

with n objects and weight limit W . We will let KP(k,w)(for1≤ k ≤ n

and 0 ≤ w ≤ W ) denote the modiﬁed instance in which only the ﬁrst k

objects are considered and the weight limit is w.LetU(k, w) be the largest

utility that can be achieved for the instance

KP(k, w), and let D(k, w)bethe

decision for an optimal packing of the knapsack whether we pack object k

(D(k, w) = 1) or do not pack object k (D(k, w) = 0). In addition, we give

reasonable values for extreme values of the parameters: U(k, w)=−∞,if

w<0; and U (0,w)=U(k, 0) = D(k, 0) = 0, if w ≥ 0.

The algorithm now ﬁlls out a table row by row with the values

(U(k, g),D(k, g)). If we are considering

KP(k, w), we can pack object k,win-

ning a utility of u

, and reduce the weight limit for the remaining objects to

w − w

(itispossiblethatw − w

< 0). So we must consider the problem

KP(k − 1,w− w

). If we decide not to pack object k, then we must consider

KP(k − 1,w). So

U(k, w)=max{U(k − 1,w),U(k − 1,w− w

)+u

} .

Furthermore, we can set D(k, w)=1ifU(k − 1,w− w

)+u

≥ U (k − 1,w),

and D(k, g) = 0 otherwise. The computation of (U(k, w),D(k, w)) can be done

in time O(1). The entire runtime amounts to O(n · W ) and is polynomially

bounded if W is polynomially bounded in n. 