Втюрин В.А. Автоматизированные системы управления технологическими процессами
Подождите немного. Документ загружается.


60
Здесь Т постоянная времени [с].
Если выражения (9.4, 9,5.9,6) стоят в знаменателе передаточных функций
звеньев (а, в числителе 1), то звенья называются соответственно
интегрирующим, апериодическим, колебательным. Для колебательного звена z
- безразмерный коэффициент затухания (0 < z < 1). Если выражения стоят в
числителе передаточных функций звеньев, то звенья называются
соответственно дифференцирующим, форсирующим первого порядка,
форсирующим второго порядка.
Для перехода от стандартной формы записи необходимо вычислить
полюса и нули соответствующих типовых звеньев.
Для передаточных функций, использующих выражение (9.4) –
*(0)
0
=
s
, (9.7)
использующих выражение (9.5) –
1
*(0)
= −
s
T
, (9.8)
использующих выражение (9.6) –
2
1
*(0)
1,2
2
ζ ζ
= − ± −s
T T
T
, (9.9)
или
( )
1
*(0)
cos
1,2
= − ζ± ϕ
s i
T
(9.10)
где j = arcsin z .
Коэффициент представления C вычисляется по формуле
0
1
*
1
( )
( )
( )
m
j
j
n
i
i
T
W s
T
=
=
=
∏
∏
, (9.11)
Замечание. Для звеньев, использующих выражение (9.6),
соответствующая постоянная времени входит в выражение (9.11) в квадрате.
При замыкании системы с передаточной функцией W
p
(s) единичной обратной
связью передаточная функция замкнутой системы W
з
(s) принимает вид:
61
p
p
( )
( )
1 ( )
=
±
W s
W s
W s
, (9.12)
где знак “+” соответствует отрицательной обратной связи; знак “–”
соответствует положительной обратной связи.
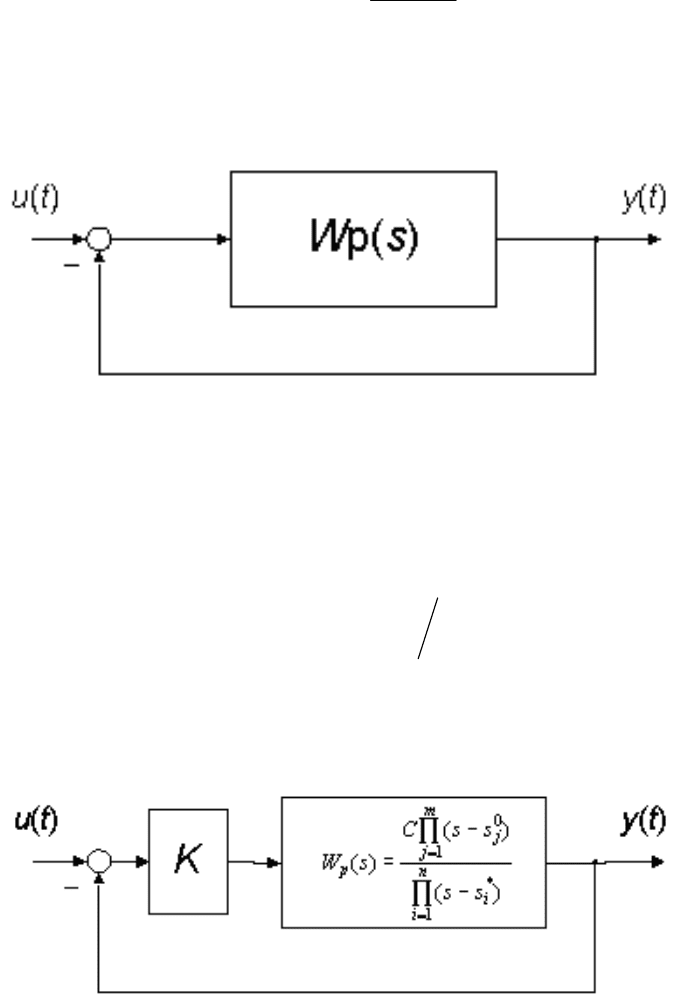
Структурная схема системы с обратной связью приведена на (рис. 9.1.).
Рис. 9.1
Структурная схема САУ
Из (9.1) следует, что нули передаточной функции замкнутой системы
равны нулям передаточной функции разомкнутой системы.
Задачу можно представить следующим эквивалентным образом. Есть
объект управления, определяемый передаточной функцией
0 *
1 1
( ) ( ) ( )
m n
j i
j i
W s C s s s s
= =
= − −
∏ ∏
(9.13)
Необходимо найти значение параметра пропорционального регулятора
(рис. 9.2.).
Рис. 9.2.
Эквивалентная схема САУ
Для определения полюсов замкнутой системы необходимо решить
уравнение:
W
p
(s) = – 1 (9.14)
Так как W
p
(s) является функцией комплексного переменного s, то
уравнение (14) распадается на два уравнения:
62
– уравнение модулей:
|W(s)|=1 (9.15)
– уравнение аргументов:
argW(s) = ± (2u +1)p , u =0, 1, 2, … (9.15 а)
для отрицательной обратной связи и
argW(s) = ± 2p , u =0, 1, 2, … (9.15 б)
для положительной обратной связи.
Уравнения (9.15) имеют наглядный геометрический смысл. Если точка s
является полюсом замкнутой системы, то, проведя в точку s вектора из всех
нулей W
p
(s) (обозначим аргументы этих векторов) и вектора из всех полюсов
W
p
(s) (обозначим аргументы этих векторов), уравнение (9.15 а) можно записать
в следующем виде:
( )
0 *
1 1
2 1
= =
θ − θ = ± + π
∑ ∑
n n
j i
j i
ν
, u = 0, 1, 2, … (9.16 a)
а уравнение (9.16 б) в виде:
0 *
1 1
2
= =
θ − θ = ± νπ
∑ ∑
n n
j i
j i
, u = 0, 1, 2, … (9.16, б)
Углы q отсчитываются от положительного направления действительной
оси. Знак угла “+” соответствует повороту против часовой стрелки, знак угла “–
” соответствует повороту по часовой стрелке.
Геометрическое место точек на комплексной плоскости “s”,
удовлетворяющее выражениям (9.16 а) и (9.16 б) называется корневым
годографом.
Как следует из (9.16), конфигурация корневого годографа не зависит от
коэффициента усиления K, но каждому конкретному значению K однозначно
соответствуют точки на корневом годографе.
Приведем свойства корневых годографов (случай отрицательной обратной
связи):
1.
Ветви корневого годографа непрерывны и расположены на комплексной
плоскости симметрично относительно действительной оси.

63
2.
Число ветвей КГ равно порядку системы n. Ветви начинаются в n
полюсах разомкнутой системы при K = 0. При возрастании K от 0 до
бесконечности полюса замкнутой системы двигаются по ветвям КГ.
3.
Отрезки действительной оси, по которым перемещаются действительные
полюса замкнутой системы, являются действительными ветвями корневого
годографа. Эти ветви находятся в тех частях действительной оси, справа от
которых расположено нечетное общее число действительных полюсов и нулей
разомкнутой системы.
4.
m ветвей КГ при возрастании K от 0 до бесконечности заканчиваются в m
нулях W
p
(s), a (n – m) ветвей при K, стремящемся к бесконечности, удаляются
от полюсов вдоль асимптот.
5.
Асимптоты в виде звезды из (n – m) полупрямых выходят из точки с
координатой
0 *
1 1= =
−
σ =
−
∑ ∑
m m
j i
j i
a
s s
n m
(9.17)
на действительной оси под углами
( )
2 1
, 0, 1
ν +
θ = π ν = − −
−
a
n m
n m
(9.18)
к действительной оси.
6.
Угол выхода
*
θ
i
ветви КГ из полюса
*
i
s
определяется из уравнения (9.16,
а), примененного к данному полюсу. Аналогично определяется угол входа
ветви КГ в нуль
0
j
s
.
7.
При расположении ветвей корневого годографа в левой полуплоскости s
САУ устойчива. При пересечении ветвей КГ мнимой оси слева направо САУ
становится неустойчивой. Пусть при K = K
кр
пересечение КГ с мнимой осью
произойдет в некоторой точке iw
кр
. Назовем это значение коэффициента
усиления критическим K
кр
, а величину w
кр
критической угловой частотой, на
которой система становится неустойчивой.
Метод КГ позволяет выбрать коэффициент усиления САУ, подобрать
расположение полюсов и нулей передаточной функции, корректирующих
звеньев, определить параметры доминирующих полюсов САУ (ближайших к
началу координат плоскости s).
В качестве примеров, приведем КГ для двух систем автоматического
управления.
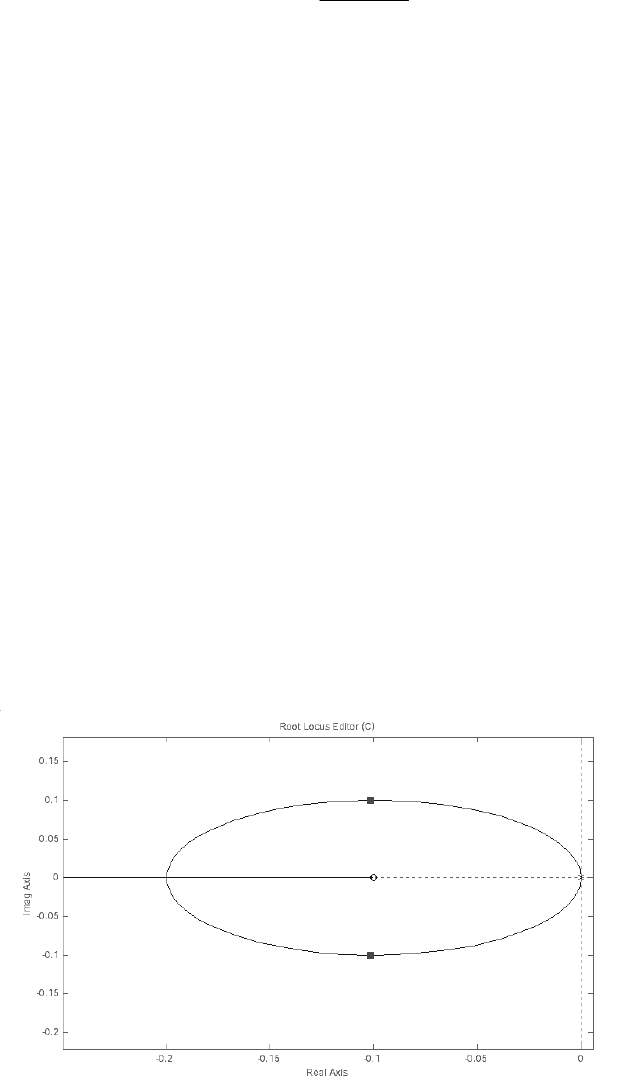
На рисунке рис. 9.3. приведен корневой годограф САУ, передаточная
функция разомкнутой системы, которой равна:
(
)
2
0.1
( )
K s
W s
s
⋅ +
=
(9.19)
64
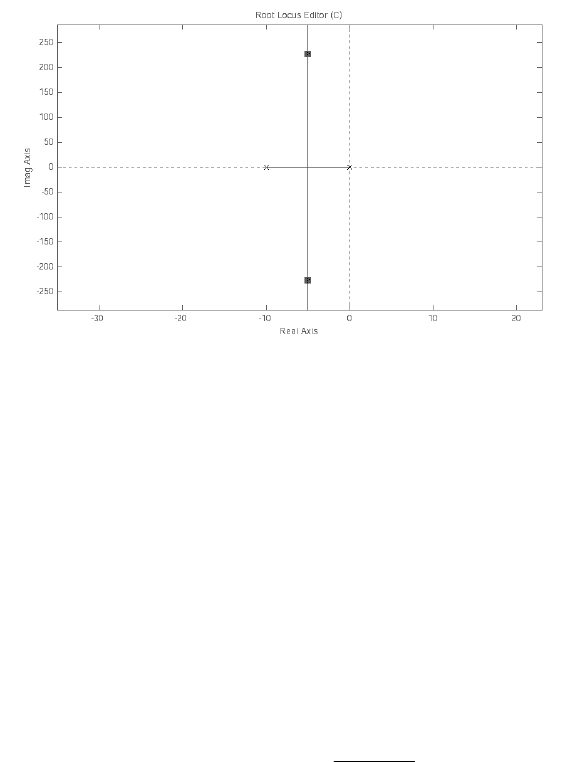
Рисунок 9.4. иллюстрирует КГ САУ с передаточной функцией разомкнутой
системы вида:
( )
( )
10
K
W s
s s
=
+
(9.20)
Последовательность выполнения
Для выполнения работы используется GUI-интерфейс “SISO-Design Tool”
из пакета прикладных программ Control System Toolbox.
Графический интерфейс предназначен для анализа и синтеза одномерных
линейных (линеаризованных) систем автоматического управления (SISO -
Single Input/Single Output).
В Control System Toolbox имеется тип данных, определяющих динамическую
систему в виде набора полюсов, нулей и коэффициента усиления передаточной
функции. Синтаксис команды, создающий LTI (Linear Time Invariant) ─ систему
в виде объекта ZPK (zero-pole-gain) c одним входом и одним выходом
(
)
0 0 * *
1 1
,... , ,... ,
m m
ZPK s s s s K
(9.21)
0 0
1
,...
m
s s
– значения нулей системы,
* *
1
,...
m
s s
– значения полюсов системы,
K – коэффициент усиления.
Рис. 9.3. Корневой годограф
65
Рис. 9.4. Корневой годограф
Более естественным является вариант, при котором с помощью функции
ZPK создается символьная переменная 's', которая затем используется для
определения передаточной функции. Например, после выполнения команд
s = zpk ('s'); W1 = (s+0.1)/(s^2) (9.22)
произойдет создание переменной W1 типа ZPK, определяющей передаточную
функцию вида
(
)
2
0.1
1
+
=
s
W
s
(9.23)
Запуск графического интерфейса SISO-Design Tool осуществляется
командой
Sisotool
или выбором соответствующего пункта в окне “Launch Pad”.
Для выполнения лабораторной работы необходимо выбрать в меню View
пункт Root Locus (корневой годограф), для отображения редактора Root Locus
Editor. В правом верхнем углу SISO-Design Tool можно менять тип обратной
связи (кнопка “+/–”) и структурную схему САУ.
Для загрузки данных из рабочего пространства MATLAB необходимо
использовать меню “File/Import”, в результате которой появляется диалог
Import System Data. Необходимо, чтобы в результате импортирования данных
получилась рассматриваемая схема САУ (рис. 9.1). Используя Root Locus Editor
и значение коэффициента усиления (здесь C – Current Compensator), выполнить
задания лабораторной работы. Изменение динамических и частотных
характеристик замкнутой системы при изменении K можно проследить
используя меню “Tools/Loop Responses”.
Таким образом, последовательность выполнения практической работы
следующая:

66
1.
Ознакомиться с основными элементами теории метода корневого
годографа.
2.
В соответствии с заданным вариантом нарисовать структурную схему
САУ.
3.
Запустить систему MATLAB.
4.
Создать zpk-объект, в соответствии с заданным вариантом.
5.
Определить значения полюсов и нулей разомкнутой системы W
p
(s).
6.
Запустить SISO-Design Tool и построить КГ.
7.
В соответствии с теорией проанализировать расположение ветвей
корневого годографа.
8.
Определить условия неустойчивости замкнутой САУ. Определить K
кр
и
w
кр
.
9.
Проанализировать влияние удаленных полюсов и нулей на величины K
кр
и w
кр
.
10.
Оформить отчет.
Методический пример
Пусть необходимо исследовать САУ с передаточной функция
разомкнутой системы:
( )
1
⋅
=
⋅ +
p
k e
W p
T p
τ
(9.24)
1.
Создадим ZPK-объект, найдем полюса и нули разомкнутой системы:
s= zpk('s'); W= (8400 *s^2 + 28 *s + 0.5)/(58800 *s^2 + 140*s )
Ноль/Полюс/Увеличение:
0.14286 (s^2 + 0.003333s + 5.952e-005)
---------------------------------------
s (s+0.002381)
>> pole(W)
ans =
0
-0.0024
>> zero(W)
67
ans =
-0.0017 + 0.0075i
-0.0017 - 0.0075i
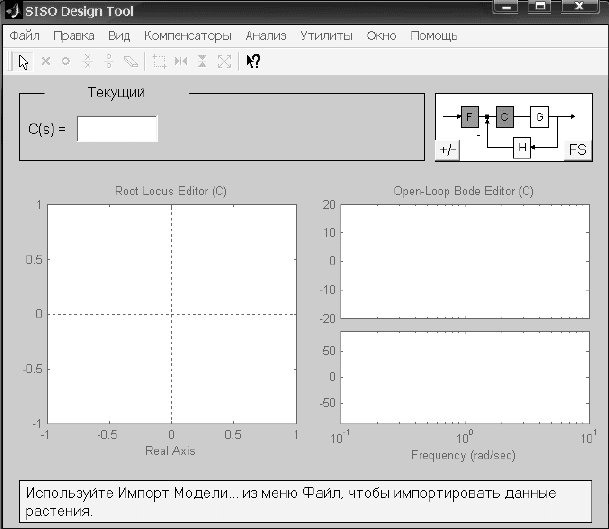
2.
Запустим SISO-Design Tool, настроим параметры и импортируем ZPK-
объект из рабочего пространства MATLAB (рис. 9.5.).
>> sisotool
Рис. 9.5. Окно siso-tools
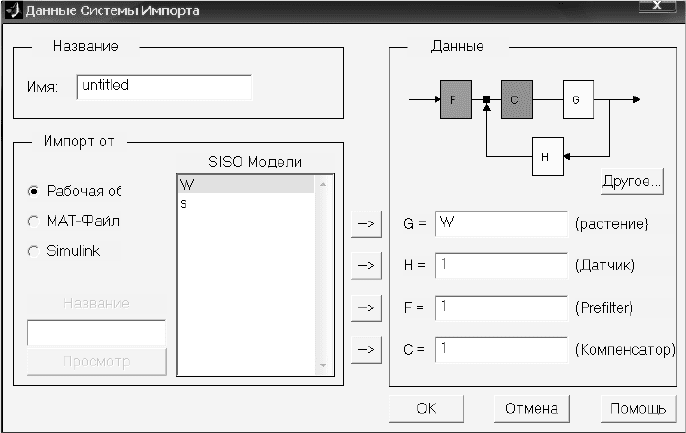
Далее экспортируем данные. Нажмем «Файл – Импорт – Добавим нашу
передаточную функцию – ОК » (рис 9.6.).
68
Рис. 9.6. Окно данные системы импорта
3.
Захватив “мышью”, передвигать красным курсором по корневому
годографу до пересечения ветвей с мнимой осью, определить значение K
к
р
.
Передвижение курсора происходит также при вводе значения коэффициента
усиления C в соответствующее поле ввода в верхней части GUI-интерфейса.
Для рассматриваемого случая K
кр
, значение w
кр
соответствует координате (0,
- j0).
4.
Для построения переходного процесса выбрать «Анализ-Другие ответы и
петли – нажать кнопку ОК».
Содержание отчета
1.
Построить корневой годограф.
2.
Получить коэффициент усиления K
кр
, при котором система находится на
границе устойчивости (если такой границы нет, то K
кр
принять равным 1).
3.
Нанести на ветви корневого годографа значения полюсов замкнутой
системы, соответствующие 0.5K
кр
, 0.25K
к
р
,K
к
р
,25K
к
р
,50K
к
р
.
4.
Построить для каждого значения K
к
р
графики переходного процесса,
частотной характеристики, амплитудно – фазовой характеристики, диаграммы
Никольса.
5.
Сделать выводы о зависимости.
6.
Привести выражение для W
з
(s) в виде произведения типовых звеньев.
Указать значения параметров типовых звеньев, написать название типовых
звеньев.
69
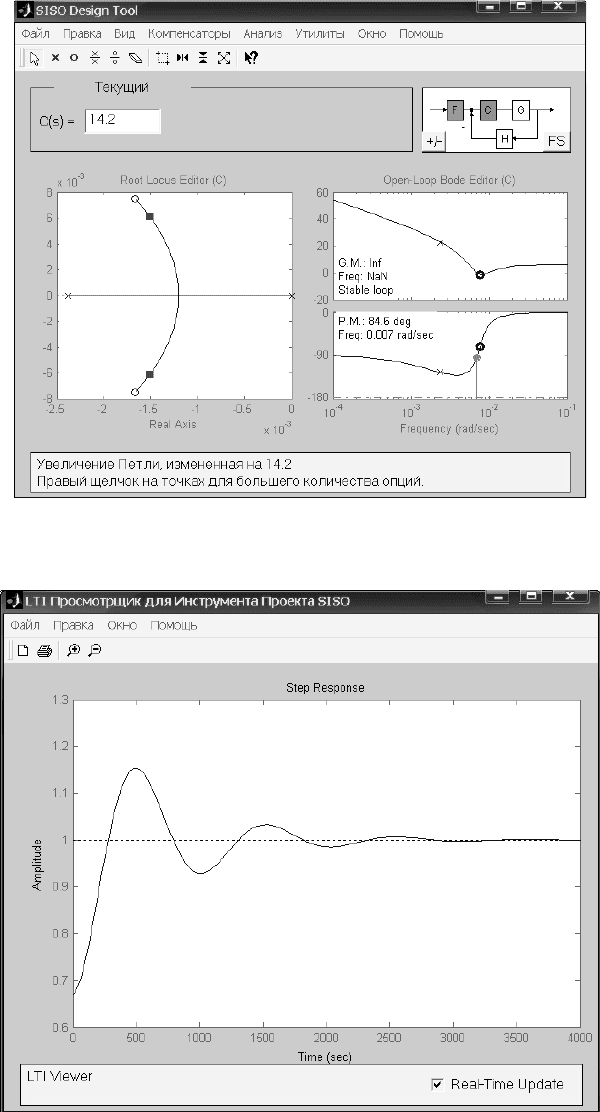
Рис. 9.7. Окно siso-tools
Рис. 9.8. Переходный процесс
Контрольные вопросы
1.
Как влияют полюса, нули на корневой годограф?
2.
Как влияет отрицательная обратная связь на устойчивость?
