Втюрин В.А. Автоматизированные системы управления технологическими процессами
Подождите немного. Документ загружается.


30
Задача 2
1. Был проанализирован график и получены табличные значения.
Таблица 5.2.
Анализируемые данные
Из графика видно, что функция достаточно гладкая, однако в области
t=200-300 имеется локальный максимум. Вполне возможно, что его появление
обусловлено недостоверностью исходных данных. Полученная зависимость, не
описывается какой - либо известной функцией. Предположим, что такой
функцией является полином n-ой степени. Выберем в качестве
интерполяционного полином второй степени:
2
bxbxaY ++=
.
Рис.5.3
.
Зависимость пропорционального множителя от температуры
2. Выберем в качестве аппроксимирующих следующие координаты
функции у(х) :
[ 50;1.0004 ], [ 100;1.0014 ], [ 300;1.0041 ]
Тогда система уравнений имеет вид:
T 0 50 100 150 200 250 300
K 1.0000
1.0004 1.0009 1.0014 1.0021 1.0026 1.0041

31
Решим эту систему, воспользовавшись матричными процедурами. В
Mathcad решение будет иметь вид:
Из решения получаем следующую функцию интерполяции:
y x( ) 1 3.6 10
6
−
⋅ x+ 3.2 10
8
−
⋅ x
2
⋅+:=
3.
В полученную функцию подставляем значения «
х
:=0…300», получаем
таблицу результатов для «
у(х)
», и строем график для этой функции аналогично
пункту 2. из первой задачи.
4.
Приведены графики исходной функции, представленной графически, и
функции интерполяции. Внешне они схоже друг другу (рис.5.4.).
5.
Для того, что бы определить погрешность интерполяции необходимо:
•
Создать векторы «
y
(
x
)» и «
К
».
•
Вычислить разность векторов
D=K-y
(
x
)
.
•
Находим скалярное произведение разности векторов
z=D·D
.
Вычисляем абсолютную среднеквадратическую погрешность
E
в режиме
калькулятора.
0 100 200 300
0.999
1
1.001
1.002
1.003
1.004
1.005
K
y x( )
t
x
,
Рис. 5.4.
Аналитические и теоретические графики
M
1
1
1
50
150
300
50
2
150
2
300
2
:=
B
1.0004
1.0014
1.0041
:=
M
1−
B⋅
1
3.6 10
6−
×
3.2 10
8−
×
=
32
Содержание отчета
1.
Выбрать табличные значения или из графика.
2.
Получить аналитическое выражение одним из методов интерполяции в
Mathcad.
Контрольные вопросы
1.
Из каких процедур складывается последовательность выполнения
интерполяции?
2.
Как определяется погрешность интерполяции?
Практическая работа № 6
ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОБЪЕКТА
УПРАВЛЕНИЯ.
Цель работы
– определить динамические характеристики объекта
управления.
y x( ) 1 3.6 10
6
−
⋅ x+ 3.2 10
8
−
⋅ x
2
⋅+:=
x
50
:=
y x( ) 1.00026
=
x
100
:=
y x( ) 1.00068
=
x
150
:=
y x( ) 1.00126
=
x
200
:=
y x( ) 1.002
=
x
250
:=
y x( ) 1.0029
=
x
300
:=
y x( ) 1.00396
=
K
1.0004
1.0009
1.0014
1.0021
1.0026
1.0041
:=
y x( )
1.0026
1.00068
1.00126
1.002
1.0029
1.00396
:=
D K y x(
)
−
:=
z D
D
⋅
:=
E
z
6
:=
E 3.737052 10
4
−
×=
33
Постановка задачи
Динамические характеристики снимались по каналу давления на линии,
которое регулировалось путём изменения хода регулирующего органа.
Измерения производили путём перемещения РО в процентном соотношении.
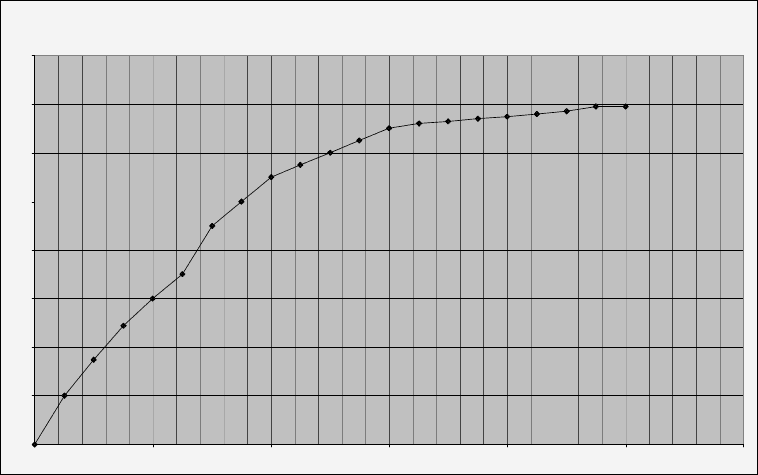
В результате эксперимента была получена кривая разгона, представленная на
(рис. 6.1.).
Последовательность выполнения
1.
Отображение анализируемых данных в графическом виде.
2.
Построение кривой для рассматриваемой зависимости.
3.
Анализ полученной кривой для рассматриваемой зависимости.
4.
Выводы о проделанной работе.
t=2,5
0
0,02
0,04
0,06
0,08
0,1
0,12
0,14
0,16
0 10 20 30 40 50 60
Рис. 6.1.
Экспериментальная кривая
Методический пример
По полученной кривой разгона методом площадей определяем
передаточную функцию линии прессования ДCтП.
Определяем передаточную функцию объекта, как произведение двух
передаточных функций W
з
(
p
)
= e
-τp
, соответствующей запаздыванию и W
y
(p),
соответствующей функции ∆
x
1
=
∆
x
вых
(
t-τ
), для которой за начало отсчёта
принято время
t=τ.

34
1.
Разбиваем отрезок времени от момента нанесения возмущения до
момента выхода величины φ(
x
вых
) на установившееся значение на отрезки
времени ∆
t
=2,5 сек., так чтобы на каждом участке кривая разгона мало
отличалась от прямой.
2.
В конце каждого интервала времени ∆
t
находим ∆
x
вых
и заносим их в
графу 2 таблицы 6.1.
Значение ∆
x
вых
в конце каждого интервала делим на ∆
x
вых
(∞) и получившееся
значение записываем в графу 3
С
4=
B
4/$
B
$24.
3.
Вычисляем 1- φ (
i
∆
t
) и заносим их в графу 4
D
4=1-
C
4.
4.
Подсчитываем сумму чисел графы 4, т. е. величину
[ ]
1
1 (
n
i
i t
=
− ϕ ∆
∑
D26=СУММА(D4:D24).
5.
Определяем площадь F1 по формуле:
[ ] [ ]
(
)
1
1 1 ( 0.5 1 (0)
F
n
i
t i tϕ ϕ
ϕ ϕϕ ϕ
ϕ ϕ
=
= ∆ ⋅ − ∆ − ⋅ −
∑
, минут (6.1)
А27=$A$5*($D$26-1*0.5).
6.
Изменяем масштаб времени
( )
Q( )
F1
i t
i t
∆
∆ = и заносим эти значения в
графу 5 E4=A4/$A$27.
7.
В графу 6, записываем значения
1 Q( )
i t
− ∆
, F4=1-E4.
8.
В графу 7, записываем значения
(
)
(
)
1 1 Q
− ϕ ⋅ −
G4=D4*F4.
9.
Подсчитываем сумму чисел графы 7, т.е. величину:
[ ]
( )
1
1 ( 1 Q
n
i
i t i t
=
− ϕ ∆ ⋅ − ∆
∑
(6.2)
G26=СУММ(G4:G24).
10.
Определяем площадь F2 по формуле:
( ) ( )
[ ]
2
1
F2 F1 Q 1 1 Q ) 1 (0)
=
= ∆ − ϕ ∆ ⋅ − ∆ − ∆ ⋅ − ϕ
∑
n
i
i t i t t
, мин (6.3)
B27=($A$27^2)*($G$26-2,5)*E5.
Все операции будут везде одинаковы, то можно воспользоваться
маркером заполнения.
11.
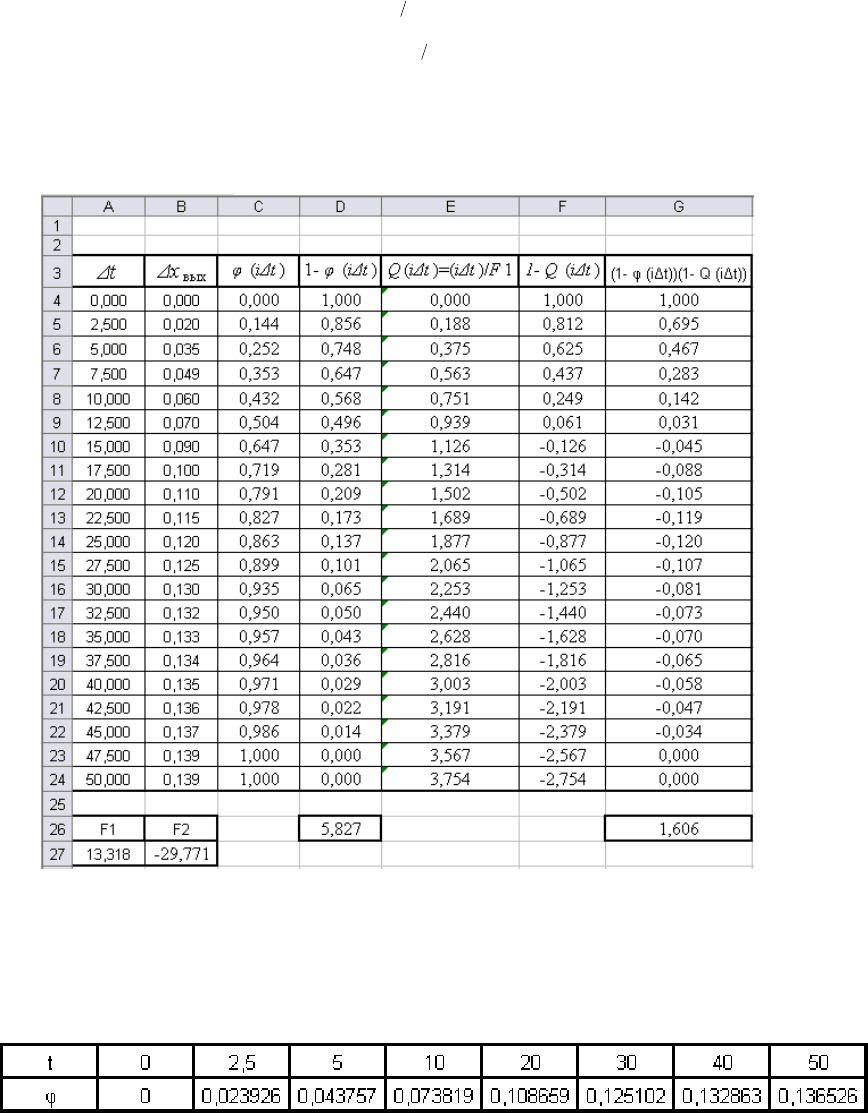
После всех вычислений (табл. 6.2) примет вид.
12.
Определяем вид передаточной функции. Если
∆x
вых
(0)=0, а
x
вых
не равно
0, то передаточная функция объекта в безразмерной форме имеет вид:

35
( )
2
1
1
2 1
1
W
1
+
=
+ +
b
p
a p a p
(6.4)
a1 = F1 =
11,443
a2 = F2 =
-71,36
В нашем случае F1 во много раз больше F2, следовательно,
коэффициентом F2 можно пренебречь и тогда передаточная функция будет
иметь следующий вид:
( )
1
1
1
W
1
=
+
p
a p
, (6.5)
где a
1
=F
1
=13,318 мин
Значит, передаточная функция имеет вид:
( )
1
W
13,318 1
=
⋅ +
p
p
(6.6)
Таким образом, передаточная функция в безразмерном виде исследуемого
объекта записывается в виде:
W(p) = Wз(p)* W(p) (6.7)
( )
0.139
W
13,318 1
−
=
⋅ +
pt
p e
p
(6.8)
Передаточную функцию в размерном виде можно представить так:
( )
(
)
( ) ( ) ( )
W
W W
∆Χ ∞
=
∆Υ ∞ ⋅ ⋅
ç ó
p
p p
(6.9)
( )
0.139
W
13,318 1
−
=
⋅ +
pt
p e
p
,
%
C
°
. (6.10)
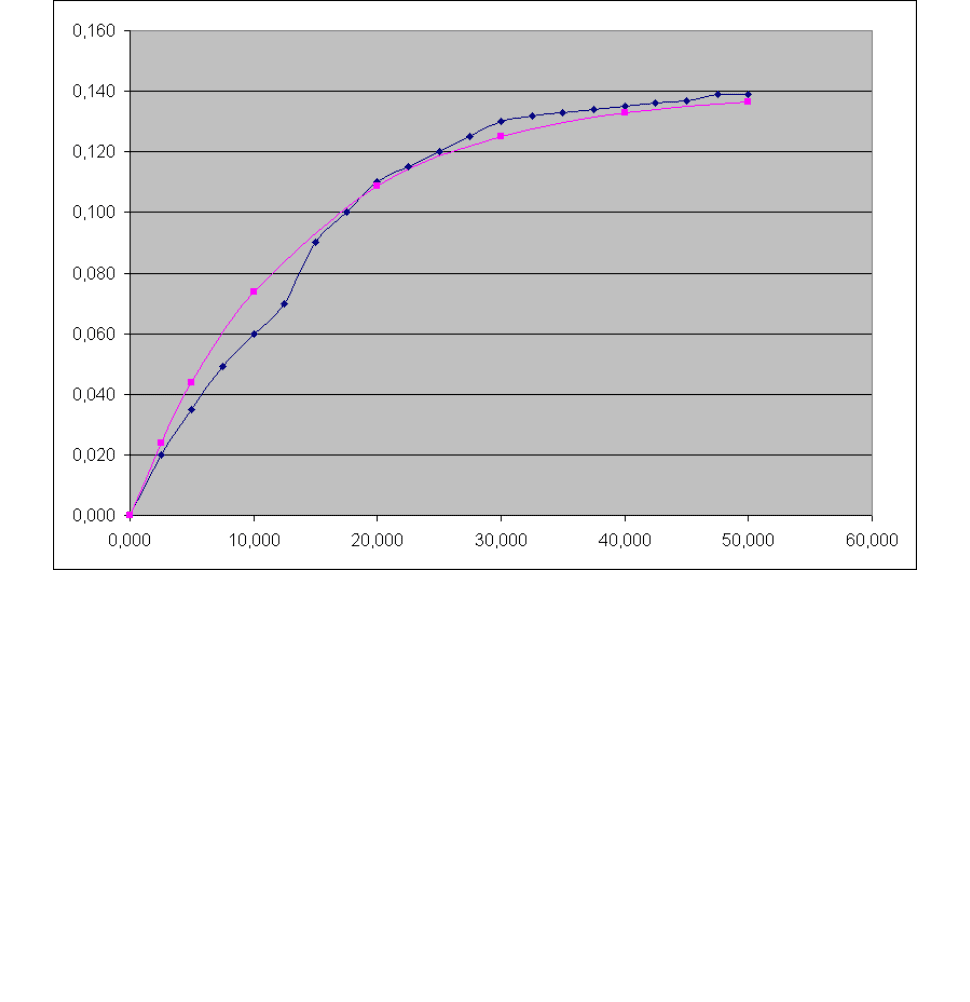
Для проверки построим теоретическую кривую разгона.
36
13,318
î á
13,318
(1 )
0.139 (1 )
−
−
ϕ = ⋅ −
ϕ = ⋅ −
t
t
K e
e
(6.11)
Таблица 6.2.
Определение передаточной функции.
Таблица 6.3.
Проверка теоретической кривой разгона.
37
Рис. 6.2.
Конечный график
Содержание отчета
1. Записать выбранные графические значения, взятые из приложения.
2. Получить передаточную функцию.
Контрольные вопросы
1.Что такое динамические характеристики объекта управления?
2. Как определяется правильность получения динамических характеристик?
Практическая работа № 7
ОПРЕДЕЛЕНИЕ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ
Корреляция
─ статистическая взаимосвязь двух или нескольких
случайных величин (либо величин, которые можно с некоторой допустимой
степенью точности считать таковыми). При этом изменения одной или
нескольких из этих величин приводят к систематическому изменению другой
или других величин. Мерой корреляции двух случайных величин служит
коэффициент корреляции.
38
Постановка задачи
Пусть дана таблица наблюдений некоторых значений (табл. 7.1.).
Таблица 7.1.
Значения наблюдений
№ Опыта Параметры
1 2 3 4 5 6 … n-1 n
Q Q
1
Q
2
Q
3
Q
4
Q
5
Q
5
Q
n-1
Q
n
ξ
1
ξ
11
ξ
12
ξ
13
ξ
14
ξ
15
ξ
16
ξ
n-1
ξ
n
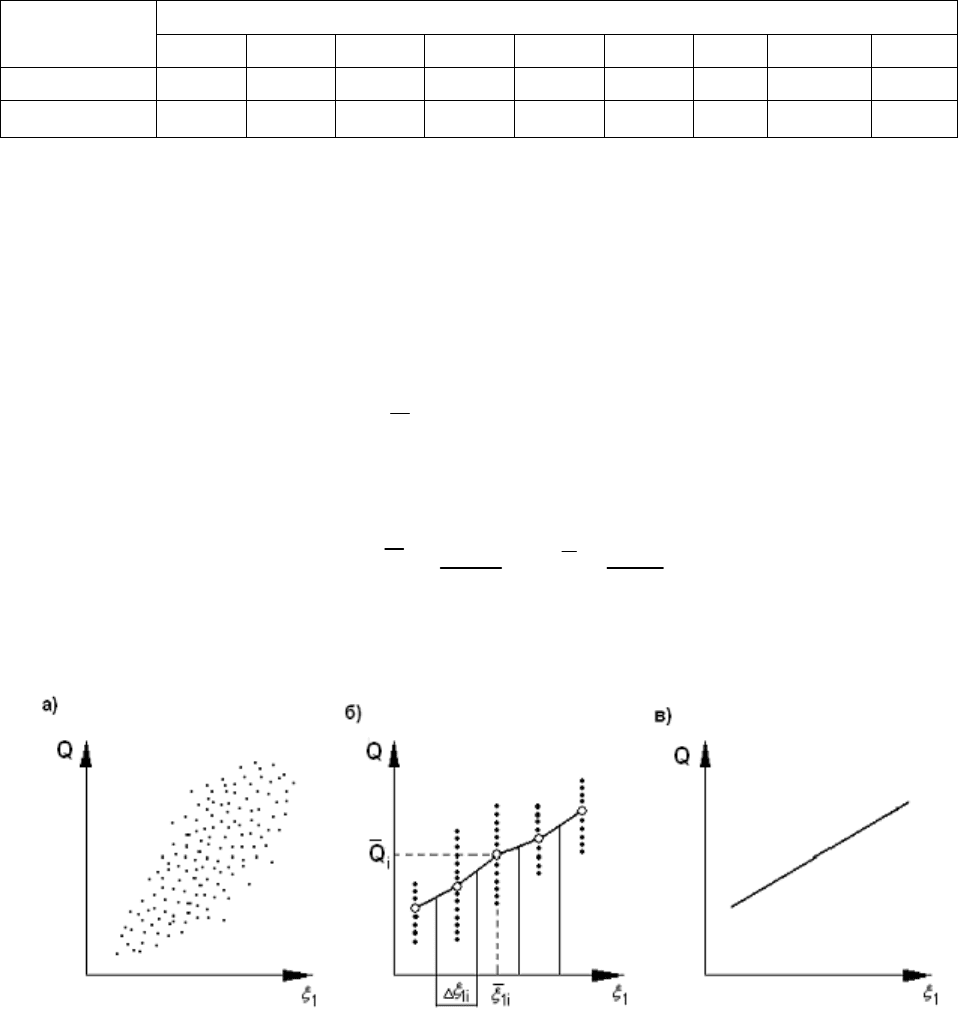
Перенесем данные таблицы 7.1 на координатную плоскость с осями Q и
ξ
1
.
Получим поле корреляции (рис.7.1,а). Каждому наблюдению из таблицы будет
соответствовать определенная точка на поле корреляции. Далее проследим
изменение статистических рядов распределения значений Q по значению
ξ
1
.
Для этого весь диапазон изменения
ξ
1
разобьем на ряд равных интервалов ∆
ξ
1
.
Все точки, попавшие в данный интервал ∆ξ
1i
, отнесем к его середине ξ
1i
.
Получим трансформированное поле корреляции (рис. 7.1, б).
Определим частные средние
i
Q
для каждого значения
ξ
i:
1=
=
∑
i
n
i
i
i
i
Q
Q
m
1
1
=
=
∑
i
n
i
i
i
m
ξ
ξ
(7.1)
где m
i
- число точек, оказавшихся в интервале.
Рис. 7.1.
Построение линии регрессии

39
Затем последовательно соединим точки Q
i
отрезками прямой. Полученная
ломаная линия называется эмпирической линией регрессии
Q по ξ
1
. Она
показывает, как с увеличением ξ
1
в среднем изменяется Q. Большим доверием
будут пользоваться те точки линии, которые принадлежат интервалам с
большим количеством наблюдений. С ростом числа наблюдений эмпирическая
линия регрессии будет освобождаться от случайных зигзагов, принимая все
более правильный, закономерный вид. Предельное положение эмпирической
линий регрессии, к которому она стремится при неограниченном увеличении
числа наблюдений, называется предельной теоретической линией регрессии
(рис. 7.1, в). Процесс нахождения линии регрессии заключается в выборе и
обосновании типа кривой и расчете параметров ее уравнения
Q = f (ξ
1
).
Для выбора и обоснования типа кривой регрессии существуют различные
пути: эмпирический, теоретический (опыт предыдущих исследований
логический анализ).
В данной работе поступим следующим образом, мысленно устраним те
зигзаги, которые предполагаем случайными на эмпирическом графике, и
определим порядок кривой регрессии.
В зависимости от сложности исследуемого объекта в качестве
аппроксимирующих уравнений могут быть выбраны различные классы
функций одного и многих переменных: степенные многочлены,
экспоненциальные и тригонометрические многочлены. В дальнейшем будем
рассматривать тип уравнения только для прямолинейной регрессии. Если
характер уравнения отличается от прямолинейного, необходимо подобрать его
тип.
Последовательность выполнения
1.
Отображение анализируемых данных в графическом виде.
2.
Построение кривой для рассматриваемой зависимости.
3.
Анализ полученной кривой для рассматриваемой зависимости.
4.
Выводы о проделанной работе.
Методический пример
1.
Создается таблица с данными от ячейки В2 до I2 последовательно в
строчку вводятся все точки попавшие в интервал
∆
ξ
= 8 (рис. 7.2.).
2.
Определим частные средние значение
i
Q
:
В ячейку В12 вводится функция для расчета среднего значения, она
имеет вид:
=СРЗНАЧ (B2:I2), на рисунке (рис. 7.3.) показан пример ввода. Эту
операцию нужно выполнять – вводя последовательно в каждый столбик
