Воеводин Вл. В. Численные методы, параллельные вычисления и информационные технологии
Подождите немного. Документ загружается.


ICA PCA
M
(w
∗
z(t)),
T
T.
Φ
(k)
y
:= E[y(t)y
∗
(t)]
[0:kT ]
,
Φ
(k+1)
y
Φ
(k+1)
y
:=
k
k+1
Φ
(k)
y
+
1
k+1
E[y(t)y
∗
(t)]
[kT :kT +T ]
=
=
k
k+1
Φ
(k)
y
+
1
k+1
E[y
[k+1]
(t)y
[k+1]
(t)
∗
].
PCA
Ψ
y
= E[G(y)]
1. y
[1]
. Ψ
(1)
y
.
k. y
[k]
. E[G(y
[
k])]
Ψ
(k)
y
Ψ
(k)
y
= α
k
Ψ
(k−1)
y
+ (1 − α
k
)E[G(y
[
k])].
α
k

α
k
= 0
α
k
=
k−1
k
Ψ
(k)
[0 : kT ].
k
α
k
= 1
T
α
k
α
k
,
α
k
α
k
.

α
k
,
α
k
= (k − 1)/k
α
k
= 0
y
[k]
, k = 1, . . . , N.
x
[k]
Ψ
y
= E[G
p
(y)], p = 1, . . . , n
p
,
α
k
.
k
y
[k]
.
E[G
p
(y
[
k])]
α
k
.
Ψ
(k)
y
. W
(k−1)

x
[k]
= W
(k)
y
(k)
.
x
[k]
x
[k−1]
.
W
[k−1]
A
[k]
= P
k
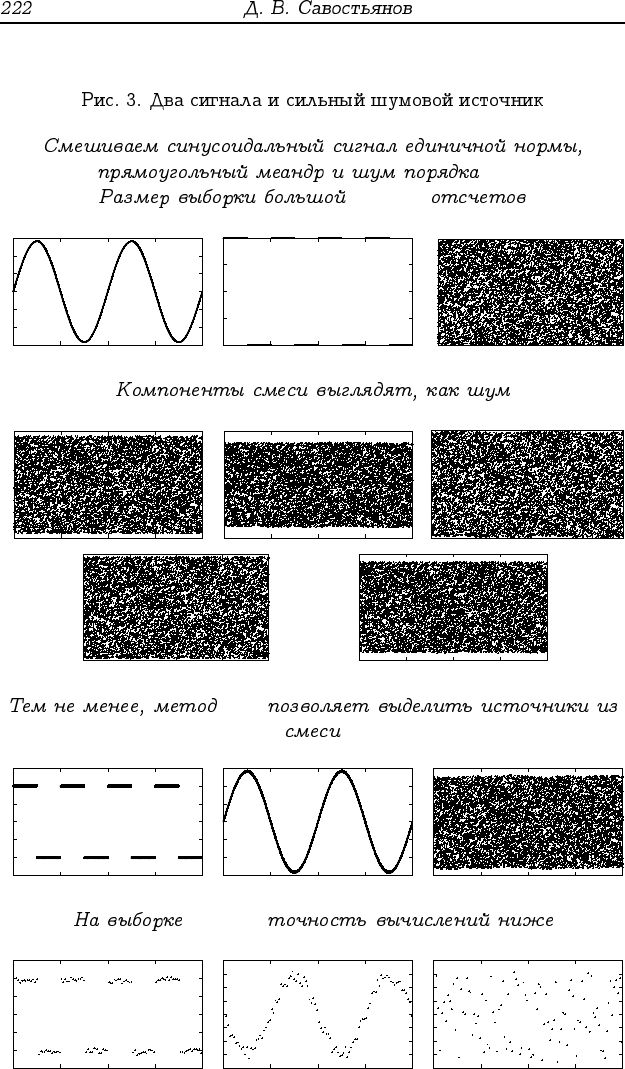
10
3
.
l = 10
4
x
1
(t)
4π3π2π1π0π
1.5
1
0.5
0
-0.5
-1
-1.5
x
2
(t)
4π3π2π1π0π
1
0.5
0
-0.5
-1
x
3
(t)
4π3π2π1π0π
1000
800
600
400
200
0
-200
-400
-600
-800
-1000
y
1
(t)
4π3π2π1π0π
600
400
200
0
-200
-400
-600
y
2
(t)
4π3π2π1π0π
150
100
50
0
-50
-100
-150
y
3
(t)
4π3π2π1π0π
50
40
30
20
10
0
-10
-20
-30
-40
-50
y
4
(t)
4π3π2π1π0π
1000
800
600
400
200
0
-200
-400
-600
-800
-1000
y
5
(t)
4π3π2π1π0π
300
200
100
0
-100
-200
-300
BSS
bss
1
(t)
4π3π2π1π0π
1.5
1
0.5
0
-0.5
-1
-1.5
bss
2
(t)
4π3π2π1π0π
1.5
1
0.5
0
-0.5
-1
-1.5
bss
3
(t)
4π3π2π1π0π
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
l = 100
bss
1
(t)
4π3π2π1π0π
1.5
1
0.5
0
-0.5
-1
-1.5
bss
2
(t)
4π3π2π1π0π
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
bss
3
(t)
4π3π2π1π0π
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
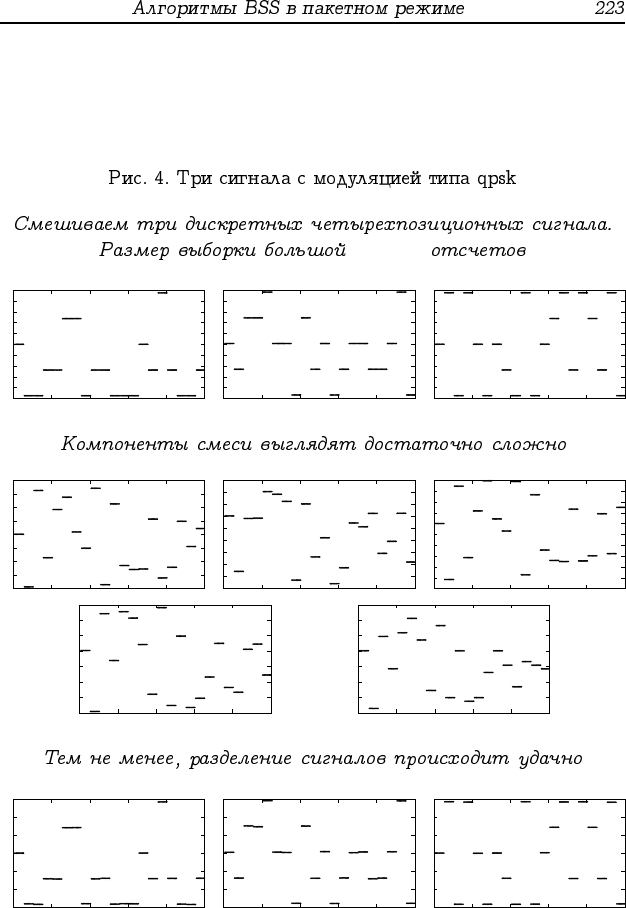
l = 10
4
x
1
(t)
10.80.60.40.20
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
x
2
(t)
10.80.60.40.20
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
x
3
(t)
10.80.60.40.20
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
y
1
(t)
10.80.60.40.20
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
y
2
(t)
10.80.60.40.20
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
-1.2
y
3
(t)
10.80.60.40.20
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
-1.2
y
4
(t)
10.80.60.40.20
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
y
5
(t)
10.80.60.40.20
1.5
1
0.5
0
-0.5
-1
-1.5
-2
bss
2
(t)
10.80.60.40.20
1.5
1
0.5
0
-0.5
-1
-1.5
bss
3
(t)
10.80.60.40.20
1.5
1
0.5
0
-0.5
-1
-1.5
bss
1
(t)
10.80.60.40.20
1.5
1
0.5
0
-0.5
-1
-1.5

BSS
BSS
//
//
//

//
//
//
//
//
//
//
// 6
//

//
//
//
//
//
//
//
//
//
//

//
//
// 4
//
//
//
//
//
