Воеводин Вл. В. Численные методы, параллельные вычисления и информационные технологии
Подождите немного. Документ загружается.


M
(w
∗
z) = E[G(|w
∗
z|
2
)]
E[|w
∗
z|
2
] = kwk
2
= 1.
∇E[G(|w
∗
z|
2
)] − β∇E[|w
∗
z|
2
] = 0.
w.
∇E[G(|ξ|
2
)] =
∂
∂w
1r
∂
∂w
1i
∂
∂w
nr
∂
∂w
ni
E[G(|w
∗
z|
2
)] = 2
E[ℜ(z
1
ξ
∗
)g(|ξ|
2
)
E[ℑ(z
1
ξ
∗
)g(|ξ|
2
)
E[ℜ(z
n
ξ
∗
)g(|ξ|
2
)
E[ℑ(z
n
ξ
∗
)g(|ξ|
2
)
,
ξ = w
∗
z.
∇E[|w
∗
z|
2
] = 2
ℜ (w
1
)
ℑ(w
1
)
ℜ (w
n
)
ℑ(w
n
)
E[zz
∗
] = I.
∇E
G(|w
∗
z|
2
)
∇
2
E
G(|w
∗
z|
2
)
= 2E
(∇
2
|w
∗
z|
2
)g(|w
∗
z|
2
)+
+ 2(∇|w
∗
z|
2
)(∇|w
∗
z|
2
)
⊤
g
′
(|w
∗
z|
2
)
≈
≈ 2E
g(|w
∗
z|
2
) + |w
∗
z|
2
g
′
(|w
∗
z|
2
)
I,
g = G
′
,
E[zz
⊤
] =
0,
β∇
2
E[|w
∗
z|
2
] = 2βI.

J = 2(E
g(|w
∗
z|
2
) + |w
∗
z|
2
g
′
(|w
∗
z|
2
)
− β)I.
w
+
= w −
E
z(w
∗
z)
∗
g(|w
∗
z|
2
)
− βw
E [g(|w
∗
z|
2
) + |w
∗
z|
2
g
′
(|w
∗
z|
2
)] − β
w
= w
+
/kw
+
k.
w
+
= E[z(w
∗
z)
∗
g(|w
∗
z|
2
)] − E[g(|w
∗
z|
2
) + |w
∗
z|
2
g
′
(|w
∗
z|
2
)]w;
w = w
+
/kw
+
k.
ICA
w
{0}
k = 0.
w := E[z(w
∗
z)
∗
g(|w
∗
z|
2
)] − E[g(|w
∗
z|
2
) + |w
∗
z|
2
g
′
(|w
∗
z|
2
)]w;
w
w w
w = w

w
W.
x(t)
x(t) = w
∗
z(t).
W.
w
W.
W
w
:= (I − WW
∗
) w .
w
W
x(t) = W
∗
z(t),
z(t)
ICA PCA
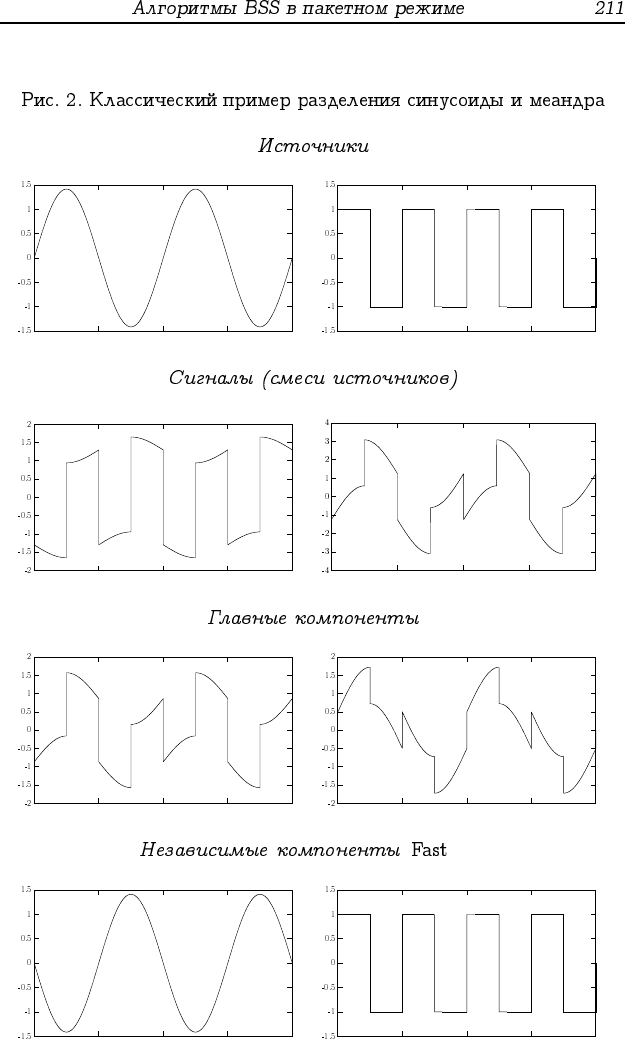
x
1
(t)
4π3π2π1π0π
x
2
(t)
4π3π2π1π0π
y
1
(t)
4π3π2π1π0π
y
2
(t)
4π3π2π1π0π
z
1
(t)
4π3π2π1π0π
z
2
(t)
4π3π2π1π0π
ICA
s
1
(t)
4π3π2π1π0π
s
2
(t)
4π3π2π1π0π

Φ
y
Q
y
,
A
Φ
y
= AD
Φ
A
∗
, Q
y
= AD
Q
A
∗
Φ Q
(∗).
p
A
k
= UΛ
k
V
⊤
,
kA
k
− UΛ
k
V
⊤
k →
U, V Λ
k
.

a
k
ij
=
X
α
u
iα
λ
kα
v
jα
,
A = [a
ijk
]
a
ijk
=
X
α
u
ia
v
ja
w
ka
,
W
Λ
k
.
Q
Q
y
(t) = E
(t:t+∆t)
[y(t)y
∗
(t)] = AE
(t:t+∆t)
[x(t)x
∗
(t)]A
∗
= AQ
x
(t)A
∗
.
Q
y
= Q
y
(t) t,
Q
y
Q
y
(t)
t,
Φ
y
,
Q
k
y
= Q
y
(t
k
)
t
k
Q
k
y
.
Q
y
(τ) = E[y(t)y
∗
(t + τ)] = AE[y(t)y
∗
(t + τ)]A
∗
= AQ
x
(τ)A
∗
.
τ.

t τ
(C
y
)
ijkl
= E[y
i
y
j
y
k
y
l
]−E[y
i
y
j
]E[y
k
y
l
]−E[y
i
y
k
]E[y
j
y
l
]−E[y
i
y
l
]E[y
j
y
k
].
Φ
y
C
y
,
y(t),
)
Φ
y
= AΦ
x
A
∗
, C
y
= C
x
×
1
A ×
2
A ×
3
A ×
4
A.
Φ
x
C
x
,
i = j = k = l,
A.
A =
B,D
C
y
− D ×
1
B ×
2
B ×
3
B ×
4
Bk (diag)
n m
)
×
p
p
A = [a
ijkl
] n× n× n× n B
m×n ×
2
C = [c
ijkl
]
n × m × n × n,
c
ijkl
=
n
X
j
′
=1
a
ij
′
kl
b
jj
′ .

m > n.
C
z
m × m × m × m, m
2
C = [(c
ij
)
α
] = (C
z
)
ij(kl)
, (kl) ↔α.
C
m
2
C
α
.
(diag)
A =
B,Q,D
C − D ×
1
B ×
2
B ×
3
Qk (diag
′
)
A,
Q
B.
BSS
T
N T
T

T .
(∗).
T ,
T,
A
N T,
T = NT.
W

ICA
ICA
W,
M
(w
∗
z(t)).
T y
[1]
(t),
z
[1]
(t)
ICA
W
(1)
. y
[2]
y
[1]
(t) z
[1]
(t)
M
(w
∗
z(t)) =
M
(w
∗
z
[1]
(t)) +
M
(w
∗
z
[2]
(t)),
w.
W
(2)
ICA
ICA
A
