Воеводин Вл. В. Численные методы, параллельные вычисления и информационные технологии
Подождите немного. Документ загружается.


//
//
//


σ
∂ϕ(M)
∂n
M
= −
∂ϕ
0
(M)
∂n
M
, M ∈ σ
∆ϕ(M) + κ
2
ϕ(M) = 0, M ∈ D,
κ =
2πν
c
ν
~
n
M
σ,
D. D
σ
ψ = ψ(u, v), (u, v) ∈ R
2
, ψ ∈ C
1
.
ϕ
0
(M)
ϕ
0
(M) =
m
X
i=1
Q
i
4π
(iκr
MM
i
)
r
MM
i
, M
i
∈ D, i = 1, . . . , m
Q
i
M
i
D.
D
~
r
M
r
M
, ∇ϕ(M)
− iκϕ(M) = O
1
R
MM
0
,

R
MM
0
M M
0
∈ σ,
r
M
= |
~
r
M
| = |x
M
~
i+ +y
M
~
j + z
M
~
k| =
q
x
2
M
+ y
2
M
+ z
2
M
,
~
i,
~
j,
~
k
σ
ϕ(M) =
Z
σ
g(N)G(M, N)dσ
N
, M ∈ D, M 6∈ σ,
g(N), N ∈ σ
G(M, N) =
1
4π
∂
∂n
N
(iκr
MN
)
r
MN
.
g(M) M ∈ σ
Z
σ
g(N)
∂G(M, N)
∂n
M
dσ
N
= −
∂ϕ
0
(M)
∂n
M
, M ∈ σ.
σ
z = 0,
g(N) = 2ϕ
0
(N), N ∈ σ.
κ.
κ ∼ 0,1 . . . 10.

σ
σ u, v.
σ
ij
, i, j = 1 . . . n g(N)
Ag = b.
A
a
ij
(M) = −
Z
L
σ
ij
~
n
M
·
−→
dl × ∇
N
F(M, N)
+
+k
2
Z
σ
ij
F(M, N)
~
n
M
·
~
n
N
dσ, i, j = 1 . . . n,
L
σ
ij
σ
ij
,
F(M, N) =
1
4π
(iκr
MN
)
r
MN
.
g(N) κ
κ
A n > 2·10
4
A
ε
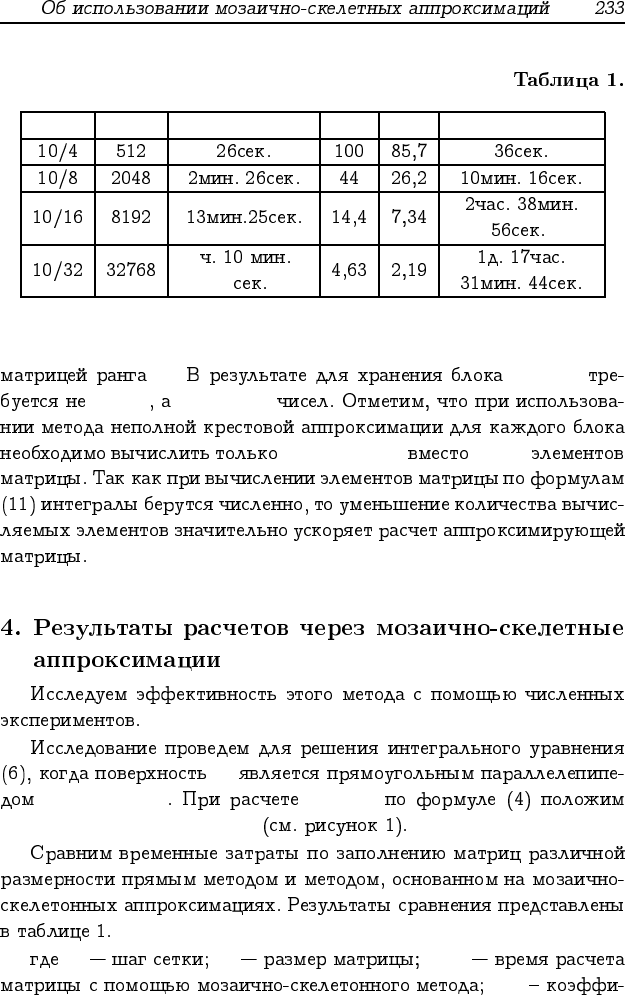
h n T
ms
I
re
I
im
T
st
1
27
k. l
1
× l
2
l
1
· l
2
k(l
1
+ l
2
)
O(k(l
1
+ l
2
)) l
1
·l
2
σ
20 × 30 × 40 ϕ
0
(M)
m = 1; Q
1
= 1; M
1
(20; 0; 0)
h n T
ms
I
re
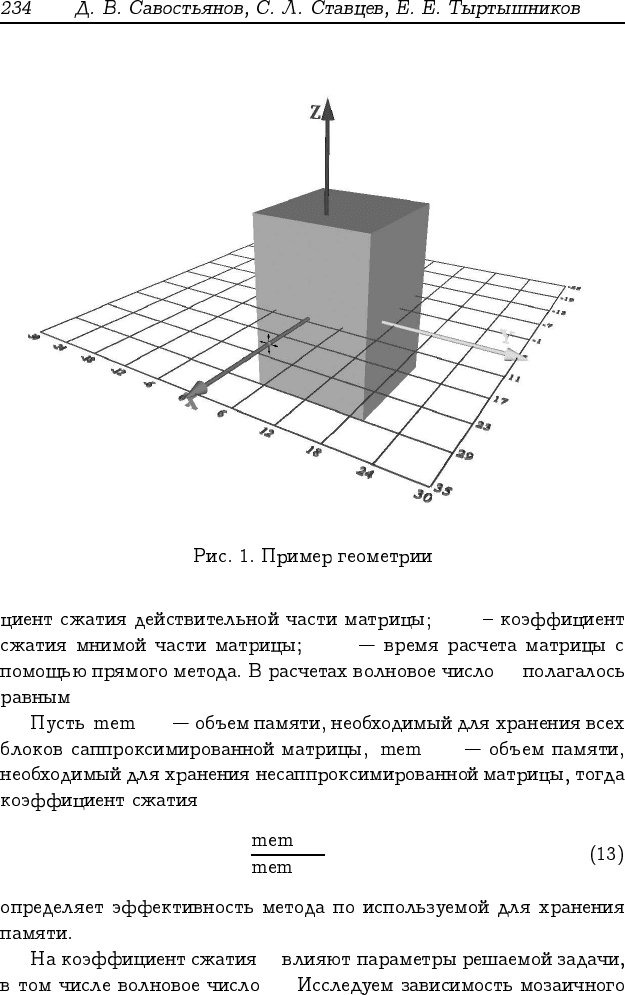
I
im
T
ms
κ
0,2.
(A)
(A)
I =
(A)
(A)
·100
I
κ.

R =
2nI
100
κ
n = 8192.
iκr/r
< (κa −
2
ε)
α
2
n, α = 2,
a
ε
ε = 10
−4
R(κ)
α.
α =
< xy > − < x >< y >
< x
2
> −(< x >)
2
,
x = (κa −
2
ε), y = (R), < · >
α
Re
≈ 0,69, α
Im
≈ 1,32.
α
κ
g
κ
κ
R
Re
R
Im
κ
R
Re
R
Im

λ 2π
T
κ
d
OZ
OXZ
σ x = 10 d = 5 , d = 1 d = 0, 5 .
d
g N
∗
∈ σ
g(N)
N
∗
.
h(N) = g(N) − p
Q
(N), N ∈ σ,
κ
h
n
I
Re
I
Im
T
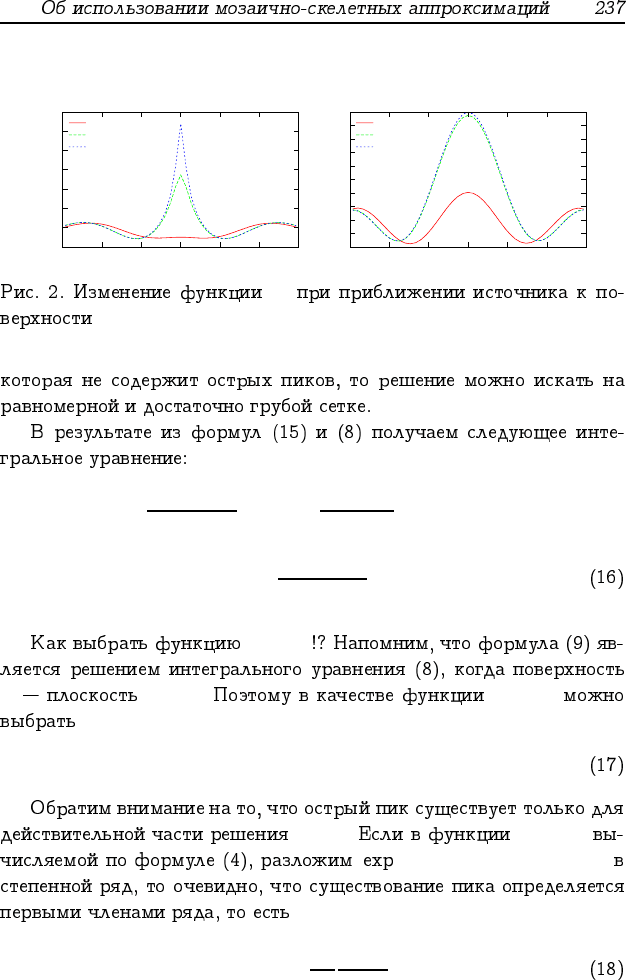
d = 0.5
d = 1
d = 5
Re(g)
151050
−5−10−15
0.3
0.25
0.2
0.15
0.1
0.05
0
−0.05
d = 0.5
d = 1
d = 5
Im(g)
151050
−5−10−15
0.08
0.07
0.06
0.05
0.04
0.03
0.02
0.01
0
−0.01
−0.02
g
Z
σ
h(N)
∂G(M, N)
∂n
M
dσ
N
= −
∂ϕ
0
(M)
∂n
M
−
−
Z
σ
p
Q
(N)
∂G(M, N)
∂n
M
dσ
N
, M ∈ σ.
p
Q
(N)
σ z = 0. p
Q
(N)
p
Q
(N) = 2ϕ
0
(N), N ∈ σ.
g(N). ϕ
0
(N),
(iκr
NM
i
), i = 1, . . . , m
ϕ
R
(N) =
m
X
i=1
Q
i
4π
1
r
NM
i
,
