Виноградов А.Б. Векторное управление электроприводами переменного тока

31

Для частного случая симметричных процессов удобнее пользо-

ваться следующей формой записи уравнений:

;)(0

;

rk

r

rr

sk

s

sss

j

dt

d

IR

j

dt

d

IRU

Ψ−+

Ψ

+=

Ψ+

Ψ

+=

r

rr

ωω

ω

;

smrrr

rmsss

ILIL

rrr

r

+=Ψ

;

2

3

sr

r

m

p

I

L

ZM

r

×Ψ=

.

c

MM

dt

d

Z

J

p

−=

ω

(3.9)

Дифференциальные уравнения электромагнитных процессов

обычно упрощают, записывая их относительно каких-либо двух век-

торных переменных состояния, исключая остальные с помощью урав-

нений связи. Рассмотрим несколько вариантов более удобной записи

уравнений.

3.3. Запись уравнений относительно потокосцеплений статора

и ротора

Из уравнений связи (третье и четвертое уравнения системы (3.9))

выразим векторы

токов статора и ротора, подставим их в первое, вто-

рое и пятое уравнения системы (3.9).

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

Ψ

r

s

rm

ms

r

s

I

LL

r

;

2

)(

mrs

rmsr

rm

ms

rr

ms

s

LLL

LL

L

I

−

Ψ−Ψ

=

Ψ

=

rr

r

;

2

)(

mrs

smrs

rm

ms

rm

ss

r

LLL

LL

L

I

−

Ψ−Ψ

=

Ψ

=

rr

r

;

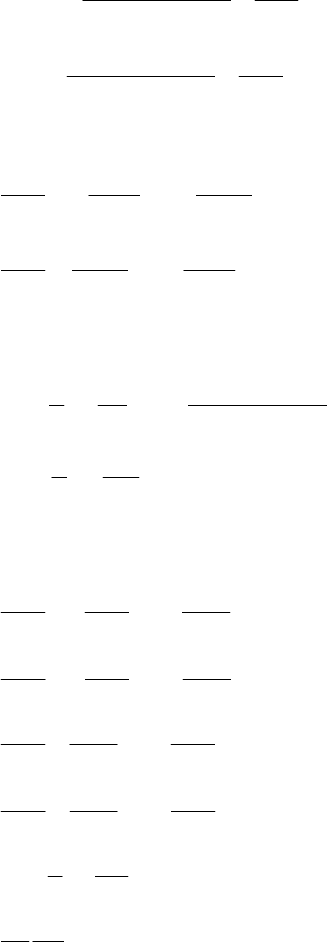
32

rk

r

mrs

smrs

r

sk

s

mrs

rmsr

ss

j

dt

d

LLL

LL

R

j

dt

d

LLL

LL

RU

Ψ−+

Ψ

+

−

Ψ−Ψ

=

Ψ+

Ψ

+

−

Ψ−Ψ

=

r

rr

r

)(

0

;

)(

2

ωω

ω

или в форме Коши

,)(

;

rkr

m

sr

s

m

mr

r

sksr

m

ms

s

m

rss

j

K

LR

K

LR

dt

d

jU

K

LR

K

LR

dt

d

Ψω−ω−Ψ−Ψ=

Ψ

Ψω−+Ψ+Ψ−=

Ψ

rrr

r

rrrr

r

(3.10)

где

.

2

mrsm

LLLK −=

Уравнение электромагнитного момента запишется как

;

)(

2

3

2

⎟

⎠

⎞

⎜

⎝

⎛

−

Ψ−Ψ

×Ψ=

mrs

rmsr

r

m

p

LLL

LL

L

ZM

r

sr

m

p

K

L

ZM Ψ×Ψ=

rr

2

3

.

(3.11)

Уравнение движения остается без изменений.

Переходя к проекциям в системе координат (

x,y), получим

;)(

;

rxkry

m

sr

sy

m

mr

ry

rykrx

m

sr

sx

m

mrrx

sxkyry

m

ms

sy

m

rs

sy

sykxrx

m

ms

sx

m

rssx

K

LR

K

LR

dt

d

K

LR

K

LR

dt

d

U

K

LR

K

LR

dt

d

U

K

LR

K

LR

dt

d

Ψ−−Ψ−Ψ=

Ψ

Ψ−+Ψ−Ψ=

Ψ

Ψ−+Ψ+Ψ−=

Ψ

Ψ++Ψ+Ψ−=

Ψ

ωω

ω

;)(

2

3

sxrysyrx

m

p

K

L

ZM ΨΨ−ΨΨ=

.

c

MM

dt

d

Z

J

p

−=

ω

(3.12)

Система уравнений (3.12) представляет собой математическую

модель АД, записанную в ортогональной системе координат (

x,y), от-

носительно потокосцеплений статора и ротора. Она довольно удобна

для вычислений на ЭВМ. Все остальные переменные машины: токи

статора, ротора, намагничивания, потокосцепление намагничивания

—

рассчитываются на основе алгебраических уравнений связи этих пере-

менных с потокосцеплениями статора и ротора.

33

;)(

1

;)(

1

rymsyr

m

syrxmsxr

m

sx

LL

K

ILL

K

I Ψ−Ψ=Ψ−Ψ=

;)(

1

;)(

1

symrys

m

rysxmrxs

m

rx

LL

K

ILL

K

I Ψ−Ψ=Ψ−Ψ=

.;;)(;)(

mymmymxmmxrysymyrxsxmx

ILILIIIIII

=

Ψ

=

Ψ

+

=

+=

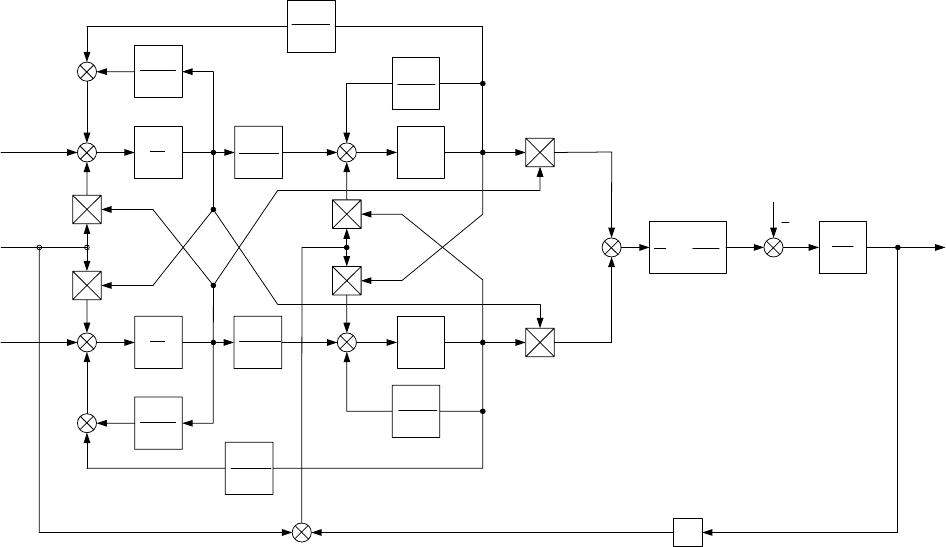
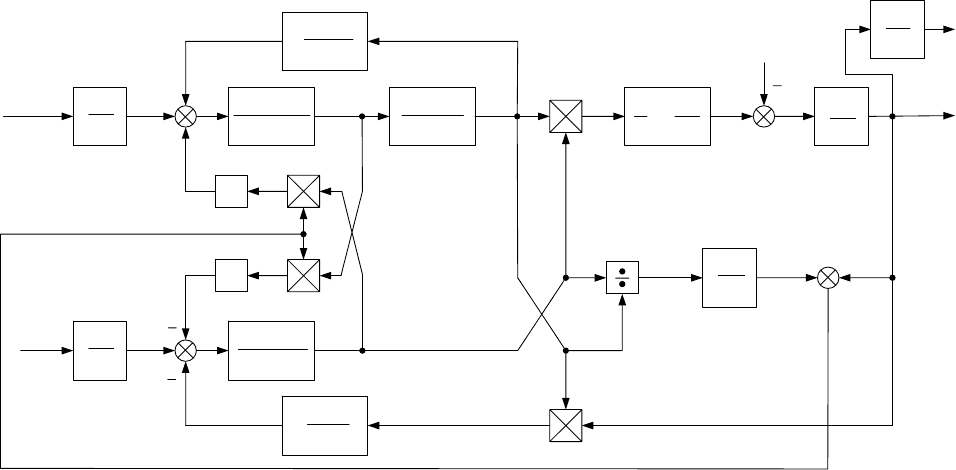
Структурная схема асинхронного двигателя, построенная по урав-

нениям (3.12), изображена на рис.3.5.

3.4. Запись уравнений относительно тока статора

и потокосцепления ротора

Из уравнений связи исходной системы уравнений (3.9) выразим

ток ротора и потокосцепление статора и подставим их в остальные

уравнения.

,1(

)(;)(

1

2

r

m

r

m

s

rs

m

s

smr

r

m

sssmr

r

L

I

LL

L

IL

L

LIL

L

I

Ψ+=Ψ+−=

=−Ψ=Ψ−Ψ=

rrr

rrrrrr

)

ss

s

IL

I +

r

σ

где

rs

m

LL

L

2

1−=

σ

— коэффициент рассеяния.

rk

r

smr

r

m

ssk

r

ms

ssss

j

dt

d

IL

L

R

L

ILj

dt

d

L

dt

Id

LIRU

Ψ−+

Ψ

+−Ψ=

Ψ++

Ψ

++=

r

rr

r

rr

)()(0

;)(

ωω

σωσ

или

m

ms

K

LR

∫

p

1

p

1

m

mr

K

LR

m

rs

K

LR

m

mr

K

LR

m

rs

K

LR

m

ms

K

LR

m

sr

K

LR

m

sr

K

LR

∫

m

p

K

L

Z

2

3

Jp

1

M

c

M

p

Z

r

ω

y

U

x

U

sx

Ψ

ry

Ψ

sy

Ψ

k

ω

rx

Ψ

Рис.3.5. Структурная схема АД в ортогональных осях (x,y)

34

.)(

;

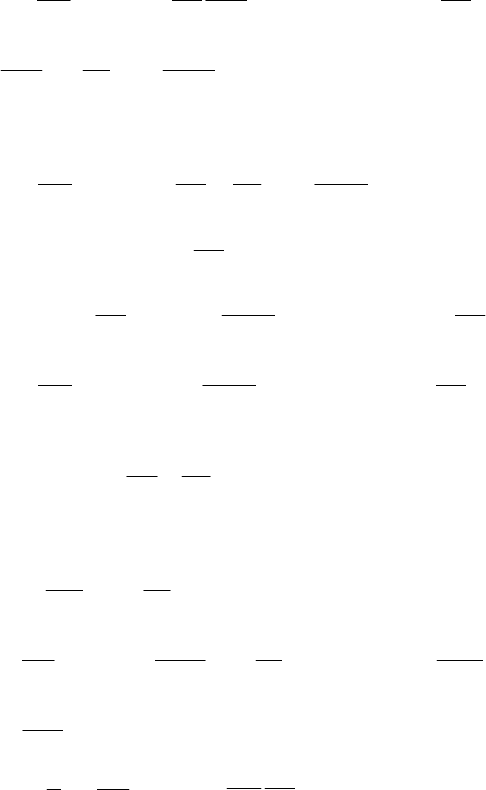
rks

r

rm

r

rr

rk

r

m

skss

r

m

ss

s

jI

L

RL

L

R

dt

d

L

jILjU

dt

d

L

IR

dt

Id

L

Ψ−−+Ψ−=

Ψ

Ψ−−+

Ψ

−−=

rrr

r

rrr

r

ωω

ωωσσ

Из первого уравнения можно исключить производную потокосце-

пления ротора, подставив в него второе уравнение:

,

;))((

))((

2

sr

r

m

sksr

r

rm

ssr

s

sr

r

m

sksr

r

rm

sr

r

m

s

rk

r

m

skss

rks

r

rm

r

m

ss

s

U

L

jILj

L

RL

IRK

dt

Id

L

U

L

jILj

L

RL

IR

L

R

L

jILjU

jI

L

RL

L

R

L

IR

dt

Id

L

rrrrr

r

rrrrr

rrr

rrrr

r

+Ψ−−Ψ+−=

+Ψ−−Ψ++−=

=Ψ−−+

+Ψ−−+Ψ

−−−=

ωωσσ

ωωσ

где

.)(1

2

s

r

m

r

R

L

K +=

Введя обозначения для постоянных времени статорной и роторной

цепей

r

s

R

L

T

R

L

T ==

;

σ

, получим

;)(

;

1

2

rkrsmr

r

sr

m

skss

s

r

sr

rm

sr

s

jTIL

dt

d

T

RL

L

jIjTU

RRL

RL

IK

dt

Id

T

Ψ−−+Ψ−=

Ψ

Ψ−−+Ψ+−=

rrr

r

rrrrr

r

ωω

;

2

3

sr

r

m

p

I

L

ZM

rr

×Ψ=

.

c

MM

dt

d

Z

J

p

−=

ω

(3.13)

Аналогичным образом могут быть получены уравнения АД, запи-

санные относительно других пар векторных переменных, например

относительно токов статора и ротора, тока статора и потокосцепления

намагничивания и т.д.

35

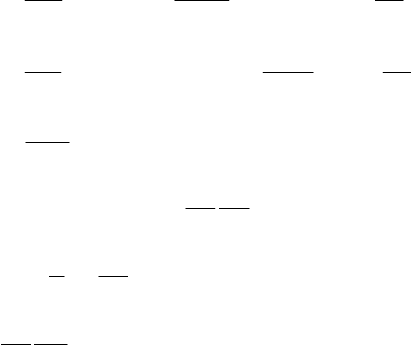
36

k

Заметим, что в данной системе уравнений существенно упрости-

лась модель роторной цепи, выражение для электромагнитного момен-

та. Количество дифференциальных уравнений уменьшилось на едини-

цу. В установившихся режимах работы двигателя все преобразованные

переменные оказываются постоянными величинами. В связи с этим

данная система уравнений очень удобна для расчетов процессов в ма-

шине и для синтеза векторной системы управления в координатах

(d,q). Структурная схема АД в координатах (d,q) изображена на

рис.3.6.

3.5. Уравнения в преобразованных координатах для частных

случаев

Переход от уравнений в ортогональной системе координат (

x,y),

вращающейся с произвольной скоростью

ω

, к уравнениям в ортого-

нальной системе координат

Для системы уравнений, записанной относительно тока статора и

потокосцепления ротора в координатах (

x,y) выполним переход в ор-

тогональную систему координат (

d,q), ориентированную по вектору

потокосцепления ротора. В этом случае

),(

β

α

, неподвижной относительно ста-

тора, осуществляется с помощью подстановки

0

=

k

ω

и замены ин-

декса «

x» на « α », а индекса «y» на «

β

».

ψ

ω

=

k

0,

=

Ψ

rq

rrd

Ψ=Ψ

,

.

;

1

2

d

s

r

sr

rm

dr

d

s

U

R

RL

IK

dt

dI

T +Ψ+−=

qs

IT

+

ψ

ω

;

1

q

s

r

m

dsqr

q

s

U

R

L

ITIK

dt

dI

T +Ψ−−−=

ωω

ψ

sr

RL

;

r

dt

d

T Ψ−=

Ψ

;

r

q

m

I

L

Ψ

+=

ω

ψ

r

s

T

+=

ωωω

dmr

IL+

,I

2

3

qr

r

m

p

L

ZM Ψ=

.

c

MM

dt

d

Z

J

p

−=

ω

(3.14)

S

R

1

rs

KPT +

1

1+PT

L

r

m

J

Z

p

Z

1

sr

sm

RL

2

s

T

rs

KPT +

1

sr

m

RL

L

s

T

S

R

1

r

m

T

L

d

U

d

I

r

ψ

M

c

M

ω

r

ω

s

ω

ψ

ω

ψ

ω

q

U

q

I

r

m

p

L

Z

2

3

Рис.3.6. Структурная схема АД в координатах (d,q)

37

3.6. Математическое описание АД с учетом насыщения цепи

намагничивания

Рассмотренные выше модели АД наиболее широко применяются

для анализа и синтеза процессов в электроприводах с векторным

управлением. Однако если по условиям работы АД потокосцепления

претерпевают существенные изменения, то желателен учет изменения

параметров математической модели, связанный с эффектом насыще-

ния магнитной

системы. Для АД, питаемых от преобразователей час-

тоты (ПЧ), обычно предполагают, что кратность выходных токов в ра-

бочих режимах привода ограничена (составляет не более 2

—3 значе-

ний номинального тока двигателя) и эффектом насыщения цепей рас-

сеяния можно пренебречь. Тем более что, как показывают исследова-

ния, эти изменения достаточно слабо влияют на динамические процес-

сы.

Гораздо более существенно сказывается эффект насыщения цепи

намагничивания. В частности, в рабочих режимах привода с двигате-

лями серии 4А индуктивность намагничивания

может изменяться

до 30 %.

m

L

В асинхронном электроприводе регулирование потокосцепления

требуется в следующих режимах:

1) при работе привода на скоростях, превышающих номинальную

(во 2-й зоне регулирования скорости в режиме постоянства мощности),

происходит ослабление поля;

2) при оптимизации энергетических характеристик привода требу-

ется регулирование потока намагничивания в зависимости от нагруз-

ки;

3) при

оптимизации динамических характеристик привода, в част-

ности быстродействия процессов "в большом", также требуется регу-

лирование потокосцепления.

Для учета эффекта насыщения используется один из следующих

методов: метод статических индуктивностей либо метод динамических

индуктивностей. Последний

— существенно более сложный. Для син-

теза систем управления приводом обычно используется более простой

метод статических индуктивностей, дающий, тем не менее, достаточно

высокую точность в описании динамических процессов. В этом методе

нелинейность цепи намагничивания учитывается статической зависи-

мостью между потокосцеплением и током намагничивания, задавае-

мой таблично или с помощью аналитической аппроксимации:

mmmm

IIL

rr

)(=Ψ или

)(

mm

m

L

I

Ψ

=

r

.

38

В частности, если характеристика намагничивания задана в таб-

личной форме совокупностью точек

NnI

nmnm

,...,1),,(

..

=

Ψ

, то для

ее аппроксимации удобно использовать следующую гладкую аналити-

ческую функцию:

.,...,2,1,)(

1

12

kigI

k

i

mimm

=Ψ=Ψ

∑

=

−

(3.15)

Выбор нечетных степеней полинома (3.15) обеспечивает симмет-

рию характеристики относительно начала координат. В связи с воз-

можным разбросом точек исходного массива данных коэффициенты

полиномиальной аппроксимации

находятся методом наименьших

квадратов. Для удовлетворительной аппроксимации характеристик

намагничивания машин нормального исполнения (в диапазоне изме-

нения

i

g

nommm

Ψ

=Ψ )3,1...0( , включающем зону существенного на-

сыщения) практически достаточно в формуле (3.15) ограничиться

, т.е. 4=k

.)(

7

4

5

3

21 mmmmmm

ggggI Ψ+Ψ+Ψ+Ψ=Ψ

Применение к этой функции процедуры полиномиальной регрес-

сии приводит к следующему матричному уравнению:

,

4

3

2

1

4

3

2

1

7654

6543

5432

4321

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

d

g

cccc

где

;12,....,2,1;,...,2,1;)(

1

2

−==Ψ=

∑

=

kjNnc

N

n

j

mj

;4;)()(

1

12

=Ψ=

∑

=

−

kId

N

n

nmn

j

mj

Nn,

— соответственно порядковый номер и общее количество точек

из массива исходных данных.

В результате решения этого уравнения находятся коэффициенты

полинома

и определяется аналитическая зависимость кривой на-

магничивания.

i

g

Отметим, что для неявнополюсных машин, к которым относится

АД, нелинейный оператор зависит только от амплитуды векторных

переменных и не зависит от их направления. Векторы тока и потокос-

цепления намагничивания остаются при этом сонаправленными.

39

С учетом этого математическая модель АД в преобразованной ор-

тогональной системе координат, вращающейся с произвольной скоро-

стью

, примет вид

k

ω

;)(0

;

rk

r

rr

sk

s

sss

j

dt

d

IR

j

dt

d

IRU

Ψ−+

Ψ

+=

Ψ+

Ψ

+=

r

rr

ωω

ω

;

mrrr

msss

IL

Ψ+=Ψ

rrr

r

σ

;)(

mmmm

IIL

r

=Ψ

;

2

3

sr

r

m

p

I

L

ZM

rr

×Ψ=

.

c

MM

dt

d

Z

J

p

−=

ω

(3.16)

По аналогии с рассмотренными выше преобразованиями модели

(3.9) данную модель также можно преобразовать, записав ее относи-

тельно выбранной пары векторных переменных, например

s

I

r

и

r

Ψ

r

,

и

s

Ψ

r

Ψ

r

и т.д.

В общем случае система нелинейных дифференциальных и алгеб-

раических уравнений (3.16) решается итерационно. Однако если пред-

положить, что между шагами расчета ток намагничивания изменяется

незначительно, то итерации можно исключить.

Иногда для описания процессов в машине удобно пользоваться не

абсолютными, а относительными значениями переменных. Переход к

системам относительных (безразмерных)

переменных и параметров

осуществляется на основе их базисных значений [38].

На рис.3.7 приведена в относительных единицах типовая зависи-

мость

для двигателей серии 4А. )(

mm

L Ψ

40

Виноградов А.Б. Векторное управление электроприводами переменного тока

Подождите немного. Документ загружается.