Виноградов А.Б. Векторное управление электроприводами переменного тока
Подождите немного. Документ загружается.


21
.
00
00
00
cos
3
2
cos
3
2
cos
3
2
coscos
3
2
cos
3
2
cos
3
2
coscos
121212
121212
121212
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
+
c
b
a
C
B
A
r
r
r
I
I
I
I
I
I
L
L
L
MMM
MMM
MMM
γπγπγ
πγγπγ
πγπγγ
(3.4)
Электромагнитный момент асинхронной машины может быть
найден как частная производная по геометрическому углу от общего
запаса электромагнитной энергии машины. Электромагнитная энергия
обмоток асинхронной машины может быть определена по соотноше-
нию
[]
c
I
cb
I
ba
I
aC
I
CB
I
BA
I
Aэ
W Ψ+Ψ+Ψ+Ψ+Ψ+Ψ=
2
1
.
(3.5)
Отсюда электромагнитный момент асинхронного двигателя
p
Z
э
W
M
γ∂
∂
=
,
(3.6)
где — число пар полюсов двигателя.
p
Z
Уравнение движения привода запишется как
dt
d
J
c
MM
ω
=− ,
(3.7)
где М
с
— статический момент нагрузки;
ω
— угловая частота вращения ротора, рад/с;
J — момент инерции электропривода, приведенный к валу двигателя.
Выражения (3.1), (3.4) — (3.7) образуют полную систему уравне-
ний асинхронной машины, представленную в естественных координа-
тах.
Дальнейшее упрощение полученной системы уравнений выполня-
ется следующим образом:
1) из уравнений исключаются фазные значения напряжений (их
использование не всегда удобно
в связи с различными способами
включения обмоток и неопределенностью потенциала общей точки
при отсутствии ее зануления в схеме включения обмоток в "звезду");
2) при выполнении условия симметрии токов из уравнений исклю-
чаются все переменные, относящиеся к одной из фаз статора и ротора,
например к фазе С.
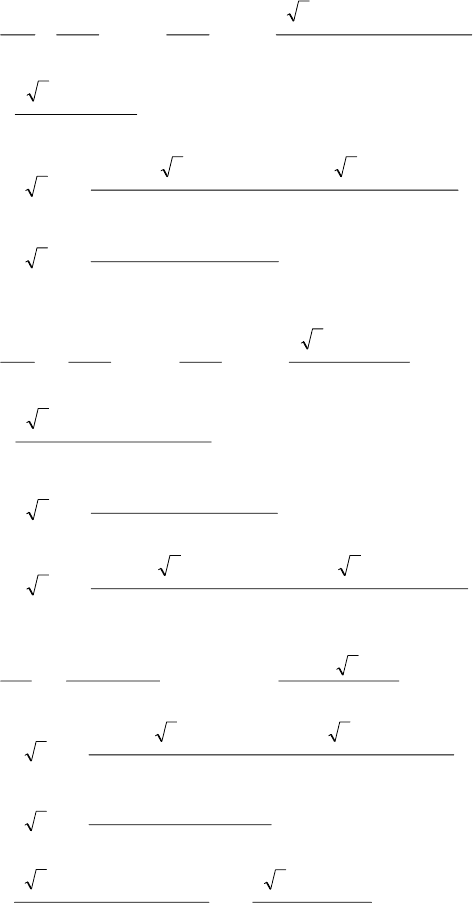
22
Если полученные уравнения записать относительно токов двух фаз
статора и двух фаз ротора, то в результате получим систему следую-
щих уравнений:
;
3
sincos
12
34
3
sincos3cossin3
12
32
3
2
12
36
3
4
2
12
33
3
3
4
3
3
8
b
I
M
r
RZ
r
L
M
a
I
M
)(
r
R)(Z
r
L
M
B
I
M
ZM
A
I
M
r
L
s
RZM
BC
U
M
r
L
AC
U
M
r
L
dt
A
di
p
p
p
p
γγω
γγγγω
ω
ω
−
+
+
−++
+
++
+
−
+−=
;
3
)sincos3()cossin3(
12
32
3
cossin
12
34
3
4
2
12
33
3
2
12
36
3
3
8
3
3
4
b
I
M
r
RZ
r
L
M
a
I
M
Z
r
L
r
R
M
B
I
M
r
L
s
RZM
A
I
M
ZM
BC
U
M
r
L
AC
U
M
r
L
dt
B
di
p
p
p
p
γγγγω
γωγ
ω
ω
++−
+
+
−
+
+
+
−
−−+−=
;
3
2
12
36
3
4
2
12
33
3
cossin
12
34
3
)sincos3()cossin3(
12
32
3
sin3cos
12
2
3
cos
12
4
b
I
M
ZM
a
I
M
S
L
r
RZM
B
I
M
Z
s
L
s
R
M
A
I
M
s
RZ
s
L
M
BC
U
M
M
AC
U
M
M
dt
a
di
p
p
p
p
ω
ω
γωγ
γγγγω
γγ
γ
−
+
−
−
−
+
+
++−
+
+
−
+−=
23
,
3
)sincos3()cossin3(
12
32
3
4
2
12
33
3
sincos
12
34
3
2
12
36
3
cos
12
4
3
sin3cos
12
2
B
I
M
s
RZ
s
L
M
b
I
M
S
L
r
RZM
A
I
M
s
RZ
s
L
M
a
I
M
ZM
BC
U
M
M
AC
U
M
M
dt
b
di
p
p
p
p
γγγγω
ω
γγω
ω
γ
γγ
−++
+
+
−
+
+
−
++
+−
+
=
γ
γ
sin)]22(
cos)[(3
3
2
12
aBbAbBaA
bAaBp
IIIIIIII
IIIIZMM
+++−
−−=
где
2
12
94
3
M
r
L
s
LM −= .
Механическая часть двигателя представляется следующими выра-
жениями:
J
c
MM
dt
d
−
=
ω
,
ω=
γ
p
Z
dt
d
.
Основным недостатком математических моделей в естественных
координатах является их относительная сложность, связанная с нали-
чием периодических коэффициентов в дифференциальных уравнени-
ях.
3.2. Преобразование уравнений асинхронного двигателя
Наличие периодических коэффициентов перед переменными в
уравнениях трехфазной машины заставило искать пути упрощения
системы с тем, чтобы получить дифференциальные уравнения с посто-
янными
коэффициентами. Для этого следует осуществить замену пе-
ременных путем их координатного преобразования.
Предположим, что система уравнений, записанная относительно
новых переменных, описывает какую-то идеализированную асинхрон-

24
ную машину, для которой напряжения, токи и потокосцепления связа-
ны с напряжениями, токами и потокосцеплениями реальной асинхрон-
ной машины искомыми формулами замены переменных (координат-
ных преобразований).
Поскольку дифференциальные уравнения идеализированной асин-
хронной машины не содержат периодических коэффициентов, то мож-
но предположить, что ротор такой машины неподвижен относительно
статора. Действительно, периодические
коэффициенты появляются
вследствие изменения взаимного расположения обмоток статора и ро-
тора.
Далее положим, что статор и ротор идеализированной машины
вращаются в пространстве с произвольной скоростью
k
ω
. Можно
предположить, что величина скорости
k
ω
меняет вид уравнений, уп-
рощая или усложняя их.
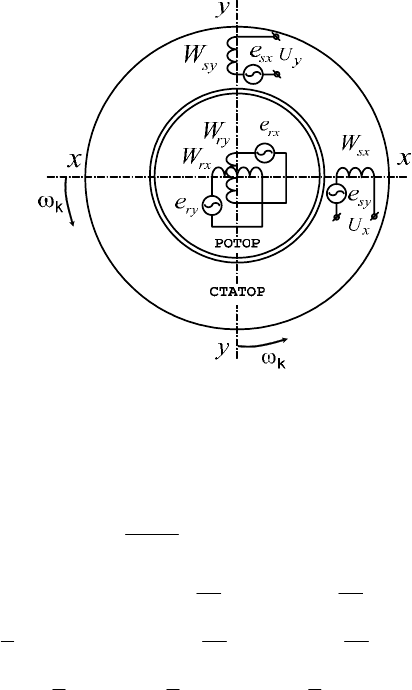
Допустим, что вводимая идеализированная машина двухфазная
(рис.3.2) и эквивалентна трехфазной реальной машине по намагничи-
вающим силам, создаваемым как токами обмотки статора, так и тока-
ми ротора. Обмотки статора и ротора неподвижны друг относительно
друга и расположены вдоль осей координатной системы (
x
, ), при-
чем обе оси в общем случае могут вращаться в пространстве с произ-
вольной скоростью
y
k
ω
. В каждую обмотку включены добавочные
электродвижущие силы
, которые и учитывают вращение ротора от-
носительно статора в реальной асинхронной машине, а также и вели-
чину скорости вращения
e
k
ω
координатной системы ( y
x
, ).
Для преобразования системы дифференциальных уравнений трех-
фазной реальной асинхронной машины необходимо решить две зада-
чи:
- прежде всего необходимо найти искомые формулы записи пере-
менных;
- далее следует, пользуясь формулами преобразования, получить
систему дифференциальных уравнений относительно новых перемен-
ных.
В качестве исходной возьмем систему уравнений в естественных
координатах:
,0;
dt
d
IR
dt
d
IRU
Fr
r
Fr
rr
Fs
s
Fs
ss
Fs
Ψ
+=
Ψ
+=
где
; ; ;
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
C
B
A
Fs
U
U
U
U
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
C
B
A
Fs
s
I
I
I
I
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
c
b
a
Fr
r
I
I
I
I
25
; .
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
Ψ
Ψ
Ψ
=Ψ
C
B
A
Fs
s
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
Ψ
Ψ
Ψ
=Ψ
c
b
a
Fr
r
Рис.3.2. Эквивалентная схема идеализированной асинхронной машины
Уравнение напряжений статорной цепи умножим слева на матри-
цу
координатных преобразований из системы (А,В,С) в систему
(
x,y,z):
1
A
dt
d
AIARUA
Fs
s
Fs
ss
Fs
Ψ
+=
111
,
где
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
π
+ϕ−
π
−ϕ−ϕ−
π
+ϕ
π
−ϕϕ
=
2
1
2
1
2
1
)
3
2
sin()
3
2
sin(sin
)
3
2
cos()
3
2
cos(cos
3
2
1 kkk
kkk
A
;
t
kk
ω=ϕ .
h
z
y
x
Fs
U
U
U
U
UA =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
; .
h
s
sz
sy
sx
Fs
s
I
I
I
I
IA =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
26
Верхний индекс «h» обозначает принадлежность векторной пере-
менной к ортогональной системе координат (
x,y,z), вращающейся с
произвольной скоростью
k
ω
.
Последнюю составляющую преобразованного уравнения статор-
ной цепи рассмотрим подробнее.
Наиболее хорошо физический смысл преобразования производной
виден, если воспользоваться аппаратом представления векторной пе-
ременной в комплексной плоскости (хотя преобразование может быть
получено и непосредственно путем выполнения алгебраических дейст-
вий с компонентами вектора).
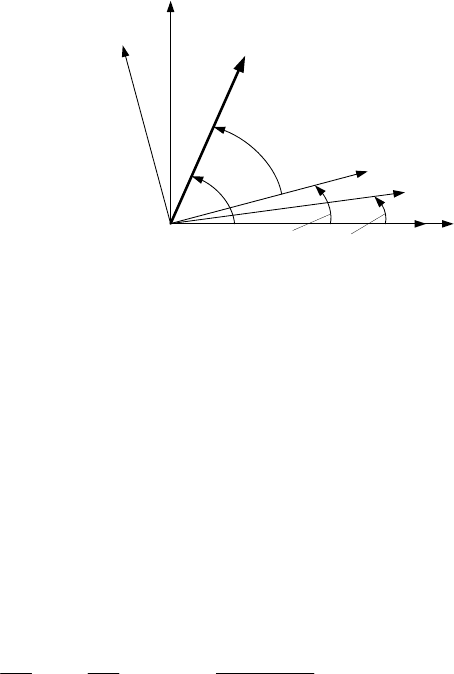
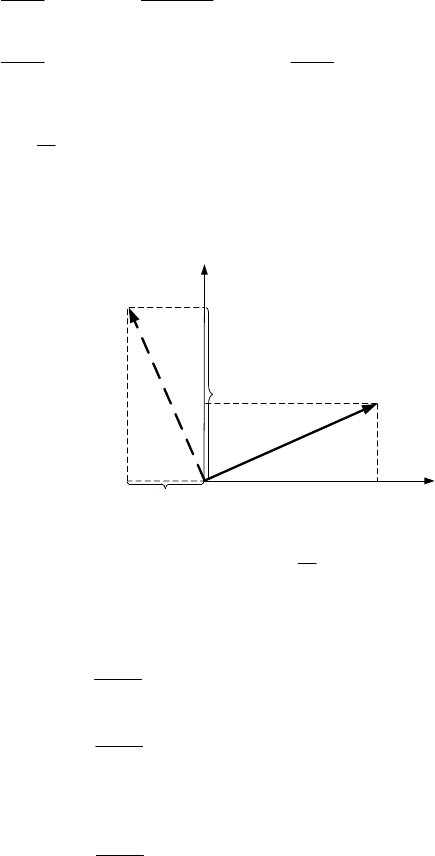
Рассмотрим представление результирующего вектора на ком-
плексной плоскости (рис.3.3).
Im
V
r
h
v
ϕ
F
v
ϕ
x
a
A
Re
t
k
F
h
ωϕ
=
t
ω
ϕ
=
y
Рис. 3.3. Представление результирующего вектора на комплексной плос-
кости
Совместим действительную ось с осью фазы
А, тогда вектор V
r
может быть представлен в следующем виде:
F
h
F
h
h
v
h
v
F
h
F
v
j
h
j
j
jj
j
F
eVeVeVeVeV
ϕϕ
ϕ
ϕ+ϕ
ϕ
⋅=⋅===
rr
;
,
F
h
j
Fh
eVV
ϕ−
=
rr
где
hF
VV
r
r
, — представление вектора V
r
в естественной и преобразо-
ванной системах координат;
— операторы прямого и об-
ратного преобразования из базиса (
А,В,С) в базис (
F
h
F
h
jj
ee
ϕϕ
,
−
y
x
, ).
Для производной вектора
V
r
в базисе (
y
x
,
) можно записать
==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−
F
h
F
h
F
h
j
j
h
j
Fh
e
dt
eVd
e
dt
Vd
dt
Vd
ϕ
ϕ
ϕ
)(
r
r
r
27
=+=
−
F
h
F
h
F
h
j
j
h
j
h
e
dt
ed
Ve
dt
Vd
ϕ
ϕ
ϕ
)
)(
(
r
r
.)(
h
k
h
jj
h
k
j
h
Vj
dt
Vd
eeVje
dt
Vd
F
h
F
h
F
h
r
r
r
r
ωω
ϕϕϕ
+=+=
−
Умножение вектора на оператор j соответствует его повороту на
угол
2
π
(рис. 3.4) и может быть представлено в виде
.
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
x
y
y
x
V
V
V
V
jVj
r
Vj
r
x
V
x
V
y
V
y
x
y
V
−
V
r
Рис.3.4. Поворот оператора j на угол
2
π
С учетом этого преобразованные уравнения статорной цепи в ко-
ординатах (
y
x
, ) примут вид
.
;
sxk
sy
sysy
syk
sx
sxsx
dt
d
IRU
dt
d
IRU
Ψ+
Ψ
+=
Ψ−
Ψ
+=
ω
ω
Уравнение для нулевой последовательности фаз (ось z) запишется
как
.
dt
d
IRU
sz
szsz
Ψ
+=
Аналогичные преобразования, выполненные для уравнений ро-
торной цепи, записанных в естественных координатах ротора, позво-
ляют получить следующие уравнения в преобразованной системе ко-
ординат (
x,y,z):
28
;)(0
ryk
rx
rxr
dt
d
IR Ψω−ω−
Ψ
+=
;)(0
rxk
ry
ryr
dt
d
IR Ψω−ω+
Ψ
+=
.0
dt
d
IR
rz
rzr
Ψ
+=
В векторно-матричной форме записи уравнения статора и ротора
примут вид
,)(0
;
h
rk
h
r
h
rr
h
sk
h
s
h
ss
h
s
B
dt
d
IR
B
dt
d
IRU
Ψ−+
Ψ
+=
Ψ+
Ψ
+=
ωω
ω
где
— матричный коэффициент.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
000
001
010
B
В частном случае симметрии фазных токов из системы исключа-
ются уравнения для нулевой последовательности фаз (по оси z) и они
могут быть компактно записаны в векторной форме:
,)(0
;
rk
r
rr
sk
s
sss
j
dt
d
IR
j
dt
d
IRU
Ψ−+
Ψ
+=
Ψ+
Ψ
+=
r
r
r
r
r
rr
ωω
ω
где
.;;;;
⎥
⎦
⎤
⎢
⎣
⎡
Ψ
Ψ
=Ψ
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
Ψ
Ψ
=Ψ
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
ry
rx
r
ry
rx
r
sy
sx
s
sy
sx
s
y
x
s
I
I
I
I
I
I
U
U
U
rrrrr
Выполним переход в новую систему координат для уравнений по-
токосцеплений статора и ротора. Для потокосцеплений статора выра-
жение
умножим на
A
Ψ
()
t
K
ω
cos
3
2
,
B
Ψ
— на
(
)
0
120cos
3
2
−t
K
ω
,
— на
C
Ψ
(
)
0
120cos
3
2
+t
K
ω
. Затем сложим все три уравнения. По-
сле преобразования получим потокосцепление статора по оси
x
:

29
()
,
2
3
ms1211 rxsxrxsxsx
ILILIMIML +=+−=Ψ
где
mss
LLMLL
+
=
−=
σ
11
— полная эквивалентная индуктивность
фазы статора (
— полная индуктивность рассеяния фазы статора (с
учетом двух других его фаз);
s
L
σ
12
2
3
ML
m
=
— эквивалентная взаимная
индуктивность).
Аналогичным путем можно получить потокосцепление статора по
оси
:
y
.
rymsyssy
ILIL +=Ψ
Для нулевой последовательности фаз (по оси z) будем иметь
szssz
IL
0
σ
=Ψ ,
где
— индуктивность рассеяния фазы статора для нулевой после-
довательности фаз. Она немного меньше полной индуктивности рас-
сеяния фазы статора
, так как не включает в себя потоки рассеяния
статора, сцепленные с двумя другими фазами статора. Для индуктив-
ностей рассеяния можно записать
, где — состав-
ляющая полной индуктивности рассеяния статора, образованная маг-
нитными потоками рассеяния фазы статора, имеющими магнитную
связь с другими обмотками статора. Соответственно
— состав-
ляющая полной индуктивности рассеяния статора, образованная маг-
нитными потоками рассеяния фазы статора, не имеющими магнитной
связи с другими обмотками статора.
0
s
L
σ
s
L
σ
m
sss
LLL
σσσ
+=
0 m
s
L
σ
0
s
L
σ
Проводя аналогичные преобразования выражений потокосцепле-
ний ротора, найдем выражения для потокосцеплений ротора соответ-
ственно по осям
x,y,z:
,
;
;
0
rzrrz
symryrry
sxmrxrrx
IL
ILIL
ILIL
σ
=Ψ
+=Ψ
+=Ψ
где
mrr
LLMLL
+
=
−=
σ
12
— полная эквивалентная индуктивность
фазы ротора (
— полная индуктивность рассеяния фазы
ротора, включающая составляющие от потоков рассеяния ротора, не
сцепленных и сцепленных с другими фазами ротора).
m
rrr
LLL
σσσ
+=
0
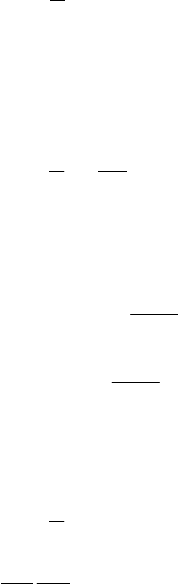
30
Выражение для электромагнитного момента, записанное относи-
тельно преобразованных токов статора и ротора, будет иметь вид
.)(
2
3
rysxrxsymp
IIIILZM −=
На основе уравнений связи можно записать формулу для момента
относительно любой пары векторных переменных, составленной из
следующего набора:
mrsmrs
III ΨΨΨ
r
r
r
r
r
r
,,,,, . Например, относительно
тока статора и потокосцепления ротора
.)(
2
3
sxrysyrx
r
m
p
II
L
L
ZM Ψ−Ψ=
Дополнив приведенные уравнения уравнением движения, получим
полную систему уравнений, описывающую асинхронную машину в
преобразованных координатах. В векторно-матричной форме записи
;)(0
;
h
rk
h
r
h
rR
h
sk
h
s
h
sS
h
s
B
dt
d
IR
B
dt
d
IRU
Ψ−+
Ψ
+=
Ψ+
Ψ
+=
ωω
ω
;
;
h
sM
h
rR
h
r
h
rM
h
sS
h
s
ILIL
ILIL
+=Ψ
+=Ψ
;)(
2
3
rysxrxsymp
IIIILZM −=
c
MM
dt
d
Z
J
p
−=
ω
,
(3.8)
где
; ;
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
0
00
0
00
s
s
s
S
L
L
L
L
σ
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
0
00
0
00
r
r
r
R
L
L
L
L
σ
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
000
0
00
m
m
M
L
L
L ; ;
— матрицы индуктивностей статора, ротора, намагничивания, актив-
ных сопротивлений статора и ротора.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
s
s
s
S
R
R
R
R
00
0
00
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
r
r
r
R
R
R
R
R
00
0
00
