Vij D.R. Handbook of Applied Solid State Spectroscopy

Подождите немного. Документ загружается.

6.5 INTERACTIONS OF CRYSTAL FIELD SPLIT IONS

6.5.1. Introductory Remarks

In the preceding sections, we considered crystal field effects for non-

interacting rare earth ions. However, the crystal field states are usually subject

to interactions with phonons, spin fluctuations, conduction electrons (or more

generally charge carriers), etc., which limit the lifetime of the crystal field

states, thus the observed crystal field transitions exhibit line broadening. This

has major consequences for the cross-section formulae, which have been

derived to interpret spectroscopic experiments. More specifically, in the

neutron cross-section formulae (6.53) and (6.54) the G-function describing the

energy conservation has to be replaced by a Lorentzian with a finite linewidth

whose temperature dependence is characteristic of the particular type of

interaction. Moreover, if the rare earth ions are coupled by the exchange

interaction, the crystal field excitations can propagate through the lattice. All

these effects will be discussed in the following subsections.

6.5.2 Interaction with Phonons

Theoretical models of the effects of lattice vibrations in distorting the crystal

field have been suggested since the early 1930s by Heitler and Teller [57],

Kronig [58], and van Vleck [59]. A more detailed and general approach was

developed later by Orbach [60]. His main idea was to treat the spin-lattice

interaction as a dynamic crystal field effect, which produces deformations of

the equilibrium charge configuration of the surrounding ions. Orbach

proposed to expand the crystal field potential V in powers of the fluctuating

strain H caused by the lattice vibrations [60]:

(0) (1) 2 (2)

VV V V

  

(6.56)

where V

(0)

is the static term, V

(1)

and V

(2)

represent the dynamical part of the

magnetic ion-lattice interaction generated by the strain in first- and second-

order, respectively. In these calculations the spin-orbit coupling has to be

included. The terms V

(n)

in equation (6.56) turned out to be of the same order

as the static V

(0)

. These calculations made it possible to evaluate the spin-

lattice relaxation time in terms of a few constants. However, the additional

distinction of whether the rare earth ion has an odd (Kramers ion) or an even

number of electrons must be made.

Orbach considered in detail one-phonon (or direct) and two-phonon

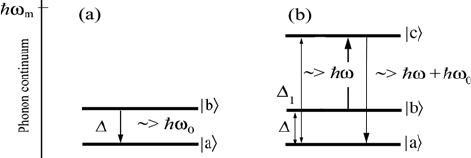
processes. Suppose that the ground state J-multiplet of the rare earth ion is

split into two low-lying states |a² and |b², energetically separated from the

excited state |c². In a direct process a single transition ¨ is made from |b² to |a²

and a phonon of energy



is emitted (see Figure 6.16a). This process will

6.5 Interactions of Crystal Field Split Ions

287

6. Crystal Field Spectroscopy

be dominant only at the lowest temperatures, for most rare earth compounds

typically around 1 K. The spin-lattice relaxation time

for the direct process

in an external field H exhibits the typical behavior

~ T

–1

–4

and W

~ T

for the Kramers and non-Kramers ions, respectively.



system and an intermediate transition from |b² to |c² occurs. To complete the





then emitted as shown in Figure 6.16b. In this case the spin-lattice relaxation

time

turns out to be W

~ exp(¨

T).

Figure 6.16 Schematic diagram for the direct (a) and the two-phonon (b) process. Only the

anti-Stokes process is shown.

Z= is the maximum allowed phonon energy in the phonon

continuum.

The basic difference between the Raman (see Section 6.3.3) and the

Orbach processes is that in the former process “virtual” transitions are

involved, i.e., the crystal field state |c² has an energy ¨

! k

that lies

outside the continuum of allowed phonon frequencies (compare Figures 6.6

and 6.16b. For this case the relaxation times turn out to be

–9

and W

–7

for the Kramers and non-Kramers ions, respectively. The relaxation time of

the Raman process is independent of a magnetic field. Note that the Raman

process dominates the Orbach process at high temperatures. For further

discussion and bibliography the reader is referred to some classical textbooks

(see, e.g., [1]).

6.5.3 Interaction with Conduction Electrons

The interaction with the charge carriers is by far the dominating relaxation

mechanism in metallic rare earth compounds. The corresponding linewidth

(T) increases almost linearly with temperature according to the well-known

Korringa law [61]:

(T) 4S(g1)

J(J 1) N(E

)  j

 T ,

(6.57)

where g denotes the Landé factor, N(E

) the density-of-states of the charge

carriers at the Fermi energy E

, and j

the exchange integral between the

charge carriers and the 4f electrons of the rare earth ions. The inclusion of

crystal field effects slightly modifies the low-temperature limit of equation

(6.57) according to the theory of Becker, Fulde, and Keller [62]:

process a transition from |c² to |a² occurs and a phonon of energy

Z + Z is

In the two-phonon process a phonon of energy

Z is absorbed by the spin

288

6.5 Interactions Of Crystal Field Split Ions



(T) 2j

coth

§

©

¨

·

¹

¸



 M

)

exp

1





izk



¬

«

 M

)

exp

1

§

©

¨

·

¹

¸

kz j

º

¼

»

(6.58)

where



ij i j



summed over the Brillouin zone. For a noninteracting Fermi liquid we have

ij ij

"( ) N (E )

FZ S Z==.

(6.59)

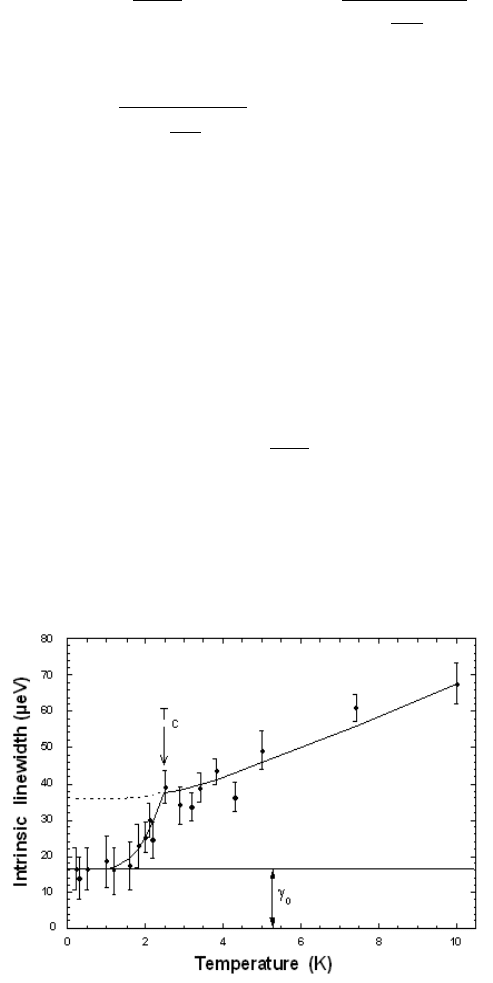
The situation is anomalous for superconducting compounds because the

Cooper pairing of the charge carriers creates an energy gap ' below the

superconducting transition temperature T

, thus crystal field excitations with



there is no interaction with the charge carriers. For an isotropic gap, the

intrinsic linewidth in the superconducting state is then given by

(T) *

(T) exp 





®

¯



¾

¿

(6.60)

This means that *

(T<<T

) § 0, and line broadening sets in just below T

where the superconducting gap opens. The exponential temperature

dependence of *

(T) was nicely demonstrated in the first neutron

spectroscopic study on the classical superconductor La

1–x

[63] (see

Figure 6.17).

Figure 6.17 Observed linewidth of the crystal field transition at 0.68 meV in La

0.997

0.003

vs. temperature. The superconducting transition temperature T

is indicated by an arrow. The

solid curve results from a fit to eqs. (58) and (60) (after [63]) for T > T

and T < T

respectively. The calculations assume a constant additive contribution J

due to local structural

F" Z

F"( Z

E  E , and F"( Z) is the imaginary part of the susceptibility

energy Z2' do not have enough energy to span the gap, and consequently

distortions.

289

6. Crystal Field Spectroscopy

6.5.4. Magnetic Exchange Interaction

In extended, undiluted systems the exchange coupling between the rare earth

ions is often of the same order of magnitude as the crystal field interaction,

thus it has to be considered in the total spin Hamiltonian: H = H

+ H

. The

most widely used approximation for the exchange interaction is the

Heisenberg model:

ij i j

HJ  

JJ . (6.61)

The random phase approximation is then used to express the generalized

dynamical susceptibility tensor in the following form [64]:

)()(J21

)(

),(

ZF

(6.62)

where J(q) is the Fourier transform of the exchange couplings J

, q the

wavevector of the propagating magnetic excitation, and

(Z) the single-ion

susceptibility:



(Z) gP



 E

n,m

p





(6.63)

Here E

and *

denote the energy and the wavefunction of the crystal field

states, respectively, and

the Boltzmann population factor. The magnetic

excitation energies are determined by the poles of equation (6.62) which

yields the dispersion relation



p

(6.64)

where ' = E

–E

and M is the transition matrix element between the two

crystal field states.

Figure 6.18 shows neutron spectroscopy data observed for the

(1)

crystal field transition in PrNi

[46] which gave rise to a well-defined peak in

the PCS spectra of Figure 6.8. The full dispersion measured for different

wavevectors q allowed to determine the exchange coupling parameters

parallel and perpendicular to the hexagonal c-axis. Figure 6.18 nicely shows

the flattening of the dispersion curve with increasing temperature which is due

Z

Z(q) '2'MJ(q) p

290

to the increasing thermal population of the excited state (see equation (6.64)).

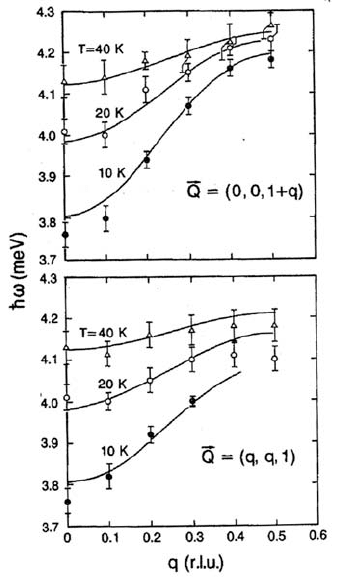
6.6 Crystal Field Effects Related

Figure 6.18 Dispersion of the *

(1)

crystal field transition in PrNi

as a function of Q

scanned parallel and perpendicular to the hexagonal c-axis for different temperatures. The lines

represent fits to eq. (64) (after [46]).

6.6 CRYSTAL FIELD EFFECTS RELATED

TO HIGH-TEMPERATURE SUPERCONDUCTIVITY

6.6.1 Introductory Remarks

The discovery of high-temperature superconductivity in the copper-oxide

perovskites [65] has given rise to a huge amount of materials research. In

particular, there have been myriad publications reporting on the change of the

superconducting properties upon ion substitution at various sites in these

compounds. For the compounds YBa

the surprising observation was

made that the superconducting transition temperature T

is essentially

unchanged upon replacing the Y

ions by paramagnetic rare earth (R

) ions,

in contrast to conventional superconductors, for which paramagnetic ions

usually have a large detrimental effect on superconductivity. It is therefore

important to achieve a detailed understanding of the low-energy electronic

properties which define the magnetic ground state of the R

ions. In

particular, information on the crystal field interaction at the R site is highly

desirable, for the following reasons:

291

6. Crystal Field Spectroscopy

(i) For many high-T

compounds, superconductivity and long-range three-

dimensional magnetic ordering of the R ion sublattice coexist at low

temperatures (with the exception of R = Ce and R = Pr which have a drastic

detrimental effect on superconductivity). An understanding of both the

nature of the magnetic ordering and its apparent lack of influence on T

requires a detailed knowledge of the crystal field states of the R ions.

(ii) In most high-T

compounds the R ions are situated close to the

superconducting copper-oxide planes where the superconducting carriers

are located, thus the crystal field interaction at the R sites constitutes an

ideal probe of the local symmetry as well as the local charge distribution

of the superconducting CuO

planes and thereby monitors directly

changes of the carrier concentration induced by doping. This property

results from the short-range nature of the leading fourth- and sixth-order

terms in the crystal field potential.

(iii) The temperature dependence of the intrinsic linewidths of crystal field

transitions reflects essentially the density-of-states associated with the

charge carriers at the Fermi energy. Linewidth studies can therefore

reveal information about the opening as well as the symmetry of the

energy gap.

In the following subsections we focus on aspects (ii) and (iii), which

provide crucial information on two important issues of the phenomenon of

high-T

superconductivity, namely the inhomogeneous evolution of the

superconducting state upon doping and the existence of the so-called

pseudogap, respectively.

6.6.2 The Crystal Field as a Local Probe: Evidence for

Materials Inhomogeneities

One of the most interesting aspects of the superconductivity in the compounds

of type YBa

is the relation between the superconducting transition

temperature T

and the oxygen stoichiometry x [66]. Annealed systems exhibit

a two-plateau structure of T

as visualized in Figure 6.19f. Charge transfer

from the CuO chains to the CuO

planes certainly plays a crucial role in the

oxygen vacancy-induced suppression of superconductivity in YBa

, and

this should manifest itself in the oxygen stoichiometry dependence of the

observed crystal field energy spectra. This is exemplified for ErBa

Figure 6.20 [51]. When going from x = 6 to x = 7, the transitions B, D, E shift

slightly to lower energies and the transitions A, F, G move up to higher

energies, whereas the energy of the transition C remains unchanged. By

analyzing the crystal field parameters on the basis of equation (6.18) it could

be shown that the observed shifts of the crystal field transitions are due to

both structural changes and charge transfer effects [51]. In particular, it was

found that a charge of 0.07 |e|/O is transferred into the planes when going

292

6.6 Crystal Field Effects Related

from x = 6 to x = 7, which means that about 28% of the created holes go into

the planes. Similar conclusions have been obtained for the related compound

HoBa

[67]. These results show an almost linear dependence of the

charge transferred as a function of x. This is in agreement with the results of

neutron diffraction experiments on ErBa

which give evidence for a

linear decrease of the c-axis upon hole doping [68], but it is in contrast to the

conclusions of bond valence sum arguments derived in similar experiments on

YBa

where the two-plateau structure of T

has been suggested to be

due to the nonlinearity of the hole transfer into the planes [66].

Figure 6.21 displays the low-energy part of the energy spectra of

ErBa

upon increased resolution conditions [69], which show that the

lowest crystal field transition A is actually built up of three different

components, A

, A

, and A

, whose main characteristics can be summarized

as follows:

(i) Intensities: The individual components A

have maximum weight close to

x = 7.0, x = 6.5, and x = 6.0, respectively. With the crystal field

interaction being a local probe, there is no doubt that these substructures

originate from different local environments of the Er

ions which

obviously coexist in the compound ErBa

(ii) Energies: Whereas all the crystal field transitions are independent of

energy for oxygen content x  6.5 within experimental error, they shift

slightly when going from x § 6.5 to x § 6.0. This may be due to the

structural discontinuities at the orthorhombic to tetragonal phase

transition at x § 6.4.

(iii) Linewidth: As visualized in Figure 6.19d, the intrinsic linewidths of the

transitions A

are much smaller for oxygen contents where these

transitions individually reach their maximum weight, namely for x § 6.0,

6.5, and 7.0.

All these facts and their interpretation provide clear experimental evidence

for cluster formation. It is tempting to identify the three clusters associated

with the transitions A

, A

, and A

by two local regions of metallic (T

§ 90 K,

§ 60 K) and a local region of semiconducting character, respectively [69].

Figures 19a,b,c show the fractional proportions of the three cluster types that

exhibit a continuous behavior versus oxygen content x, consistent with the

earlier conclusion that the transfer of holes into the CuO

planes is linearly

related to the oxygenation process [51]. Furthermore, the continuous increase

of the metallic states A

and A

can explain the increase of the

superconducting volume fraction as observed by magnetic susceptibility

measurements [68] when the oxygen content is raised from x = 6 to x = 7. It

should be mentioned that these results have been nicely confirmed by PSR

experiments [70] showing the coexistence of superconductivity and

antiferromagnetism at low doping.

293

6. Crystal Field Spectroscopy

Figure 6.19 (a,b,c) Proportions (expressed as a percentage) of the lowest-lying crystal field

transitions A

of ErBa

as a function of the oxygen content x. The full, dashed, and broken

lines refer to geometrical probability functions as explained in the text. The dotted lines mark

the critical concentration for bond percolation. d) Intrinsic linewidths of the crystal field

transitions A

at T=10 K. e) Mean cluster length versus oxygen content x determined by a

Monte Carlo simulation [75]. f) Superconducting transition temperature T

versus oxygen

content x for ErBa

(after [50]).

Figure 6.20 Energy spectra of neutrons scattered from ErBa

at T=10 K. The lines

indicate the x dependence of the observed crystal field transitions (after [51]).

294

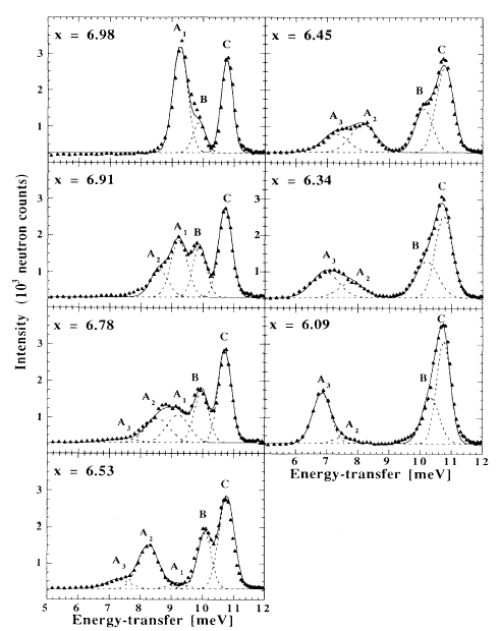
6.6 Crystal Field Effects Related

Figure 6.21 Energy spectra of neutrons scattered from ErBa

at T = 10 K. The full lines

are the result of a least squares fitting procedure. The broken lines indicate the subdivision into

individual crystal field transitions (after [69]).

Our current understanding of the superconducting properties of

ErBa

(and more generally all the RBa

compounds) involves a

percolation mechanism of electric conductivity as discussed in both

theoretical [71] and experimental [72] work. For x = 6 the system is a perfect

semiconductor. When adding oxygen ions into the chains, holes are

continuously transferred into the CuO

planes. By this mechanism the number

of local regions with metallic character (associated with the crystal field

transition A

) rises, which can partially combine to form larger regions. For

some critical concentration a percolative network is built up, and the system

undergoes a transition from the semiconducting to the conducting state (with

§ 60 K). Upon further increasing of hole concentration a second (different)

type of metallic cluster (associated with the crystal field transition A

) is

formed, which start to attach to each other and induce a transition into another

conducting state (with T

§ 90 K) at the percolation limit.

For a two-dimensional square structure the critical concentration for bond

percolation is p

= 50% [73]. From the fractional proportions of A

and A

295

6. Crystal Field Spectroscopy

displayed in Figures 6.19a,b,c we can then immediately determine the critical

oxygen concentrations for the transitions from the semiconducting to the

§ 60 K superconducting state and to the T

§ 90 K superconducting state to

be x

= 6.40 and x

= 6.84, respectively, which is in excellent agreement with

the observed two-plateau structure of T

(see Figures 6.19a,b,f). For three-

dimensional structures, on the other hand, the critical concentration for bond

percolation is 20% (face-centered cubic) < p

< 30% (simple cubic) [73],

resulting in 6.21 < x

< 6.31 and 6.64 < x

< 6.73, which is inconsistent with

the observed two-plateau structure of T

. This reinforces the well known fact

that the superconductivity in the perovskite-type compounds has indeed a

two-dimensional character.

Combined statistical and geometrical considerations may be useful to

understand the x-dependent profiles of the fractional proportions of the three

cluster types visualized in Figures 19a,b,c. A local symmetry model [74] was

developed that defines specific probabilities P

(y) to have, for a given oxygen

content x = 6 + y, k of the four oxygen chain sites (0,1/2,0), (1,1/2,0),

(0,1/2,1), and (1,1/2,1) nearest to the R

ion occupied:

(y)



©

¨



¹

¸

(1  y)

4k

, 0d k d 4 .

(6.65)

The fractional proportion of the cluster type A

exhibits the behavior

predicted by the probability function P

(y) (i.e., all the oxygen chain sites

being occupied). Similarly, the fractional proportions of the cluster types A

and A

follow the sum of the probability functions P

(y) + P

(y) (i.e., one or

two empty oxygen chain sites) and P

(y) + P

(y) (i.e., one or no oxygen chain

site occupied), respectively. The above probability functions are shown in

Figures 6.19a,b,c by lines which excellently reproduce the experimental data.

The x-dependent linewidth of the crystal field transitions allows one to

estimate the size of the clusters, since a line broadening is due to structural

inhomogeneities and gradients in the charge distribution, which occur

predominantly at the border lines between different cluster types. For a cluster

of mean length L (in units of the lattice parameter a) in the (a,b)-plane the

fraction of unit cells at the border of the cluster and inside the cluster is

4(L–1)/L

and [(L – 2)/L]

, respectively. In a first approximation the total

linewidth is then given by [75]

(L 2)

 4(L 1)

§

©

¨

·

¹

¸

*

ª

¬

«

º

¼

»

(6.66)

where *

is the intrinsic linewidth for infinite cluster size (i.e., for x = 6 and

x = 7 exactly realized), and 'E corresponds to the energetic separation of the

crystal field transitions A

for two coexisting cluster types. More specifically,

from Figure 6.21 we derive 'E = E(A

) – E(A

) § 1.0 meV and 'E = E(A

) –

296