Vij D.R. Handbook of Applied Solid State Spectroscopy

Подождите немного. Документ загружается.

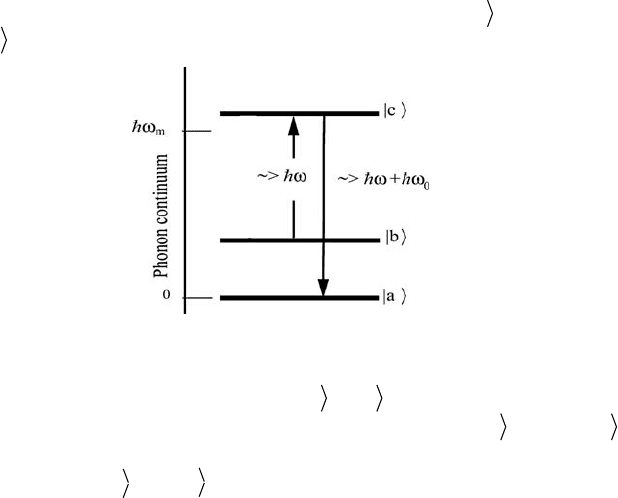
6.3 Experimental Techniques

when the photon causes an induced transition from state | b to an excited

state

| c whose energy is higher than the Debye energy k

BTD. This excitation

Figure 6.6 A schematic diagram for the anti-Stokes Raman process.

is followed by a second virtual transition | c o| a , as indicated in Figure 6.6.

This gives an indirect two-stage transfer of an ion from state

| b to state | a ,

which could become an important relaxation process if the direct process

between the states

| a and | b is negligible.

Raman processes are governed by two conservation laws as in neutron

spectroscopy (see equations (6.37) and (6.38)): energy conservation and

momentum conservation, i.e., the energy and momentum of the scattered

radiation and the elementary excitation created (absorbed) in the interaction

process equals the energy and momentum of the exciting photon. As the

photon wavevector is about 10

times smaller than a typical reciprocal lattice

vector, only excitations at the center of the Brillouin zone are observed by

Raman scattering.

The Raman spectroscopy obeys characteristic selection rules, which reflect

the symmetry properties of the elementary excitations. Crystal field excita-

tions are forbidden if the rare earth ions occupy a center of inversion. This

explains the difficulties of detecting crystal field excitations in hole-doped,

high-temperature superconductors of type RBa

7–x

. On the other hand,

this drawback does not exist for electron-doped, high-temperature

superconductors as reported, e.g., for Raman spectroscopy studies carried out

for the compounds R

CuO

(R = Pr, Nd, Sm) [28, 29] and R

2 – x

CuO

[40].

Other interesting examples are the elpasolites Cs

NaRX

(R = rare earth;

X = Cl, Br), which will be highlighted in Section 6.4.1. For Cs

NaTbCl

most comprehensive data set was collected with a total of 125 levels, which

include states originating from 10 of the 17 terms and 36 of the 87 multiplets

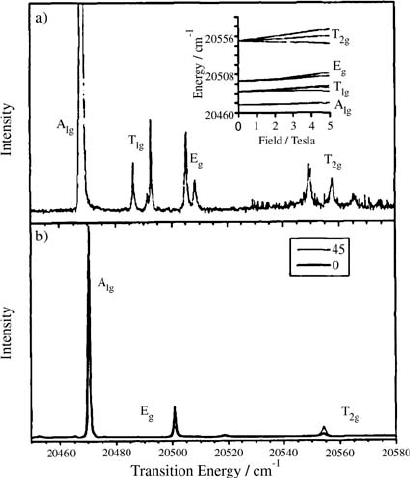
[41]. Figure 6.7 displays transitions in the

-multiplet obtained by

luminescence spectroscopy, emphasizing the ability to resolve Zeeman

splittings as well as the effect of linear polarizations.

277

6. Crystal Field Spectroscopy

Figure 6.7 Two-photon excitation spectra of a single crystal of Cs

NaTbC1

, at ~ 6 K (a) in the

presence of a 4.5 T field along [110] and (b) in zero-field but in two linear polarizations making

the angle indicated to [001]. The inset shows the experimental field dependence of the Zeeman

energies (after [41]).

The calculation of intensities of the observed Raman-active crystal field

transitions is a nontrivial task. This is in contrast to neutron spectroscopy

where the intensities of crystal field transitions are directly proportional to the

square of the magnetic dipole matrix elements (see equations (6.53) and

(6.54)). Since Raman scattering is always at least a two-step process, it

involves intermediate states that are often not known, thus approximate

models have to be employed for the calculation of transition matrix elements

[42]. On the other hand, as a laser is usually used for Raman experiments, the

specific polarization of the exciting source can be exploited to obtain extra

information from the spectra as exemplified in [28].

6.3.4 Point-Contact Spectroscopy

Electrical point-contact spectroscopy (PCS) is a technique to study the

interaction mechanism of electrons with all kinds of elementary excitations in

metals. Small constrictions between two metals show deviations from the

linearity governed by Ohm’s law. The nonlinearity is a measure of the

inelastic scattering of the conduction electrons, where the applied voltage

defines the energy scale for the interaction process. Yanson [43] discovered

these nonlinearities in the I–V characteristics of microcontacts between metals

278

6.3 Experimental Techniques

and used them for a direct microscopic measurement of the energy

dependence of the interaction between conduction electrons and quasiparticle

excitations such as phonons, magnons, paramagnetic impurities, crystal field

excitations, and so on. For the ballistic electron transport (i.e., both the

inelastic and the elastic mean free paths are larger than the contact size) the

second derivative d

V/dI

of the voltage with respect to the current turns out

to be proportional to the spectral function of the interaction process. For

instance, in the case of the electron-phonon interaction, the spectral function is

the well known Eliashberg function D

F [44]. In case of crystal field

interactions the point-contact spectra show additional maxima associated with

the allowed crystal field transitions.

As an example we quote the splitting of the Pr

ions which were directly

observed in the hexagonal van Vleck paramagnet PrNi

[45]. Figure 6.8

displays the corresponding PCS spectra, which exhibit several maxima and

kinks marked by arrows, however, only the peaks at 4.6, 13.6, and 29.4 meV

can be associated with crystal field transitions (see [46] and Section 6.5.1),

whereas the peaks at 9.2 and 18.5 meV are due to electron-phonon interaction.

The PCS was subsequently used to measure the Zeeman splitting of the crystal

field excitations in external magnetic fields up to 20 T for the same compound

[47].

Figure 6.8 Microcontact PrNi

spectra (after [45]).

Nowadays the PCS has become a standard technique for the study of the

electron-phonon interaction in conductors (for a review see [48]), but at

present it seems to be limited to simple metals and intermetallic compounds.

279

6. Crystal Field Spectroscopy

The limitation of the PCS as a spectroscopic tool is due to the fact that the

contact diameter has to be smaller than the inelastic electron mean free path,

which is hardly fulfilled in most of the strongly correlated electron systems, so

that the data analysis becomes ambiguous and complicated. Moreover, the

PCS technique cannot discriminate a priori between crystal field and electron-

phonon interactions, i.e., a proper identification of the observed PCS spectra

strongly relies on the availability of other spectroscopic data.

6.4 DETERMINATION OF CRYSTAL FIELD

PARAMETERS FROM EXPERIMENTAL DATA

In this section we present a simple crystal field problem in order to exemplify

the way in which the crystal field parameters can be determined from

spectroscopic data. We choose the insulating compound series Cs

NaRBr

(R = rare earth) called (bromo-)elpasolites, which were investigated by

several experimental techniques, so that we can compare the results and

thereby obtain information about the performance of the different

experimental methods.

The crystal field is the dominant interaction for the rare earth elpasolites,

since no magnetic ordering is observed down to the lowest temperatures, thus

exchange effects can be neglected. Moreover, the elpasolites have a cubic

crystal structure with the R

ions situated at the sites of octahedral symmetry,

i.e., each R

ion is hexacoordinated by six nearest Br

–

ions. Thus the crystal

field problem is rather simple with only two independent crystal field

parameters (see equation (6.9)).

Figures 6.9 and 6.10 show the results of neutron spectroscopic

investigations for Cs

NaErBr

) [25]. The cubic crystal field splits the

16-fold degenerate ground state

15/2

-multiplet of the Er

ion into two

doublets

and *

and three quartets *

(1)

, *

(2)

and

(3)

. The low-

temperature spectra of Figure 6.9 give evidence for two inelastic lines A and

B at 3.0 and 5.8 meV, respectively, that can be attributed to crystal field

transitions out of the ground state. Upon raising the temperature the intensity

of line B decreases as expected (because of the decreasing Boltzmann

population factor), whereas the intensity of line A increases slightly because

of an excited crystal field transition that occurs accidentally at the same

energy. For Er

the higher lying crystal field states usually have very small

matrix elements for transitions out of the ground state, thus their energies can

be determined only in connection with excited-state transitions. This is

demonstrated in Figure 6.10 by lines C and D at 21 and 25 meV, respectively,

whose intensities clearly increase with increasing temperature.

6.4.1 A Simple Two-Parameter Crystal Field Problem

280

Figure 6.9 Low-energy spectra of neutrons scattered from Cs

NaErBr

observed with use of a

triple-axis spectrometer. The analyzer energy and the modulus of the scattering vector were set

to E

=13.7 meV and Q =1.25 Å

-1

, respectively (after [25]).

Figure 6.10 Medium-energy spectra of neutrons scattered from Cs

NaErBr

with E

=13.7 meV

and Q = 2.4 Å

-1

(after [25]).

281

6.4 Determination of Crystal Field Parameters

6. Crystal Field Spectroscopy

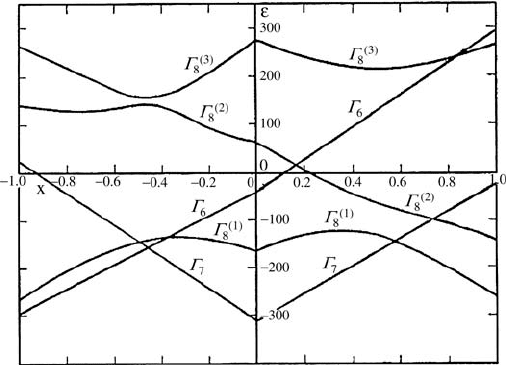
These experiments tell us immediately that the crystal field splitting



crystal field states by their correct representations, an inspection of the energy

level sequence in terms of the parameters W and x (see equation (6.10)) is

most useful. Figure 6.11 offers at least two sets of parameters that are

compatible with the spectroscopic data, namely x § –0.6 with a

ground

state and x § 0.65 with a

)1(

* ground state, both with W > 0. This means that a

unique identification of the crystal field states is not possible by consideration

of the energy splittings alone. In addition, we have to consider the intensities

of the observed crystal field transitions (as tabulated in [38]), which in the

present case unambiguously favor the parameter set {x § 0.65, W > 0}. By

doing this, we can completely reconstruct the crystal field level scheme of

NaErBr

from the spectroscopic data (see Figure 6.12). The resulting

crystal field parameters, mainly determined from neutron (N) and optical (O)

spectro-scopic measurements, which are presently available for the rare earth

bromo-elpasolites, are listed in Table 6.1. The agreement between N and O is

rather good for R = Ho, R = Tm, and R = Yb, with a maximum deviation of

0.5 meV for all crystal field levels (which can readily be calculated from

equation (6.9)). For R = Pr there is a discrepancy for the highest crystal field

whereas an energy of 77 meV was derived from the luminescence spectrum.

The discrepancies for R = Tb can be explained by the fact that neutron

spectroscopy was able to establish only the low-energy part of the crystal field

level structure.

Figure 6.11 Eigenvalues of Eq. (10) (after [12]) for Er

level * , which is located at 55 meV in the neutron-scattering experiments,

comprises three low-lying states in the energy range 0 <

Z < 6 meV,

separated from two high-lying states at Z > 20 meV. In order to identify the

282

Figure 6.12 Crystal field level scheme of Cs

NaErBr

. The arrows and corresponding labels

denote the transitions observed by neutron spectroscopy.

We may conclude that both N and O spectroscopies have their merits for

the determination of crystal field splittings in the ground state J-multiplet of

rare earth compounds; however, the correct identification of the observed

crystal field states is more reliable in neutron spectroscopic experiments, since

no approximations have to be applied to calculate the transition matrix

elements. On the other hand, optical spectroscopies have distinct advantages

for measurements of intermultiplet crystal field excitations. Finally, the data

for R = Yb show that a reliable determination of crystal field parameters from

thermodynamic magnetic data is usually not possible.

The crystal field parameters listed in Table 6.1 are found to follow nicely

the extrapolation scheme of equation (6.32). However, there is a slight

increase of the parameters from the light to the heavy rare earth ions. This was

explained in terms of dipolar polarizability and covalency [49], which seem to

have an increased relative importance for the heavy rare earth compounds.

In this section we exemplify the crystal field procedure for a metallic

compound with low symmetry at the rare earth site, for which the use of

neutron spectroscopy is indispensable. This is particularly true for the rare

earth-based high-temperature superconductors for which early attempts to

unravel and to parametrize the crystal field interaction by other techniques

failed completely. We choose as an example the compound ErBa

6.4.2 A Complicated Many-Parameter Crystal Field Problem

283

6.4 Determination of Crystal Field Parameters

6. Crystal Field Spectroscopy

Table 6.1 Crystal field parameters and of the elpasolites Cs

NaRBr

determined by

different experimental techniques (N: neutron spectroscopy; O: optical spectroscopies; M:

magnetic susceptibility).

) which has orthorhombic symmetry at the Er

site, i.e., the crystal

field Hamiltonian is defined by equation (6.12) with nine independent

parameters. The crystal field splits the 16-fold degenerate ground state

multiplet of Er

into eight Kramers doublets. All seven crystal field

transitions out of the ground state have been observed by neutron

spectroscopy as shown in Figure 6.13 [50, 51], thus the crystal field level

splitting is completely established. Yet the crystal field states have to be

characterized by their proper representations, which is a highly nontrivial task

in view of the large number of adjustable crystal field parameters. This is due

to the difficult problem of any nonlinear least squares fitting procedure of

choosing reasonable start values of the fitting parameters, which, however,

can be achieved as described below.

B (meV)

Technique Ref.

Ce 0.162 ± 0.002 0 N A

(

–

1.32 ± 0.06

)

·10

(

1.39 ± 0.13

)

·10 N A

(–1.93 ± 0.10)·10 (1.20 ± 0.29)·10 O B

(

–

7.6 ± 0.2

)

·10

(

–

7.2 ± 0.3

)

·10 N A

(

2.1 ± 0.2

)

·10

(

–

1.5 ± 0.4

)

·10 N A

(2.96 ± 0.05)·10 (–1.35 ± 0.17)·10 O C

(

–

1.3 ± 0.1

)

·10

(

1.5 ± 0.3

)

·10 N A

(

–

6.2 ± 0.5

)

·10

(

–

1.4 ± 0.2

)

·10 N A

(–6.56 ± 0.08)·10 (–1.58 ± 0.10)·10 O B

(

8.1 ± 0.3

)

·10

(

1.8 ± 0.1

)

·10 N A

(

3.0 ± 0.4

)

·10

(

–

4.2 ± 0.8

)

·10 N A

(3.32 ± 0.18)·10 (–4.06 ± 2.18)·10 O B

(

–

3.1 ± 0.1

)

·10

(

1.1 ± 0.3

)

·10 N A

(–3.53 ± 0.31)·10 0 O B

–2.13·10 1.38·10

M D

A: Furrer A and Güdel H U 1997 Phys. Rev. B 56 15062–72

B: Tanner P A, Ravi Kanth Kumar V V, Jayasankar C K, and Reid M F 1994 J. Alloys Compd. 215 349–70

C: Berry A J, McCaw C S, Morrison I D, and Denning R G 1996 J. Lumin. 66 & 67 272–7

D: Urland W 1979 Z. Naturforsch. 34a 1507–11

15/2

–

–2

–3

–5

–6

284

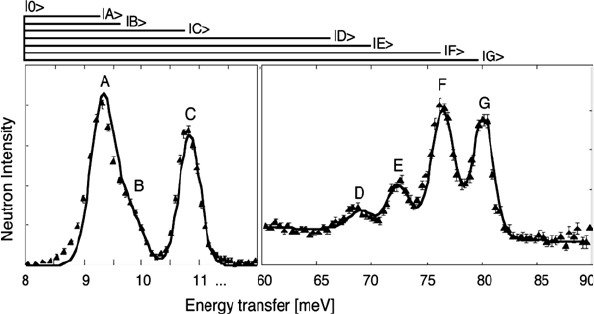
Figure 6.13 Energy spectra of neutrons scattered from ErBa

at T=10 K. The lines

represent the calculated spectra. The arrows on top of the figure denote the observed ground

state transitions (after [50]).

The coordination polyhedra of Er

in ErBa

formed by the nearest

neighbors (eight oxygen ions) as well as by the next-nearest neighbors (eight

copper ions) are slightly distorted cubes. Thus we expect the overall features

of the crystal field potential to be reasonably described in a first

approximation by cubic point symmetry, which limits the number of

disposable parameters to two as for Cs

NaErBr

discussed in the preceding

section. Now we make use of the fact that the crystal field transitions occur in

a low-energy window (



< 12 meV, lines A–C) and in a high-energy

window (65 <



< 82 meV, lines D–G), i.e., the crystal field splitting is

characterized by four low-lying doublets and four doublets at much higher

energies. Inspection of Figure 6.11 tells us that this particular situation can

only be realized for the parameter x § –0.45 with either W > 0 or W < 0 (note

that in cubic symmetry six doublets merge into three quartets). When

considering the intensities, the parameter set with W < 0 has to be discarded,

thus the set {x § –0.45, W > 0} gives us a good estimate of the dominant

crystal field parameters

and B

. In a second step we make use of equation

(6.30) in order to arrive at reasonable values for the remaining

“orthorhombic” crystal field parameters. After having determined

reasonable start values of the crystal field parameters as outlined above, a

least squares fitting procedure is then applied to the observed energy spectra,

which usually converges successfully to a final, appropriate set of crystal field

parameters (see [51]).

Another useful scheme to predict crystal field parameters in metallic

systems is based on the extended point-charge model (see Section 6.2.2.2). As

shown by Mesot and Furrer [52], the crystal field parameters of ErBa

calculated from equation (6.24), with the inverse screening length adjusted to

N = 1.25 Å

–1

, provide values very close to the fitted ones.

285

6.4 Determination of Crystal Field Parameters

6. Crystal Field Spectroscopy

In order to check the reliability of the derived crystal field parameters it is

important to calculate various thermodynamic properties with the help of

equations (6.33)–(6.34) and to compare the results with experimental data.

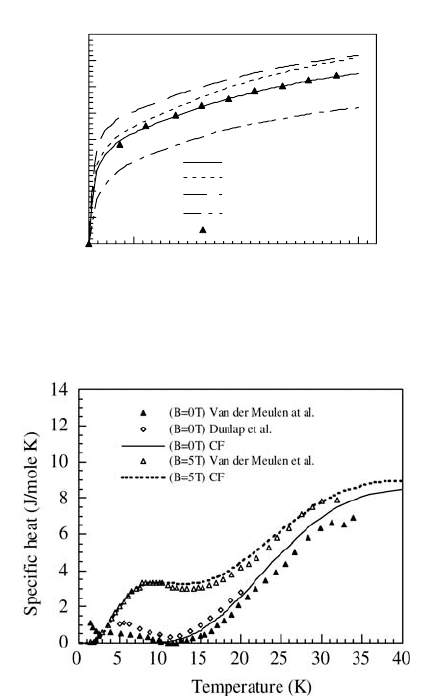
Figures 6.14 and 6.15 [51] show the good agreement between high-field

magnetization [53] and specific heat [54, 55] measurements of powder

samples and calculations using the crystal field parameters determined by

neutron spectroscopy [51]. Moreover, the crystal field interaction reduces the

zero-field moment of Er

in ErBa

drastically below the free ion value

of 9 P

. A mean-field calculation based on equation (6.33) yields 4.2 P

, in

agreement with the value derived from Mössbauer experiments [56].

0 5 10 15 20 25 30

<M>=1/3(M

)

- CF

<M>- Roeland et al.

B [Tesla]

M [µ

]

Figure 6.14 High-field magnetization observed and calculated for ErBa

(after [51]).

Figure 6.15 Schottky anomaly of the heat capacity observed and calculated for ErBa

(after [51]).

286