Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

11.3 Two-Way ANOVA and Factorial Designs 429

have levels 1 and 2. The y-axis contains the means of response (IL-10). The

circles in both plots correspond to the cell means.

For example, in Fig. 11.3a x-axis has two levels of factor HEC. The means

of IL-10 for LPS=1 are connected by the red line, while the means for LPS=2

are connected by the black line. When the lines on the plots are approximately

parallel, the interaction between the factors is absent. Thus, the interaction

plots serve as exploratory tools to check if the interaction term should be in-

cluded in the ANOVA model. Note that some interaction between LPS and

HEC is present (the lines are perfectly parallel); however, this interaction was

found not statistically signiﬁcant (p-value of 0.2334).

Next, we visualize the ANOVA fundamental identity.

%insulin.m continued

SSA = table{2,2}; SSB = table{3,2}; SSAB=table{4,2};

SSE=table{5,2}; SST = table{6,2};

%Display the budget of Sums of Squares

H=figure;

set(H,’Position’,[400 400 400 400]);

y=[0 0 1 1];

hold on

h1=fill([0 SST SST 0],y,’c’);

y=y+1;

h2=fill([0 SSA SSA 0],y,’y’);

h3=fill([0 SSB SSB 0]+SSA,y,’r’);

h4=fill([0 SSAB SSAB 0]+SSA+SSB,y,’g’);

h5=fill([0 SSE SSE 0]+SSA+SSB+SSAB,y,’b’);

y=y+1;

h6=fill([0 SST SST 0],y,’w’);

hold off

legend([h1 h2 h3 h4 h5],’SST’,’SSA’,’SSB’,’SSAB’,’SSE’,...

’Location’,’NorthWest’)

title(’Sums of Squares’)

Figure 11.4 shows the budget of sums of squares in this design. It is graph-

ical representation of SST

= SS A +SSB +SS AB + SSE. It shows the con-

tributions to the total variability by the factors, their interaction and the er-

ror. Note that the sum of squares attributed to LPS (in yellow) is not visi-

ble in the plot. This is because its relative contribution to SST is very small,

0.0073/49.8539

<0.00015.

The ANOVA table and both Figs. 11.3 and 11.4 are generated by ﬁle

insulin.m. For a Bayesian solution of this example consult insulin.odc.

430 11 ANOVA and Elements of Experimental Design

0 10 20 30 40

0.5

1.5

2.5

Sums of Squares

SST

SSA

SSB

SSAB

SSE

Fig. 11.4 Budget of sums of squares for Insulin example.

11.4 Blocking

In many cases the design can account for the variability due to subjects or to

experimental runs and focus on the variability induced by the treatments that

constitute the factor of interest.

Example 11.5. Blocking by Rats. A researcher wishes to determine whether

or not four different testing procedures produce different responses to the con-

centration of a particular poison in the blood of experimental rats. To mini-

mize the inﬂuence of rat-to-rat variability, the biologist selects four rats from

the same litter. Each of the four rats is given the same dose of poison per gram

of body weight and then samples of their blood are tested by the four test-

ing methods administered in random order. There are 4 different litters each

containing 4 rats for a total of 16 animals involved.

concentration = [9.3 9.4 9.2 9.7 9.4 9.3 9.4 9.6 ...

9.6 9.8 9.5 10.0 10.0 9.9 9.7 10.2];

procedure = [1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4];

litter = [1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4];

[p,table,stats,terms]=anovan(concentration,{procedure,litter},...

’varnames’,char(’Procedure’,’Rat’))

%p = 1.0e-003

% 0.8713

% 0.0452

%table =

11.5 Repeated Measures Design 431

% ’Source’ ’Sum Sq.’ ’d.f.’ ’Singular?’ ’Mean Sq.’

% ’Procedure’ [0.3850] [ 3] [ 0] [ 0.1283]

% ’Rat’ [0.8250] [ 3] [ 0] [ 0.2750]

% ’Error’ [0.0800] [ 9] [ 0] [ 0.0089]

% ’Total’ [1.2900] [15] [ 0] []

% ’F’ ’Prob>F’

% [14.4375] [8.7127e-004]

% [30.9375] [4.5233e-005]

% [] []

In the above code, procedure is the factor of interest and litter is the block-

ing factor. Note that both the

procedure and litter factors are highly signiﬁ-

cant at levels 0.0008713 and 0.0000452, respectively. We are interested in sig-

niﬁcant differences between the levels of

procedure factor, but not between the

litters or individual animals. However, it is desirable that the blocking factor

turns out to be signiﬁcant since in that case we will have accounted for sig-

niﬁcant variability attributed to blocks and separated it from the variability

attributed to the test procedures. This makes the test more accurate.

To emphasize the beneﬁts of blocking, we provide a nonsolution by treating

this problem as a one-way ANOVA layout. This time, we fail to ﬁnd any signif-

icant difference between the testing procedures (p-value 0.2196). Clearly, this

approach is incorrect on other grounds: the condition of independence among

the treatments, required for ANOVA, is violated.

[p,table,stats] = anova1(concentration,procedure)

%p = 0.2196

%table =

%’Source’ ’SS’ ’df’ ’MS’ ’F’ ’Prob>F’

%’Groups’ [0.3850] [ 3] [0.1283] [1.7017] [0.2196]

%’Error’ [0.9050] [12] [0.0754] [] []

%’Total’ [1.2900] [15] [] [] []

In many cases the blocking is done by batches of material, animals from

the same litter, by matching the demographic characteristics of the patients,

etc. The repeated measures design is a form of block design where the blocking

is done by subjects, individual animals, etc.

11.5 Repeated Measures Design

Repeated measures designs represent a generalization of the paired t-test to

designs with more than two groups/treatments. In repeated measures designs

432 11 ANOVA and Elements of Experimental Design

the blocks are usually subjects, motivating the name “within-subject ANOVA”

that is sometimes used. Every subject responds at all levels of the factor of

interest, i.e., treatments. For example, in clinical trials, the subjects’ responses

could be taken at several time instances.

Such designs are sometimes necessary and have many advantages. The

most important advantage is that the design controls for the variability be-

tween the subjects, which is usually not of interest. In simple words, subjects

serve as their own controls, and the variability between them does not “leak”

into the variability between the treatments. Another advantage is operational.

Compared with factorial designs, repeated measures need fewer participants.

In the repeated measures design the independence between treatments

(experimental conditions) is violated. Naturally, the responses of a subject are

dependent on each other across treatments.

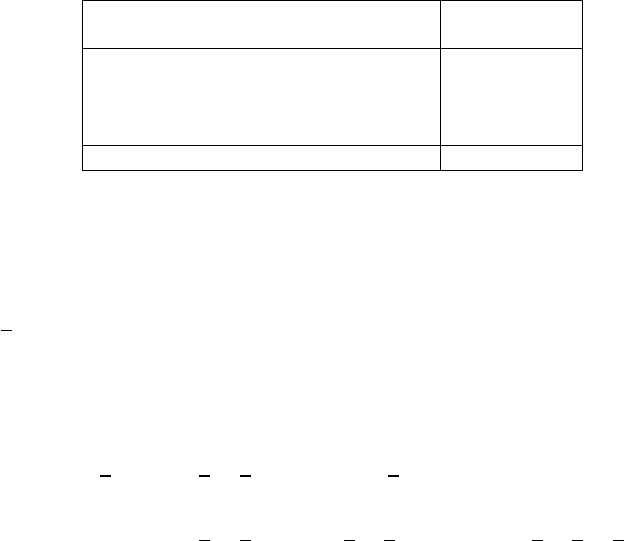
ANOVA Table for Repeated Measures

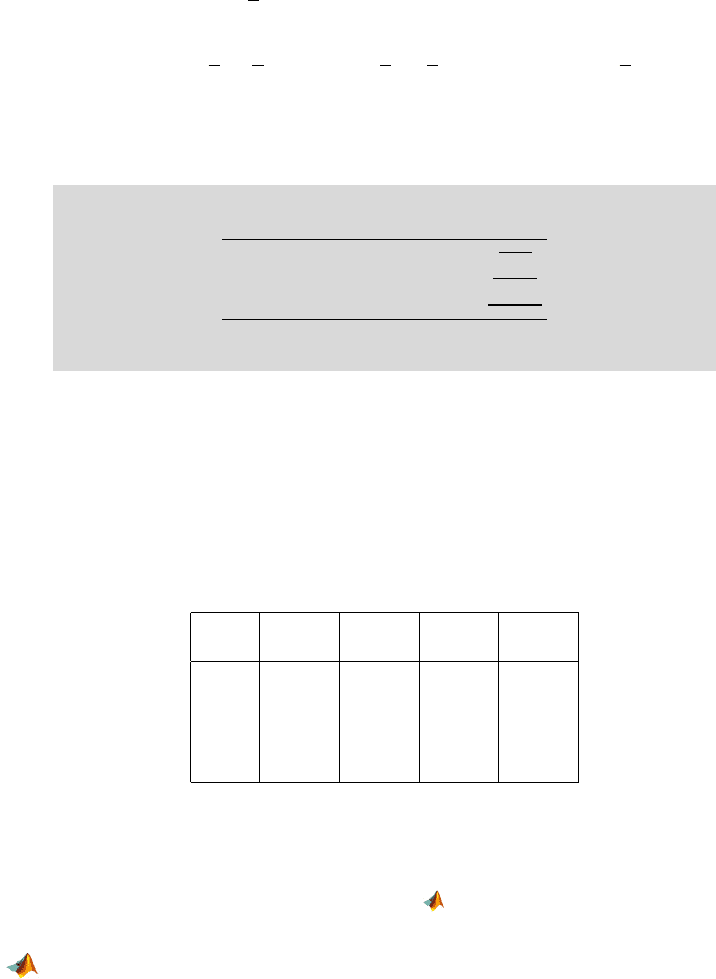
Subject 1 2 . . . n Treatment total

Treatment

1 y

··· y

1·

2 y

··· y

2·

··· ··· ···

k y

··· y

k·

Subject total y

·1

·2

··· y

·n

··

The ANOVA model is

i j

=µ +α

+β

+²

i j

, i =1, . .., k; j =1,..., n,

in which the hypothesis H

: α

=0, i =1,..., k, is of interest.

SST

=SS

BetweenSub jects

+SS

W ithinSub jects

=SSB +[SS A +SSE].

Equivalently,

The degrees of freedom are split as

−1 =(n −1) +n(k −1) =(n −1) +[(k −1) +(n −1) ·(k −1)].

The ANOVA table is

i=1

j=1

i j

−

)

= k

j=1

(

. j

−

)

i=1

j=1

i j

−

. j

)

= k

j=1

(

. j

−

)

i=1

(

−

)

i=1

j=1

i j

−

. j

)

In the repeated measures design, total sum of squares

SST

i j

−

)

partitions in the following way:

11.5 Repeated Measures Design 433

Source DF SS MS F p

Factor A k −1 SSA MS A =

SSA

k−1

MS A

MSE

P(F

k−1,(k−1)(n−1)

)

Subjects B n

−1 SSB MSB =

SSB

n−1

MSB

MSE

P(F

n−1,(k−1)(n−1)

)

Error (k

−1)(n −1) SSE MSE =

SSE

(k−1)(n−1)

Total kn −1 SST

The test statistic for Factor A (H

: α

= 0, i = 1,..., k) is F

= MSA/MSE

for which the p-value is p

= P(F

k−1,(k−1)(n−1)

> F

). Usually we are not inter-

ested in F

= MSB/MSE; however, its signiﬁcance would mean that blocking

by subjects is efﬁcient in accounting for some variability thus making the in-

ference about Factor A more precise.

Example 11.6. Kidney Dialysis. Eight patients each underwent three differ-

ent methods of kidney dialysis (Daugridas and Ing, 1994). The following values

were obtained for weight change in kilograms between dialysis sessions:

Patient Treatment 1 Treatment 2 Treatment 3

1 2.90 2.97 2.67

2 2.56 2.45 2.62

3 2.88 2.76 1.84

4 1.73 1.20 1.33

5 2.50 2.16 1.27

6 3.18 2.89 2.39

7 2.83 2.87 2.39

8 1.92 2.01 1.66

Test the null hypothesis that there is no difference in mean weight change

among treatments. Use

α =0.05.

%dialysis.m

weich=[ 2.90 2.97 2.67 ;...

2.56 2.45 2.62 ;...

2.88 2.76 1.84 ;...

1.73 1.20 1.33 ;...

2.50 2.16 1.27 ;...

3.18 2.89 2.39 ;...

2.83 2.87 2.39 ;...

1.92 2.01 1.66 ];

subject=[1 2 3 4 5 6 7 8 ...

1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8];

treatment = [1 1 1 1 1 1 1 1 ...

2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3];

[p table stats terms] = ...

anovan(weich(:),{subject, treatment},’varnames’,...

434 11 ANOVA and Elements of Experimental Design

{’Subject’ ’Treatment’} )

%’Source’ ’Sum Sq.’ ’d.f.’ ’Mean Sq.’ ’F’ ’Prob>F’

%’Subject’ [5.6530] [ 7] [0.8076] [11.9341][6.0748e-005]

%’Treatment’ [1.2510] [ 2] [0.6255] [ 9.2436][ 0.0028]

%’Error’ [0.9474] [14] [0.0677] [] []

%’Total’ [7.8515] [23] [] [] []

SST = table{5,2}; SSE = table{4,2};

SSTr = table{3,2}; SSBl = table{2,2};

SSW = SST - SSBl;

Since the hypothesis of equality of treatment means is rejected (p-val =

0.0028), one may look at the differences of treatment effects to ﬁnd out which

means are different. Command

multcompare(stats,’dimension’,2) will per-

form multiple comparisons along the second dimension,

Treatment, and pro-

duces:

%1.0000 2.0000 -0.1917 0.1488 0.4892

%1.0000 3.0000 0.2008 0.5413 0.8817

%2.0000 3.0000 0.0521 0.3925 0.7329

This output is interpreted as α

−α

∈[−0.1917,0.4892], α

−α

∈[0.2008,

0.8817] and

−α

∈ [0.0521,0.7329] with simultaneous conﬁdence of 95%.

Thus, by inspecting which interval contains 0 we conclude that treatment

means 1 and 2 are not signiﬁcantly different, while the mean for treatment

3 is signiﬁcantly smaller from the means for treatments 1 or 2. For a Bayesian

solution consult

dialysis.odc.

0 1 2 3 4 5 6 7 8

0.5

1.5

2.5

Sums of Squares

SST

SSBl

SSW

SSTr

SSE

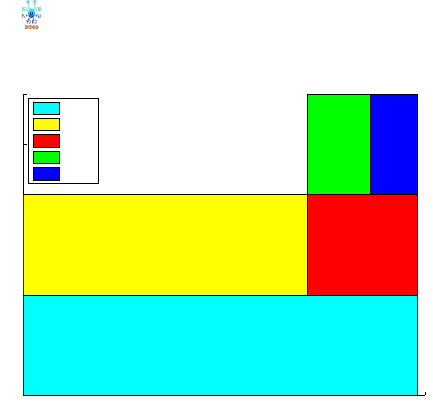
Fig. 11.5 Budget of sums of squares for Kidney Dialysis example.

Figure 11.5 shows the budget of sums of squares. Note that the SSTr and

SSE comprise SSW (Sum of Squares Within), while SSBl (variability due to

11.5 Repeated Measures Design 435

subjects) is completely separated from SSTr and SSE. If the blocking by sub-

jects is ignored and the problem is considered as a one-way ANOVA, the sub-

ject variability will be a part of SSE leading to wrong inference about the

treatments (Exercise 11.16).

11.5.1 Sphericity Tests

Instead of the independence condition, as required in ANOVA, another condi-

tion is needed for repeated measures in order for an inference to be valid. This

is the condition of sphericity or circularity. In simple terms, the sphericity as-

sumption requires that all pairs of treatments be positively correlated in the

same way. Another way to express sphericity is that variances of all pairwise

differences between treatments are the same.

When an F-test in a repeated measures scenario is performed, many sta-

tistical packages (such as SAS, SPSS) automatically generate corrections for

violations of sphericity. Examples are the Greenhouse–Geisser, the Huynh–

Feldt, and lower-bound corrections. These packages correct for sphericity by

altering the degrees of freedom, thereby altering the p-value for the observed

F-ratio.

Opinions differ about which correction is the best, and this depends on

what one wants to control in the analysis. An accepted universal choice is to

use the Greenhouse–Geisser correction,

. Violation of sphericity is more

serious when

is smaller. When ²

>0.75 Huynh–Feldt correction ²

recommended.

An application of Greenhouse–Geisser’s and Huynh–Feldt’s corrections,

and ²

, respectively, is provided in the script bellow ( circularity.m)

in the context of Example 11.16.

weich=[ 2.90 2.97 2.67 ; 2.56 2.45 2.62 ;...

2.88 2.76 1.84 ; 1.73 1.20 1.33 ;...

2.50 2.16 1.27 ; 3.18 2.89 2.39 ;...

2.83 2.87 2.39 ; 1.92 2.01 1.66 ];

n = size(weich,1); %number of subjects, n=8

k = size(weich,2); %number of treatments, k=3

Sig = cov(weich); %covariance matrix of weich

md = trace(Sig)/k; %mean of diagonal entries of Sig

ma = mean(mean(Sig)); %mean of all components in Sig

mr = mean(Sig’); %row means of Sig

A = (k

(md-ma))^2;

B = (k-1)

(sum(sum(Sig.^2))-2

sum(mr.^2)+k^2

ma^2);

epsGG = A/B %Greenhouse-Geisser epsilon 0.7038

epsHF = (n

(k-1)

epsGG-2)/((k-1)

((n-1)-(k-1)

epsGG))

%Huynh-Feldt epsilon 0.8281

%Corrections based on Trujillo-Ortiz et al. functions

436 11 ANOVA and Elements of Experimental Design

%epsGG.m and epsHF.m available on MATLAB Central.

F = 9.2436; %F statistic for testing treatment differences

p = 1-fcdf(F,k-1,(n-1)

(k-1)) %original pvalue 0.0028

padjGG = 1-fcdf(F,epsGG

(k-1),epsGG

(n-1)

(k-1)) %0.0085

padjHF = 1-fcdf(F,epsHF

(k-1),epsHF

(n-1)

(k-1)) %0.0053

Note that both degrees of freedom in the F statistic for testing the treat-

ments are multiplied by correction factors, which increased the original p-

value. In this example the corrections for circularity did not change the orig-

inal decision of rejection of hypothesis H

stating the equality of treatment

effects.

11.6 Nested Designs*

In the factorial design two-way ANOVA, two factors are crossed. This means

that at each level of factor A we get measurements under all levels of factor B,

that is, all cells in the design are nonempty. In Example 11.4, two factors,

HEC and LPS, given at two levels each (“yes” and “no”), form a 2

×2 table with

four cells. The factors are crossed, meaning that for each combination of levels

we obtained observations. Sometimes this is impossible to achieve due to the

nature of the experiment.

Suppose, for example, that four diets are given to mice and that we are

interested in the mean concentration of a particular chemical in the tissue.

Twelve experimental animals are randomly divided into four groups of three

and each group put on a particular diet. After 2 weeks the animals are sac-

riﬁced and from each animal the tissue is sampled at ﬁve different random

locations. The factors “diet” and “animal” cannot be crossed. After a single di-

etary regime, taking measurements on an animal requires its sacriﬁce, thus

repeated measures designs are impossible.

The design is nested, and the responses are

i jk

=µ +α

+β

j(i)

+²

i jk

, i =1,... , 4; j =1, ...,3; k = 1,...,5,

where

µ is the grand mean, α

is the effect of the ith diet, and β

j(i)

is the effect

of animal j, which is nested within treatment i.

For a general balanced two-factor nested design,

i jk

=µ +α

+β

j(i)

+²

i jk

, i =1,.. . , a; j =1,..., b; k =1,..., n,

the identiﬁability constraints are

=0, and for each i,

j(i)

=0. The

ANOVA identity SST

=SS A +SSB(A) +SSE is

11.6 Nested Designs* 437

i=1

j= 1

k=1

i jk

− y

...

)

= bn

i=1

i..

− y

...

)

i=1

j=1

i j.

− y

...

)

i=1

j=1

k=1

i jk

− y

i j.

)

The degrees of freedom are partitioned according to the ANOVA identity

as abn

−1 =(a −1) +a(b −1) +ab(n −1). The ANOVA table is

Source DF SS MS

A a −1 SS A MSA =

SS A

a−1

B(A) b −1 SSB MSB =

SSB

a(b−1)

Error ab(n −1) SSE MSE =

SSE

ab(n−1)

Total abn −1 SST

Notice that the table does not provide the F-statistics and p-values. This

is because the inferences differ depending on whether the factors are ﬁxed or

random.

The test for the main effect H

: all α

= 0 is based on F = MS A/MSE if

both factors A and B are ﬁxed, and on F

= MSA/MSB(A) if at least one of the

factors is random. The test H

: all β

j(i)

= 0 is based on F = MSB(A)/MSE in

both cases. In the mouse-diet example, factor B (animals) is random.

Example 11.7. Suppose that the data for the mouse-diet study are given as

Diet 1 2 3 4

Animal 1 2 3 1 2 3 1 2 3 1 2 3

k =1 65 68 56 74 69 73 65 67 72 81 76 77

k =2 71 70 55 76 70 77 74 59 63 75 72 69

k =3 63 64 65 79 80 77 70 61 64 77 79 74

k =4 69 71 68 81 79 79 69 66 69 75 82 79

k =5 73 75 70 72 68 68 73 71 70 80 78 66

There are 12 mice in total, and the diets are assigned 3 mice each. On each

mouse 5 measurements are taken. As we pointed out, this does not constitute

a design with crossed factors since, for example, animal 1 under diet 1 differs

from animal 1 under diet 2. Rather, the factor animal is nested within the

factor diet. The following script is given in

nesta.m.

yijk =[...

65 68 56 74 69 73 65 67 72 81 76 77 ;...

71 70 55 76 70 77 74 59 63 75 72 69 ;...

63 64 65 79 80 77 70 61 64 77 79 74 ;...

69 71 68 81 79 79 69 66 69 75 82 79 ;...

73 75 70 72 68 68 73 71 70 80 78 66 ];

438 11 ANOVA and Elements of Experimental Design

a = 4;

b = 3;

n = 5;

%matrices of means (y..., y

i.., y

ij.)

yddd = mean(mean(yijk))

ones(n, a

yijd = repmat(mean(yijk), n, 1)

%yidd---------------------

m=mean(yijk);

mm=reshape(m’, b, a);

c=mean(mm);

d=repmat(c’,1,b);

e=d’;

yidd = repmat(e(:)’,n,1)

SST = sum(sum((yijk - yddd).^2) ) %2.3166e+003

SSA = sum(sum((yidd - yddd).^2) ) %1.0227e+003

SSB

A = sum(sum((yijd - yidd).^2) ) %295.0667

SSE = sum(sum((yijk - yijd).^2) ) %998.8

MSA = SSA/(a-1) %340.9111

MSB

A = SSB

A/(a

(b-1)) %36.8833

MSE = SSE/(a

(n-1)) %20.8083

%A fixed B(A) random //// 0r A random B(A) random

FArand = MSA/MSB

A %9.2430

pa = 1- fcdf(FArand, a-1, a

(b-1)) %0.0056

A = MSB

A/MSE %1.7725

a = 1- fcdf(FB

A, a

(b-1), a

(n-1)) %0.1061

Figure 11.6 shows the budget of sums of squares for this example.

From the analysis we conclude that the effects of factor A (diet) were sig-

niﬁcant (p

= 0.0056), while the (speciﬁc) effects of factor B (animal) were not

signiﬁcant (p

=0.1061).

Remarks. (1) Note that the nested model does not have the interaction term.

This is because the animals are nested within the diets. (2) If the design is

not balanced, the calculations are substantially more complex and regression

model should be used whenever possible.

11.7 Power Analysis in ANOVA

To design a sample size for an ANOVA test, one needs to specify the signif-

icance level, desired power, and a precision. Precision is deﬁned in terms of

ANOVA variance

and population treatment effects α

coming from the null