Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

11.2 One-Way ANOVA 419

then the contrast (1, −1,−3,3) is 2C

−C

. Any set of k −1 orthogonal

contrasts perfectly partitions the SSTr. If SSC

(

)

then

SST r

=SSC

+SSC

+···+SSC

k−1

This gives a possibility of simultaneous testing of any subset

≤ k −1 of or-

thogonal contrasts. Of particular interest are orthogonal contrasts sensitive

to polynomial trends among the ordered and equally spaced levels of a factor.

The requirement is that the design is balanced. For example, if k

=4,

Equispaced levels

Contrast 1 2 3 4

Linear

–3 –1 1 3

Quadratic

1 –1 –1 1

Cubic

–1 3 –1 3

11.2.3.2 Pairwise Comparisons

After rejecting H

, an assessment of H

can be conducted by pairwise compar-

isons. As the name suggests, this is a series of tests for all pairs of means in k

populations. Of course, there are

k(k−1)

different tests.

A common error in doing pairwise comparisons is to perform

(

−

two-

sample t-tests. The tests are dependent and the signiﬁcance level

α for simul-

taneous comparisons is difﬁcult to control. This is equivalent in spirit to si-

multaneously testing multiple hypotheses and adjusting the signiﬁcance level

of each test to control overall signiﬁcance level (p. 342). For example, for k

=5,

the Bonferroni procedure will require

α = 0.005 for individual comparisons in

order to control the overall signiﬁcance level at 0.05, clearly a conservative

approach.

Tukey (1952, unpubl. IMS address; 1953, unpubl. mimeograph) proposed a

test designed speciﬁcally for pairwise comparisons sometimes called the “hon-

estly signiﬁcant difference test.” The Tukey method is based on the so-called

studentized range distribution with quantiles q. The quantile used in a test

or a conﬁdence interval is q

ν,k,1−α

, with α being the overall signiﬁcance level

(or (1

−α)100% overall conﬁdence), k the number of treatments, and ν the er-

ror degrees of freedom, N

−k. The difference between two means µ

and µ

signiﬁcant if

− y

|> q

ν,k,1−α

, (11.3)

420 11 ANOVA and Elements of Experimental Design

where s =

MSE and n is the treatment sample size for a balanced

design. If the design is not balanced, then replace n in (11.3) by the har-

monic mean of n

s, n

1/n

(Tukey–Kramer procedure).

The function

qtukey(v,k,p) (Trujillo-Ortiz and Hernandez-Walls, MAT-

LAB Central #3469) approximates Tukey’s quantiles for inputs v

= N −k, k,

and p

=1 −α.

In biomedical experiments it is often the case that one treatment is consid-

ered a control and the only comparisons of interest are pairwise comparisons

of all treatments with the control, forming a total of k

−1 comparisons. This is

sometimes called the many-to-one procedure and it was developed by Dunnett

(1955).

Let

be the control mean. Then for i = 2, ..., k the mean µ

is different

than

− y

|> d

ν,k−1,α

1/n

+1/n

where

α is a joint signiﬁcance test for k−1 tests, and ν = N−k. The critical val-

ues d

ν,k−1,α

are available from the table at http://springer.bme.gatech.

edu/dunnett.pdf

It is recommended that the control treatment have more observations than

other treatments. A discussion on the sample size necessary to perform Dun-

nett’s comparisons can be found in Liu (1997).

Example 11.3. In the context of Example 11.1 (Coagulation Times), let us

compare the means using the Tukey procedure. This is a default for MAT-

LAB’s command

multcompare applied on the output stats in [p, table, stats]

= anova1(times, diets)

. The multcompare command produces an interactive

visual position for all means with their error bars and additionally gives an

output with a conﬁdence interval for each pair. If the conﬁdence interval con-

tains 0, then the means are not statistically different, according to Tukey’s

procedure. For example, the 95% Tukey conﬁdence interval for

−µ

[

−5.8241,1.8241], and the means µ

and µ

are “statistically the same.” On

the other hand, Tukey’s 95% interval for

−µ

is [−11.2754,−2.7246], indi-

cating that

is signiﬁcantly smaller than µ

multcompare(stats) %[p,table,stats] = anova1(times, diets)

%Compares means: 1-2; 1-3; 1-4; 2-3; 2-4; 3-4

%ans =

% 1.0000 2.0000 -9.2754 -5.0000 -0.7246

% 1.0000 3.0000 -11.2754 -7.0000 -2.7246

% 1.0000 4.0000 -4.0560 0 4.0560

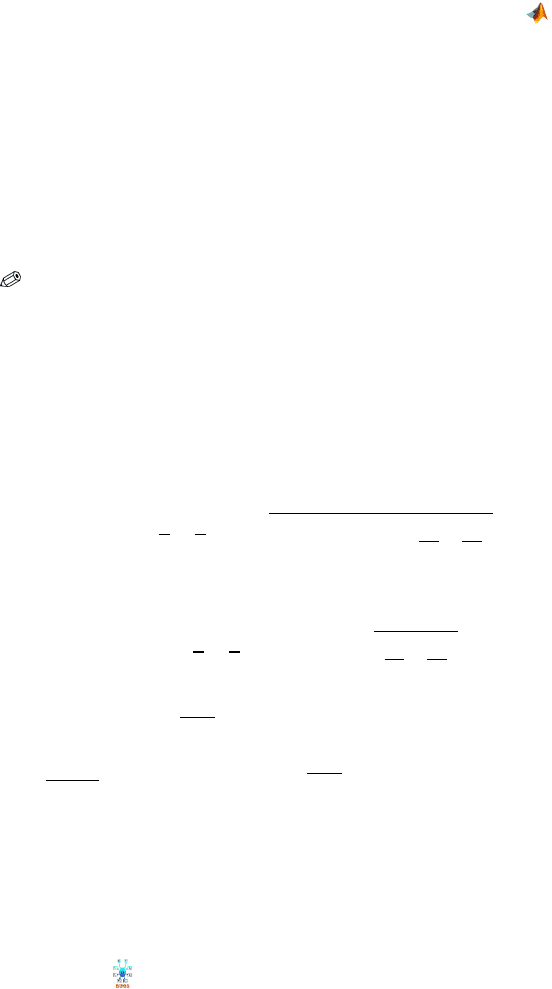
11.2 One-Way ANOVA 421

% 2.0000 3.0000 -5.8241 -2.0000 1.8241

% 2.0000 4.0000 1.4229 5.0000 8.5771

% 3.0000 4.0000 3.4229 7.0000 10.5771

We can also ﬁnd the Tukey’s conﬁdence intervals by using qtukey.m. For

example, the 95% conﬁdence interval for

−µ

m=stats.means;

%1-2

[m(1)-m(2) - qtukey(20,4,0.95)

stats.s

sqrt(1/2

(1/4+1/6)) ...

m(1)-m(2) ...

m(1)-m(2) + qtukey(20,4,0.95)

stats.s

sqrt(1/2

(1/4+1/6))]

% -9.3152 -5.0000 -0.6848

% Compare to: -9.2754 -5.0000 -0.7246 from multcompare

Although close to the output of multcompare, this interval differs due to a

coarser approximation algorithm in

qtukey.m.



In addition to Tukey and Dunnett, there is a range of other multiple com-

parison procedures. For example, Bonferroni is easy but too conservative.

Since there are

pairs among k means, replacing α by α

∗

=α/

would con-

trol all the comparisons at level

α. Scheffee’s multiple comparison procedure

provides a simultaneous 1

−α-level conﬁdence interval for all linear combi-

nations of population means and as a special case all pairwise differences.

Scheffee’s (1

−α)100% conﬁdence interval for µ

−µ

is given by

− y

|±s

(k −1)F

α,k−1,n−k

Sidak’s multiple comparison conﬁdence intervals are

− y

|±t

n−k,α

∗

where

∗

=1−(1−α)

k(k−1)

. Note that Sidak’s comparisons are just slightly less

conservative than Bonferroni’s for which the

∗

= α/

. Since (1 −α)

= 1 −

mα+

(

−

−..., Sidak’s 1−(1−α)

k(k−1)

is approx. α/

, which is Bonferroni’s

choice.

11.2.4 Bayesian Solution

Next we provide a Bayesian solution for the same problem. In the Win-

BUGS code (

anovacoagulation.odc) we stipulate that the data are normal

with means equal to the grand mean, plus the effect of diet,

mu[i]<-mu0 +

422 11 ANOVA and Elements of Experimental Design

alpha[diets[i]]. The priors on alpha[i] are noninformative and depend on

the selection of identiﬁability constraint. Here the code uses sum-to-zero, a

STZ constraint that ﬁxes one of the

αs, while the rest are given standard non-

informative priors for the location. For example,

is ﬁxed as −(α

+···+α

which explains the term sum-to-zero. Another type of constraints that ensures

model identiﬁability is corner or CR constraint. In this case “corner” value

is set to 0. Then the treatment 1 is considered as a baseline category.

The grand mean

mu0 is given a noninformative prior as well.

The parameter

tau is a precision, that is, a reciprocal of variance. Tradi-

tionally, the noninformative prior on the precision is gamma with small pa-

rameters, in this case

dgamma(0.001,0.001). From tau, the standard deviation

is calculated as

sigma<-sqrt(1/tau). Thus, the highlights of the code are (i)

the indexing of alpha via

diets[i], (ii) the identiﬁability constraints, and (iii)

the choice of noninformative priors.

model{

for (i in 1:ntotal){

times[i] ~ dnorm( mu[i], tau )

mu[i] <- mu0 + alpha[diets[i]]

}

#alpha[1] <- 0.0; #CR Constraint

alpha[1] <- -sum( alpha[2:a] ); #STZ Constraint

mu0 ~ dnorm(0, 0.0001)

alpha[2] ~ dnorm(0, 0.0001)

alpha[3] ~ dnorm(0, 0.0001)

alpha[4] ~ dnorm(0, 0.0001)

tau ~ dgamma(0.001, 0.001)

sigma <- sqrt(1/tau)

}

DATA

list(ntotal = 24, a=4,

times =c(62, 60, 63, 59, 63, 67, 71, 64, 65, 66,

68, 66, 71, 67, 68, 68, 56, 62, 60, 61, 63, 64, 63, 59),

diets = c(1,1,1,1, 2,2,2,2,2,2, 3,3,3,3,3,3, 4,4,4,4,4,4,4,4) )

INITS

list( mu0=0, alpha = c(NA,0,0,0), tau=1)

mean sd MC error val2.5pc median val97.5pc start sample

alpha[1] –3.001 1.03 0.002663 –5.039 –3.002 –0.9566 1001 100000

alpha[2] 1.999 0.893 0.003573 0.2318 1.999 3.774 1001 100000

alpha[3] 4.001 0.8935 0.003453 2.232 4.002 5.779 1001 100000

alpha[4] –2.999 0.8178 0.003239 –4.61 –2.999 –1.382 1001 100000

mu0 64.0 0.5248 0.00176 62.96 64.0 65.03 1001 100000

sigma 2.462 0.4121 0.001717 1.813 2.408 3.422 1001 100000

tau 0.1783 0.05631 2.312E-4 0.08539 0.1724 0.3043 1001 100000

11.2 One-Way ANOVA 423

Figure 11.2a summarizes the posteriors of treatment effects, α

,... , α

as boxplots. Once the simulation for ANOVA is completed in WinBUGS, this

graphical output becomes available under

Inference>Compare tab.

(a) (b)

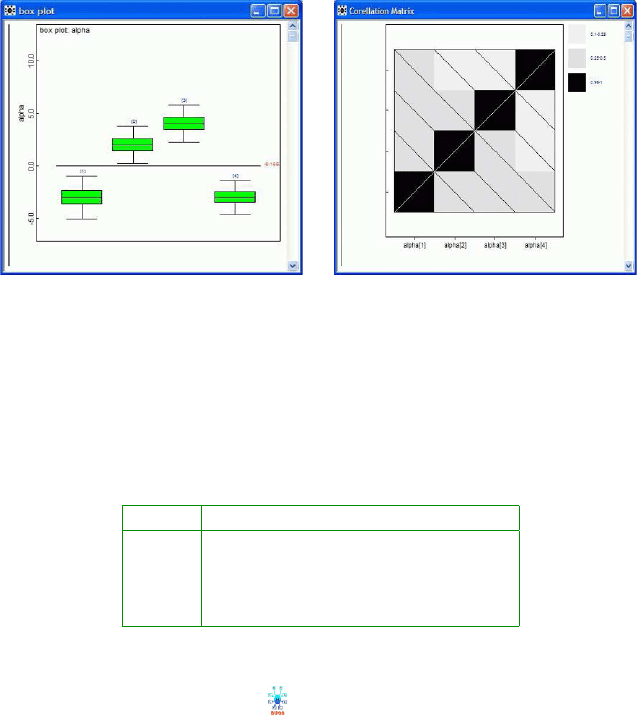
Fig. 11.2 (a) WinBUGS output from

Inference>Compare. Boxplots of posterior realiza-

tions of treatment effects

alpha. (b) Matrix of correlations among components of alpha.

WinBUGS can also estimate the correlations between the treatment ef-

fects. The correlation matrix below and its graphical representation (Fig. 11.2b)

are outputs from

Inference>Correlations.

alpha[1] alpha[2] alpha[3] alpha[4]

alpha[1] 1.0 –0.4095 –0.4056 –0.3694

alpha[2] –0.4095 1.0 –0.3059 –0.2418

alpha[3] –0.4056 –0.3059 1.0 –0.2476

alpha[4] –0.3694 –0.2418 –0.2476 1.0

Note that off-diagonal correlations are negative, as expected because of

STZ constraint.

Expand the WinBUGS code

anovacoagulation.odc to accommodate the

six differences

diff12 <- alpha[1]-alpha[2],. . . , diff34 <- alpha[3]-alpha[4].

Compare credible sets for the differences with MATLAB’s

multcompare output.

11.2.5 Fixed- and Random-Effect ANOVA

In Example 11.1 (Coagulation Times) the levels of the factor are ﬁxed: dietA,

..., dietD. Such ANOVAs are called ﬁxed-effect ANOVAs. Sometimes, the

number of factor levels is so large that a random subset is selected and serves

424 11 ANOVA and Elements of Experimental Design

as a set of levels. Then the inference is not concerned with these speciﬁc ran-

domly selected levels but with the population of levels. For example, in mea-

suring the response in animals to a particular chemical in food, a researcher

may believe that the type of animal may be a factor. He/she would select a ran-

dom but small number of different species as the levels of the factor. Inference

about this factor would be translated to all potential species. In measuring

the quality of healthcare, the researcher may have several randomly selected

cities in the USA as the levels of the factor. For such models, the effects

, i =

1,... , k are assumed normal N (0,σ

), and the ANOVA hypothesis is equiva-

lent to H

: σ

= 0. Thus, for the random-effect model, E(MSTr) = σ

+σ

, as

opposed to the ﬁxed-effect case,

E(MST r) =σ

k−1

If s

= MST r, then in random effect ANOVA the variance components are

estimated as:

= s

= MSE, and

−s

Thus testing H

: σ

= 0 is based on s

= MST r/MSE, which has an F-

distribution with k

−1, N −k degrees of freedom. Operationally, the random-

effect and ﬁxed-effect ANOVAs coincide, and the same ANOVA table can be

used. The two differ mostly in the interpretation of the inference and the

power analysis. Gauge R&R ANOVA in Sec. 11.10 is an example of a random-

effect ANOVA.

11.3 Two-Way ANOVA and Factorial Designs

Many experiments involve two or more factors. For each combination of factor

levels an experiment is performed and the response recorded. We will discuss

only factorial designs with two factors; the interested reader is directed to

Kutner et al. (2004) for a comprehensive treatment of multifactor designs and

incomplete factorial designs.

Denote the two factors by A and B and assume that factor A has a levels

and B has b levels. Then for each a

×b combination of levels we perform the

experiment n

≥ 1 times. Measurements at ﬁxed levels of A and B are called

replicates. Such a design will be called a factorial design. When factors are

arranged in a factorial design, they are called crossed. If the number of repli-

cates is the same for each cell (ﬁxed levels for A and B), then the design is

called balanced. We will be interested not only in how the factors inﬂuence the

response, but also if the factors interact.

Suppose that the responses y

i jk

are obtained under the ith level of factor A

and the jth level of factor B. For each cell (i, j) one obtains n

i j

replicates, and

i jk

is the kth replicate. The model for y

i jk

=µ +α

+β

+(αβ)

i j

+²

i jk

, i =1,.. . , a; j =1,..., b; k =1,..., n

i j

. (11.4)

11.3 Two-Way ANOVA and Factorial Designs 425

Thus, the observation y

i jk

is modeled as the grand mean µ, plus the inﬂuence

of factor A,

, plus the inﬂuence of factor B, β

, plus the interaction term

(

αβ)

i j

, and, ﬁnally, plus the random error ²

i jk

. As in the one-way ANOVA,

the errors

i jk

are assumed independent normal with zero mean and constant

variance

for all i, j, and k.

To ensure the identiﬁability of decomposition in (11.4) restrictions on

s, and (αβ)

i j

s need to be imposed. Standardly, it is assumed that

i=1

=0,

j=1

=0,

i=1

(αβ)

i, j

=0,

j=1

(αβ)

i, j

=0,

although different restrictions are possible, as we will see in the Bayesian

models.

In two-factor factorial design there are three hypotheses to be tested:

effects of factor A,

: α

=α

=···=α

=0 versus H

=(H

)

effects of factor B,

: β

=β

=···=β

=0 versus H

=(H

)

and the interaction of A and B,

000

: (αβ)

=(αβ)

=···=(αβ)

=0 versus H

000

=(H

000

)

The variability in observations follows the fundamental ANOVA identity

in which the total sum of squares (SST) is represented as a sum of the A-

treatment sum of squares (SSA), a sum of the B-treatment sum of squares

(SSB), the interaction sum of squares (SSAB), and the sum of squares due to

error (SSE). For a balanced design in which the number of replicates in all

cells is n,

SST

= SS A +SSB +SSAB +SSE

i=1

j= 1

k=1

i jk

− y

...

)

= bn

i=1

i..

− y...)

+an

j=1

. j.

− y

...

)

i=1

j=1

i j.

− y

i..

− y

. j.

+ y

...

)

i=1

j=1

k=1

i jk

− y

i j.

)

426 11 ANOVA and Elements of Experimental Design

Here,

...

abn

i=1

j=1

k=1

i jk

, y

i..

j=1

k=1

i jk

. j.

i=1

k=1

i jk

, and y

i j.

k=1

i jk

The point estimator for

effects is

= y

i..

− y

...

, for β

effects it is

= y

. j.

−

...

, and for the interaction (αβ)

i j

it is



(αβ)

i j

= y

i j.

− y

i..

− y

. j.

+ y

...

The degrees of freedom are partitioned according to the ANOVA identity as

abn

−1 =(a−1)+(b−1)+(a− 1)(b−1)+ab(n−1). Outputs in standard statistical

packages include degrees of freedom (DF), mean sum of squares, F-ratios and

their p-values.

Source DF SS MS F p-value

Factor A a −1 SS A MS A =

SSA

a−1

MS A

MSE

P(F

a−1,ab(n−1)

)

Factor B b

−1 SSB MSB =

SSB

b−1

MSB

MSE

P(F

b−1,ab(n−1)

)

× B (a −1)(b −1) SS AB MS AB =

SSAB

(a−1)(b−1)

MS AB

MSE

P(F

(a−1)(b−1),ab(n−1)

)

Error ab(n

−1) SSE MSE =

SSE

ab(n−1)

Total abn −1 SST

, F

, and F

are test statistics for H

, H

, and H

000

, and their large

values are critical. The rationale for these tests follows from the following

expected values:

E(MSE) =σ

, E(MS A) =σ

a −1

i=1

, E(MSB) = σ

b −1

j=1

, and

E(MS AB) =σ

(a −1)(b −1)

i=1

j=1

(αβ)

i j

Example 11.4. Insulin Therapy. Insulin has anti-inﬂammatory effects, as

evaluated by its ability to reduce plasma concentrations of cytokines. The cy-

tokine content in several organs after endotoxin (lipopolysaccharide, LPS) ex-

posure and the effect of hyperinsulinaemia was examined in a porcine model

(Brix-Christensen et al., 2005). All animals (35 to 40 kg) were subject to gen-

eral anaesthesia and ventilated for 570 minutes. There were two possible in-

terventions:

LPS: Lipopolysaccharide infusion for 180 minutes.

HEC: Hyperinsulinemic euglycemic clamp in 570 minutes (from start). In-

sulin was infused at a constant rate and plasma glucose was clamped at a

certain level by infusion of glucose.

11.3 Two-Way ANOVA and Factorial Designs 427

LPS induces a systemic inﬂammation (makes the animals sick) and HEC

acts as a treatment. There were four experimental cells: (1) only anaesthesia

(no HEC, no LPS), (2) HEC, (3) LPS, and (4) HEC and LPS.

The responses are levels of interleukin-10 (IL-10) in the kidney after

330 minutes have elapsed. The table corresponds to a balanced design n

= 8,

although the original experiment was unbalanced with ten animals in group 1,

nine in group 2, ten in group 3, and nine in group 4.

No HEC Yes HEC

7.0607 4.7510 3.0693 2.1102

No LPS 2.6168 2.9530 1.6489 3.1004

4.3489 3.6137 2.9160 4.1170

3.6356 5.6969 2.9149 3.0229

3.6911 4.5554 2.4159 1.8944

4.3933 3.8447 3.1493 3.5133

Yes LPS 6.0513 1.3590 4.4462 4.6254

4.2559 2.1449 2.8545 3.8967

%insulin.m

data2 = [... %columns: IL10 LPS HEC

7.0607 1 1; 2.6168 1 1; 4.3489 1 1;...

3.6356 1 1; 4.7510 1 1; 2.9530 1 1;...

3.6137 1 1; 5.6969 1 1; 3.0693 1 2;...

1.6489 1 2; 2.9160 1 2; 2.9149 1 2;...

2.1102 1 2; 3.1004 1 2; 4.1170 1 2;...

3.0229 1 2; 3.6911 2 1; 4.3933 2 1;...

6.0513 2 1; 4.2559 2 1; 4.5554 2 1;...

3.8447 2 1; 1.3590 2 1; 2.1449 2 1;...

2.4159 2 2; 3.1493 2 2; 4.4462 2 2;...

2.8545 2 2; 1.8944 2 2; 3.5133 2 2;...

4.6254 2 2; 3.8967 2 2];

IL10 = data2(:,1); LPS=data2(:,2); HEC=data2(:,3);

[p table stats terms] = anovan( IL10, {LPS,HEC}, ...

’varnames’,{’LPS’,’HEC’}, ’model’,’interaction’)

The resulting ANOVA table provides the test for the two factors and their

interaction.

Source DF SS MS F p-value

LPS 1 0.0073 0.0073 0.0051 0.9436

HEC 1 7.2932 7.2932 5.0532 0.0326

LPS*HEC 1 2.1409 2.1409 1.4834 0.2334

Error 28 40.4124 1.4433

Total 31 49.8539

Note that factor LPS is insigniﬁcant. The associated F statistic is 0.0051

with p-value of 0.9436. The interaction (LPS*HEC) is insigniﬁcant as well

(p-value of 0.2334), while HEC is signiﬁcant (p-value of 0.0326).

428 11 ANOVA and Elements of Experimental Design

Next, we generate the interaction plots.

%insulin.m continued

cell11 = mean(data2( 1: 8,1)) %L1 H1

cell12 = mean(data2( 9:16,1)) %L1 H2

cell21 = mean(data2(17:24,1)) %L2 H1

cell22 = mean(data2(25:32,1)) %L2 H2

figure;

plot([1 2],[cell11 cell12],’o’,’markersize’,10, ...

’MarkerEdgeColor’,’k’,’MarkerFaceColor’,’r’)

hold on

plot([1 2],[cell11 cell12],’r-’, ’linewidth’,3)

plot([1 2],[cell21 cell22],’o’,’markersize’,10, ...

’MarkerEdgeColor’,’k’,’MarkerFaceColor’,’k’)

plot([1 2],[cell21 cell22],’k-’, ’linewidth’,3)

title(’Lines for LPS=1 (red) and LPS = 2 (black)’)

xlabel(’HEC’)

figure;

plot([1 2],[cell11 cell21],’o’,’markersize’,10, ...

’MarkerEdgeColor’,’k’,’MarkerFaceColor’,’r’)

hold on

plot([1 2],[cell11 cell21],’r-’,’linewidth’,3)

plot([1 2],[cell12 cell22],’o’,’markersize’,10, ...

’MarkerEdgeColor’,’k’,’MarkerFaceColor’,’k’)

plot([1 2],[cell12 cell22],’k-’,’linewidth’,3)

title(’Lines for HEC=1 (red) and HEC = 2 (black)’)

xlabel(’LPS’)

1 1.2 1.4 1.6 1.8 2

0.5

1.5

2.5

3.5

4.5

Lines for LPS=1 (red) and LPS = 2 (black)

HEC

1 1.2 1.4 1.6 1.8 2

0.5

1.5

2.5

3.5

4.5

Lines for HEC=1 (red) and HEC = 2 (black)

LPS

(a) (b)

Fig. 11.3 Interaction plots of LPS against HEC (left) and HEC against LPS (right) to explore

the additivity of the model.

Figure 11.3 presents treatment mean plots, also known as interaction

plots. The x-axis contains the levels of the factors, in this case both factors