Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

7.2 Moment Matching and Maximum Likelihood Estimators 237

Example 7.5. Suppose the observations X

= 2, X

= 5, X

= 0.5, and X

= 3

come from the uniform

U (0, θ) distribution. We are interested in estimating

θ. The density for the single observation X is f (x|θ) =

1(0 ≤ x ≤ θ), and the

likelihood, based on n observations X

,... , X

, is

θ|X

,... , X

) =

·1(0 ≤ X

≤θ) ·1(0 ≤ X

≤θ) · . . . ·1(0 ≤ X

≤θ).

The product in the above expression can be simpliﬁed: if all X s are less than

or equal to

θ, then their maximum X

(n)

is less than θ as well. Thus,

1(0 ≤ X

≤θ) ·1(0 ≤ X

≤θ) · . . . ·1(0 ≤ X

≤θ) = 1(X

(n)

≤θ).

Maximizing the likelihood now can be performed by inspection. In order to

maximize

, subject to X

(n)

≤θ, one should take the smallest θ possible, and

that

θ is X

(n)

= max X

. Therefore,

mle

= X

(n)

, and in this problem, the esti-

mator is X

(4)

= X

=5.

An alternative estimator can be found by moment matching. One can show

(the arguments are beyond the scope of this book) that in estimating

θ in

U (0, θ), only max X

should be used. What is the distribution of max X

We will ﬁnd this distribution for general i.i.d. X

, i =1,... , n, with CDF F(x)

and PDF f (x)

(x).

The CDF is, by deﬁnition,

G(x)

=P(max X

≤ x) =P(X

≤ x, X

≤ x,. . ., X

≤ x) =

i=1

P(X

≤ x) =(F(x))

The reasoning in the above equation is as follows. If the maximum is

≤

then all X

are ≤ x, and vice versa. The density for max X

is g(x) = G

(x) =

n F

n−1

(x) f (x), and the ﬁrst moment is

E max X

x g(x) dx =

x n F

n−1

(x) f (x) dx.

For the uniform distribution

U (0, θ),

E max X

x ·n (x/θ)

n−1

·1/θ dx =

dx =

n +1

θ.

The expectation of the maximum

E max X

is matched with the largest order

statistic in the sample, X

(n)

. Thus, by solving the moment-matching equation,

one obtains an alternative estimator for

θ,

n+1

(n)

. In this problem,

=25/4 =6.25. For a Bayesian estimator, see Example 8.6.

238 7 Point and Interval Estimators

7.2.1 Unbiasedness and Consistency of Estimators

Based on a sample X

,... , X

from a population with distribution f (x|θ), let

= g(X

,... , X

) be a statistic that estimates the parameter θ. The statistic

(estimator)

as a function of the sample is a random variable. As a random

variable, the estimator would have an expectation of

, a variance of Var

and its own distribution called a sampling distribution.

Example 7.6. Suppose we are interested in ﬁnding the proportion of subjects

with the AB blood group in a particular geographic region. This proportion,

θ, is to be estimated on the basis of the sample Y

,... , Y

, each having a

Bernoulli

B er(θ) distribution taking values 1 and 0 with probabilities θ and

−θ, respectively. The realization Y

=1 indicates the presence of the AB group

in observation i. The sum X

is by deﬁnition binomial B in(n,θ).

The estimator for

θ is

=Y =

. It is easy to check that this estimator is

both moment matching (

=θ) and MLE (the likelihood is θ

(1−θ)

n−

Thus

has a binomial distribution with rescaled realizations {0, 1/n, 2/n,...,

−1)/n, 1}, that is,

(1 −θ)

n−k

, k =0,1,..., n,

which is the estimator’s sampling distribution.

It easy to show, by referring to a binomial distribution, that the expectation

is 1/n times the expectation of the binomial, nθ,

×nθ =θ,

and that the variance is

Var

×nθ(1 −θ) =

θ(1−θ)

If E

= θ, then the estimator

θ is called unbiased. The expectation is

taken with respect to the sampling distribution. The quantity

θ) =E

−θ

is called the bias of

θ.

The error in estimation can be assessed by various measures. The most

common is the mean squared error (MSE).

7.2 Moment Matching and Maximum Likelihood Estimators 239

The MSE is deﬁned as

MSE(

θ,θ) =E(

−θ)

The MSE represents the expected squared deviation of the estimator from

the parameter it estimates. This expectation is taken with respect to the sam-

pling distribution of

From the deﬁnition of MSE,

−θ)

= E(

−E

−θ)

= E(

−E

)

−2E(

−E

)(E

−θ) +(E

−θ)

= E(

−E

)

+(E

−θ)

Consequently, the MSE can be represented as a sum of the variance of the

estimator and its bias squared:

MSE(

θ,θ) =Var

θ +b(θ)

The square root of the MSE is sometimes used; it is called the root mean

squared error (RMSE). For example, in estimating the population proportion,

the estimator

= X /n, for the X ∼B in(n, p) model, is unbiased, E(

p) = p. Then

the MSE is

Var (

p) = pq/n, and the RMSE is

pq/n. Note that the RMSE is a

function of the parameter. If parameter p is replaced by its estimator

p, then

the RMSE becomes the standard error, s.e., of the estimator. For binomial p,

the standard error of

p is s.e.(

q/n.

Remark. The standard error (s.e.) of any estimator usually refers to a

sample counterpart of its RMSE (sample counterpart of standard deviation

for unbiased estimators). For example, if X

, X

,... , X

are N (µ, σ

), then

s.e.(

X ) = s/

Inspecting the variance (when the sample size increases) of an unbiased

estimator allows for checking its consistency. The consistency property is a

desirable property of estimators. Informally, it is deﬁned as the convergence of

an estimator (in a stochastic sense) to the parameter it estimates.

If, for an unbiased estimator

, Var

→0 when the sample size n →∞,

the estimator is called consistent.

240 7 Point and Interval Estimators

More advanced deﬁnitions of convergences of random variables, which are

beyond the scope of this text, are required in order to deduce more precise def-

initions of asymptotic unbiasedness and weak and strong consistency; there-

fore, these deﬁnitions will not be discussed here.

Example 7.7. Suppose that we are interested in estimating the parameter

in a population with a distribution of N (0,θ),θ > 0, and that the proposed

estimator, when the sample X

, X

,... , X

is observed, is

θ =

It is easy to demonstrate that, when X

∼ N (0,θ), EX

= θ and EX

= 3θ

by representing X as

θZ for Z ∼N (0,1) and using the fact that EZ

=1 and

=3.

The estimator

θ =

= X

is unbiased and consistent. Since E

θ =

nθ = θ, the estimator is unbiased. To show consistency, it is

sufﬁcient to demonstrate that the variance tends to 0 as the sample size in-

creases. This is evident from

Var

θ =

i=1

Var X

3nθ

3θ

→0, when n →∞.

Alternatively, one may use the fact that

has a χ

distribution, so

that the sampling distribution of

θ is a scaled χ

, where the scaling factor is

nθ

. The unbiasedness and consistency follow from Eχ

= n and Var χ

=2n by

accounting for the scaling factor.

Some important examples of unbiased and consistent estimators are pro-

vided next.

7.3 Estimation of a Mean, Variance, and Proportion

7.3.1 Point Estimation of Mean

For a sample X

,... , X

of size n we have already discussed the sample mean

X =

as an estimator of location. A natural estimator of the popu-

lation mean

µ is the sample mean

µ = X . The estimator X is an “optimal”

estimator of a mean in many different models/distributions and for many dif-

ferent deﬁnitions of optimality.

The estimator

X varies from sample to sample. More precisely, X is a ran-

dom variable with a ﬁxed distribution depending on the common distribution

of observations, X

7.3 Estimation of a Mean, Variance, and Proportion 241

The following is true for any distribution in the population as long as

=µ and Var (X

) =σ

exist:

EX =µ, Var (X ) =

. (7.2)

The above equations are a direct consequence of independence in a sample

and imply that

X is an unbiased and consistent estimator of µ.

If, in addition, we assume normality X

∼N (µ,σ

), then the sampling dis-

tribution of

X is known exactly,

X ∼N

µ,

and the relations in (7.2) are apparent.

Chebyshev’s Inequality and Strong Law of Large Numbers*. There

are two general results in probability that theoretically justify the use of the

sample mean

X to estimate the population mean, µ. These are Chebyshev’s

inequality and strong law of large numbers (SLLN). We will discuss these

results without mathematical rigor.

The Chebyshev inequality states that when X

, X

,... , X

are i.i.d. ran-

dom variables with mean

µ and ﬁnite variance σ

, the probability that X will

deviate from

µ is small,

P(|X

−µ|≥²) ≤

n²

for any

² > 0. The inequality is a direct consequence of (5.8) with (X

−µ)

place of X and

in place of a.

To translate this to speciﬁc numbers, choose

² small, say 0.000001. Assume

that the X

s have a variance of 1. The Chebyshev inequality states that with

n larger than the solution of 1/(n

×0.0000001

) =0.9999, the distance between

and µ will be smaller than 0.000001 with a probability of 99.99%. Admit-

tedly, n here is an experimentally unfeasible number; however, for any small

², ﬁnite σ

, and “conﬁdence” close to 1, such n is ﬁnite.

The laws of large numbers state that, as a numerical sequence,

con-

verges to

µ. Care is needed here. The sequence X

is not a sequence of num-

bers but a sequence of random variables, which are functions deﬁned on sam-

ple spaces

S . Thus, direct application of a “calculus” type of convergence is

not appropriate. However, for any ﬁxed realization from sample space

S , the

sequence

becomes numerical and a traditional convergence can be stated.

Thus, a correct statement for the so-called SLLN is

242 7 Point and Interval Estimators

P(X

→µ) =1,

that is, conceived as an event,

→µ

is a sure event – it happens with a

probability of 1.

7.3.2 Point Estimation of Variance

We will obtain an intuition starting, once again, with a ﬁnite population:

,... , y

. The population variance is σ

−µ)

, where µ =

is the population mean.

If a sample X

, X

,... , X

is observed, an estimator of σ

i=1

−µ)

for

µ known, or

= s

n −1

i=1

−X )

for

µ not known and estimated by X .

In the expression for s

we divide by n −1 instead of the “expected” n in

order to ensure the unbiasedness of s

, Es

=σ

. The proof is easy and does not

require any distributional assumptions, except that the population variance

is ﬁnite.

Note that by the deﬁnition of variance,

E(X

−µ)

=σ

and E(X −µ)

=σ

/n.

−1)s

i=1

−X )

i=1

[(X

−µ) −(X −µ)]

i=1

−µ)

−2n(X −µ)

i−1

−µ) +n(X −µ)

i=1

−µ)

−n(X −µ)

, since

i=1

−µ) = n(X −µ).

Then,

7.3 Estimation of a Mean, Variance, and Proportion 243

E(s

) =

n −1

E(n −1)s

n −1

i=1

−µ)

−n(X −µ)

]

n −1

−n

)

n −1

−1)σ

=σ

When, in addition, the population is normal

N (µ,σ

), then

(n −1)s

∼χ

−1

i.e., the statistic

(n−1)s

−X

has a χ

distribution with n−1 degrees

of freedom (see Eq. 6.3 and related discussion).

For a sample from a normal distribution, unbiasedness of s

is an easy con-

sequence of the representation s

∼

n−1

−1

and Eχ

−1

=(n −1). The variance

of s

Var s

n −1

×Var χ

−1

2σ

n −1

(7.3)

since

Var χ

−1

=2(n−1). Unlike the unbiasedness result, Es

=σ

, which does

not require a normality assumption, the result in (7.3) is valid only when ob-

servations come from a normal distribution.

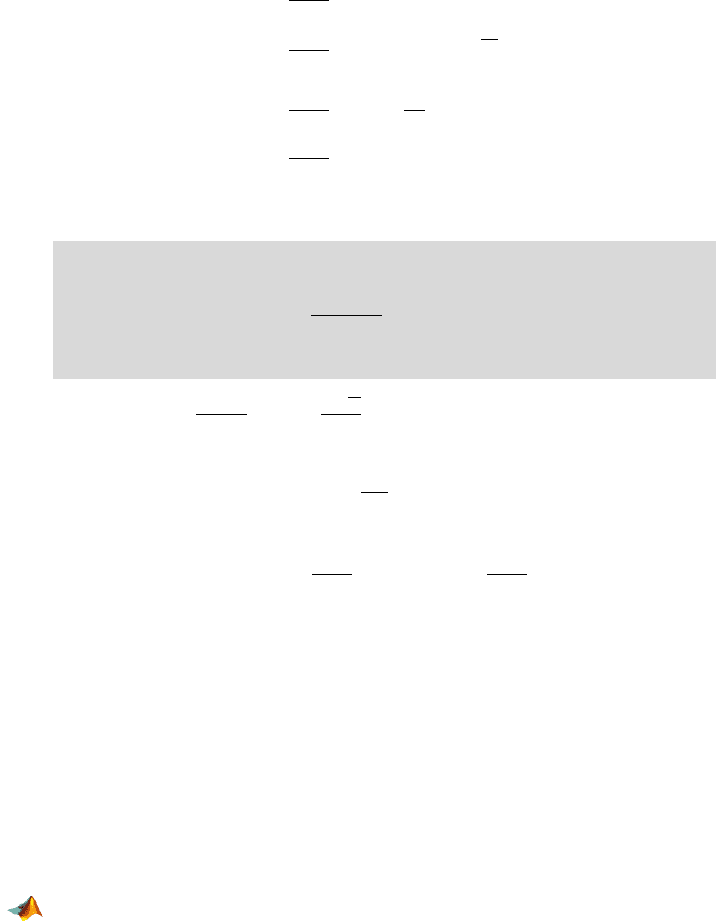
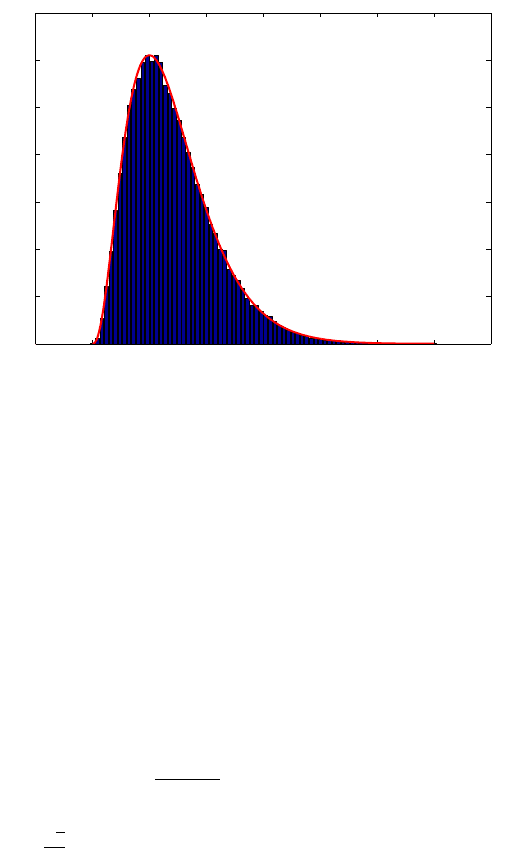
Figure 7.3 indicates that the empirical distribution of normalized sample

variances is close to a

distribution. We generated M = 100000 samples of

size n

=8 from a normal N (0,5

) distribution and found sample variances s

for each sample. The sample variances are multiplied by n −1 =7 and divided

=25. The histogram of such rescaled sample variances is plotted and the

density of a

distribution with 7 degrees of freedom is superimposed in red.

The code generating Fig. 7.3 is given next.

M=100000; n = 8;

X = 5

randn([n, M]);

ch2 = (n-1)

var(X)/25;

histn(ch2,0,0.4,30)

hold on

plot( (0:0.1:30), chi2pdf((0:0.1:30), n-1),’r-’)

244 7 Point and Interval Estimators

−5 0 5 10 15 20 25 30 35

0.02

0.04

0.06

0.08

0.1

0.12

0.14

Fig. 7.3 Histogram of normalized sample variances (n −1)s

/σ

obtained from M =100000

independent samples from

N (0, 5

), each of size n =8. The density of a χ

distribution with

7 degrees of freedom is superimposed in red.

The code is quite efﬁcient since a for-end loop is avoided. The simulated

object

X is an n ×M matrix consisting of M columns (samples) of length n. The

operator

var(X) acts on columns of X producing M sample variances.

Several Robust Estimators of the Standard Deviation*. Suppose

that a sample X

,... , X

is observed and normality is not assumed. We dis-

cuss two estimators of the standard deviation that are calibrated by the nor-

mal distribution but quite robust with respect to outliers and deviations from

normality.



Gini’s mean difference is deﬁned as

n(n −1)

1≤i<j≤n

−X

The statistic G

is an estimator of the standard deviation and is more robust

to outliers than the standard statistic s.

Another proposal by Croux and Rousseeuw (1992) involves absolute differ-

ences as in Gini’s mean difference estimator but uses kth-order statistic rather

than the average. The estimator of

σ is

=2.2219 {|X

−X

|, i < j}

(k)

, where k =

n/2c+1

7.3 Estimation of a Mean, Variance, and Proportion 245

The constant 2.2219 is needed for the calibration of the estimator, so that if the

sample is a standard normal, then Q

= 1. In calculating Q, all

differences

−X

| are ordered, and the kth in rank is selected and multiplied by 2.2219.

This choice of k requires an additional multiplicative correction factor n/(n

1.4) for n odd, or n/(n +3.8) for n even.

MATLAB scripts

ginimd.m and crouxrouss.m evaluate the estimator.

The algorithm is naïve and uses a double loop to evaluate G and Q. The

evaluation breaks down for sample sizes of less than 500 because of memory

problems. A smarter algorithm that avoids looping is implemented in versions

ginimd2.m and crouxrouss2.m. In these versions, the sample size can go up to

6000.

In the following MATLAB session we demonstrate the performance of ro-

bust estimators of the standard deviation. If 1000 standard normal random

variates are generated and one value is replaced with a clear outlier, say

1000

= 20, we will explore the inﬂuence of this outlier to estimators of the

standard deviation. Note that s is quite sensitive and the outlier inﬂates the

estimator by almost 20%. The robust estimators are affected as well, but not

as much as s.

x =randn(1, 1000);

x(1000)=20;

std(x)

% ans = 1.1999

s1 = ginimd2(x)

%s1 =1.0555

s2 = crouxrouss2(x)

%s2 =1.0287

iqr(x)/1.349

%ans = 1.0172

There are many other robust estimators of the variance/standard devia-

tion. Good references containing extensive material on robust estimation are

Wilcox (2005) and Staudte and Sheater (1990).

7.3.3 Point Estimation of Population Proportion

It is natural to estimate the population proportion p by a sample proportion.

The sample proportion is the MLE and moment-matching estimator for p.

Sample proportions use a binomial distribution as the theoretical model.

Let X

∼B in(n, p), where parameter p is unknown. The MLE of p based on a

single observation X is obtained by maximizing the likelihood

(1 − p)

n−X

246 7 Point and Interval Estimators

or the log-likelihood

factor free of p

+X log(p)+(n −X ) log(1 − p).

The maximum is obtained by solving

(factor free of p

+X log(p)+(n −X ) log(1 − p))

−

n −X

1 − p

=0,

which after some algebra gives the solution

mle

In Example 7.6 we argued that the exact distribution for X /n is a rescaled

binomial and that the statistic is unbiased, with the variance converging to

0 when the sample size increases. These two properties deﬁne a consistent

estimator.

7.4 Conﬁdence Intervals

Whenever the sampling distribution of a point estimator

is continuous, then

necessarily

= θ) = 0. In other words, the probability that the estimator

exactly matches the parameter it estimates is 0.

Instead of the point estimator, one may report two estimators, L

= L(X

,... ,

) and U = U(X

,... , X

), so that the interval [L,U] covers θ with a proba-

bility of 1

−α, for small α. In this case, the interval [L,U] will be called a

−α)100% conﬁdence interval for θ.

For the construction of a conﬁdence interval for a parameter, one needs to

know the sampling distribution of the associated point estimator. The lower

and upper interval bounds L and U depend on the quantiles of this distribu-

tion. We will derive the conﬁdence interval for the normal mean, normal vari-

ance, population proportion, and Poisson rate. Many other conﬁdence inter-

vals, including differences, ratios, and some functions of statistics, are tightly

connected to testing methodology and will be discussed in subsequent chap-

ters.

Note that when the population is normal and X

,... , X

is observed, the

exact sampling distributions of

X −µ

σ/

and

X −µ

σ/

(n−1)s

/(n −1)