Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

6.6 Distributions Related to Normal 217

ncx2cdf, ncx2inv, ncx2stat, and ncx2rnd for PDF, CDF, quantile, descriptive

statistics, and random number generator.

Random variable t

n,δ

has a noncentral t distribution with n degrees of free-

dom and noncentrality parameter

δ if it can be represented as

n,δ

where X and

are independent, X ∼ N (δ,1), and χ

has a (central) χ

dis-

tribution with n degrees of freedom. In MATLAB, functions

nctpdf, nctcdf,

nctinv, nctstat, and nctrnd, stand for PDF, CDF, quantile, descriptive statis-

tics, and random number generator of the noncentral t.

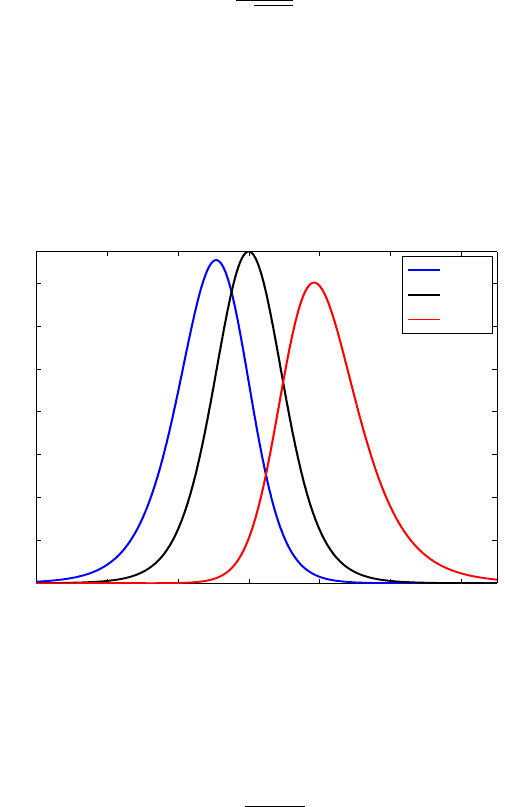
Figure 6.14 plots the densities of noncentral t for values of the noncentral-

ity parameter

−1,0, and 2. Noncentral t for δ =0 is a standard t distribution.

−6 −4 −2 0 2 4 6

0.05

0.1

0.15

0.2

0.25

0.3

0.35

nct

8,−1

nct

8,2

Fig. 6.14 Densities of noncentral t

8,δ

distribution for δ =−1,0,2

Random variable F

m,n,δ

has a noncentral F-distribution with m, n degrees

of freedom and parameter of noncentrality

δ if it can be represented as

m,n,δ

where

and χ

are independent, with noncentral (δ) and standard χ

dis-

tributions with m and n degrees of freedom, respectively. In MATLAB, func-

tions

ncfpdf, ncfcdf, ncfinv, ncfstat, and ncfrnd, stand for the PDF, CDF,

218 6 Normal Distribution

quantile, descriptive statistics, and random number generator of the noncen-

tral F.

The noncentral F will be used in Chap. 11 for power calculations in several

ANOVA designs.

6.6.6 Lognormal Distribution

A random variable X has a lognormal distribution with parameters µ and σ

∼L N (µ,σ

), if its density function is given by

f (x)

2πσ

exp

−

(log x −µ)

2σ

, x >0.

If Y has a normal distribution, then X

= e

is lognormal. Parameter µ is the

mean and

σ is the standard deviation of the distribution for the normal ran-

dom variable log X , not the lognormal random variable X , and this can some-

times be confusing.

The moments of the lognormal distribution can be computed from the

moment-generating function of the normal distribution. The nth moment is

E(X

) =exp{nµ +n

/2}, from which the mean and variance of X are

E(X ) =exp{µ +σ

/2}, and Var (X ) =exp{2(µ +σ

)} −exp{2µ +σ

The median is exp

{µ} and the mode is exp{µ −σ

The lognormality is preserved under multiplication and division, i.e., the

products and quotients of lognormal random variables remain lognormally

distributed. If X

∼L N (µ

,σ

), then

∼L N (

Several biomedical phenomena are well modeled by a lognormal distribu-

tion, for example, the age at onset of Alzheimer’s disease, latent periods of

infectious diseases, or survival time after diagnosis of cancer. For measure-

ment errors that are multiplicative, the convenient model is lognormal. More

applications and properties can be found in Crow and Shimizu (1988).

In MATLAB, the CDF of a lognormal distribution with parameters m

and s is evaluated at x as

logncdf(x,m,s), and the PDF is computed as

lognpdf(x,m,s). The pth percentile is computed with logninv(p,m,s). Here the

parameter

s stands for σ, not σ

. In WinBUGS, the lognormal distribution is

coded as

dlnorm(mu,tau), where tau stands for the precision parameter

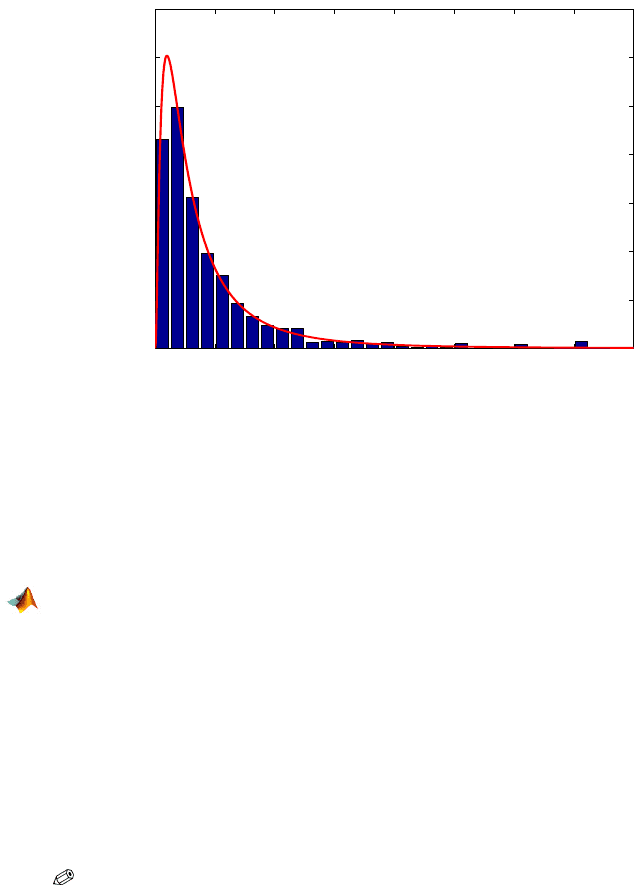
Example 6.10. Renner’s Honey Data. The content of hydroxymethylfurfurol

(HMF,

) in 1573 honey samples (Renner, 1970) is well conforming to the log-

normal distribution. The data set

renner.mat|dat contains the interval

midpoints (ﬁrst column) and interval frequencies (second column). The param-

eter

µ was estimated as − 0.6084 and σ as 1.0040. The histogram and ﬁtting

density are shown in Fig. 6.15 and the code is given in

renner.m.

6.7 Delta Method and Variance Stabilizing Transformations* 219

0 1 2 3 4 5 6 7 8

0.2

0.4

0.6

0.8

1.2

1.4

Fig. 6.15 Normalized histogram of Renner’s honey data and lognormal distribution with

parameters

µ =−0.6083 and σ

=1.0040

that ﬁts data well

The goodness of such ﬁtting procedures will be discussed in Chap. 13 more

formally. Note that

µ and σ are the mean and standard deviation of the loga-

rithms of observations, not the observations themselves.

load ’renner.dat’

% mid-intervals, int. length = 0.25

rennerx = renner(:,1);

% frequencies in the interval

rennerf = renner(:,2);

n = sum(renner(:,2)); % sample size (n=1573)

bar(rennerx, rennerf./(0.25

n))

hold on

m = sum(log(rennerx) .

rennerf)/n %m =-0.6083

s = sqrt( sum( rennerf .

(log(rennerx) - m).^2 )/n )

%s=1.0040

xx = 0:0.01:8;

yy = lognpdf(xx, m, s);

plot(xx, yy, ’r-’,’linewidth’,2)

6.7 Delta Method and Variance Stabilizing

Transformations*

The CLT states that for independent identically distributed random variables

,... , X

with mean µ and ﬁnite variance σ

220 6 Normal Distribution

n(X −µ)

approx

∼ N (0,σ

where the symbol

approx

∼ means distributed approximately as. Other than for a

ﬁnite variance, there are no restrictions on the type, distribution, or any other

feature of random variables X

For a function g

g(X ) − g(µ)

approx

∼ N (0, g

(µ)

The only restriction on g is that the derivative evaluated at

µ must be

ﬁnite and nonzero.

This result is called the delta method and the proof, which uses a simple

Taylor expansion argument, will be omitted since it also uses facts concerning

the convergence of random variables not covered in the text.

Example 6.11. For n large

approx

∼ N

approx

∼ N

,4µ

The delta method is useful for many asymptotic arguments. Now we focus on

the selection of the transformation g that stabilizes the variance.

Important statistical methodologies often assume that observations have

variances that are constant for all possible values of the mean. Observations

coming from a normal

N (µ,σ

) distribution would satisfy this requirement

since

does not depend on the mean µ. However, constancy of variances

with respect to the mean is rather an exception than the rule. For example,

if random variates from the exponential

E (λ) distribution are generated, then

the variance

=1/λ

depends on the mean µ =1/λ, as σ

=µ

For some important distributions we will ﬁnd the transformation that will

“free” the variance from the inﬂuence of the mean. This will prove beneﬁcial

for a range of inferential statistical procedures covered later in the text (conﬁ-

dence intervals, testing hypotheses).

Suppose that the variance

Var X = σ

(µ) can be expressed as a function of

the mean

µ = EX . For Y = g(X ), Var Y ≈ [g

(µ)]

(µ), see (5.12). The condi-

tion that the variance of Y is constant leads to a simple differential equation

(µ)]

(µ) = c

with the following solution:

6.7 Delta Method and Variance Stabilizing Transformations* 221

g(x) = c

(x)

dx. (6.4)

This is the theoretical basis for many proposed variance stabilizing trans-

forms. Note that

(x) in (6.4) is a function expressing the variance as a func-

tion of the mean.

Example 6.12. Stabilizing Variance. Suppose data are sampled from (a)

Poisson

P oi(λ), (b) exponential E (λ), and (c) binomial B in(n, p) distributions.

In (a), the mean and variance are equal,

(µ) =µ (=λ), and (6.4) becomes

g(x)

= c

=2c

x +d

for some constants c and d. Thus, as the variance stabilizing transformation

for Poisson observations one can take g(x)

In (b) and (c),

(

)

and

(

)

−

and, after solving the

integral in (6.4), one ﬁnds that the transformations are g(x)

= log(x) and

g(x)

=arcsin

x/n (Exercise 6.18).

Example 6.13. Box and Cox (1964) introduced a family of transformations, in-

dexed by a parameter

λ, applicable to positive data X

,... , X

(

−1

, λ 6=0

log X

, λ =0.

(6.5)

This transformation is mostly applied to responses in linear models exhibiting

nonnormality or heterogeneity of variances (heteroscedasticity). For properly

selected

λ, transformed data Y

,... , Y

may look “more normal” and amenable

to standard modeling techniques. The parameter

λ is selected by maximizing,

(

λ −1)

i=1

log X

−

log

i=1

−Y )

, (6.6)

where Y

are as given in (6.5) and Y =

As an illustration, we apply the Box–Cox transformation to apparently

skewed data of pyruvate kinase concentrations.

Exercise 2.16 featured a multivariate data set

dmd.dat in which the

fourth column gives pyruvate kinase concentrations in 194 female relatives

of boys with Duchenne muscular dystrophy (DMD). The distribution of this

measurement is skewed to the right (Fig. 6.16a). We will ﬁnd the Box–Cox

transform to symmetrize the data (make it approximately normal). Panel (b)

222 6 Normal Distribution

gives the values of likelihood in (6.6) for different values of λ. Note that (6.6)

is maximized for

λ approximately equal to –0.15. Figure 6.16c gives the his-

togram for data transformed by the Box–Cox transformation with

λ = −0.15.

The histogram is notably symmetrized. For details see

boxcox.m.

0 20 40 60 80 100 120

−1 −0.5 0 0.5

−425

−420

−415

−410

−405

−400

−395

−390

0.5 1 1.5 2 2.5 3 3.5

(a) (b) (c)

Fig. 6.16 (a) Histogram of row data of pyruvate kinase concentrations; (b) Log-likelihood is

maximized at

λ =−0.15; and (c) Histogram of Box-Cox-transformed data.

6.8 Exercises

6.1. Standard Normal Calculations. Random variable X has a standard nor-

mal distribution. What is larger,

P(|X |≤0.7) or P(|X |≥0.7)?

6.2. Nonnegative Deﬁniteness of

Σ Constrains ρ. Show that condition |Σ|≥

0 for Σ in (6.2), implies −1 ≤ρ ≤1.

6.3. Herrings. The alewife (Pomolobus pseudoharengus, Wilson 1811) grows

to a length of about 15 in., but adults average only about 10.5 in. long

and about 8 oz. in weight; 16,400,000 ﬁsh taken in New England in 1898

weighed about 8,800,000 lbs.

Fig. 6.17 Alewife ﬁsh.

6.8 Exercises 223

Assume that the length of an individual ﬁsh (Fig. 6.17) is normally dis-

tributed with mean 10.5 in. and standard deviation 1.6 in. and that the

weight is distributed as

with 8 degrees of freedom.

(a) What percentage of the ﬁsh are between 10.5 and 13 in. long?

(b) What percentage of the ﬁsh weigh more than 10 oz.?

6.4. Sea Urchins. In a laboratory experiment, researchers at Barry Univer-

sity, (Miami Shores, FL) studied the rate at which sea urchins ingested tur-

tle grass (Florida Scientist, Summer/Autumn 1991). The urchins starved

for 48 h, were fed 5-cm blades of green turtle grass. The mean ingestion

time was found to be 2.83 h and the standard deviation 0.79 h. Assume that

green turtle grass ingestion time for the sea urchins has an approximately

normal distribution.

(a) Find the probability that a sea urchin will require between 2.3 and 4 h

to ingest a 5-cm blade of green turtle grass.

(b) Find the time t

∗

(hours) so that 95% of sea urchins take more than t

∗

hours to ingest a 5-cm blade of green turtle grass.

6.5. Pyruvate Kinase for Controls Is Normal. Refer to Exercise 2.16. The

histogram for PK response for controls, X , is fairly bell-shaped (as much as

142 observations show), so you decided to ﬁt it with a normal distribution,

N (12,4

(a) How would you defend the choice of a normal model that allows for

negative values when the measured level is always positive?

(b) Find the probability that X falls between 4 and 20.

(d) Find the value x

so that 93% of all PK measurements exceed x

6.6. Leptin. Leptin (from the Greek word leptos, meaning thin) is a 16-kDa

protein hormone that plays a key role in regulating energy intake and

energy expenditure, including the regulation (decrease) of appetite and

(increase) of metabolism. Serum leptin concentrations can be measured

in several ways. One approach is by using a radioimmunoassay in ve-

nous blood samples (Linco Research Inc., St Charles, MO). Several studies

have consistently found women to have higher serum leptin concentrations

than do men. For example, among US adults across a broad age range,

the mean serum leptin concentration in women is approximately normal

N (12.7 µg/L, (1.3 µg/L)

) and in men approximately normal N (4.6 µg/L,

(0.5

µg/L)

(a) What is the probability that the concentration of leptin in a randomly

selected US adult male exceeds 6

µ g/L? (b) What proportion of US women

have concentration of leptin in the interval 12.7

±2 µ g/L? (c) What interval,

symmetric about the mean 12.7

µg/L, contains leptin concentrations of 95%

of adult US women?

224 6 Normal Distribution

6.7. Pulse Rate. The pulse rate of 1-month-old infants has a mean of 115 beats

per minute and a standard deviation of 16 beats per minute.

(a) Explain why the average pulse rate in a sample of 64 1-month-old in-

fants is approximately normally distributed.

(b) Find the mean and the variance of the normal distribution in (a).

exceed 120.

6.8. Side Effects. One of the side effects of ﬂooding a lake in northern boreal

forest areas

(e.g., for a hydroelectric project) is that mercury is leaked from

the soil, enters the food chain, and eventually contaminates the ﬁsh. The

concentration of mercury in ﬁsh will vary among individual ﬁsh because

of differences in eating patterns, movements around the lake, etc. Suppose

that the concentrations of mercury in individual ﬁsh follows an approxi-

mately normal distribution with a mean of 0.25 ppm and a standard devia-

tion of 0.08 ppm. Fish are safe to eat if the mercury level is below 0.30 ppm.

What proportion of ﬁsh are safe to eat?

a. 63.1% b. 23.8% c. 73.4% d. 27.3% e. 37.9%

6.9. Macrolepiota Procera. The size of mushroom caps varies. While many

species of Marasmius and Collybia are only 12 to 20 mm (1/2 to 3/4 in.) in

diameter, some fungi are nearly 200 mm (8 in.) across. The cap diameter

of parasol mushroom (Macrolepiota procera, Fig. 6.18) is a normal random

variable with parameters

µ =230 mm and σ =25 mm.

Fig. 6.18 Parasol mushroom Macrolepiota procera.

(a) What proportion of parasol caps has a diameter between 200 and

250 mm?

(b) Five percent of parasol caps are larger than x

in diameter. Find x

6.10. Duration of Gestation in Humans. Altman (1980) quotes the following

incident from the UK: “In 1949 a divorce case was heard in which the sole

The northern boreal forest, sometimes also called the taiga or northern coniferous forest,

stretches unbroken from eastern Canada westward throughout the majority of Canada to

the central region of Alaska.

6.8 Exercises 225

evidence of adultery was that a baby was born 349 days after the husband

had gone abroad on military service. The appeal judges agreed that medi-

cal evidence was unlikely but scientiﬁcally possible.” So the appeal failed.

“Most people think that the husband was hard done by,” Altman adds.

So let us judge the judges. The reported mean duration of an uncomplicated

human gestation is between 266 and 288 days, depending on many factors

but mainly on the method of calculation. Assume that population mean

and standard deviations are

µ = 280 and σ = 10 days, respectively. In fact,

smaller standard deviations have been reported, so 10 days is a conserva-

tive choice. The normal model ﬁts the data reasonably well if the samples

are large.

Under the normal

N (µ,σ

) model, ﬁnd the probability that a gestation pe-

riod will be equal to or greater than 349 days.

6.11. Tolerance Design. Eggert (2005) provides the following engineering de-

sign question. A 5-inch-diameter pin will be assembled into a 5.005 inch

journal bearing. The pin manufacturing tolerance is speciﬁed to t

=0.003

inch. A minimum clearance ﬁt of 0.001 inch is needed.

Determine tolerance required of the hole, t

hole

, such that 99.9% of the

mates will exceed the minimum clearance. Assume that manufacturing

variations are normally distributed. The tolerance is deﬁned as 3 standard

deviations.

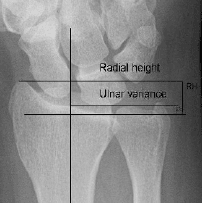
6.12. Ulnar Variance. This exercise uses data reported in Jung et al. (2001),

who studied radiographs of the wrists of 120 healthy volunteers in order to

determine the normal range of ulnar variance, Fig. 6.19. The radiographs

had been taken in various positions under both unloaded (static) and loaded

(dynamic) conditions.

Fig. 6.19 Ulnar variance (UV) is measured here using the method of perpendiculars, in

which two lines are drawn perpendicular to the long axis of the radius. One line is drawn

on the ulnar-side articular surface of the radius, and the other is drawn on the ulnar carpal

surface. This image shows positive UV.

The ulnar variance in neutral rotation was modeled by normal distribution

with a mean of

µ =0.74 mm and standard deviation of σ =1.46 mm.

226 6 Normal Distribution

(a) What is the probability that a radiogram of a normal person will show

negative ulnar variance in neutral rotation (ulnar variance, unlike the sta-

tistical variance, can be negative)?

The researchers modeled the maximum ulnar variance (UV

max

) as normal

N (1.52, 1.56

) when gripping in pronation and minimum ulnar variance

(UV

min

) as normal N (0.19, 1.43

) when relaxed in supination.

(b) Find the probability that the mean dynamic range in ulnar variance,

=UV

max

−UV

min

, will exceed 1 mm.

6.13. Independence of Sample Mean and Standard Deviation in Normal

Samples. Simulate 1000 samples from the standard normal distribution,

each of size 100, and ﬁnd their sample mean and standard deviation.

(a) Plot a scatterplot of sample means vs. the corresponding sample stan-

dard deviations. Are there any trends?

(b) Find the coefﬁcient of correlation between sample means and standard

deviations from (a) arranged as two vectors. Is the coefﬁcient close to zero?

6.14. Sonny and Multiple Choice Exam. An instructor gives a 100-question

multiple-choice ﬁnal exam. Each question has 4 choices. In order to pass, a

student has to have at least 35 correct answers. Sonny decides to guess at

random on each question. What is the probability that Sonny will pass the

exam?

6.15. Amount of Liquid in a Bottle. Suppose that the volume of liquid in a

bottle of a certain chemical solution is normally distributed with a mean of

0.5 L and standard deviation of 0.01 L.

(a) Find the probability that a bottle will contain at least 0.48 L of liquid.

(b) Find the volume that corresponds to the 95th percentile.

6.16. Meristem Cells in 3-D. Suppose that a particle is ﬁred at a cell sitting

at the origin of a spatial coordinate system, with units in microns. The

particle lands at (X ,Y , Z), where X ,Y , and Z are independent and each

has a normal distribution with a mean of

µ = 0 and variance of σ

= 250.

The particle is successfully delivered if it lands within 70

µm of the origin.

Find the probability that the particle was not successfully delivered.

6.17. Glossina morsitans. Glossina morsitans (tsetse ﬂy) is a large biting ﬂy

that inhabits most of midcontinental Africa. This ﬂy is infamous as the pri-

mary biological vector (the meaning of vector here is epidemiological, not

mathematical. A vector is any living carrier that transmits an infectious

agent) of trypanosomes, which cause human sleeping sickness. The data in

the table below are reported in Pearson (1914) and represent the frequen-

cies of length in microns of trypanosomes found in Glossina morsitans.

Microns 15 16 17 18 19 20 21 22 23 24 25

Frequency 7 31 148 230 326 252 237 184 143 115 130

Microns 26 27 28 29 30 31 32 33 34 35 Total

Frequency 110 127 133 113 96 54 44 11 7 2 2500