Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

6.2 Normal Distribution 197

6.2.1 Sigma Rules

Sigma rules state that for any normal distribution, the probability that an

observation will fall in the interval

µ ±kσ for k =1,2, and 3 is 68.27%,95.45%

and 99.73%, respectively. More precisely,

P(µ −σ < X <µ +σ) =P(−1 < Z <1) =Φ(1) −Φ(−1) =0.682689 ≈68.27%

P(µ −2σ < X <µ +2σ) =P(−2 < Z <2) =Φ(2) −Φ(−2) =0.954500 ≈95.45%

P(µ −3σ < X <µ +3σ) =P(−3 < Z <3) =Φ(3) −Φ(−3) =0.997300 ≈99.73%

Did you ever wonder about the origin of the term Six Sigma? It does not

involve

P(µ −6σ < X <µ +6σ) as one may expect.

The Six Sigma doctrine is a standard according to which an item with mea-

surement X

∼N (µ,σ

) should satisfy X <6σ to be conforming if µ is allowed

to vary between

−1.5σ and 1.5σ.

Thus effectively, accounting for the variability in the mean, the Six Sigma

constraint becomes

P(X <µ +4.5σ) = P(Z <4.5) =Φ(4.5) =0.99999660.

This means that only 3.4 items per million produced are allowed to exceed µ+

4.5σ (be defective). Such standard of quality was set by the Motorola company

in the 1980s, and it evolved into a doctrine for improving efﬁciency and quality

in management.

6.2.2 Bivariate Normal Distribution*

When the components of a random vector have a normal distribution, we say

that the vector has a multivariate normal distribution. For independent com-

ponents, the density of a multivariate distribution is simply the product of

the univariate densities. When components are correlated, the distribution in-

volves the covariance matrix that describes the correlation. Next we discuss

the bivariate normal distribution, which will be important later on, in the con-

text of correlation and regression.

The pair (X ,Y ) is distributed as bivariate normal

(µ

,µ

,σ

,ρ) if

the joint density is

f (x, y) =

2πσ

1 −ρ

exp

(

−

2(1 −ρ

)

(x −µ

)

−

2ρ(x −µ

)(y −µ

)

(y −µ

)

. (6.1)

The parameters µ

,µ

,σ

, and ρ are

=E(X ),µ

=E(Y ),σ

=Var (X ),σ

=Var (Y ), and ρ =Corr(X ,Y ).

One can deﬁne bivariate normal distribution with a density as in (6.1) by

transforming two independent, standard normal random variables Z

and Z

198 6 Normal Distribution

X = µ

+σ

= µ

+ρσ

1 −ρ

The marginal distributions in (6.1) are X

∼N (µ

,σ

) and Y ∼N (µ

,σ

The bivariate normal vector (X ,Y ) has covariance a matrix

Σ =

ρ σ

. (6.2)

The covariance matrix

Σ is nonnegative deﬁnite. A sufﬁcient condition for non-

negative deﬁniteness in this case is

|Σ|≥0 (see also Exercise 6.2).

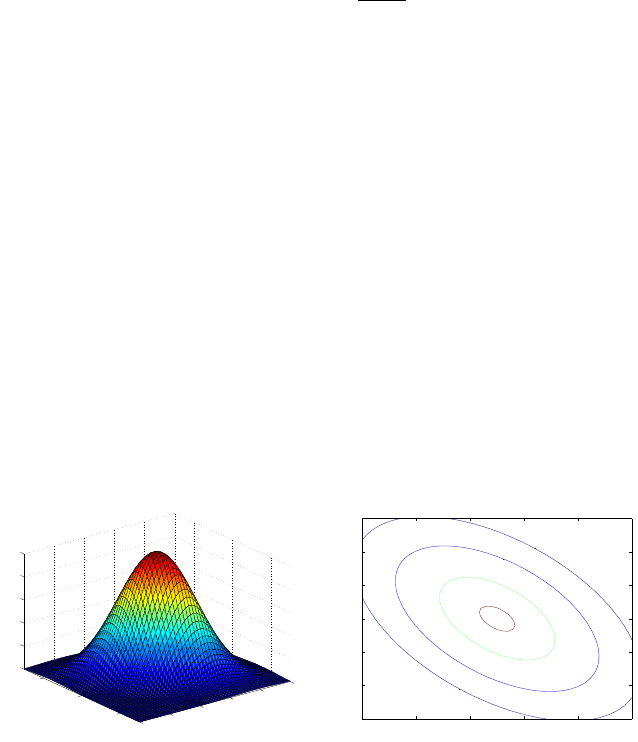
Figure 6.6a shows the density of a bivariate normal distribution with mean

µ =

−

and covariance matrix

Σ =

3 −0.9

−0.9 1

Figure 6.6b shows contours of equal probability.

−6

−4

−2

0.02

0.04

0.06

0.08

0.1

−6 −4 −2 0 2 4

−1

(a) (b)

Fig. 6.6 (a) Density of bivariate normal distribution with mean

mu=[-1 2] and covariance

matrix

Sigma=[3 -0.9; -0.9 1]. (b) Contour plots of a density at levels [0.001 0.01

0.05 0.1]

Several properties of bivariate normal are listed below.

(i) If (X ,Y ) is bivariate normal, then aX

+ bY has a univariate normal

distribution.

(ii) If (X ,Y ) is bivariate normal, then (aX

+bY , cX +dY ) is also bivariate

normal.

(iii) If the components in (X ,Y ) are such that

Cov(X ,Y ) =σ

ρ =0, then

X and Y are independent.

6.3 Examples with a Normal Distribution 199

(iv) Any bivariate normal pair (X , Y ) can be transformed into a pair

(U,V )

= (aX +bY , cX +dY ) such that U and V are independent. If σ

= σ

then one such transformation is U

= X +Y , V = X −Y . For an arbitrary bi-

variate normal distribution, the rotation

= X cosϕ −Y sinϕ

V = X sinϕ +Y cosϕ

makes components (U,V ) independent if the rotation angle ϕ satisﬁes

cot2

ϕ =

−σ

2σ

(v) If (X ,Y ) is bivariate normal, then the conditional distribution of Y when

= x is normal with expectation and variance

+ρ

(x −µ

), and σ

(1 −ρ

respectively. The linearity in x of the conditional expectation of Y will be the

basis for linear regression, covered in Chap. 16. Also, the fact that X

= x is

known decreases the variance of Y , indeed

(1 −ρ

) ≤σ

6.3 Examples with a Normal Distribution

We provide two examples with typical calculations involving normal distribu-

tions, with solutions in MATLAB and WinBUGS.

Example 6.1. IgE Concentration. Total serum IgE (immunoglobulin E) con-

centration allergy tests allow for the measurement of the total IgE level in a

serum sample. Elevated levels of IgE are associated with the presence of an

allergy. An example of testing for total serum IgE is the PRIST (paper radioim-

munosorbent test). This test involves serum samples reacting with IgE that

has been tagged with radioactive iodine. The bound radioactive iodine, cal-

culated upon completion of the test procedure, is proportional to the amount

of total IgE in the serum sample. The determination of normal IgE levels in a

population of healthy nonallergic individuals varies by the fact that some indi-

viduals may have subclinical allergies and therefore have abnormal serum IgE

levels. The log concentration of IgE (in IU/ml) in a cohort of healthy subjects is

distributed as a normal

N (9,(0.9)

) random variable. What is the probability

that in a randomly selected subject from the same cohort the log concentration

will

• Exceed 10 IU/ml?

• Be between 8.1 and 9.9 IU/ml?

200 6 Normal Distribution

• Differ from the mean by no more than 1.8 IU/ml?

• Find the number x

such that the IgE log concentration in 90% of the sub-

jects from the same cohort exceeds x

• In what bounds (symmetric about the mean) does the IgE log concentration

fall with a probability of 0.95?

• If the IgE log concentration is

N (9,σ

), ﬁnd σ so that

P(8

≤ X ≤10) =0.64.

Let X be the IgE log concentration in a randomly selected subject. Then

∼N (9,0.9

). The solution is given by the following MATLAB code ( ige.m):

%(1)

%P(X>10)= 1-P(X <= 10)

1-normcdf(10,9,0.9) %or 1-normcdf((10-9)/0.9)

%ans = 0.1333

%(2)

%P(8.1 <= X <= 9.9)

%P((8.1-9)/0.9 <= Z <= (9.9-9)/0.9)

%P(-1 <= Z <= 1) ::: Note 1-sigma rule.

normcdf(9.9, 9, 0.9) - normcdf(8.1, 9, 0.9)

%or, normcdf((9.9-9)/0.9)-normcdf((8.1-9)/0.9)

%ans = 0.6827

%(3)

%P(9-1.8 <= X <= 9+1.8) = P(-2 <= Z <= 2)

%Note 2-sigma rule.

normcdf(9+1.8, 9, 0.9) - normcdf(9-1.8, 9, 0.9)

% ans = 0.9545

%(4)

%0.90 = P(X > x

0)=1-P(X <= x0)

%that is P(Z <= (x0-9)/0.9)=0.1

norminv(1-0.9, 9, 0.9)

%ans = 7.8466

%(5)

%P(9-delta <= X <= 9+delta)=0.95

[9-0.9

norminv(1-0.05/2), 9+0.9

norminv(1-0.05/2)]

%ans = 7.2360 10.7640

%(6)

%P(-1/sigma) <= Z <= 1/sigma)=0.64

%note that 0.36/2 + 0.64 + 0.36/2 = 1

1/norminv( 1 - 0.36/2 )

%ans = 1.0925

Example 6.2. Aplysia Nerves. In this example, easily solved analytically and

using MATLAB, we will show how to use WinBUGS and obtain an approxi-

mate solution. The analysis is not Bayesian; WinBUGS will simply serve as a

random number generator and the required probability and quantile will be

found approximately by simulation.

6.3 Examples with a Normal Distribution 201

Fig. 6.7 Sea slug (Aplysia) neuron stained with membrane dye. From the cover of the 28

Characteristics of Aplysia nerves in response to extension were examined

in Koike (1987). Only the Aplysia nerve (Fig. 6.7) was easily elongated up to

about ﬁve times its resting or relaxing length without impairing propagation

of the action potential along the axon in the nerve. The conduction velocity

along the elongated nerve increased linearly in proportion to the nerve length

in a range from the relaxing length to about 1 to 1.5 times extension. For an

expansion factor of 1.5 the conducting velocity factors are normally distributed

with a mean of 1.4 and a standard deviation of 0.1. Using WinBUGS, we are

interested in ﬁnding

(a) the proportion of Aplysia nerves elongated by a factor of 1.5 for which

the conduction velocity factor exceeds 1.5;

(b) the proportion of Aplysia nerves elongated by a factor of 1.5 for which

the conduction velocity factor falls in the interval [1.35,1.61]; and

by a factor of 1.5.

#aplysia.odc

model{

mu <- 1.4

stdev <- 0.1

prec<- 1/(stdev

stdev)

y ~ dnorm(mu, prec)

propexceed <- step(y - 1.5)

propbetween <- step(y-1.35)

step(1.61-y)

#done in Sample Monitor Tool by

#selecting 95th percentile

}

There are no data to load; after the check model in Model>Specification go

directly to

compile, and then to gen inits. Update 10,000 iterations, and set

Sample Monitor Tool from Inference>Samples the nodes y, propexceed, and

202 6 Normal Distribution

propbetween. For part (c) select the 95th percentile in Sample Monitor Tool un-

der

percentiles. Finally, run the Update Tool for 1,000,000 updates and check

the results in

Sample Monitor Tool by setting a star (

) in the node window and

looking at

stats.

mean sd MC error val2.5pc median val97.5pc start sample

propbetween 0.6729 0.4691 4.831E-4 0.0 1.0 1.0 10001 1000000

propexceed 0.1587 0.3654 3.575E-4 0.0 0.0 1.0 10001 1000000

y 1.4 0.1001 1.005E-4 1.204 1.4 1.565 10001 1000000

Here is the same computation in MATLAB.

1-normcdf(1.5, 1.4, 0.1)

%ans = 0.1587

normcdf(1.61, 1.4, 0.1)-normcdf(1.35, 1.4, 0.1)

%ans = 0.6736

norminv(1-0.05, 1.4, 0.1)

%ans = 1.5645

6.4 Combining Normal Random Variables

Any linear combination of independent normal random variables is also nor-

mally distributed. Thus, we need only keep track of the mean and variance

of the variables involved in the linear combination, since these two param-

eters completely characterize the distribution. Let X

, X

,... , X

be indepen-

dent normal random variables such that X

∼N (µ

,σ

); then for any selection

of constants a

, a

,... , a

+···+a

i=1

∼N (µ,σ

where

µ = a

+···+a

i=1

+. .. a

i=1

6.4 Combining Normal Random Variables 203

Two special cases are important: (i) a

= 1, a

= −1 and (ii) a

= ··· = a

1/n. In case (i) we have a difference of two normals; its mean is the difference

of the corresponding means and variance is a sum of two variances. Case (ii)

corresponds to the arithmetic mean of normals,

X . For example, if X

,... , X

are i.i.d. N (µ,σ

), then the sample mean X = (X

+···+ X

)/n has a normal

N (µ,σ

/n) distribution. Thus, variances for X

s and X are related as

or, equivalently, for standard deviations

Example 6.3. The Piston Production Error. The proﬁle of a piston com-

prises a ring in which inner and outer radii X and Y are normal random vari-

ables,

N (20,0.01

) and N (30,0.02

), respectively. The thickness D =Y − X is

the random variable of interest.

(a) Find the distribution of D.

(b) For a randomly selected piston, what is the probability that D will ex-

ceed 10.04?

= 64 pistons, what is the probability

that

D will exceed 10.04? Exceed 10.004?

sqrt(0.01^2 + 0.02^2) %0.0224

1-normcdf((10.04 - 10)/0.0224) %0.0371

1-normcdf((10.04 - 10)/(0.0224/sqrt(64))) %0

1-normcdf((10.004 - 10)/(0.0224/sqrt(64))) %0.0766

Compare the probabilities of events {D > 10.04} and {D > 10.04}. Why is

the probability of

{D >10.04} essentially 0, when the analogous probability for

an individual measure D is 3.71%?

Example 6.4. Diluting Acid. In a laboratory, students are told to mix 100 ml

of distilled water with 50 ml of sulfuric acid and 30 ml of C

OH. Of course,

the measurements are not exact. The water is measured with a mean of 100 ml

and a standard deviation of 4 ml, the acid with a mean of 50 ml and a standard

deviation of 2 ml, and C

OH with a mean of 30 ml and a standard deviation

of 3 ml. The three measurements are normally distributed and independent.

(a) What is the probability of a given student measuring out at least 103

ml of water?

(b) What is the probability of a given student measuring out between 148

and 157 ml of water plus acid?

tween 175 and 180 ml of liquid?

204 6 Normal Distribution

1 - normcdf(103, 100, 4) %0.2266

normcdf(157, 150, sqrt(4^2 + 2^2)) ...

- normcdf(148, 150, sqrt(4^2 + 2^2)) %0.6139

normcdf(180, 180, sqrt(4^2 + 2^2 + 3^2 )) ...

- normcdf(175, 180, sqrt(4^2 + 2^2 + 3^2)) %0.3234

6.5 Central Limit Theorem

The central limit theorem (CLT) elevates the status of the normal distribu-

tion above other distributions. We have already seen that a linear combina-

tion of independent normals is the normal random variable itself. That is, if

,... , X

iid

∼N (µ,σ

), then

i=1

∼N (nµ, nσ

), and X =

i=1

∼N

µ,

The CLT states that X

,... , X

need not be normal in order for

or,

equivalently, for

X to be approximately normal. This approximation is quite

good for n as low as 30. As we said, variables X

, X

,... , X

need not be normal

but must satisfy some conditions. For CLT to hold, it is sufﬁcient for X

s to be

independent, equally distributed, and have ﬁnite variances and, consequently,

means. Other than that, the X

s can be arbitrary – skewed, discrete, etc. The

conditions of i.i.d. and ﬁniteness of variances are sufﬁcient – more precise

formulations of the CLT are beyond the scope of this course.

CLT. Let X

, X

,... , X

be i.i.d. random variables with ﬁnite means µ

and variances σ

. Then,

i=1

approx

∼ N (nµ, nσ

), and X =

i=1

approx

∼ N

µ,

A special case of CLT involving Bernoulli random variables results in a

normal approximation to binomials because the sum of many i.i.d. Bernoullis

is at the same time exactly binomial and approximately normal. This approx-

imation is handy when n is very large.

6.5 Central Limit Theorem 205

de Moivre (1738). Let X

, X

,... , X

be independent Bernoulli B er(p)

random variables with parameter p.

Then,

i=1

approx

∼ N (np, npq)

and

P(k

≤Y ≤ k

) =Φ

+1/2 −np

npq

−

−1/2 −np

npq

De Moivre’s approximation is good if both np and nq exceed 10 and n ex-

ceeds 30. If that is not the case, a Poisson approximation to binomial (p. 149)

could be better.

The factors 1/2 in de Moivre’s formula are continuity corrections. For ex-

ample, Y , which is discrete, is approximated with a continuous distribution.

P(Y ≤ k

+1) and P(Y < k

+1) are the same for a normal but not for a bino-

mial distribution for which

(

≤

)

Likewise,

(

≥

−

and

P(Y > k

−1) are the same for a normal but not for a binomial distribu-

tion for which

P(Y > k

−1) = P(Y ≥ k

). Thus, P(k

≤ Y ≤ k

) for a binomial

distribution is better approximated by

P(k

−1/2 ≤Y ≤ k

+1/2).

All approximations used to be much more important in the era before mod-

ern computing power was available. MATLAB is capable of calculating ex-

act binomial probabilities for huge values of n, and for practical reasons de

Moivre’s approximation is obsolete. For example,

format long

binocdf(1999988765, 4000000000, 1/2)

%ans = 0.361195130797824

format short

However, the theoretical value of de Moivre’s approximation is signiﬁcant

since many estimators and tests based on a binomial distribution can use well-

developed normal distribution machinery for an analysis beyond the compu-

tation.

The following MATLAB program exempliﬁes the CLT by averages of sim-

ulated uniform random variables.

% Central Limit Theorem Demo

figure;

subplot(3,2,1)

hist(rand(1, 10000),40) %histogram of 10000 uniforms

subplot(3,2,2)

hist(mean(rand(2, 10000)),40) %histogtam of 10000

206 6 Normal Distribution

%averages of 2 uniforms

subplot(3,2,3)

hist(mean(rand(3, 10000)),40) %histogtam of 10000

%averages of 3 uniforms

subplot(3,2,4)

hist(mean(rand(5, 10000)),40) %histogtam of 10000

%averages of 5 uniforms

subplot(3,2,5)

hist(mean(rand(10, 10000)),40) %histogtam of 10000

%averages of 10 uniforms

subplot(3,2,6)

hist(mean(rand(100, 10000)),40)%histogtam of 10000

%averages of 100 uniforms

0 0.2 0.4 0.6 0.8 1

100

200

300

0 0.2 0.4 0.6 0.8 1

200

400

600

0 0.2 0.4 0.6 0.8 1

200

400

600

0 0.2 0.4 0.6 0.8 1

200

400

600

800

0 0.2 0.4 0.6 0.8 1

200

400

600

800

0.4 0.5 0.6 0.7

500

1000

Fig. 6.8 Convergence to normal distribution shown via averages of 1, 2, 3, 5, 10, and 100

independent uniform (0,1) random variables

Figure 6.8 shows the histograms of 10,000 simulations of averages of

=1, 2,3,5,10, and 100 uniform random variables. It is interesting to see the

metamorphosis of a ﬂat single uniform (k

= 1), via a “witch hat distribution”

=2), into bell-shaped distributions close to the normal. For additional sim-

ulation experiments see the script

cltdemo.m.

Example 6.5. Is Grandpa’s Genetic Theory Valid? The domestic cat’s

wild appearance is increasingly overshadowed by color mutations, such as

black, white spotting, maltesing (diluting), red and tortoiseshell, shading, and

Siamese pointing. By favoring the odd or unusually colored and marked cats

over the “plain” tabby, people have consciously and unconsciously enhanced