Васильев К.К. Теория автоматического управления (следяшие системы)
Подождите немного. Документ загружается.


41
{}
)()( tXMtm = ,
{
}
2
))()()( tmtXMtD −= .
Так же, как и для случайной величины, дисперсия характери-
зует разброс значений случайного процесса относительно среднего
значения m(t). Чем больше D(t) , тем больше вероятность появле-
ния очень больших положительных и отрицательных значений
процесса. Более удобной характеристикой является среднее квадра-
тичное отклонение (СКО)
)()( tDt =
σ
, имеющее ту же размер-
ность, что и сам случайный процесс.
Если случайный процесс описывает, например, изменение
дальности до объекта, то математическое ожидание – средняя даль-
ность в метрах; дисперсия измеряется в квадратных метрах, а СКО
– в метрах и характеризует разброс возможных значений дальности
относительно средней.
Среднее значение и дисперсия являются
очень важными ха-
рактеристиками, позволяющими судить о поведении случайного
процесса в фиксированный момент времени. Однако, если необхо-
димо оценить «скорость» изменения процесса, то наблюдений в
один момент времени недостаточно. Для этого используют две слу-
чайные величины (X(t
1
), X(t
2
)), рассматриваемые совместно. Так же,
как и для случайных величин, вводится характеристика связи или
зависимости между X(t
1
)и X(t
2
). Для случайного процесса эта харак-
теристика зависит от двух моментов времени t
1
и t
2
и называется
корреляционной функцией:
{
}
))()()(()((),(
221121
tmtXtmtXMttR
−
−
= .
Стационарные случайные процессы
Многие процессы в системах управления протекают одно-
родно во времени. Их основные характеристики не изменяются.
Такие процессы называются
стационарными. Точное определение
можно дать следующим образом. Случайный процесс X(t) называ-
ется стационарным, если любые его вероятностные характеристи-
ки не зависят от сдвига начала отсчета времени. Для стационарного
случайного процесса математическое ожидание, дисперсия и СКО
постоянны: m(t) = m , D(t) = D=
σ
2
.

42
Корреляционная функция стационарного процесса не зависит
от начала отсчета t, т.е. зависит только от разности
12
tt −=
τ
мо-
ментов времени:
{
}
11
R( ) M (X(t ) m) (X(t ) m)
τ
τ
=−⋅−−.
Корреляционная функция стационарного случайного процес-
са имеет следующие свойства:
1)
2
=0)=R(
στ
; 2) )R(=)R(
τ
τ
−
; 3) 0)( =∞→
τ
R
.
Часто корреляционные функции процессов в системах управ-
ления имеют вид, показанный на рис. 27.
Интервал времени
τ
k
, на котором корреляционная функция,
т.е. величина связи между значениями случайного процесса,
уменьшается в М раз, называется
интервалом или временем кор-
реляции случайного процесса
. Обычно М=10 или М=е. Можно
сказать, что значения случайного процесса, отличающиеся по вре-
мени на интервал корреляции, слабо связаны друг с другом.
Таким образом, знание корреляционной функции позволяет
судить о скорости изменения случайного процесса.
Другой важной характеристикой является энергетический
спектр случайного процесса. Он определяется как преобразование
Фурье от
корреляционной функции:
∫
∞
∞−
−
=
ττω
ωτ
deRG
j
)()( .
Очевидно, справедливо и обратное преобразование:
∫
∞
∞−
=
ωω
π
τ
ωτ
deGR
j
)(
2
1
)(
.
Энергетический спектр показывает распределение мощности
случайного процесса, например помехи, на оси частот.
При анализе САУ очень важно определить характеристики
случайного процесса на выходе линейной системы при известных
Рис. 27
R(
τ
)
σ
2
τ
τ
k
0
σ
2
/е
43
характеристиках процесса на входе САУ. Предположим, что ли-
нейная система задана импульсной переходной характеристикой
()
τ
h
. Тогда выходной сигнал в момент времени
1
t определяется ин-
тегралом Дюамеля:
() ( )( )
∫
∞
∞−
−=
11111
τττ
dtghtx ,
где
()
tg
– процесс на входе системы. Для нахождения корреляцион-
ной функции
(
)
(
)
(
)
{
}
2121
, txtxMttR
x
=
запишем
() ()( )
∫
∞
∞−
−=
22222
ττ
dtgthtx и после перемножения найдем математи-
ческое ожидание
() ()()( )( ){}
∫∫
∞
∞−
∞
∞−
−−=
2122112121
,
ττττττ
ddtgtgMhhttR
x
.
Таким образом, связь между корреляционными функциями
входного и выходного случайных процессов устанавливается с по-
мощью следующего двойного интеграла:
() ()()( )
∫∫
∞
∞−
∞
∞−
−−=
2122112121
,,
ττττττ
ddttRhhttR
gx
.
Для стационарных процессов корреляционные функции зави-
сят только от разности аргументов
utt
=
−
21
,
(
)( )
vtt
=
−−
−
2211
τ
τ
и
поэтому
() ( )( ) ()
∫∫
∞
∞−
∞
∞−
=
2121
ττττ
ddvRhhuR
gx
.
Более простое соотношение можно найти для энергетических
спектров
)(
ω
g
G и )(
ω
x
G входного и выходного сигналов при из-
вестной передаточной функции
(
)
ω
jW линейной системы. Дейст-
вительно, найдем преобразование Фурье от левой и правой частей
последнего равенства. Получим следующее выражение:
() ()() ()
12 12xg
ju
GhhRedddu
ω
ωττνττ
∞∞∞
−∞ −∞ −∞
−
=
∫∫∫
.
После замены переменной
(
)
212121
τ
τ
τ
τ
−−=
−
−
−
=
uttv или
21
τ
τ
−+= vu
тройной интеграл преобразуется в произведение
44
() () ( ) ()
1122
12
x g
jj
jv
GhedhedRvedv
wt wt
w
wt ttt
ҐҐҐ
- Ґ - Ґ - Ґ
-
-
жцжцж
ц
чч
ч
ззз
чч
ч
ззз
=
чч
ч
ззз
чч
ч
чч
ч
ззз
ишиши
ш
ттт
.
Поскольку преобразование Фурье от импульсной характеристики
дает передаточную функцию, находим окончательно связь между
энергетическими спектрами процессов на входе и на выходе ли-
нейной системы:
() ( )
(
)
(
)
)()(
2
ωωωωωω
ggx
GjWGjWjWG =−= .
Часто помехи в системах управления имеют очень широкий
спектр. В таких случаях их удобно представить в виде так называе-
мого белого шума – процесса с постоянным энергетическим спек-
тром: G(
ω) = N
o
. Корреляционная функция белого шума
)()(
0
τ
δ
τ
NR = , где
δ
(t) – импульсная дельта-функция. Это означает,
что даже очень близкие по времени значения белого шума не свя-
заны друг с другом.
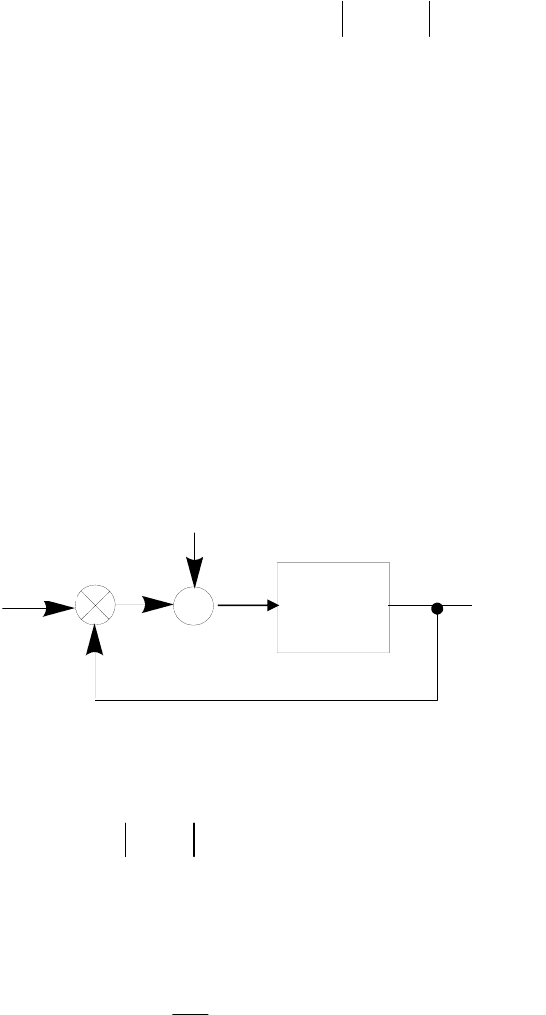
Воздействие помех на системы управления
Рассмотрим воздействие помехи n(t) на замкнутую линей-
ную систему управления (рис. 28). Будем предполагать, что нам из-
вестен энергетический спектр G
n
(ω) помехи.
Найдем дисперсию ошибки, возникающей при действии по-
мехи n(t). Для этого вначале определим энергетический спектр на
выходе системы
2
() () ()
вых n
GWpG
ω
ω
= , где W(p) = H(p) / (1+H(p)) –
передаточная функция замкнутой системы управления. После этого
с помощью обратного преобразования Фурье можно найти корре-
ляционную функцию помехи на выходе системы:
1
() ( )
2
j
вых вых
R
Ged
ωτ
τ
ωω
π
∞
−∞
=
∫
.
+
Рис. 28
g(t)
n(t)
H(p)
X(t)
+
-

45
Наконец, учитывая, что дисперсия
2
(0)
вых вых
R
σ
= , получаем оконча-
тельное выражение для дисперсии ошибки системы управления:
2
1
() .
2
вых
Gd
σ
ωω
π
∞
−∞
=
∫
Пример. Пусть на входе системы, содержащей один интегра-
тор, например, в системе управления приводом, действует широко-
полосная помеха с энергетическим спектром G
n
(ω) = N
o
. Переда-
точная функция системы с одним интегратором
Hp
k
p
()= . Опреде-
лим дисперсию ошибки, вызванной действием помехи. Для этого
вначале запишем выражение для передаточной функции замкнутой
системы
kp
k
pH
pH
pW
+
=
+
=
)(1
)(
)(
и найдем квадрат ее модуля:
.)(
22
2
k
k
pW
+
=
ω
Энергетический спектр помехи на выходе рас-
сматриваемой системы
2
2
0
22
() () () .
вых n
k
GWpG N
k
ωω
ω
==⋅
+
Таким образом, дисперсия ошибки САУ, вызванной действием
помехи, находится по формуле:
.
2
1
1
22
1
0
2
0
22
0
2
2
kN
z
dz
kN
d
k
Nk
вых
=
+
=
+
=
∫∫
∞
∞−
∞
∞−
π
ω
ω
π
σ
Описание траекторий движения объектов
с помощью случайных процессов
Входные сигналы САУ часто могут быть представлены с по-
мощью типовых детерминированных воздействий. Например, дви-
жение объекта с известной постоянной скоростью определяется
уравнением
(
)
0
gt g vt=+. Однако изменение входных сигналов во
времени не всегда может быть задано с помощью известных детер-
минированных функций. Во многих случаях для более реалистич-
ного описания, например, траектории движения самолета или ко-
рабля, необходимо использовать случайные процессы. При этом
известная детерминированная составляющая входного сигнала мо-

46
жет рассматриваться как математическое ожидание
()
tm случайного
процесса:
()
(
)
(
)
tgtmtg
0
+
=
,
где
()
tg
0
– стационарный случайный процесс с нулевым математи-
ческим ожиданием и корреляционной функцией
(
)
τ
g
R .
Таким образом, второе слагаемое
(
)
tg
0
описывает неизвест-
ный нам до эксперимента входной сигнал САУ в виде реализаций
случайного процесса. Корреляционная функция этого случайного
процесса позволяет задать дисперсию
(
)
0R
g
2
g
==
τσ
и «среднюю
скорость» изменения входного сигнала, связанную с интервалом
корреляции процесса
()
tg
0
. На практике приближенные значения
()
tm и
()
τ
g
R можно получить экспериментально, если в распоряже-
нии разработчика системы имеется большое число N записей
()
N,...,2,1k,tg
)k(
=
, реальных входных сигналов. Математическое
ожидание в этом случае оценивается средним арифметическим
() ()
∑
=
=
N
1k
)k(*
tg
N
1
tm ,
а для оценки корреляционной функции используется следующая
формула:
() () ( )
∑
=
+=
N
1k
)k()k(
*
g
tgtg
N
1
R
ττ
.
Процесс
()
tg
0
можно считать стационарным, если результаты рас-
четов по этой формуле мало зависят от выбора начала отсчета вре-
мени t.
Пусть входной сигнал САУ задан в виде суммы
() () ()
tgtmtg
0
+= . Для нахождения динамических ошибок, возни-
кающих в линейной системе управления, можно воспользоваться
принципом суперпозиции. Величина установившейся динамиче-
ской ошибки за счет детерминированной составляющей изменения
входного сигнала находится по известной формуле:
(
)
pplim
0p
уст
ε
ε
→
=
,
где
() () ()
pmpHp
ε
ε
= ;
()
()
pH1
1
pH
+
=
ε
– передаточная функция по
ошибке;
()
pm – изображение
(
)
tm по Лапласу.

47
Случайная составляющая характеризуется величиной дис-
персии динамической ошибки:
(
)
0R
2
==
τσ
εε
.
Для нахождения корреляционной функции
(
)
τ
ε
R
случайной состав-
ляющей динамической ошибки вначале находят энергетический
спектр
()
ω
g
G процесса
(
)
tg
0
как преобразование Фурье
()
τ
g
R . После
этого легко находятся энергетический спектр
(
)
(
)
(
)
ωωω
εε
g
2
GjHG =
и корреляционная функция динамической ошибки
() ()
ωω
π
τ
ωτ
εε
deG
2
1
R
j
∫
∞
∞−
= .
Суммарное воздействие детерминированного
()
tm и случай-
ного
()
tg
0
входного сигнала
(
)
tg
может быть оценено средним квад-
ратом динамической ошибки
(
)
(
)()
{
}
22
уст
2
txtgM
ε
σε
+=− .
Пример 1. Предположим, что на САУ (рис. 28) с одним инте-
гратором (
()
p/kpH
=
) поступает входной сигнал
() ()
tgvttg
0
+= , где
()
tg
0
– случайный процесс с корреляционной функцией
()
τ
στ
a
2
gg
eR
−
= . Определим в отсутствие помех (
()
0tn ≡ ) средний
квадрат динамической ошибки такой системы управления.
Вначале найдем установившуюся ошибку за счет детермини-
рованного слагаемого
()
vttm
=
входного воздействия. Для системы
с астатизмом первого порядка
k/v
уст
=
ε
. Энергетический спектр
()
ω
g
G случайной составляющей
(
)
tg
0
входного воздействия нахо-
дится как преобразование Фурье корреляционной функции:
() ()
2
22
2
g
j
gg
a
GRed
a
ωτ
σ
ωττ
ω
∞
−
−∞
==
+
∫
.
Заметим, что
aT
k
/1= является интервалом корреляции случайного
процесса
()
tg
0
на уровне e
/
1 . С другой стороны, параметр a равен
ширине энергетического спектра случайного процесса
(
)
tg
0
на
уровне 0.5, т.е.
()
(
)
5.00G/aG
gg
=
=
=
ω
ω
.
После нахождения энергетического спектра случайной со-
ставляющей динамической ошибки

48
() ( ) ()
()
()
()()
22
2
g
22
2
g
2
g
2
a
a2
k
G
jH1
1
GjHG
++
=
+
==
ω
σ
ω
ω
ω
ω
ωωω
εε
находим дисперсию динамической ошибки
() ()
ka
a
dG
2
1
0R
2
g
2
+
===
∫
∞
∞−
σ
ωω
π
σ
εεε
.
Средний квадрат динамической ошибки с учетом детерминирован-
ной и случайной составляющих определяется как сумма
k
a
a
k
v
2
g
2
2
22
уст
+
+=+
σ
σε
ε
.
Из полученного выражения следует, что при заданных параметрах
2
,,
g
av
σ
входного сигнала уменьшение динамической ошибки
достигается при увеличении коэффициента k усиления звена САУ.
Оптимизация параметров системы управления
Динамические ошибки при описании входного сигнала де-
терминированными функциями
(
)
pg в установившемся режиме оп-
ределяются по формуле:
(
)
(
)
pgpH
p
уст
ε
ε
0
lim
→
=
,
где
()
()
pH1
1
pH
+
=
ε
;
()
pH - передаточная функция разомкнутой САУ.
При описании входного сигнала реализациями случайного процесса
()
tg
0
динамические ошибки характеризуются величиной дисперсии
() ()
ωωω
π
σ
εε
dGjH
2
1
g
2
2
∫
∞
∞−
= ,
где
()
ω
g
G - энергетический спектр входного сигнала
()
tg
0
. При на-
личии детерминированных
(
)
tm и случайных
(
)
tg
0
составляющих
входного сигнала
() ()
(
)
tgtmtg
0
+
=
величину динамических ошибок
целесообразно оценивать средним квадратом суммарной ошибки
22
уст
ε
σε
+ .
Кроме динамических, в САУ имеются ошибки, вызванные
действием помех
()
tn . Влияние помех можно характеризовать

49
дисперсией
2
вых
σ
выходного сигнала САУ
() ()
ωωω
π
σ
dGjW
2
1
n
2
n
2
вых
∫
∞
∞−
= ,
где
()
ω
jW
n
- передаточная функция по помехе;
()
ω
n
G - энергетиче-
ский спектр помехи. Как правило, помехи в САУ могут быть пред-
ставлены белым шумом с постоянным на всех частотах энергетиче-
ским спектром
()
0n
NG =
ω
. Кроме того, помехи часто действуют на
вход системы и тогда передаточная функция по помехе
()
ω
jW
n
сов-
падает с передаточной функцией
()
(
)
()
ω
ω
ω
jH1
jH
jW
+
=
замкнутой САУ.
Во всех современных САУ присутствуют как динамические
ошибки, так и ошибки за счет действия помех. Для характеристики
качества системы управления при наличии динамических и случай-
ных ошибок используют средний квадрат суммарной ошибки:
2
вых
22
уст
2
с
σσεε
ε
++= ,
который зависит от параметров
aaa a
m
T
= ( , ,..., )
12
системы. Парамет-
ры
a обычно выбираются таким образом, чтобы обеспечить усло-
вие минимума квадрата суммарной ошибки
min
a
С
ε
2
. В этом случае
говорят об оптимизации параметров системы управления по крите-
рию минимума квадрата суммарной ошибки.
Пример 2. Рассмотрим систему привода антенны или рулей
летательного аппарата (см. п. 1.1), находящуюся под воздействием
помех (рис. 29).
Рис. 29
В такой системе угол поворота
х(t) вала двигателя должен
повторять заданную траекторию движения – входной сигнал g(t).
К
у
g(t)
n(t)
u(t)
x(t)
+
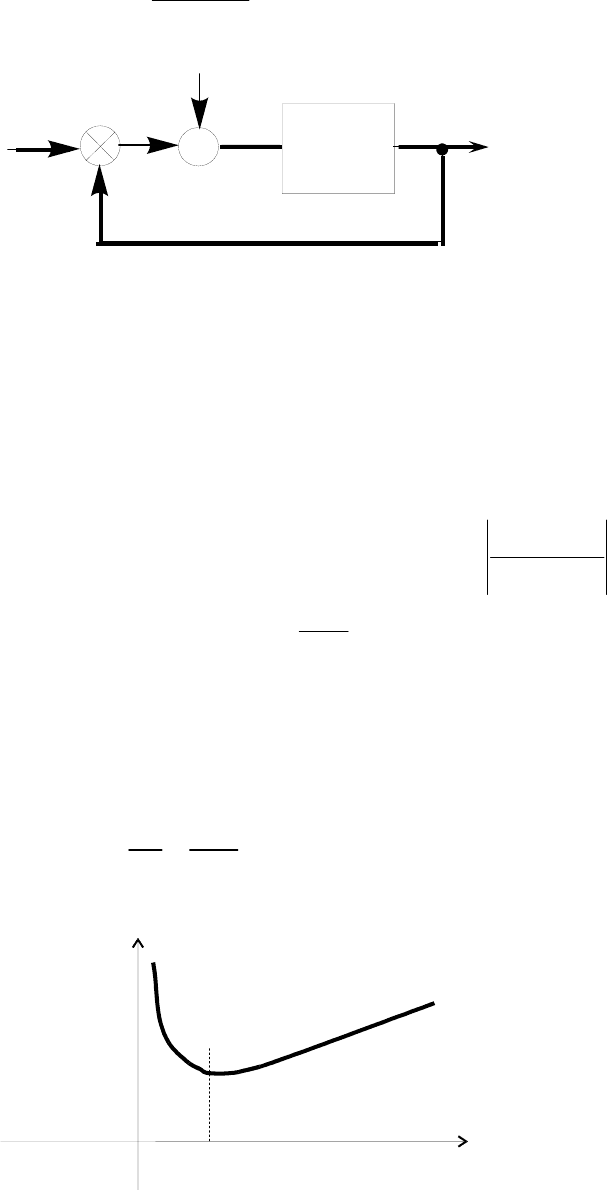
50
Помеха n(t) в данном случае описывает погрешности измерения
х(t).
Упрощенная эквивалентная схема такой системы представ-
лена на рис. 30, где
Hp
k
ppT
()
()
=
+1
, k=к
у
к
дв
– коэффициент пере-
дачи системы; Т – постоянная времени двигателя.
Рис. 30
Предположим, что заданная траектория движения описыва-
ется линейной функцией g(t)=Vt. Тогда установившиеся динамиче-
ские ошибки системы с одним интегратором определяются по фор-
муле
ε
уст
Vk= / . Чем выше коэффициент усиления k , тем меньше
величина динамической ошибки в установившемся режиме.
Будем аппроксимировать помеху белым шумом со спек-
тральной плотностью G
n
(ω)=N
0
. Тогда G
вых
(ω)=
Hj
Hj
N
()
()
ω
ω1
2
0
+
и
после преобразований находим:
σ
ε
2
0
2
=
NK
. Из этой формулы следу-
ет, что для уменьшения влияния помех необходимо снижать коэф-
фициент усиления k, т.е. повышать инерционность системы управ-
ления.
Квадрат суммарной ошибки определяется следующим выра-
жением:
2
22 2
0
2
2
c уст вых
VNk
k
εε σ
=+=+
. На основе этой формулы можно
построить график зависимости
εε
СС
k
22
= () (рис. 31).
k
0
k
n(t)
0
g(t) x(t)
H(p)
+
Рис. 31
+
–
2
c
ε
