Васильев К.К. Теория автоматического управления (следяшие системы)
Подождите немного. Документ загружается.


61
Рис. 36
После этого с помощью уравнения Винера найдем переда-
точную функцию H
2
(jω) и выделим ее реализуемую часть H
2P
(jω).
Общая передаточная функция оптимальной реализуемой системы
запишется в виде: W(j
ω)=H
1
(jω) H
2P
(jω).
Каким же образом превратить
z(t) в белый шум с помощью
фильтра? Нам известен энергетический спектр G
z
(ω)=G
g
(ω)+G
n
(ω).
Необходимо, чтобы
()
2
11
()
z
GHj N
ωω
=
, где N
1
- спектральная плот-
ность белого шума
z
1
, например, N
1
=1. Запишем это выражение
по-другому. Представим энергетический спектр G
z
(ω) в виде про-
изведения
() ( )( )
z
Gjj
ω
ψωψ ω
=−
, а
()
2
111
()( )
Hj
H
j
H
j
ω
ωω
=−
. Тогда
требуется, чтобы
()( )
(
)
(
)
11
1jjHjHj
ψ
ωψ ω ω ω
−
−=.
Для этого необходимо выбрать фильтр с передаточной функ-
цией
()
1
()1Hj j
ω
ψω
=
. Такой фильтр превращает входное воздейст-
вие в белый шум и называется
обеляющим. Заметим, что введение
обеляющего фильтра не приводит к потере оптимальности систе-
мы. Действительно, всегда можно восстановить входной сигнал с
помощью фильтра с передаточной функцией
(
)
1
H
j
ω
. Вместе с тем,
преобразование
()
zt в белый шум
(
)
1
zt позволяет построить опти-
мальную реализуемую систему. Для этого из уравнения Н.Винера
найдем передаточную функцию
(
)
2
H
j
ω
оптимальной нереализуе-
мой системы, выделим реализуемую часть и в результате получим
оптимальный реализуемый фильтр Винера. Наиболее просто это
осуществляется, если помеха n(t) является белым шумом со спек-
тральной плотностью N
0
.
Тогда передаточная функция оптимального реализуемого
фильтра записывается в виде
Wj
N
j
P
()
()
ω
ψω
=−1
0
. Для по-
строения такого фильтра достаточно представить энергетический
спектр G
z
(ω)=G
g
(ω)+N
0
в виде произведения двух комплексно-
+
H
1
(j
ω
) H
2
(j
ω
)
z
1
(t) x(t)
g(t)
n(t)
z(t)
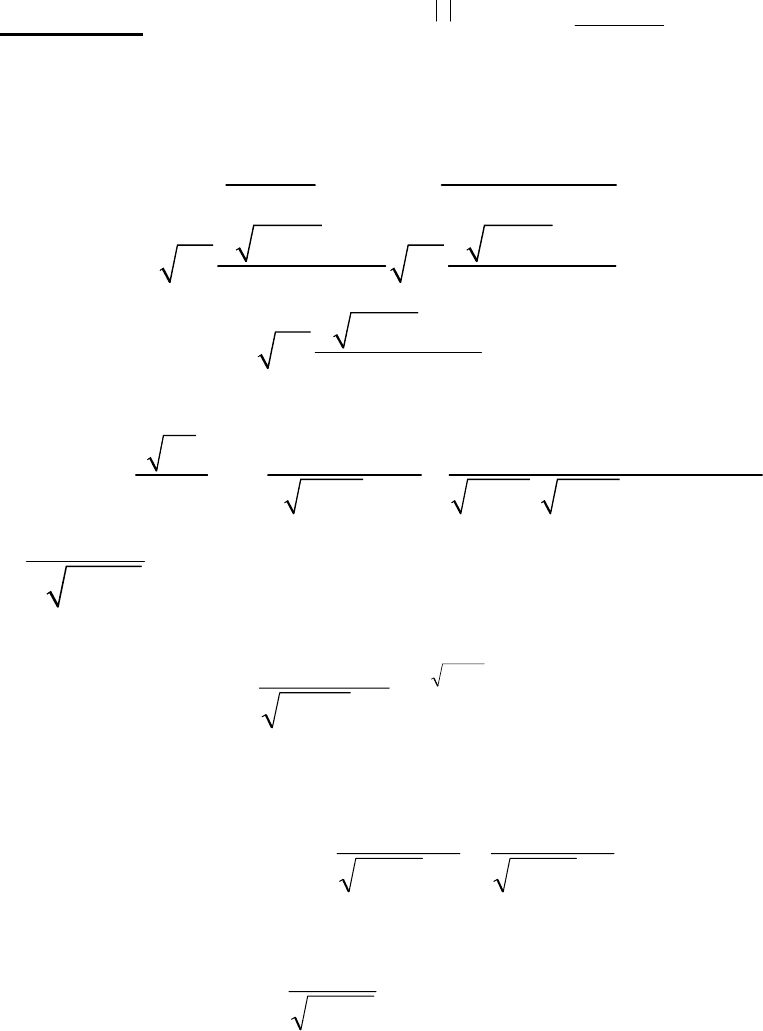
62
сопряженных сомножителей
Gjj
z
() ( )( )
ω
ψ
ω
ψ
ω
=
−
и воспользо-
ваться записанной формулой для передаточной функции оптималь-
ной реализуемой системы управления.
Пример 2. Пусть
τ
στ
a
2
gg
e)(R
−
= ,
0n
22
2
g
N)(G,
a
w
ga2
)(G =
+
=
ω
σ
ω
.
Разложим
GGG
zgn
() () ()ωω
ω
=+
на комплексно-сопряженные множи-
тели:
222
00
22 22
2(12)
()
z
ag a q
GNN
aa
σω
ω
ω
ω
++
=+= =
++
=
00
12 12aqj aqj
NN
aj aj
ω
ω
ωω
++ +−
+−
.
Таким образом,
0
12
()
aqj
jN
aj
ω
ψ
ω
ω
++
=
+
. Найдем теперь переда-
точную функцию оптимального реализуемого фильтра:
0
2
()1 1 ,
()
12 12(12 1)(1 )
P
N
aj q
Wj
j
aqj q q jT
ω
ω
ψω
ωω
+
=− =− =
++ + ++ +
где
1
12
T
aq
=
+
. Импульсная характеристика такого фильтра оп-
ределяется с помощью обратного преобразования Фурье:
τ
τ
q21a
e
1q21
aq2
)(h
+−
++
=
, 0≥
τ
.
Точно так же, как и раньше, может быть найдена минимально
достижимая дисперсия ошибки реализуемой системы:
1q21
2
1q21
aqN2
)0(hN
2
g
0
0
2
P0
++
=
++
==
σ
σ
.
Заметим, что найденная дисперсия ошибки
2
OP
σ
больше, чем
дисперсия ошибки
q21
2
g
2
mino
+
=
σ
σ
нереализуемой системы управле-
ния (см. пример 1).
Таким образом, подход Винера хотя и с дополнительными
усложнениями, но все-таки дает возможность построения физиче-
ски реализуемой системы управления и определения ее точностных
характеристик для стационарных входных воздействий и бесконеч-
ного времени наблюдения.
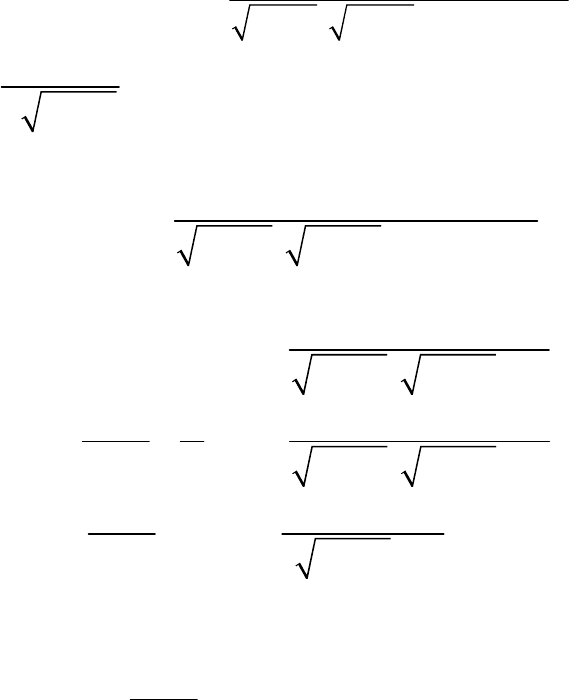
63
Фильтр Калмана для стационарных процессов
Полученное в последнем примере решение задачи синтеза
оптимальной реализуемой системы дает возможность определить
импульсную переходную характеристику
(
)
h
τ
или передаточную
функцию
()
p
Wj
ω
. Вместе с тем, существует еще одна форма пред-
ставления оптимальной системы с помощью дифференциального
уравнения. На это обстоятельство в 1959 г. обратил внимание
Р. Калман. Помимо простоты реализации оптимальных САУ для
определенного, но достаточно широкого класса входных сигналов,
метод Р. Калмана позволяет произвести синтез оптимальных мно-
гомерных нестационарных САУ.
Рассмотрим вначале
возможности описания оптимальной
системы, с помощью дифференциального уравнения. Как было ус-
тановлено, передаточная функция оптимальной реализуемой сис-
темы управления записывается в виде:
2
() ,
12(12 1)(1 )
P
q
Wj
qq jT
ω
ω
=
++++
где
1
.
12
T
aq
=
+
При этом выходной сигнал
() ()()
P
xp W pzp
=
или
2
() ()
12(12 1)(1 )
q
xp zp
qq pT
=
++++
.
После несложных преобразований:
2
() () ()
12(12 1)
q
xp pTxp zp
qq
+=
+++
,
() 1 2 /
() ()
12(12 1)
dx t q T
xt zt
dt T
qq
+=
+++
,
() 2
() ( () ())
(1 2 1)
dx t aq
ax t z t x t
dt
q
+= −
++
,
получим следующее дифференциальное уравнение, описывающее
оптимальную систему:
1
0
()
() ( () ())
dx t
ax t VN z t x t
dt
−
=− + −
,
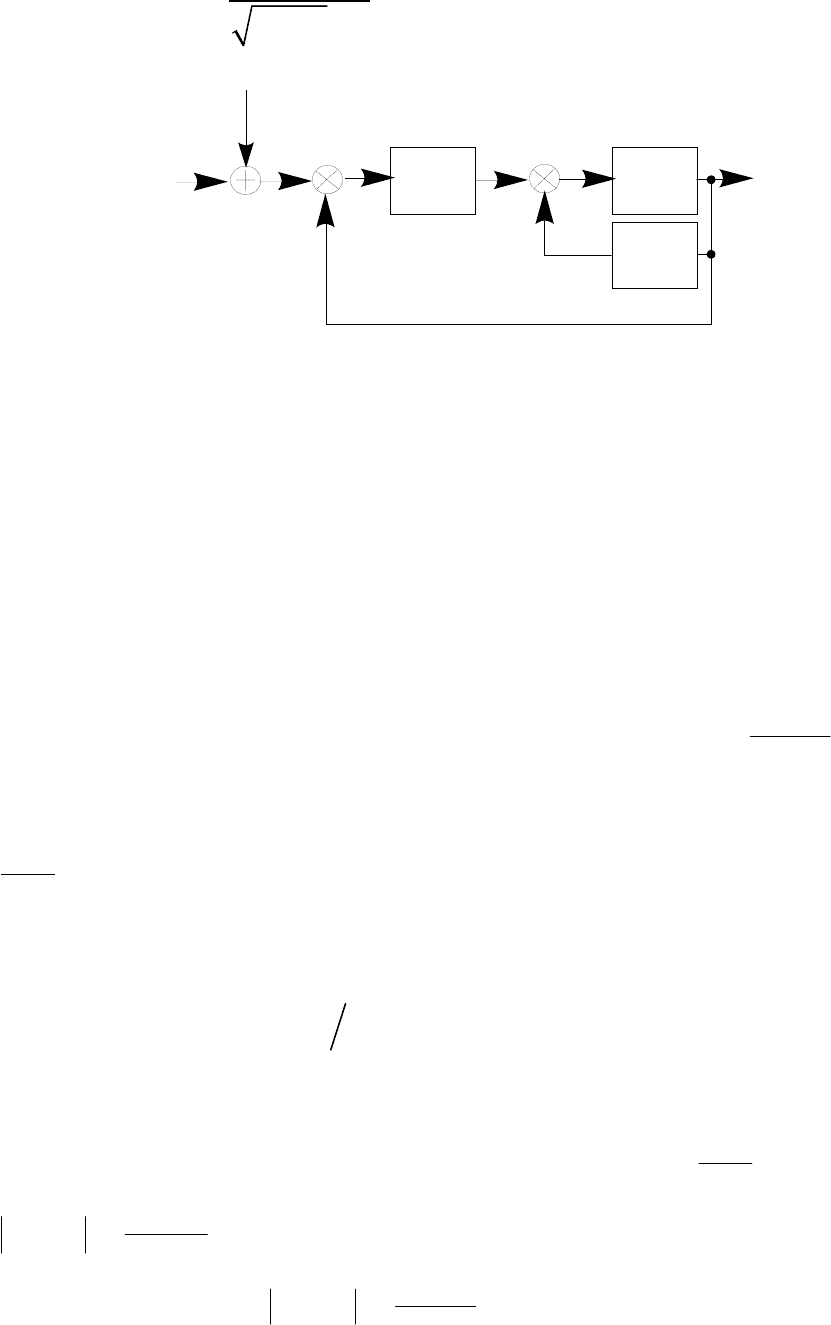
64
где
2
2
0
2
.
12 1
g
P
V
q
σ
σ
==
++
Такую систему можно представить с
помощью структурной схемы на рис.37, где K=VN
0
-1
.
Рис. 37
Эта структурная схема и является решением Калмана рассматри-
ваемой задачи. Оказывается, процедуру оптимального управления
можно представить в виде системы с обратной связью. Очень важ-
но, что структура не изменяется и остается оптимальной, если из-
меняются параметры сигналов и помех, а также на этапе переход-
ного процесса. В этих случаях
оптимальная система (рис. 37) ста-
новится системой с переменными параметрами k=k(t) и
).(
t
aa =
Р. Калман обратил также внимание, что часть системы
управления полностью определяется видом входного сигнала. Дей-
ствительно, если спектр входного воздействия
G
ag
a
g
()ω
σ
ω
=
+
2
2
22
, то та-
кое воздействие может быть сформировано из белого шума
ξ(t) с
помощью фильтра, описываемого дифференциальным уравнением
dg t
dt
ag t a t
()
() ()+=ξ
.
Найдем величину
ξ
N энергетического спектра белого шума
()
t
ξ
, обеспечивающего формирование сигнала
(
)
gt с заданным
спектром
()
()
222
2
gg
Ga a
ωσω
=+. После преобразования по Лап-
ласу дифференциальное уравнение запишется в виде
()p
g
a
g
ap
ξ
+=
– энергетический спектр. При этом передаточная
функция соответствующего фильтра
Hp
a
pa
ϕ
()=
+
или
Hj
a
a
ϕ
ω
ω
()
2
2
22
=
+
. Таким образом, спектр сигнала
()
gt на выходе
фильтра
GNHj
Na
wa
g
() ( )ωω
ξ
ϕ
ξ
==
+
2
2
22
, т.е. для полного соответствия
К
a
+
-
-
+
+
g(t)
n(t)
x(t)
z(t)
∫
0
t

65
спектру входного воздействия достаточно выбрать
22
2
ξ
=σNa ag
или
2
2=
g
Na
ξ
σ
.
С другой стороны, рассмотренное дифференциальное урав-
нение можно представить как уравнение, описывающее систему с
обратной связью, показанную на рис. 38.
Рис. 38
Сравним структурные схемы оптимальной САУ (рис. 37) и
полученной системы (рис.38), формирующей входной сигнал g(t) .
Анализ структурных схем и связанных с ними дифференциальных
уравнений показывает полное соответствие формирующего фильт-
ра и значительной части структуры оптимальной САУ.
* * *
Таким образом, Р.Калман предложил другое представление
для решения задачи построения оптимальной системы управления,
данной Н.Винером. Но это представление решения в виде замкну-
той системы, близкой по виду к формирующему фильтру, имело
далеко идущие последствия. Было установлено, что структура сис-
темы управления не изменяется и при управлении одновременно
несколькими
параметрами, а также при нестационарных воздейст-
виях. Эта структура сохраняется и остается оптимальной для ши-
рокого класса возможных входных сигналов и помех.
3.3. МНОГОМЕРНЫЕ ОПТИМАЛЬНЫЕ СИСТЕМЫ
Вначале подытожим основные результаты, полученные при
решении задачи синтеза одномерной оптимальной реализуемой
системы управления.
ξ()t
a
a
Х
g(t)
t
0
∫
+
-
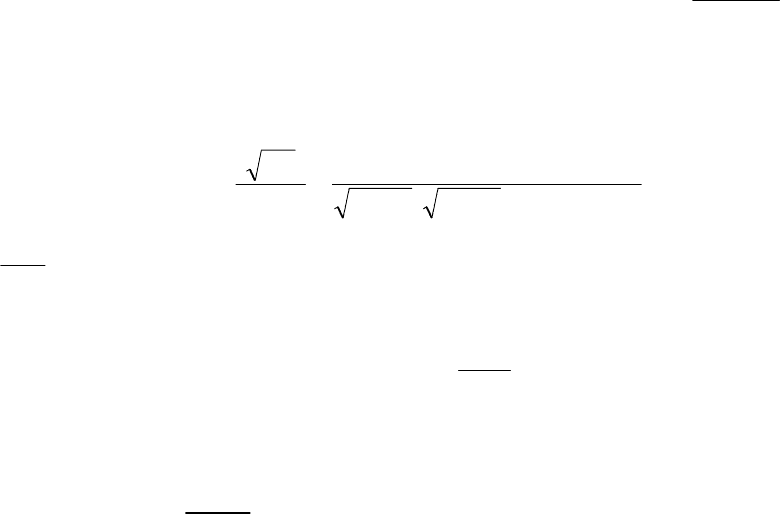
66
Пусть входное воздействие g(t) представляется реализацией
случайного процесса с энергетическим спектром
G
ag
a
g
()ω
σ
ω
=
+
2
2
22
и в
сумме z(t)=g(t)+n(t) с белым шумом (помехой) n(t) поступает на
систему управления. В соответствии с методом Винера оптималь-
ная реализуемая система имеет передаточную функцию
Wj
N
j
q
qq jT
P
()
()
()()
ω
ψω
ω
=− =
++++
1
2
12 12 11
0
,
где
q
Na
g
=
σ
2
0
, x(jω)=W
P
(jω)Z(jω).
Р.Калман предложил другое представление того же решения
в виде дифференциального уравнения
dx t
dt
ax t VN z t x t
()
() (() ())=− + −
−
0
1
.
При этом входное воздействие g(t) удобно представить в виде
выходного сигнала фильтра (рис.38), описываемого дифференци-
альным уравнением
()
() ()
dg t
ag t t
dt
ξ
=− +
.
Фильтр, с помощью которого моделируется входное воздей-
ствие g(t), обычно называют
формирующим фильтром. Само же
входное воздействие g(t) при этом является состоянием форми-
рующей системы.
Было установлено, что при описании входных сигналов в ви-
де состояния некоторой системы всегда получается решение в виде
точно такой же по виду системы с обратной связью. При этом
структура САУ сохраняется для любого интервала времени, в том
числе
и во время переходного процесса, при изменении коэффици-
ентов
aN
g
,,
0
2
σ
во времени, а также в случае, когда x(t) является век-
тором, т.е. при одновременном управлении по нескольким пара-
метрам. И во всех этих случаях структура системы управления ока-
зывается оптимальной в смысле минимума дисперсии ошибки
{}
σ
0
22
() () ())tMxtgt=−
.
В этом разделе вначале рассматриваются математические мо-
дели входных многомерных нестационарных воздействий. После
этого обсуждается структура оптимальной многомерной системы,
которая называется фильтром Калмана.
+
67
Описание входных воздействий
Пусть нам необходимо осуществлять управление одновре-
менно n выходными сигналами системы
xt xt
n1
( ),..., ( ). При этом мы
хотим получить наименьшие отличия этих сигналов от заданных
функций – входных воздействий
gt
gt
gt
n
()
()
...
()
=
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
1
. Будем описывать
входные воздействия с помощью системы линейных дифференци-
альных уравнений состояния:
dg t
dt
Atgt Vt t
()
() () () ()=+ξ
,
где A(t) – (n
× n) – матрица:
at at
at at
at at
n
n
nnn
11 1
21 2
1
() ... ()
() ... ()
... ... ...
() ... ()
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
; ξ
ξ
ξ
()
()
...
()
t
t
t
m
=
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
1
– век-
торный белый шум с энергетическим спектром каждой компоненты
NtNt N t
m
ξξ ξ
12
(), (),..., () соответственно.
V(t) - (n
× m)-матрица V(t)=
vt vt
vt vt
vt vt
n
n
nnn
11 1
21 2
1
() ... ()
() ... ()
... ... ...
() ... ()
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
.
Рассмотрим примеры.
Пример 1. Уравнение состояния для трех независимых пара-
метров.
Предположим, что необходимо обеспечить измерение траек-
тории по 3 координатам, не связанным друг с другом. Эти коорди-
наты описываются случайными процессами, соответствующими
дифференциальным уравнениям:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
+−=
+−=
+−=
).t()t(g)t(a
dt
)t(dg
),t()t(g)t(a
dt
)t(dg
),t()t(g)t(a
dt
)t(dg
333
3
222
2
111
1
ξ
ξ
ξ

68
Введем вектор
gt
gt
gt
gt
()
()
()
()
=
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
1
2
3
, матрицу
At
at
at
at
()
()
()
()
=
−
−
−
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
1
2
3
00
00
00
и
белый шум
ξ
ξ
ξ
ξ
()
()
()
()
t
t
t
t
=
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
1
2
3
. Тогда одновекторное уравнение состояния
dg t
dt
At gt t
()
() () ()=+ξ
в точности описывает все заданные входные воз-
действия Для проверки достаточно раскрыть в этом уравнении мат-
ричные и векторные обозначения.
Пример 2. Входное воздействие с дробно-рациональным
энергетическим спектром.
Пусть g(t) описывается дифференциальным уравнением ви-
да:
dgt
dt
a
dgt
dt
a
dg t
dt
agt t
3
3
1
2
2
23
() () ()
() ()+++=ξ
.
Найдем энергетический спектр такого воздействия. Для этого
вначале выполним преобразование Лапласа
pgpapgpapgpagp p
3
1
2
23
() () () () ()+++=ξ
и запишем передаточную функ-
цию формирующего фильтра
Hp
papapa
ϕ
()=
+++
1
3
1
2
23
.
Энергетический спектр входного воздействия находится по форму-
ле
() ( )
2
gg
GHjN
ξ
ωω
= . При выборе различных коэффици-
ентов
aaa
123
,, могут быть получены энергетические спектры разно-
образной формы. Но рассматриваемое уравнение имеет третий по-
рядок. Преобразуем его в одно векторное уравнение. Введем вспо-
могательные переменные:
dgt
dt
gt
dg t
dt
gt
2
2
21
()
(),
()
()==
. Тогда исходное
уравнение перепишется в форме:
dg t
dt
ag t ag t agt t
dg t
dt
gt
dg t
dt
gt
2
12 21 3
1
2
1
()
() () () ()
()
()
()
()
=− − − +
=
=
⎧
⎨
⎪
⎪
⎪
⎩
⎪
⎪
⎪
ξ
.
69
Введем теперь вектор
gt
gt
gt
gt
()
()
()
()
=
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
2
1
и тогда
dg
dt
aaa
gt t=
−−−
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
+
123
100
010
() ()ξ
, где
ξ
ξ
()
()
;t
t
A
aaa
=
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
=
−
−−
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
0
0
100
010
123
. Таким
образом дифференциальное уравнение третьего порядка удается
преобразовать к стандартной векторной форме. Очевидно, что точ-
но так же к векторному уравнению первого порядка можно преоб-
разовать дифференциальное уравнение произвольного порядка.
Пример 3. Полиномиальное воздействие.
Пусть
2
0
() 2gt g Vt at=++ . Такой входной сигнал получается
как решение следующего дифференциального уравнения
dg
dt
3
3
0= .
Заметим, что этот результат можно рассматривать как частный слу-
чай предыдущего примера, полагая
aaa
123
0
=
=
=
≡
ξ
. Тогда
dg
dt
3
3
0=
,
2
2
00
2
,,()2,,,
dg dg
aatV
g
tVtat
g
aV
g
dt dt
==+ =++
– начальные
условия.
Введем вспомогательные переменные
dgt
dt
gt
dg t
dt
gt
2
2
21
()
(),
()
()==
.
Тогда уравнения состояния запишутся в виде:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=
=
=
),t(g
dt
)t(dg
),t(g
dt
)t(dg
,0
dt
)t(dg
1
2
1
2
или в стандартной форме:
dg
dt
Ag t t=+() ()ξ
,
где
A =
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
000
100
010
,
ξ()t =
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
0
0
0
.
70
Таким образом, исходное дифференциальное уравнение со-
стояния
dg
dt
At gt t=+() () ()ξ
описывает широкий класс реальных слу-
чайных процессов.
Пусть теперь
gt() передается по каналу связи и вместе с по-
мехой поступает на вход системы управления:
Zt Ctgt nt() () () ()=+, где
Zt
zt
zt
m
()
()
...
()
=
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
1
, C(t)=
ct ct
ct ct
ct ct
n
n
mmn
11 1
21 2
1
() ... ()
( ) ... ( )
... ... ...
( ) ... ( )
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
;
nt()=
nt
nt
m
1
()
...
()
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
– помеха в виде векторного белого шума со спектраль-
ными плотностями каждой компоненты
01 02 0
( ), ( ),..., ( )
m
NtNt N t со-
ответственно.
Рассмотренная векторная модель позволяет дать математиче-
ское описание различных ситуаций, возникающих при формирова-
нии входных сигналов проектируемых САУ.
Пример 4. Предположим, что один и тот же входной сигнал
g(t) передается по двум независимым каналам связи. При этом на
выходе первого канала наблюдается смесь
(
)()()
(
)
11 1
zt ctgt nt
=
+
сигнала
()
gt с помехой
(
)
1
nt, а на выходе второго канала наблюда-
ется процесс
() ()
(
)
(
)
22 2
zt ctgt nt=+. Для того, чтобы представить
такие наблюдения в стандартной векторной форме, введем векторы
() () ()
()
() () ()
(
)
12 1 2
,
TT
zt z t z t nt n t n t== и матрицу
()
()
()
1
2
ct
ct
ct
⎛⎞
=
⎜⎟
⎝⎠
. В этом случае одно векторное уравнение
() () ()
(
)
zt ctgt nt=+
или
(
)
()
(
)
()
()
()
()
11 1
22 2
zt ct nt
gt
zt ct nt
⎛⎞⎛⎞ ⎛⎞
=+
⎜⎟⎜⎟ ⎜⎟
⎝⎠⎝⎠ ⎝⎠
описыва-
ет двухканальную систему наблюдений скалярного процесса
(
)
gt.
Пример 5. Пусть входной сигнал
(
)
gt имеет сложный энер-
гетический спектр и описывается дифференциальным уравнением
третьего порядка (см. пример 2). В этом случае уравнение состоя-
