Васильев А., Михайлин В. Введение в спектроскопию диэлектриков
Подождите немного. Документ загружается.

ïðåîáðàçîâàíèÿ Ôóðüå (ÁÏÔ), òî ïîòðåáóåòñÿ òîëüêî
NNln
óìíî-
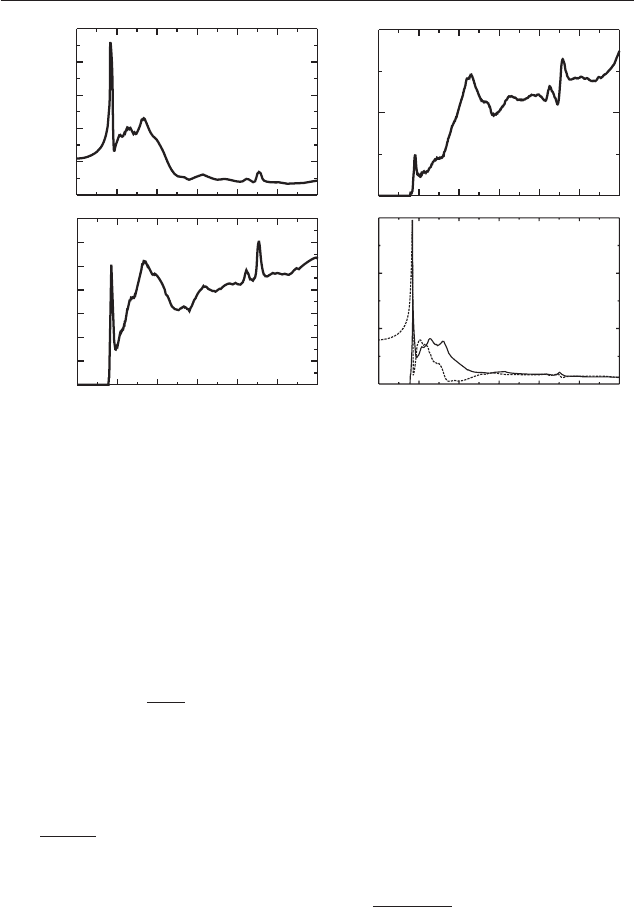
æåíèé. Ïðèìåð èñïîëüçîâàíèÿ òàêîãî ïîäõîäà ê ðàñ÷åòó îïòè÷åñêèõ
ôóíêöèé ïðèâåäåí íà ðèñ. 5.
Äèñïåðñèîííûå ñîîòíîøåíèÿ (1.21) è (1.22) ïîçâîëÿþò ïîëó-
÷èòü ðÿä èíòåðåñíûõ èíòåãðàëüíûõ ñîîòíîøåíèé (ñì., íàïðèìåð,
Altarelli et al, 1972). Êàê óæå áûëî îòìå÷åíî âûøå,
ε
2
íà áîëüøèõ
÷àñòîòàõ ñòðåìèòñÿ ê íóëþ, è ïîýòîìó ìîæíî çàïèñàòü
() ()
εω
πω
ε
1
2
2
0
1
2
−=−
∞
∫
xxdx
ïðè
ω→∞
. (1.28)
Ñðàâíåíèå (1.28) ñ ñîîòíîøåíèåì (1.27) äàåò ïðàâèëî ñóìì â ñëåäó-
þùåé ôîðìå:
() ()
m
e
dfdN
2
22
2
00
π
ωεωω ωω
∞∞
∫∫
≡=
. (1.29)
Çäåñü ââåäåíà ñèëà îñöèëëÿòîðîâ
()
()
f
m
e
dω
ωε ω
π
ω≡
2
22
2
, ïðèõîäÿùèõñÿ
íà èíòåðâàë ÷àñòîò
dω
. Ïðàâèëî ñóìì (1.29) âûðàæàåò òîò ôàêò, ÷òî
ñóììà âñåõ ñèë îñöèëëÿòîðîâ â åäèíèöå îáúåìà ðàâíà ÷èñëó ýëåêòðî-
íîâ â åäèíèöå îáúåìà. Èíòåãðàë â (1.29) äîëæåí áûòü ñõîäÿùèìñÿ,
îòêóäà ñëåäóåò, ÷òî
()
εω
2
ïðè áîëüøèõ ÷àñòîòàõ ïàäàåò ñ ðîñòîì
32 Ãëàâà 1. Âçàèìîäåéñòâèå ýëåêòðîìàãíèòíîãî ïîëÿ ñ òâåðäûì òåëîì
0 5 10 15 20 25 30
1,4 10×
6
1,0 10×
6
1,0 10×
6
8×10
5
6×10
5
4×10
5
2×10
5
0
-1
Ïîãëîùåíèå, ñì
0
0,5
1,0
Ýíåðãèÿ ôîòîíà, ýÂ
0
5
10
15
PbWO
4
10
0
20
30
40
50
Îòðàæåíèå, %
0 5 10 15 20 25 30
0 5 10 15 20 25 30
0 5 10 15 20 25 30
Ýíåðãèÿ ôîòîíà, ýÂ
Im(-1/ )ε
εε,
12
Ðèñ. 5. Ñïåêòð îòðàæåíèÿ âîëüôðàìàòà ñâèíöà [????] è ïåðåñ÷èòàííûå ñ
èñïîëüçîâàíèåì ÁÏÔ îïòè÷åñêèå ôóíêöèè.

ω
ω
áûñòðåå, ÷åì
ω
−2
.
 äðóãîì ïðåäåëå
ω→0
äëÿ äèýëåêòðèêîâ (
σ=0
) ìîæíî ïîëó-
÷èòü:
()
()
ε
π
εω
ω
ω
π
ω
1
2
0
2
2
01
24
−= ≡
∞
−
∫
d
eN
m
, (1.30)
ãäå ÷åðòà îçíà÷àåò óñðåäíåíèå ñ ïîìîùüþ ñèëû îñöèëëÿòîðîâ:
()
ω
ω
ωω
−
∞
≡
∫
2
2
0
11
N
fd
.
 óðàâíåíèè (1.30)
()
ε
1
0
- ñòàòè÷åñêàÿ äèýëåêòðè÷åñêàÿ ïðîíèöàå-
ìîñòü, îáû÷íî îáîçíà÷àåìàÿ êàê
ε
0
. Íåîáõîäèìî îáðàòèòü âíèìàíèå
íà òî, ÷òî èíòåãðèðîâàíèå â (1.30) ïðîèçâîäèòñÿ ïî âñåìó äèàïàçîíó
÷àñòîò, â òîì ÷èñëå è ïî îáëàñòè ïîãëîùåíèÿ â ÈÊ-äèàïàçîíå ñ ó÷àñ-
òèåì ôîíîíîâ. Âîîáùå ãîâîðÿ, â îòëè÷èå îò ôîðìóëû (1.30), êîòîðàÿ
÷óâñòâèòåëüíà ê ïîâåäåíèþ
()
εω
2
ïðè ñðàâíèòåëüíî íèçêèõ ÷àñòîòàõ,
ïðàâèëî ñóìì (1.29) â îñíîâíîì îïðåäåëÿåòñÿ ïîâåäåíèåì
()
εω
2
ïðè
âûñîêèõ ÷àñòîòàõ. Îöåíêà òî÷íîñòè ðàñ÷åòà ïî ïðàâèëàì Êðàìåð-
ñà—Êðîíèãà ñ ïîìîùüþ ýòèõ ïðàâèë ñóìì ïîìîãàåò âûáðàòü àïïðîê-
ñèìàöèþ äëÿ âûñîêî- è íèçêî÷àñòîòíûõ ÷àñòîòíûõ äèàïàçîíîâ.
Ïðè àíàëèçå îïòè÷åñêèõ ôóíêöèé ñ ïîìîùüþ ïðàâèë ñóìì ÷àñòî
ââîäèòñÿ ýôôåêòèâíîå ÷èñëî ýëåêòðîíîâ
()
N
eff
ω
è ýôôåêòèâíàÿ ñòà-
òè÷åñêàÿ äèýëåêòðè÷åñêàÿ ïðîíèöàåìîñòü
()
εω
eff
0
. Îíè ïîëó÷àþòñÿ ïî
ôîðìóëàì (1.29) è (1.30), â êîòîðûõ âåðõíèé ïðåäåë èíòåãðèðîâà-
íèÿ çàìåíåí íà ÷àñòîòó
ω
. Ýòè äâå ôóíêöèè èíòåðïðåòèðóþòñÿ êàê
÷èñëî ýëåêòðîíîâ, ó÷àñòâóþùèõ â ïåðåõîäàõ â äèàïàçîíå ÷àñòîò îò 0
äî
ω
è êàê âêëàä òàêèõ ýëåêòðîíîâ â
ε
0
. Áûñòðûé ñòóïåí÷àòûé ðîñò
òàêèõ ôóíêöèé óêàçûâàåò íà íà÷àëî ïåðåõîäîâ èç âñå áîëåå ãëóáîêèõ
îáîëî÷åê. Ê ñîæàëåíèþ, òî÷íîå îïðåäåëåíèå òàêèõ ôóíêöèé îêàçû-
âàåòñÿ íåâîçìîæíûì. Áîëåå òîãî, îíè êðàéíå ÷óâñòâèòåëüíû (îñîáåí-
íî
()
N
eff
ω
) ê îøèáêàì ïîäãîíêè ïðè âû÷èñëåíèè ïðåîáðàçîâàíèé
Êðàìåðñà—Êðîíèãà.
Ïðàâèëà ñóìì, àíàëîãè÷íûå ñîîòíîøåíèÿì (1.29) è (1.30), ìîæ-
íî çàïèñàòü è äëÿ
()
n ω
è
()
κω
, à òàêæå äëÿ äðóãèõ îïòè÷åñêèõ ôóíêöèé
(íàïðèìåð, èñïîëüçóåìîé íèæå ôóíêöèè ïîòåðü ýíåðãèè
()
Im −
1
εω
).
§ 1. Ôåíîìåíîëîãè÷åñêîå îïèñàíèå âçàèìîäåéñòâèÿ ñâåòà ñ âåùåñòâîì 33

§ 2 Õàðàêòåðèñòè÷åñêèå ïîòåðè ýíåðãèè
ýëåêòðîíîâ
Ïðè ïðîõîæäåíèè ÷åðåç âåùåñòâî çàðÿæåííàÿ ÷àñòèöà èíòåíñèâ-
íî âçàèìîäåéñòâóåò ñî âñåìè âîçìîæíûìè âîçáóæäåíèÿìè. Ðàññìàò-
ðèâàÿ òîëüêî ýëåêòðîñòàòè÷åñêîå âçàèìîäåéñòâèå ÷åðåç ïðîäîëüíîå
ýëåêòðè÷åñêîå ïîëå, íåîáõîäèìî ó÷èòûâàòü ïîëÿðèçàöèþ âåùåñòâà
(ñì., íàïð. Neufeld, Ritchie, 1965, Vager, Gemmel, 1976, Êàëàøíèêîâ
è äð., 1980). Ìîæíî ïîêàçàòü, ÷òî ïîòåðè ýíåðãèè ýëåêòðîíà íà ñîç-
äàíèå âîçáóæäåíèÿ ñ èìïóëüñîì
hq
è ýíåðãèåé
hω
ïðîïîðöèîíàëüíû
()
()
()
Im
~
,
,
~
,
−
=
1
2
2
εω
εω
εω
q
q
q
. (2.1)
Âîîáùå ãîâîðÿ,
()
~
,εωq
â ýòîé ôîðìóëå äîëæíà ñîîòâåòñòâîâàòü ïðî-
äîëüíîé, à íå ïîïåðå÷íîé ÷àñòè òåíçîðà äèýëåêòðè÷åñêîé ïðîíèöàå-
ìîñòè (áîëåå ïîäðîáíî ðàçëè÷èå ìåæäó ýòèìè äâóìÿ òåíçîðàìè ðàññ-
ìàòðèâàåòñÿ â ñëåäóþùåé ãëàâå). Ôîðìóëà (2.1) ñâÿçàíà ñ íàëè÷èåì
~
ε
−1
â âûðàæåíèè (1.6) äëÿ ïðîäîëüíîãî ýëåêòðè÷åñêîãî ïîëÿ
E
l
.
Ýëåêòðîí (èëè äðóãàÿ çàðÿæåííàÿ ÷àñòèöà) ñîçäàåò â êðèñòàëëå ïîëå
ñ ïîòåíöèàëîì
ϕε()
$
rer=−
, ãäå
$
ε
- îïåðàòîð äèýëåêòðè÷åñêîé ïðîíè-
öàåìîñòè. Ôóðüå-êîìïîíåíòà ýòîãî ïîëÿ èìååò âèä
()
4
2
πεωeq
~
,q
, ãäå
()
~
,εωq
- ôóðüå îáðàç îïðåàòîðà äèýëåêòðè÷åñêîé ïðîíèöàåìîñòè ïî
ïðîñòðàíñòâåííûì êîîðäèíàòàì è âðåìåíè. Äëÿ îöåíêè ïîòåðü ýíåð-
ãèè ýëåêòðîíà â ôîðìóëå (2.1) ìîæíî ïîëîæèòü
q = 0
è ïðîèíòåãðè-
ðîâàòü ïî âñåì ÷àñòîòàì:
()
−−
∫
dE
dx
d~Im
~
ω
εω
1
.
Ðàññìîòðèì áîëåå ïîäðîáíî ñâîéñòâà ôóíêöèè
()
()
Im
~
−
−
εω
1
. Âî-
ïåðâûõ, ñîãëàñíî (2.1), ïîòåðè ýíåðãèè êâàíòàìè
hω
îòëè÷íû îò íóëÿ
â äâóõ ñëó÷àÿõ. Åñëè
()
εω
2
0≠
, òî âîçáóæäàþòñÿ òàêèå ýëåêòðîííûå
ñîñòîÿíèÿ, êîòîðûå äàþò âêëàä â
()
εω
2
íà ñîîòâåòñòâóþùåé ÷àñòîòå.
Òåì ñàìûì ïîòåðè ýíåðãèè ïðèâîäÿò ê ðîæäåíèþ íîâûõ ýëåêòðîííûõ
âîçáóæäåíèé. Ïðàâäà, âêëàä ðàçíûõ ñîñòîÿíèé ìåíÿåòñÿ â ñèëó

èçìåíåíèÿ
()
1
2
~
εω
ñ ÷àñòîòîé.  ÷àñòíîñòè, îí âîçðàñòàåò ñ óìåíüøå-
íèåì
()
~
εω
2
. Íàèáîëåå èíòåðåñíûé âêëàä â ïîòåðè ýíåðãèè âîçìîæåí
è ïðè
()
εω
2
0=
. Åñëè îïðåäåëèòü
ω
pl
êàê êîðåíü óðàâíåíèÿ
()
εω
1
0
pl
=
,òî
()
()
()()[]
εω
εω
πω
δω−ω δω ω
2
2
~
≈−+
pl
pl pl
2
.
×àñòîòà, íà êîòîðîé
ε
1
îáðàùàåòñÿ â íîëü, íàçûâàåòñÿ ïëàçìåí-
íîé ÷àñòîòîé. Ïðè ýòîì âîçáóæäàþòñÿ îñîáûå êâàçè÷àñòèöû - ïëàç-
ìîíû, ÿâëÿþùèåñÿ ïðîäîëüíûìè êîëåáàíèÿìè ýëåêòðè÷åñêîãî ïîëÿ.
Ñëó÷àé
()
εω
2
0=
ñîîòâåòñòâóåò ìîäåëè ñâîáîäíûõ ýëåêòðîíîâ. Ïðè
ýòîì
()
εω
π
ω
=−1
4
2
2
Ne
m
, (2.2)
ãäå
N
- êîíöåíòðàöèÿ è
m
- ìàññà ñâîáîäíûõ ýëåêòðîíîâ. Èç (2.2) ïî-
ëó÷àåì
ω
π
pl
=
4
2
Ne
m
. (2.3)
Åñëè ïîãëîùåíèå îòëè÷íî îò íóëÿ,
()
εω
2
0≠
, òî âñå ðàâíî íà
áîëüøèõ ÷àñòîòàõ
()
εω
2
0→
. Â ýòîé îáëàñòè ñîîòíîøåíèå (2.2) ñâÿçà-
íî ñ ïðàâèëàìè ñóìì, ñëåäóþùèìè èç äèñïåðñèîííûõ ñîîòíîøåíèé
Êðàìåðñà—Êðîíèíãà (1.24).  êà÷åñòâå
N
çäåñü ñòîèò ïëîòíîñòü âà-
ëåíòíûõ ýëåêòðîíîâ, ïåðåõîäû ñ êî-
òîðûõ ê
ω
pl
óæå èñ÷åðïàíû. Îäíàêî
â áîëüøèíñòâå ñëó÷àåâ âûðàæåíèå
äëÿ
ω
pl
(2.3) ïðåäñòàâëÿåò ñîáîé
ëèøü ãðóáóþ îöåíêó. Äàæå â ìåòàë-
ëàõ ýòî ñîîòíîøåíèå â áîëüøèíñòâå
ñëó÷àåâ íå ïðèìåíèìî.  äåéñòâè-
òåëüíîñòè ïëàçìåííóþ ÷àñòîòó íåîá-
õîäèìî îïðåäåëÿòü èç óñëîâèÿ
()
εω
1
0
pl
=
. Â ñèëó êîìïëåêñíîñòè
~
ε
âûðàæåíèå äëÿ ïëàçìåííîé ÷àñòîòû
òàêæå ïîëó÷àåòñÿ êîìïëåêñíûì, ïðè-
÷åì ìíèìàÿ ÷àñòü
~
ω
pl
ðàñòåò ñ ðîñòîì
()
εω
2
Re
pl
. Òåì ñàìûì ïëàçìîíû ñòà-
íîâÿòñÿ êîðîòêîæèâóùèìè. Â áîëü-
øèíñòâå äèýëåêòðèêîâ ìàêñèìóì íà
§ 2. Õàðàêòåðèñòè÷åñêèå ïîòåðè ýíåðãèè ýëåêòðîíîâ 35
1,0
0,6
0,2
01020
-Im
ν
1
_
ε
h
,
eV
Ðèñ. 6. Ñïåêòð õàðàêòåðèñòè÷åñ-
êèõ ïîòåðü äëÿ Ge (Philipp,
Ehrenrich, 1963)
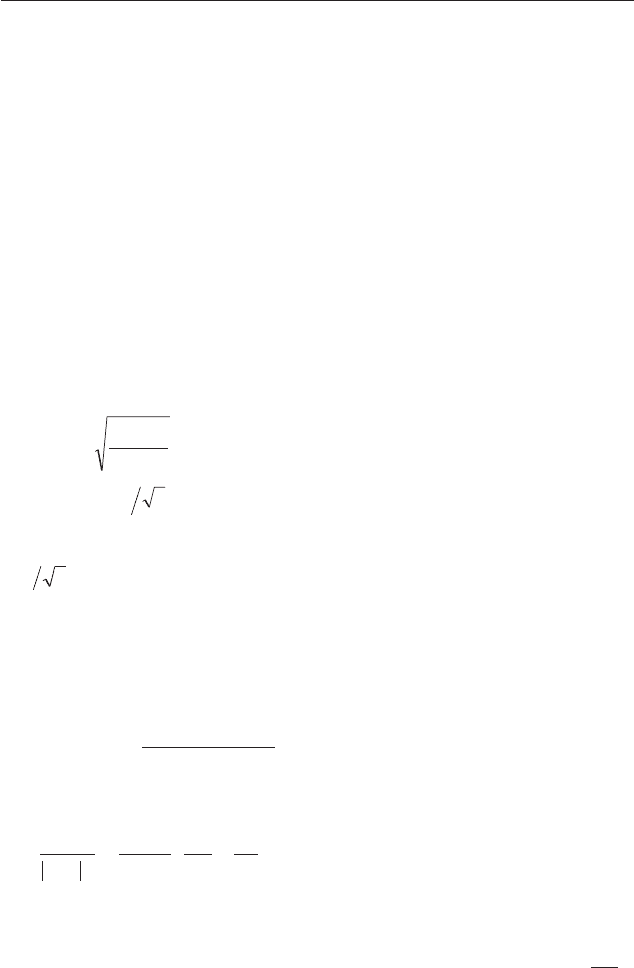
÷àñòîòå
ω
pl
èìååò ïîëóøèðèíó ïîðÿäêà íåñêîëüêèõ ýëåêòðîí-âîëüò
(ñì., íàïðèìåð, ðèñ. 4–6), ò.å. âðåìÿ æèçíè ïëàçìîíà ïîðÿäêà
10
15−
ñ. Òîëüêî â ìåòàëëàõ ïëàçìîí ÿâëÿåòñÿ îòíîñèòåëüíî äîëãîæèâóùèì
âîçáóæäåíèåì, è èìåííî òàì îí íàèáîëåå äîñòîâåðíî îïðåäåëÿåòñÿ
÷åðåç õàðàêòåðèñòè÷åñêèå ïîòåðè ýëåêòðîíîâ.
Íà ïðèìåðå ïëàçìîíà ìîæíî íàèáîëåå ïðîñòî îöåíèòü âëèÿíèå
ïîâåðõíîñòè íà âîçáóæäåíèÿ â òâåðäîì òåëå, ïîñêîëüêó åå âëèÿíèå
íà äðóãèå ýëåêòðîííûå âîçáóæäåíèÿ (îáðàçîâàíèå òàììîâñêèõ ñîñòî-
ÿíèé) îöåíèòü ìîæíî ëèøü íà óðîâíå ìèêðîñêîïè÷åñêîé òåîðèè. Äëÿ
ïëàçìåííûõ âîëí â äèýëåêòðèêå, îãðàíè÷åííîì ïëîñêîñòüþ è çàíè-
ìàþùåì ïîëóïðîñòðàíñòâî, óðàâíåíèå äëÿ ÷àñòîòû ïðîäîëüíûõ âîëí
èìååò âèä
()
~
εω
ps
+=10
. (2.4)
B ðàìêàõ ïðèáëèæåíèé, äëÿ êîòîðûõ ïîëó÷åíî âûðàæåíèå (2.3),
èìååì (ñì., íàïð. Ritchie, 1957)
ω
π
ps
=
2
2
Ne
m
,
ò. å.
ωω
ps
pl
2=
.  ñëó÷àå æå, êîãäà àñèìïòîòèêà (2.2) âáëèçè
ω
ps
íå ðàáîòàåò, íåîáõîäèìî ïîëüçîâàòüñÿ òî÷íûì óðàâíåíèåì (2.4), à
îòíîøåíèå ÷àñòîò ïîâåðõíîñòíûõ è îáúåìíûõ ïëàçìîíîâ îòëè÷àåòñÿ
îò
12
.
Ôóíêöèÿ
()
εω
ìîæåò îáðàùàòüñÿ â íîëü íå òîëüêî â îáëàñòè ýíåð-
ãèé ýëåêòðîííûõ ïåðåõîäîâ, íî è â îáëàñòè ôîíîííûõ êîëåáàíèé ðå-
øåòêè.  ïåðâîì ïðèáëèæåíèè â ôîíîííîé îáëàñòè äèýëåêòðè÷åñêàÿ
ïðîíèöàåìîñòü èîííûõ êðèñòàëëîâ èìååò âèä (ñì., íàïðèìåð, Äàâû-
äîâ, 1976, à òàêæå ÷àñòü 3 äàííîé êíèãè):
()
()
εω ε
εε
ω
=+
−
−
∞
∞0
2
Ω
Ω
TO
2
TO
2
. (2.5)
Ïðè ýòîì
()
()
()()
[]
εω
εω
π
εε
δω− δω
2
2
0
11
~
≈−
−+
∞
Ω
ΩΩ
LO
LO LO
2
,
ãäå
ε
0
- ñòàòè÷åñêàÿ è
ε
∞
- âûñîêî÷àñòîòíàÿ äèýëåêòðè÷åñêèå ïðîíè-
öàåìîñòè,
Ω
LO
- ÷àñòîòà ïðîäîëüíîãî, à
Ω
TO
- ïîïåðå÷íîãî îïòè÷åñêî-
ãî ôîíîíà, ñâÿçàííûå ìåæäó ñîáîé ñîîòíîøåíèåì
ΩΩ
LO TO
22
0
=
∞
ε
ε
.
×àñòîòà
Ω
TO
ñîîòâåòñòâóåò ïîëþñó äèýëåêòðè÷åñêîé ïðîíèöàåìîñòè
36 Ãëàâà 1. Âçàèìîäåéñòâèå ýëåêòðîìàãíèòíîãî ïîëÿ ñ òâåðäûì òåëîì

(2.5), à
Ω
LO
- íóëþ ýòîé ôóíêöèè.
Ôóíêöèÿ ïîòåðü ýíåðãèè ýëåêòðîíà ïîêàçûâàåò â ýòîì ñëó÷àå íà
èñïóñêàíèå è ïîãëîùåíèå ïðîäîëüíûõ îïòè÷åñêèõ ôîíîíîâ. Òàêèì
îáðàçîì, áûñòðûé ýëåêòðîí ïðè ïðîõîæäåíèè ÷åðåç âåùåñòâî òåðÿåò
ñâîþ ýíåðãèþ íà ñîçäàíèå âñåãî êîìïëåêñà ýëåìåíòàðíûõ âîçáóæäå-
íèé, âçàèìîäåéñòâóþùèõ ñ ýëåêòðîíîì ÷åðåç ïðîäîëüíîå ýëåêòðè÷åñ-
êîå ïîëå: ïðîäîëüíûõ îïòè÷åñêèõ ôîíîíîâ, ýëåêòðîííî-äûðî÷íûõ
âîçáóæäåíèé è ïëàçìîíîâ. Ïðîâåäåííîå âûøå ðàññìîòðåíèå áûëî
ñïðàâåäëèâî äëÿ ýëåêòðîíîâ äîñòàòî÷íî âûñîêèõ ýíåðãèé, òàêèõ, ÷òî
èñïóñêàíèå âîçáóæäåíèÿ ñ ýíåðãèåé â íåñêîëüêî ýëåêòðîí-âîëüò íåç-
íà÷èòåëüíî ìåíÿëî èìïóëüñ âîçáóæäåíèÿ. Äëÿ ðàññåÿíèÿ áîëåå íèç-
êîýíåðãåòè÷íûõ ýëåêòðîíîâ íåîáõîäèìî ó÷èòûâàòü ðîæäåíèå íå
òîëüêî äëèííîâîëíîâûõ âîçáóæäåíèé, íî è êîðîòêîâîëíîâûõ, ïîýòî-
ìó ôóíêöèÿ ïîòåðü óæå íå âûðàæàåòñÿ ÷åðåç
()
~
εω
, à ëèøü ÷åðåç
()
~
,εωq
. Ïîäðîáíî âñå ýòè ïðîöåññû ðàññìîòðåíû â ïàðàãðàôå 4.13.
§ 2. Õàðàêòåðèñòè÷åñêèå ïîòåðè ýíåðãèè ýëåêòðîíîâ 37

§ 3 Ìèêðîñêîïè÷åñêîå îïèñàíèå âçàèìîäåéñòâèÿ
ñâåòà ñ âåùåñòâîì
3.1 Äèýëåêòðè÷åñêàÿ ïðîíèöàåìîñòü
Âçàèìîäåéñòâèå ñâåòà ñ âåùåñòâîì îïèñûâàåòñÿ îáû÷íî â ïîëóê-
ëàññè÷åñêîì ïðèáëèæåíèè. Ïîäðîáíîå îïèñàíèå ýòèõ ïðîöåññîâ
ìîæíî íàéòè â ðÿäå êíèã (Pines (1963), Pines, Nozieres (1966),
Platzman, Wolf (1973)). Çäåñü ìû ââåäåì îñíîâíûå ïîíÿòèÿ, êàñàþ-
ùèåñÿ ýòîãî âçàèìîäåéñòâèÿ.  ïîëóêëàññè÷åñêîì ïðèáëèæåíèè ãà-
ìèëüòîíèàí ñèñòåìû «ýëåêòðîìàãíèòíîå ïîëå ïëþñ òâåðäîå òåëî» ìî-
æåò áûòü ðàçáèò íà ñóììó òðåõ ñëàãàåìûõ:
$$ $ $
int
HH H H=++
0R
, (3.1)
ãäå
$
H
0
— ãàìèëüòîíèàí, îïèñûâàþùèé òâåðäîå òåëî áåç èçëó÷åíèÿ,
$
H
R
— ãàìèëüòîíèàí ñâîáîäíîãî ýëåêòðîìàãíèòíîãî ïîëÿ,
$
int
H
—
÷ëåí, îïèñûâàþùèé âçàèìîäåéñòâèå ñâåòà ñ âåùåñòâîì. Ïîëóêëàññè-
÷åñêîå îïèñàíèå ïðåäóñìàòðèâàåò, âî-ïåðâûõ, êâàçèêëàññè÷åñêîå
îïèñàíèå ïîëÿ èçëó÷åíèÿ. Âî-âòîðûõ, ÷ëåí
$
int
H
ðàññìàòðèâàåòñÿ
ëèøü êàê âîçìóùåíèå. Ïðè òàêîì îïèñàíèè îïóñêàþòñÿ ýôôåêòû îá-
ðàçîâàíèÿ ïîëÿðèòîíîâ ðàçíîãî òèïà — ñîñòîÿíèé, ïðåäñòàâëÿþùèõ
ñîáîé ñìåñü ýëåêòðîííûõ èëè ôîíîííûõ âîçáóæäåíèé ñ ôîòîíàìè.
Âçàèìîäåéñòâèå ïîäîáíîãî òèïà íà ïðèìåðå ýêñèòîííîãî ïîëÿðèòîíà
áóäåò ðàçîáðàíî â §8.
Ñîãëàñíî òåì æå ïîëóêëàññè÷åñêèì ïðåäñòàâëåíèÿì äëÿ âû÷èñ-
ëåíèÿ
$
int
H
ïîñòóïàþò ñëåäóþùèì îáðàçîì. Ýëåêòðîìàãíèòíîå ïîëå
ðàññìàòðèâàåòñÿ êàê âíåøíÿÿ ñèñòåìà, ïîýòîìó ÷ëåí
$
H
R
â (3.1) îïóñ-
êàåòñÿ. Ïðè ïîìåùåíèè òâåðäîãî òåëà â ýëåêòðîìàãíèòíîå ïîëå â ãà-
ìèëüòîíèàíå, îïèñûâàþùåì òâåðäîå òåëî, ïðîèñõîäèò çàìåíà îïåðà-
òîðîâ èìïóëüñà âñåõ ÷àñòèö
$
p
i
íà îïåðàòîðû îáîáùåííîãî èìïóëüñà
$
$
()P
ii
i
i
e
c
=+pAr
, ãäå
Ar(,)t
— âåêòîð-ïîòåíöèàë ýëåêòðîìàãíèòíîãî
ïîëÿ,
e
i
è
ã
i
- çàðÿä è êîîðäèíàòû
i
-é ÷àñòèöû.  íåðåëÿòèâèñòñêîì
ïðèáëèæåíèè îáîáùåííûå èìïóëüñû âõîäÿò â ãàìèëüòîíèàí â âèäå
ñóììû êèíåòè÷åñêèõ ýíåðãèé ÷àñòèö:
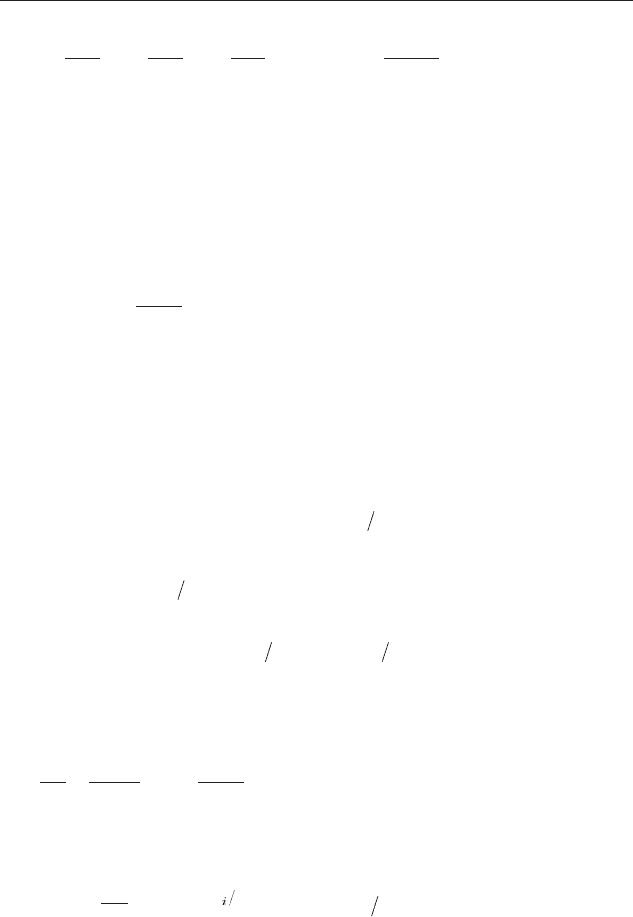
$
$
()
$
()
p
Ar A r
i
i
i
i
i
i
i
i
ii
i
i
i
i
mm
e
mc
e
mc
22 2
2
2
22
2
∑∑∑
=− +
P
P
i
∑
. (3.2)
Ïðè âû÷èñëåíèè âòîðîãî ÷ëåíà ó÷òåíî, ÷òî äëÿ ïîïåðå÷íîéýëåêòðî-
ìàãíèòíîé âîëíû
divA = 0
, è ïîýòîìó
Ar()
i
è
$
P
i
êîììóòèðóþò äðóã ñ
äðóãîì.  ñëó÷àå îòíîñèòåëüíî ñëàáûõ èíòåíñèâíîñòåé ýëåêòðîìàã-
íèòíîãî èçëó÷åíèÿ íåëèíåéíûé ïî âåêòîð-ïîòåíöèàëó ÷ëåí â (3.2)
ìîæíî îïóñòèòü. Åãî âëèÿíèå ñòàíîâèòñÿ ñóùåñòâåííûì â îñíîâíîì
ïðè èñïîëüçîâàíèè ìîùíîãî èçëó÷åíèÿ ëàçåðîâ. Òàêèì îáðàçîì, â
ïîëóêëàññè÷åñêîì ïðèáëèæåíèè
$
()
$
int
H =−
∑
e
mc
i
i
ii
i
2
Ar P
. (3.3)
Âûðàæåíèå äëÿ äèýëåêòðè÷åñêîé ïðîíèöàåìîñòè òâåðäîãî òåëà
ìîæíî ïîëó÷èòü ìíîãèìè ñïîñîáàìè. Ìû âûáåðåì íå î÷åíü ñòðîãèé,
íî íàãëÿäíûé ïóòü ðåøåíèÿ ýòîé çàäà÷è. Áîëåå ïîñëåäîâàòåëüíî ýòè
ôîðìóëû áóäóò ðàññìîòðåíû â ñëåäóþùèõ ðàçäåëàõ ýòîãî ïàðàãðà-
ôà. Äëÿ íà÷àëà ðàññìîòðèì ïîãëîùåíèå íà ñèñòåìå àòîìîâ, ñëàáî
âçàèìîäåéñòâóþùèõ äðóã ñ äðóãîì.
Êîýôôèöèåíò ïîãëîùåíèÿ
αω()
ìîæío âûðàçèòü ÷åðåç ñå÷åíèå
ïîãëîùåíèÿ íà îäíîì àòîìå
σω αω() ()= N
, ãäå
N
— ÷èñëî àòîìîâ â
ýëåìåíòå îáúåìà. Äëÿ ïðîñòîòû ðàññìîòðèì ïëîñêîïîëÿðèçîâàííóþ
ïàäàþùóþ âîëíó, ðàñïðîñòðàíÿþùóþñÿ â íàïðàâëåíèè îñè
x
(ïðè
ýòîì
~
(knic
x
= + κ)ω
). Âåêòîð-ïîòåíöèàë òàêîé ýëåêòðîìàãíèòíîé
âîëíû ðàâåí
Ar Ae(,) cos( )exp( )ttnxcxc=− −ωω ωκ
ãäå
e
— âåêòîð ïîëÿðèçàöèè ñâåòà, ëåæàùèé â ïëîñêîñòè
yz
. Ïîòîê
ýíåðãèè â ýëåêòðîìàãíèòíîé âîëíå îïèñûâàåòñÿ ñîîòíîøåíèåì
(1.16), à ïîòîê ôîòîíîâ âûðàæàåòñÿ âåëè÷èíîé
SAn
c
x
chhω
ω
π
κω
=−
2
8
2
exp
. (3.4)
Ãàìèëüòîíèàí âçàèìîäåéñòâèÿ âåùåñòâà ñ òàêîé ýëåêòðîìàãíèòíîé
âîëíîé ìîæíî çàïèñàòü â âèäå
$
cos( )
$
int
H =−
−
∑
e
mc
Ae t nxc
xc
ii
i
ωκ
ωω ep
, (3.5)
ãäå ñóììèðîâàíèå ïðîâîäèòñÿ ïî âñåì ýëåêòðîíàì ñ íîìåðàìè
i
. Ïðè
ýòîì ïðåäïîëàãàåòñÿ, ÷òî âçàèìîäåéñòâèå ïðîèñõîäèò òîëüêî ñ ýëåêò-
ðîííîé ïîäñèñòåìîé (
å
— âåëè÷èíà çàðÿäà ýëåêòðîíà,
m
— åãî
§ 3. Ìèêðîñêîïè÷åñêîå îïèñàíèå âçàèìîäåéñòâèÿ ñâåòà ñ âåùåñòâîì 39

ìàññà). Íåïîñðåäñòâåííîå âçàèìîäåéñòâèå ýëåêòðîìàãíèòíîé âîëíû
ñ èîííîé ïîäñèñòåìîé íå ó÷èòûâàåòñÿ. Ýòî âîçìîæíî, åñëè íå ðàññ-
ìàòðèâàòü èíôðàêðàñíóþ îáëàñòü ñïåêòðà, â êîòîðîé ïðîèñõîäèò
ïðÿìîå ïðåâðàùåíèå ôîòîíà â ïîëÿðèçàöèîííûé ôîíîí.
Èñïîëüçîâàíèå òåîðèè âîçìóùåíèé ïðåäïîëàãàåò, ÷òî èçâåñòíû
îñíîâíîå ñîñòîÿíèå è âîçáóæäåííûå ñîñòîÿíèÿ ñèñòåìû, îïèñûâàå-
ìîé ãàìèëüòîíèàíîì
$
H
0
. Êàæäîå èç ýòèõ ñîñòîÿíèé õàðàêòåðèçóåòñÿ
íàáîðîì êâàíòîâûõ ÷èñåë, êîòîðûé ìû áóäåì îáîçíà÷àòü îäíîé áóê-
âîé, íàïðèìåð,
i
äëÿ íà÷àëüíîãî ñîñòîÿíèÿ
i
ñèñòåìû èëè
f
äëÿ êî-
íå÷íîãî ñîñòîÿíèÿ
f
. Íèæå ÷àùå âñåãî áóäóò èñïîëüçîâàòüñÿ äèðà-
êîâñêèå îáîçíà÷åíèÿ âåêòîðîâ ñîñòîÿíèé (ñ èñïîëüçîâàíèåì óãëîâûõ
ñêîáîê), íî â íåêîòîðûõ ñëó÷àÿõ áóäóò âûïèñûâàòüñÿ ïîëíûå øðå-
äèíãåðîâñêèå âîëíîâûå ôóíêöèè, â òîì ÷èñëå èõ ÿâíàÿ çàâèñèìîñòü
îò êîîðäèíàò ãèëüáåðòîâà ïðîñòðàíñòâà.
Ñðåäè êâàíòîâûõ ÷èñåë, êîòîðûå õàðàêòåðèçóþò ñîñòîÿíèÿ ñèñ-
òåìû ñ íåâîçìóùåííûì ãàìèëüòîíèàíîì
$
H
0
, ÷àñòî óäîáíî âûäåëèòü
ýíåðãèþ ñîñòîÿíèÿ
E
α
(äëÿ ñîñòîÿíèÿ
α
) è ïîëíûé èìïóëüñ
P
α
.Â
ñëó÷àå ñòàöèîíàðíîé îäíîðîäíîé ñèñòåìû ýíåðãèÿ è èìïóëüñ, ñîîò-
âåòñòóþùèå ñîáñòâåííûì ñîñòîÿíèÿì ãàìèëüòîíèàíà, ñîõðàíÿþòñÿ è
ÿâëÿþòñÿ õîðîøèìè êâàíòîâûìè ÷èñëàìè. Âîîáùå ãîâîðÿ, ïðîáëåìà
íàõîæäåíèÿ ñîáñòâåííûõ ñîñòîÿíèé è ñîîòâåòñòâóþùèõ ñîáñòâåííûõ
çíà÷åíèé ýíåðãèè è ïîëíîãî èìïóëüñà íå èìååò òî÷íîãî ðåøåíèÿ. Ðàç-
ðàáîòàíî áîëüøîå ÷èñëî ïðèáëèæåííûõ ìåòîäîâ èõ íàõîæäåíèÿ.
Çäåñü ìû áóäåì ïðåäïîëàãàòü, ÷òî ýòà ïðîáëåìà óæå ðåøåíà, è èçâåñ-
òåí ïîëíûé íàáîð ñîñòîÿíèé
α
ñèñòåìû, ñîòâåòñòâóþùèå ãàìèëüòî-
íèàíó
$
H
0
, íå âîçìóùåííîìó âíåøíèì ýëåêòðîìàãíèòíûì ïîëåì.
 ïîëóêëàññè÷åñêîì ïðèáëèæåíèè ïðåäïîëàãàåòñÿ, ÷òî òâåðäîå
òåëî íàõîäèòñÿ â îäíîì èç ñîñòîÿíèé
i
, è ïåðåõîä ïðîèñõîäèò â äðó-
ãîå ñîñòîÿíèå
f
ïîä äåéñòâèåì âíåøíåãî ýëåêòðîìàãíèòíîãî ïîëÿ.
Âåðîÿòíîñòü ïåðåõîäà èç ñîñòîÿíèÿ
i
â ñîñòîÿíèå
f
ïîä äåéñòâèåì
âîçìóùåíèÿ (3.5) ìîæíî âû÷èñëèòü, èñïîëüçóÿ «Çîëîòîå ïðàâèëî
Ôåðìè»:
wfiEE
e
mc
Af e
if f
i
inx c
=−+=
=
−
2
2
1
2
2
222
2
πδω
π
ω
hh
h
$
()
int
H
−
∑
−
ωκ
δω ω
xc
j
j
fi
i
$
(),pe
2
ãäå
ω
fi f
i
EE=−()h
— ÷àñòîòà ïåðåõîäà èç îäíîãî ýëåêòðîííîãî ñîñ-
òîÿíèÿ â äðóãîå. ×òîáû ïîëó÷èòü ïàðöèàëüíîå ñå÷åíèå ïîãëîùåíèÿ
íà îäíîì àòîìå, íåîáõîäèìî
w
fi
ïîäåëèòü íà ïîòîê ôîòîíîâ (3.4):
40 Ãëàâà 1. Âçàèìîäåéñòâèå ýëåêòðîìàãíèòíîãî ïîëÿ ñ òâåðäûì òåëîì
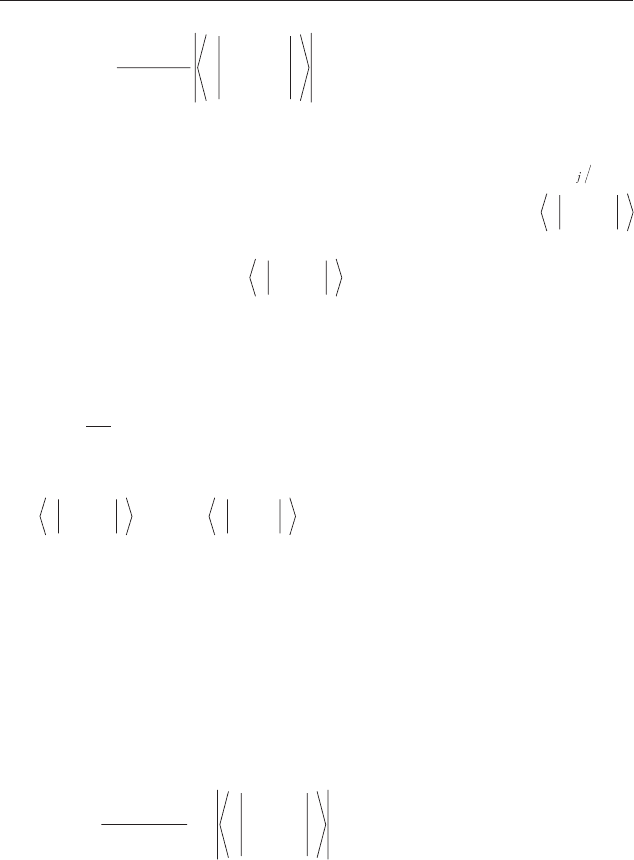
σω
π
ω
δω ω
if
j
j
fi
e
mcn
fi()
$
(),=−
∑
4
22
2
2
h
pe
(3.6)
Çäåñü ïðåäïîëàãàåòñÿ, ÷òî ðàáîòàåò äèïîëüíîå ïðèáëèæåíèå — äëè-
íà âîëíû èçëó÷åíèÿ ìíîãî áîëüøå õàðàêòåðíûõ ðàçìåðîâ âîëíîâûõ
ôóíêöèé ýëåêòðîíîâ. Ïîýòîìó â ðàçëîæåíèè ýêñïîíåíòû
e
inx cω
îñ-
òàâëåí òîëüêî íóëåâîé ÷ëåí. Ïðè ýòîì ìàòðè÷íûé ýëåìåíò
fi
j
$
p
∑
ñ÷èòàåòñÿ îòëè÷íûì îò íóëÿ. Åñëè æå ñèììåòðèÿ íà÷àëüíîãî è êîíå÷-
íîãî ñîñòîÿíèé òàêîâà, ÷òî
fi
j
$
p
∑
=0
, íåîáõîäèìî ó÷èòûâàòü ñëå-
äóþùèå ÷ëåíû ðàçëîæåíèÿ ýêñïîíåíòû â ðÿä. Ýòî ïðèâîäèò ê ïðî-
öåññàì ìàãíèòíî-äèïîëüíîãî è êâàäðóïîëüíîãî ïîãëîùåíèÿ ñâåòà.
Äëÿ ïðåîáðàçîâàíèÿ âûðàæåíèÿ (3.6) ìîæíî âîñïîëüçîâàòüñÿ
èçâåñòíûì êîììóòàöèîííûì ñîîòíîøåíèåì
$
$
,.pr
jj
im
=
h
[]H
÷òî ïðèâîäèò ê ðàâåíñòâó
fiimfi
j
fi
j
$
pr
∑∑
=ω
.
Äëÿ òîãî ÷òîáû ïåðåéòè îò ñå÷åíèÿ ïîãëîùåíèÿ äâóõóðîâíåâîé
ñèñòåìû ê êîýôôèöèåíòó ïîãëîùåíèÿ ýëåêòðîìàãíèòíîãî èçëó÷åíèÿ
â òâåðäîì òåëå, íåîáõîäèìî ó÷åñòü äâà îáñòîÿòåëüñòâà. Âî-ïåðâûõ,
íåîáõîäèìî ïðîñóììèðîâàòü (3.6) ïî âñåì âîçìîæíûì êîíå÷íûì ñîñ-
òîÿíèÿì â òâåðäîì òåëå, èñêëþ÷àÿ çàíÿòûå ñîñòîÿíèÿ (â ñîîòâåòñòâèè
ñ ïðèíöèïîì Ïàóëè). Âî-âòîðûõ, ïðè íåíóëåâîé òåìïåðàòóðå òâåð-
äîå òåëî íå íàõîäèòñÿ â ñâîåì îñíîâíîì ñîñòîÿíèè. Ïðè êîíå÷íîé
òåìïåðàòóðå ìîæíî ââåñòè ôóíêöèþ ðàñïðåäåëåíèÿ ïî ýíåðãèè
fE()
,
îïèñûâàþùóþ çàñåëåííîñòü êâàíòîâûõ ñîñòîÿíèé. Ïðè ýòîì êîýô-
ôèöèåíò ïîãëîùåíèÿ ïðèîáðåòàåò âèä
αω
πω
δω ω
()
[ ( )] ( ) (
,
=×
×− −
∑∑
4
1
22
2
eN
cn
fi
fE fE
j
jif
f
i
fi
h
re
),
(3.7)
à ìíèìàÿ ÷àñòü äèýëåêòðè÷åñêîé ïðîíèöàåìîñòè ðàâíà
§ 3. Ìèêðîñêîïè÷åñêîå îïèñàíèå âçàèìîäåéñòâèÿ ñâåòà ñ âåùåñòâîì 41
