Ваняшов А.Д., Кустиков Г.Г. Учебное пособие для курсового проектирования - Расчет и конструирование центробежных компрессорных машин
Подождите немного. Документ загружается.

140
d
2
b
3
d1
I
I
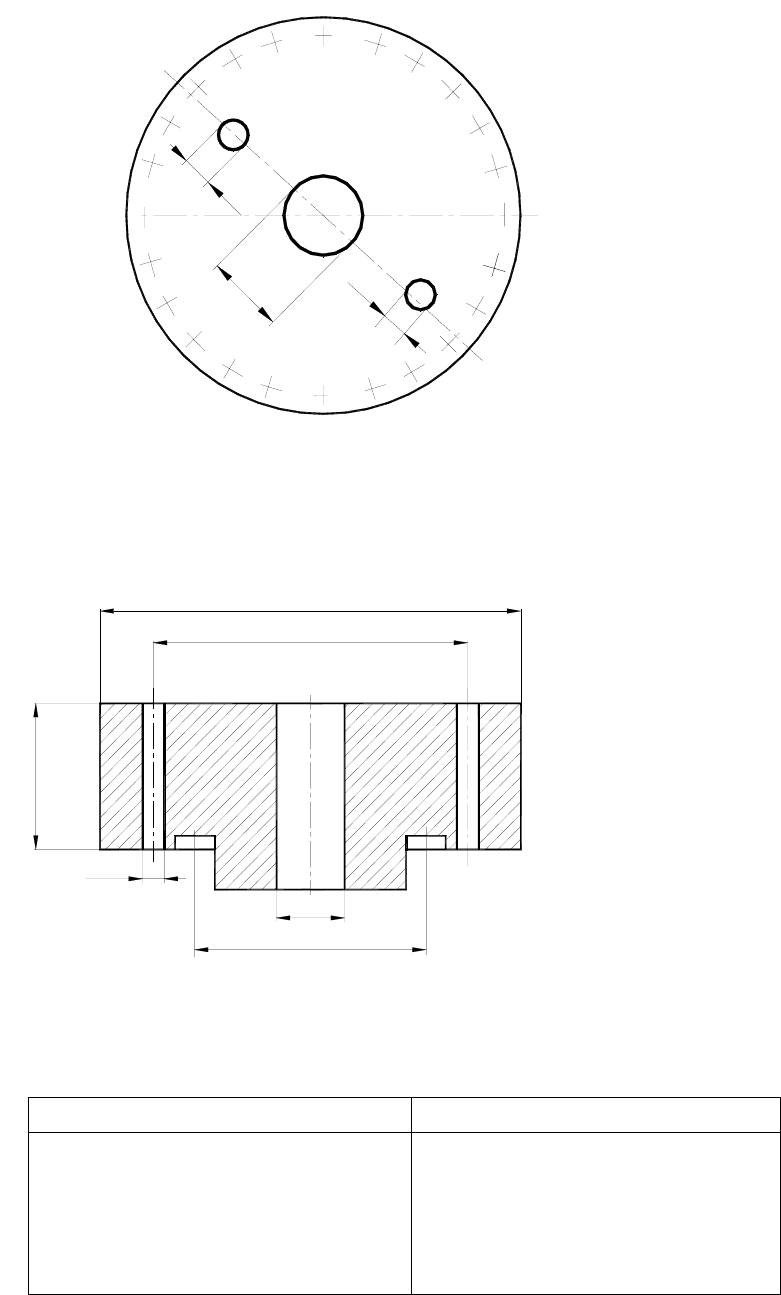
Рис. 2.18. Схема для определения максимальной суммы длин хорд
отверстий в наиболее ослабленном диаметральном сечении I-I:
d
1
, d
2
, – диаметры отверстий; b
3
– хорда отверстия;
321
bddd
i
++=
∑
Da
Dб
SП
Dср
dо.ш
d2
Рис. 2.19. Расчетная схема к определению размеров плоской крышки
Таблица 2.4
Материал прокладки
σ
см
, МПа
Алюминий
Медь
Сталь углеродистая
Сталь легированная
Сталь высоколегированная
68,67
98,1
122,62
122,62
176,58
Исполнительная ширина прокладки выбирается в зависимости от
расчетной ширины по условию
р
bb ≥
.

141
Расчетная ширина прокладки
⎪
⎪
⎭
⎪
⎪
⎬
⎫
⎪
⎪
⎩
⎪
⎪
⎨
⎧
⋅−⋅
⋅⋅
⋅−−⋅
⋅
=
)1,1][4(
1,1
)25,0]([4
max
20
1
1
ик
и
рсмк
р
р
Р
DР
Р
DP
b
σ
σσ
,
где [
σ
к
], [
σ
к
]
20
– допускаемые контактные напряжения на уплотнительных
поверхностях затвора соответственно при расчетной температуре и
температуре 20 °С.
Допускаемые контактные напряжения на уплотнительных поверхностях
затвора принимаются в зависимости от наименьшего значения предела
текучести материалов корпуса и крышки:
−
если
68,274
min
≤
Т
σ
МПа, то
min
][
Тк
σσ
=
;
−
если
68,274
min
>
Т
σ
МПа, то
18035,0][
min
+⋅=
Тк
σσ
МПа.
3. Расчет критических частот вращения ротора
Расчет частот собственных колебаний ротора центробежного
компрессора производится с целью проверки его виброустойчивости, т.е.
сопоставления рабочей частоты вращения, известной из газодинамического
расчета, с первой и второй критическими частотами.
Рабочая угловая скорость вращения ротора, рад/с:
30
об
n
π
ω
=
,
где n
об
– в об/мин.
Условия виброустойчивости:
−
для жестких роторов
)8,07,0(
−
≤
крI
ω
ω
;
−
для гибких роторов
)8,07,0()3,12,1( −
≤
≤
−
крIIкрI
ω
ω
ω
.
Значение первой критической частоты вращения можно с достаточной
для инженерных расчетов точностью рассчитать по одной из известных
методик. Некоторые из них приведены ниже, а значение второй критической
частоты приближенно можно найти из соотношения
крIкрII
ω
ω
⋅
−
=
)9,36,3(
.
3.1. Метод Донкерли
Первая критическая частота по этому методу находится из условия
22
3
2
2
2
1
2
1
...
1111
крiкркркркр
ωωωωω
++++=
, (3.1)
142
где
)(1
)1(1111
δω
m
кр
=
;
)(1
)2(1122
δω
m
кр
=
;...;
)(1
)(11 iiкрi
m
δω
=
- критические
угловые скорости ротора при условии размещения на нем только одной
массы, рад/с; m
i
– массы дисков, размещенных на роторе;
δ
11(i)
– коэффициент
влияния (прогиб вала от силы, равной 1Н, приложенной в точке крепления
массы на валу) при установке на валу одного i-го диска, м/Н.
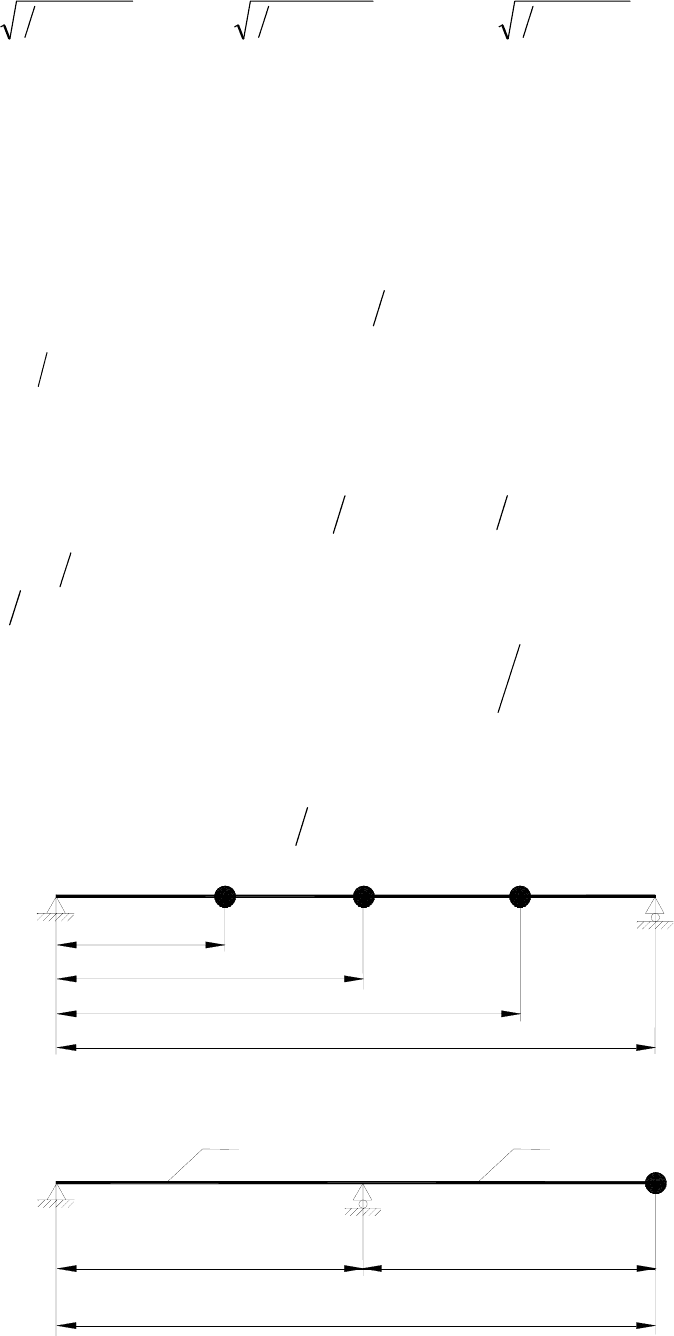
Коэффициенты влияния определены для типовых схем однопролетных
и консольных роторов (рис. 3.1).
Для однопролетных роторов (рис. 3.1 а)
)3()(
2
2
)(11
LEIlLl
iiii
−=
δ
, (3.2)
где
6
4
4
ii
dI ⋅=
π
- момент инерции сечения вала диаметром d
i
в месте
приложения сосредоточенной нагрузки массой m
i
, м
4
; Е – модуль упругости
(модуль Юнга), Па.
Для консольных роторов (рис. 3.1 б)
)3()3(
11
3
11
2
11)11(11 −−−−
+= EILEILL
ср
δ
, (3.3)
где
64
4
срср
dI
π
=
- осредненный момент инерции пролета вала;
64
4
1111 −−
= dI
π
- момент инерции консоли вала.
Средний диаметр вала пролета
ndd
n
i
iср
⎟
⎠
⎞
⎜
⎝
⎛
=
∑
=1
, где n – количество
закрепленных на валу масс.
Для консольного вала постоянного поперечного сечения формула (3.3)
упрощается:
)3(
2
11211
EILL
−
=
δ
.
d1
L
L2
L1
d2
m1
l1
l2
mim2
li
а)
L
m
б)
Рис. 3.1. Схемы к расчету критической частоты по методу Донкерли:
а) однопролетный ротор; б) консольный ротор

143
3.2. Метод Рэллея
Частота собственных колебаний определяется по методу Рэллея из
условия равенства максимальных значений потенциальной П
max
и
кинетической К
max
энергий ротора во время изгибных колебаний. При
отсутствии трения
maxmax
KП
=
,
где
∑
⋅= )(
2
1
max ii
yFП
;
∑
⋅= )(
2
2
2
max ii
yF
g
К
ω
.
В выражениях потенциальной и кинетической энергий в качестве кривой
прогиба ротора при его изгибных колебаниях принимается упругая линия
вала при статической нагрузке от закрепленных на валу деталей.
Первая критическая частота по методу Рэллея, рад/с:
∑
∑
⋅
⋅⋅
=
)(
)(
2
ii
ii
кр
yF
yFg
ω
, (3.4)
где
gmF
ii
⋅=
- сосредоточенная сила, действующая на вал и приложенная в
центре тяжести соответствующего участка, Н; y
i
– величина статического
прогиба ротора, м.
Реальный ротор представляет собой систему с сосредоточенными
(детали, насаженные на вал) и распределенными (участки вала переменного
диаметра) нагрузками. Для упрощения расчетов распределенную массу вала
заменяют некоторым количеством сосредоточенных масс. Для этого вал
разбивается на участки, и каждый участок вала с распределенной массой
заменяется невесомым валом
с одной сосредоточенной массой,
расположенной в центре тяжести участка. На тех участках вала, на которых
имеются сосредоточенные массы (диски, муфты и др.), они суммируются с
массой этих участков.
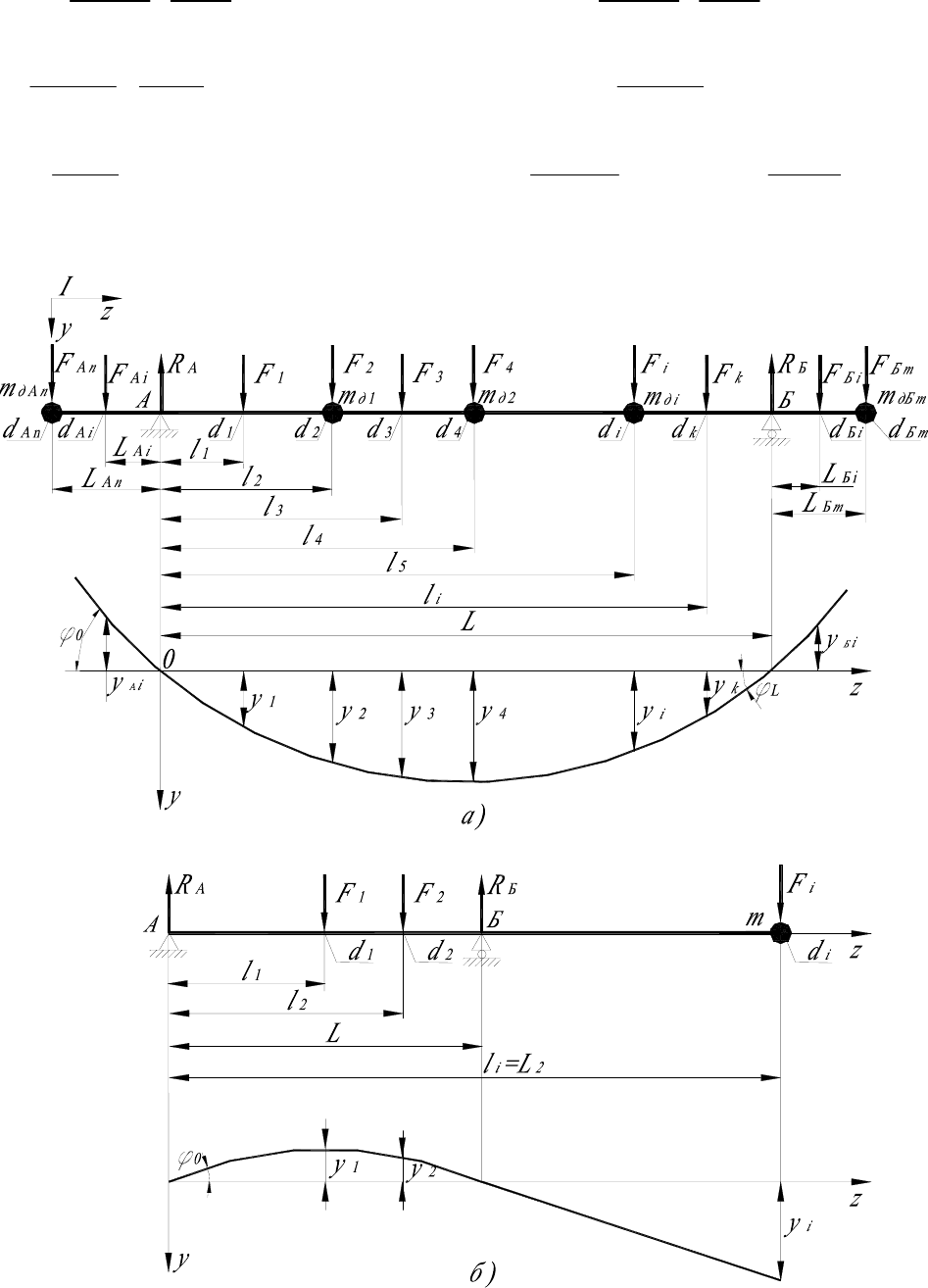
Если ротор имеет консольные участки левее и правее опор, то
целесообразно воспользоваться двумя или даже тремя местными системами
координат (рис. 3.2).
Массы сосредоточенных
нагрузок определяются по выполненным
чертежам деталей. Приведенные массы участков вала рассчитываются как
i
уч
i
мi
l
d
m
4
2
⋅
=
π
ρ
,
где ρ
м
– плотность материала вала, кг/м
3
; d
i
– диаметр участка вала, м; l
уч
i
-
длина участка приложения распределенной нагрузки (участка постоянного
диаметра).
Функция статического прогиба для пролета однопролетного ротора (рис.
3.2) описывается формулой (начало координат в точке приложения крайней
силы на участке левее опоры А, ось z направлена вправо) [25]

144
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−+−+
++−−+−+
+−−−−+⋅
++=
∑
∑
∑
=
=
=
=
−=
=
mi
i
БiAnБi
AnБ
ki
i
iAni
AnA
ni
i
AiAnAiAn
i
LLLzF
LLzRlLzF
LzRLLzFzF
EI
zyzy
1
3
3
1
3
3
1
1
33
max
00
))((
))(())((
)())((
6
1
)(
ϕ
, (3.5)
где z – текущая координата, направленная вдоль оси ротора; R
A
, R
Б
– реакции
опор А и Б, Н (рис. 3.2); l
i
– расстояние от опоры А до линии действия силы
F
i
, м; L
Ai
– расстояние от опоры А до линии действия силы F
Ai
, м; L
Бi
–
расстояние от опоры Б до линии действия силы F
Бi
, м; n, m, k – количество
сил соответственно левее опоры А, правее опоры Б, между опорами; Е -
модуль Юнга, Па;
64
4
maxmax
dI ⋅=
π
– максимальный момент инерции
поперечного сечения ротора, м
4
; d
max
– максимальный диаметр вала, м; L –
длина ротора между опорами, м; y
0
и φ
0
– линейный и угловой прогибы
ротора, находящиеся из граничных условий.
Граничные условия задаются из условия равенства нулю прогибов в
опорах ротора. Например, для схемы рис. 3.2 а:
.0))((
,0)(
=+=
=
=
An
An
LLzy
Lzy
При подстановке этих граничных условий в уравнение прогибов (3.5)
получим выражения для нахождения у
0
и φ
0
.
Подставляя первое граничное условие в выражение (3.5), получим
∑
=
=
++=
ni
i
AiАiAn
LF
EI
Ly
1
3
max
00
)(
6
1
0
ϕ
,
∑
=
=
−−=
ni
i
AiАiAn
LF
EI
Ly
1
3
max
00
)(
6
1
ϕ
. (3.6)
Подставляя второе граничное условие в выражение (3.5), получим
⎟
⎠
⎞
⎜
⎝
⎛
−+−++++=
∑∑
=
=
=
=
ki
i
iiA
ni
i
AiAiАn
lLFLRLLF
EI
LLy
1
33
1
3
max
00
)()(
6
1
)(0
ϕ
,
)(
)()(
6
1
1
33
1
3
max
0
0
LL
lLFLRLLF
EI
y
Аn
ki
i
iiA
ni
i
AiAi
+
⎟
⎠
⎞
⎜
⎝
⎛
−+−+−−
=
∑∑
=
=
=
=
ϕ
.
Подставляя последнее выражение в формулу (3.6):
∑
∑∑
=
=
=
=
=
=
−
+
⎟
⎠
⎞
⎜
⎝
⎛
−+−++
=
ni
i
AiАiAn
Аn
ki
i
iiA
ni
i
AiAi
LF
EI
L
LL
lLFLRLLF
EI
y
y
1
3
max
1
33
1
3
max
0
0
)(
6
1
)(
)()(
6
1
,
145
∑∑∑
=
=
=
=
=
=
−
+
⎟
⎠
⎞
⎜
⎝
⎛
−+−++
+
=
ni
i
AiАi
Аn
An
ki
i
iiA
ni
i
AiAi
Аn
An
LF
EILL
L
lLFLRLLF
EILL
L
yy
1
3
max
1
33
1
3
max
00
)(
6
1
)(
)()(
6
1
)(
,
⎭
⎬
⎫
⎩
⎨
⎧
−
+
⎟
⎠
⎞
⎜
⎝
⎛
−+−+=
+
∑∑∑
=
=
=
=
=
=
ni
i
AiАi
Аn
An
ki
i
iiA
ni
i
AiAi
Аn
LF
LL
L
lLFLRLLF
EILL
L
y
1
3
1
33
1
3
max
0
)(
)(
)()(
6
1
)(
,
L
LL
LF
LL
L
lLFLRLLF
EI
y
An
ni
i
AiАi
Аn
An
ki
i
iiA
ni
i
AiAi
+
⎭
⎬
⎫
⎩
⎨
⎧
−
+
⎟
⎠
⎞
⎜
⎝
⎛
−+−+=
∑∑∑
=
=
=
=
=
= 1
3
1
33
1
3
max
0
)(
)(
)()(
6
1
. (3.7)
Рис. 3.2. Расчетные схемы к определению критической частоты по методу
Рэллея: а) однопролетный ротор; б) консольный ротор
146
Подставляя полученное выражение в формулу (3.5), найдем
ϕ
0
:
An
ni
i
AiАi
L
LF
EI
y
∑
=
=
−−
=
1
3
max
0
0
)(
6
1
ϕ
. (3.8)
Реакция опоры находится из условия равенства нулю моментов сил
относительно противоположной опоры, например:
∑
= 0
Б
М
;
0)()(
111
=++−−−
∑∑∑
=
=
=
=
=
=
mi
i
БiБi
ni
i
АiАi
ki
i
iiA
LLFLFlLFLR
,
где F
Ai
, F
Бi
– сосредоточенные силы, приложенные на консолях
соответственно левее опоры А и правее опоры Б, Н; L
Ai
, L
Бi
– расстояния до
точки приложения сил F
Ai
, F
Бi
от соответствующей опоры.
Реакция опоры Б R
Б
находится аналогично из условия
∑
= 0
А
М
.
Для расчетной схемы консольного ротора (рис. 3.2 б) граничные условия
записываются следующим образом:
,0)(
,0)0(
0
==
===
Lzy
yzy
а функция статических прогибов имеет вид
⎟
⎠
⎞
⎜
⎝
⎛
−+−−−+++=
∑∑
=
=
=
=
mi
i
iiБ
ki
i
iiAi
LzFLzRlzFzR
EI
zyzy
1
33
1
33
max
00
)()()(
6
1
)(
ϕ
.
3.3. Метод приведения
Расчетные схемы к определению
ω
кр
для консольных и однопролетных
роторов показаны на рис. 3.3. Сущность метода заключается в том, что
приложенные к валу нагрузки приводятся к точке приведения, которая для
однопролетных роторов соответствует середине пролета между опорами АБ,
для консольных – точке В закрепления массы на консоли.
Используемые в этом методе формулы для удобства вычислений
представлены в
безразмерном виде.
3.3.1. Расчет однопролетных роторов
Расчетная схема однопролетного ротора показана на рис. 3.3 а.
Собственная частота колебаний, рад/с:
м
Акр
кр
Е
L
d
ρ
ω
ω
⋅
⋅
⋅
=
2
4
, (3.9)
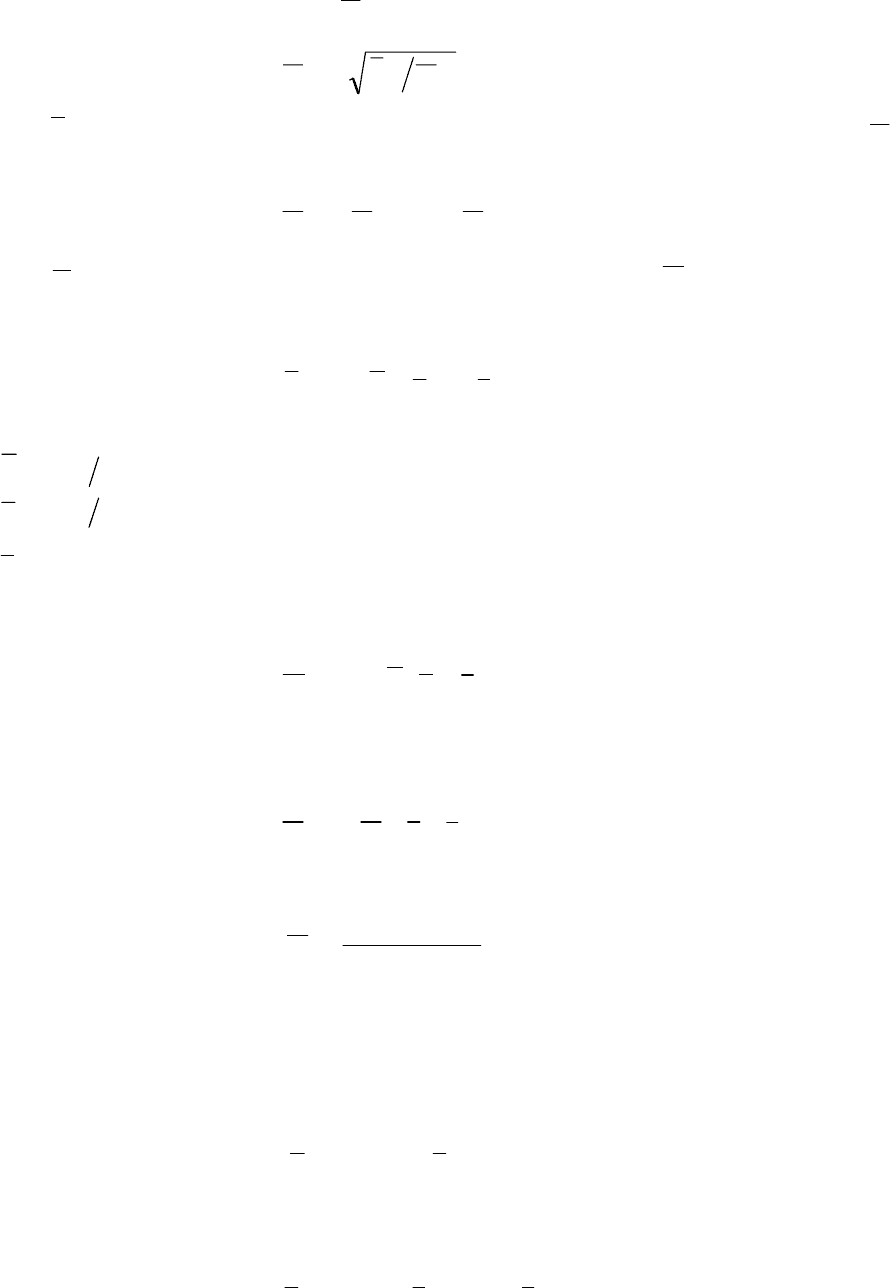
147
где Е,
ρ
м
– модуль упругости и плотность материала вала, Па, кг/м
3
; d
А
–
диаметр вала на опоре А, м;
кр
ω
- относительная критическая скорость вала.
прпркр
mk=
ω
, (3.10)
где
пр
k
- относительный приведенный коэффициент жесткости вала;
пр
m
-
относительная приведенная масса ротора.
∑
+=
npiпрвпр
mmm
..
, (3.11)
где
прв
m
.
- относительная приведенная масса вала;
прi
m
.
- относительная
приведенная масса i-го элемента, закрепленного на валу.
zdydk
zzпр
2
1
0
4
)(
∫
′′
=
, (3.12)
Аzz
ddd =
- относительный диаметр вала в сечении с координатой ⎯z;
max
yyy
zz
=
- относительный прогиб вала в сечении с координатой ⎯z;
Lzz /=
- относительная координата однопролетного вала.
Относительная приведенная масса вала для однопролетных роторов
zdydm
zzпрв
∫
=
1
0
22
.
. (3.13)
Относительная приведенная масса i-го элемента, закрепленного на валу:
zdymm
ziпрi
∫
=
1
0
.
. (3.14)
Относительная масса i-го элемента, закрепленного на валу:
Ld
m
m
А
i
i
⋅⋅⋅
⋅
=
ρπ
2
4
, (3.15)
где
i
m
- масса i-го элемента, кг.
Относительный прогиб вала в сечении с координатой z для
однопролетных роторов может быть задан двумя функциями.
Функция относительных прогибов в виде синусоиды [15]
)sin( zy
z
⋅
=
π
.
Функцию статических прогибов можно аппроксимировать полиномом
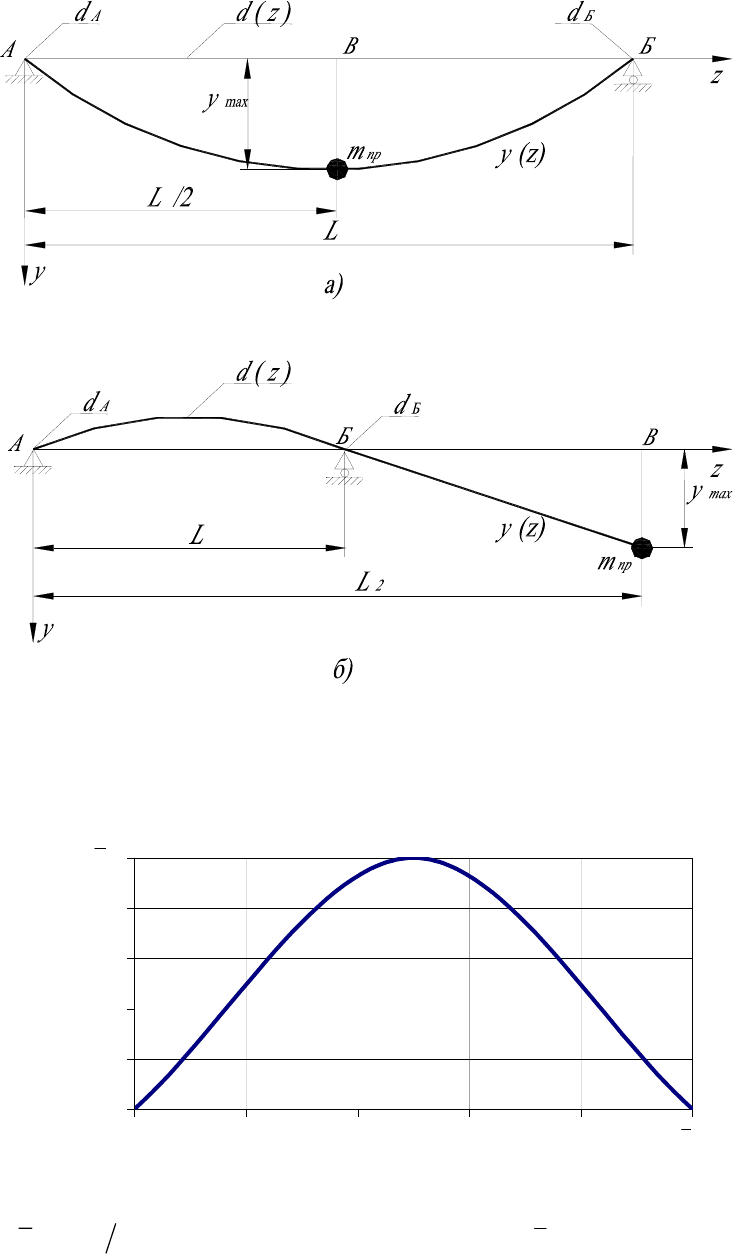
2-й степени (рис. 3.4):
zzy
z
⋅+⋅−= 0,40,4
2
.
Метод приведения позволяет вводить в расчетные формулы (3.12) и
(3.13) функциональную зависимость диаметра вала от его длины, например, в
148
виде полинома 3-й степени. Примерный вид этих зависимостей для роторов
центробежных нагнетателей природного газа показан на рис. 3.5 и 3.6. Эти
зависимости аппроксимируются полиномами с различными
коэффициентами.
Рис. 3.3. Расчетная схема к определению критической частоты по
методу приведения: а) однопролетный ротор; б) консольный ротор
0
0,2
0,4
0,6
0,8
1
0 0,2 0,4 0,6 0,8 1
z
y
z
Рис. 3.4. Зависимость относительных прогибов однопролетного ротора
max
yyy
zz
=
от относительной его длины
Lzz /
=
149
1
1,1
1,2
1,3
1,4
1,5
0 0,2 0,4 0,6 0,8 1
z
d
z
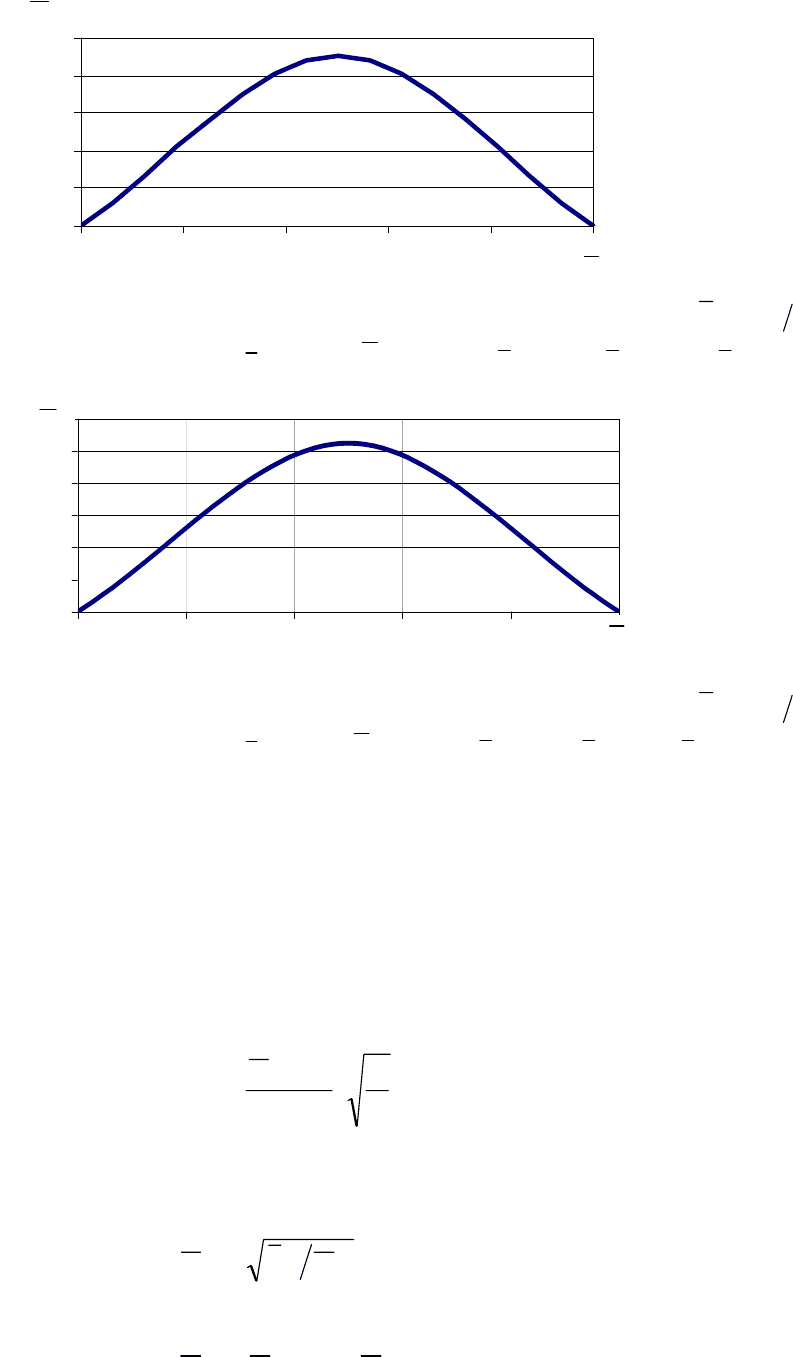
Рис. 3.5. Графическая зависимость относительного диаметра вала
Аzz
ddd =
от относительной его длины
Lzz /
=
:
18,02,10,2
23
+⋅+⋅+⋅−= zzzd
z
1
1,2
1,4
1,6
1,8
2
2,2
00,20,40,60,81
z
d
z
Рис. 3.6. Графическая зависимость относительного диаметра вала
Аzz
ddd =
от относительной его длины
Lzz /
=
18,10,38,4
23
+⋅+⋅+⋅−= zzzd
z
3.3.2. Расчет консольных роторов
Расчетная схема однопролетного ротора показана на рис. 3.3 б.
Собственная частота колебаний, рад/с:
ρ
ω
ω
Е
L
d
Бкр
кр
⋅
⋅
⋅
=
2
2
4
,
где d
Б
– диаметр вала на опоре Б, м.
Относительная критическая скорость вала по формуле (3.10)
прпркр
mk=
ω
.
Относительная приведенная масса ротора по формуле (3.11)
∑
+=
npiпрвпр
mmm
..
.
Относительный приведенный коэффициент жесткости по формуле (3.12)
