Ваняшов А.Д., Кустиков Г.Г. Учебное пособие для курсового проектирования - Расчет и конструирование центробежных компрессорных машин
Подождите немного. Документ загружается.

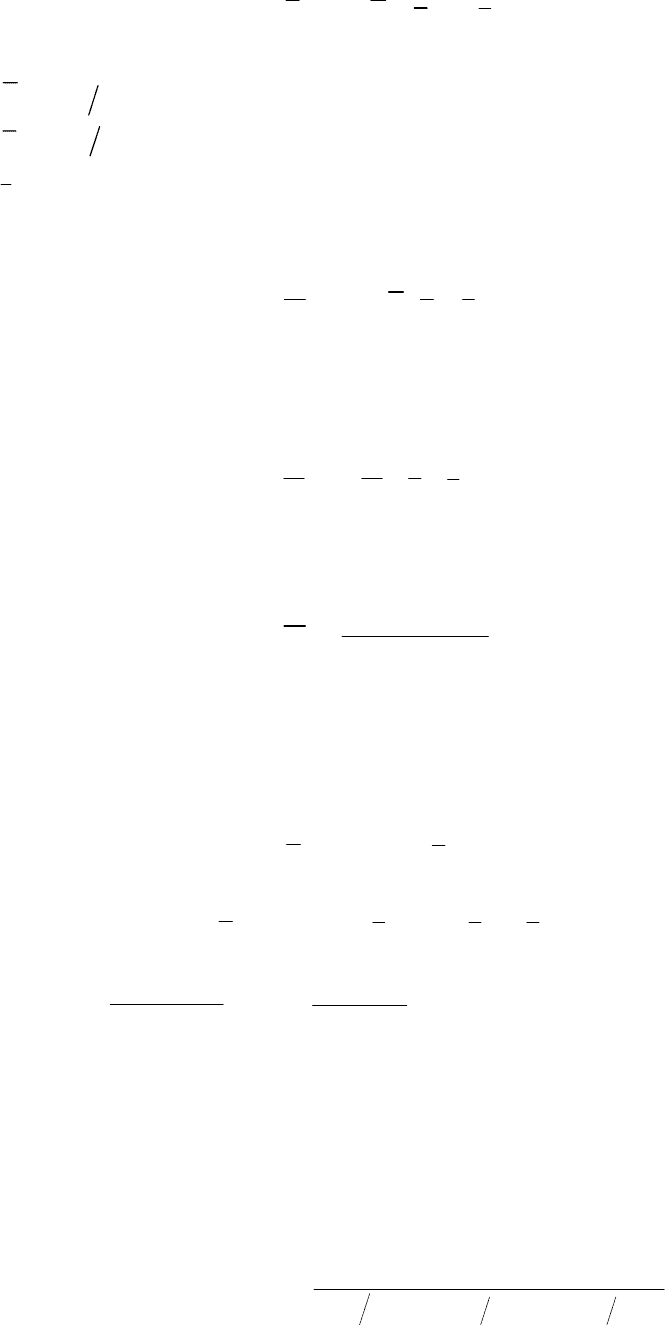
150
zdydk
zzпр
2
1
0
4
)(
∫
′′
=
.
Бzz
ddd =
- относительный диаметр вала в сечении с координатой ⎯z;
max
yyy
zz
=
- относительный прогиб вала в сечении с координатой ⎯z;
Lzz /=
- относительная координата консольного вала.
Относительная приведенная масса вала по формуле (3.13):
zdydm
zzпрв
∫
=
1
0
22
.
.
Относительная приведенная масса i-го элемента, закрепленного на валу
по формуле (3.14):
zdymm
ziпрi
∫
=
1
0
.
.
Относительная масса i-го элемента, закрепленного на валу, по формуле
(3.15):
2
2
4
Ld
m
m
Б
i
i
⋅⋅⋅
⋅
=
ρπ
;
где
i
m
- масса i-го элемента, закрепленного на валу, кг.
Относительный прогиб вала в сечении с координатой z для консольных
роторов:
для пролета АБ (рис. 3.3 б)
)sin( zy
z
⋅
=
π
;
для консоли БВ (рис. 3.3 б)
)6/5,0(
32
23
zzzbby
z
+⋅+⋅⋅=
,
где
экв
А
IL
IL
b
⋅⋅
⋅
=
1
2
3
;
3/1
1
2
3
+
=
b
b
;
экв
I
- эквивалентный момент инерции
сечения вала в пролете АБ.
Для консольного вала постоянного поперечного сечения
IIII
БАэкв
===
.
Эквивалентный момент инерции пролета АБ с двумя ступенями
диаметрами d
A1
и d
A2
(рис. 3.7)
)1()()(
1
21
3
121
1
AAAАА
Аэкв
IILlII
II
−+
=
,
с тремя ступенями диаметрами d
A1
, d
A2
, d
A3
(рис. 3.7)
151
)()()1()()(
1
3121
3
221
3
131
1
AAAAAAAAАА
Аэкв
IIIILlIILlII
II
−+−+
=
.
Для схемы консольного ротора с расположением опор по относительной
координате
Lzz /
=
, равной соответственно 0 и 0,75, аппроксимацией
функции статических прогибов ротора совместно для двух участков (между
опорами и консоли) получена формула в виде квадратичного полинома (рис.
3.8)
zzy
z
⋅+⋅−= 3,23,3
2
.
В связи с тем что в расчетных формулах (3.8)-(3.10) значения прогибов
должны принимать только положительные значения, полная длина ротора
разбивается на два участка: участок АБ – между опорами (рис. 3.3 б) и
участок БВ - консоль. Поэтому графическая зависимость (рис. 3.9) и
расчетные формулы прогибов выглядят следующим образом:
75,00 ≤≤ z
:
zzy
z
⋅+⋅−= 3,23,3
2
,
175,0 ≤≤ z
:
zzy
z
⋅−⋅= 3,23,3
2
.
Интегралы в формулах (3.8)-(3.10) для консольных роторов берутся
поочередно для двух участков с последующим суммированием полученных
результатов.
Если диаметр сечений вала изменяется по длине незначительно (в
пределах 10 %), в расчетных формулах можно использовать схему с
постоянным диаметром вала. В этом случае относительный диаметр вала
1=
z
d
.
L2
L
A Б
l
A1
lA2
lA3
dA1
dA2
dA3
В
dБ
mпр
Рис. 3.7. Расчетная схема консольного ступенчатого вала
152
-1
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0 0,2 0,4 0,6 0,8 1
z
y
z
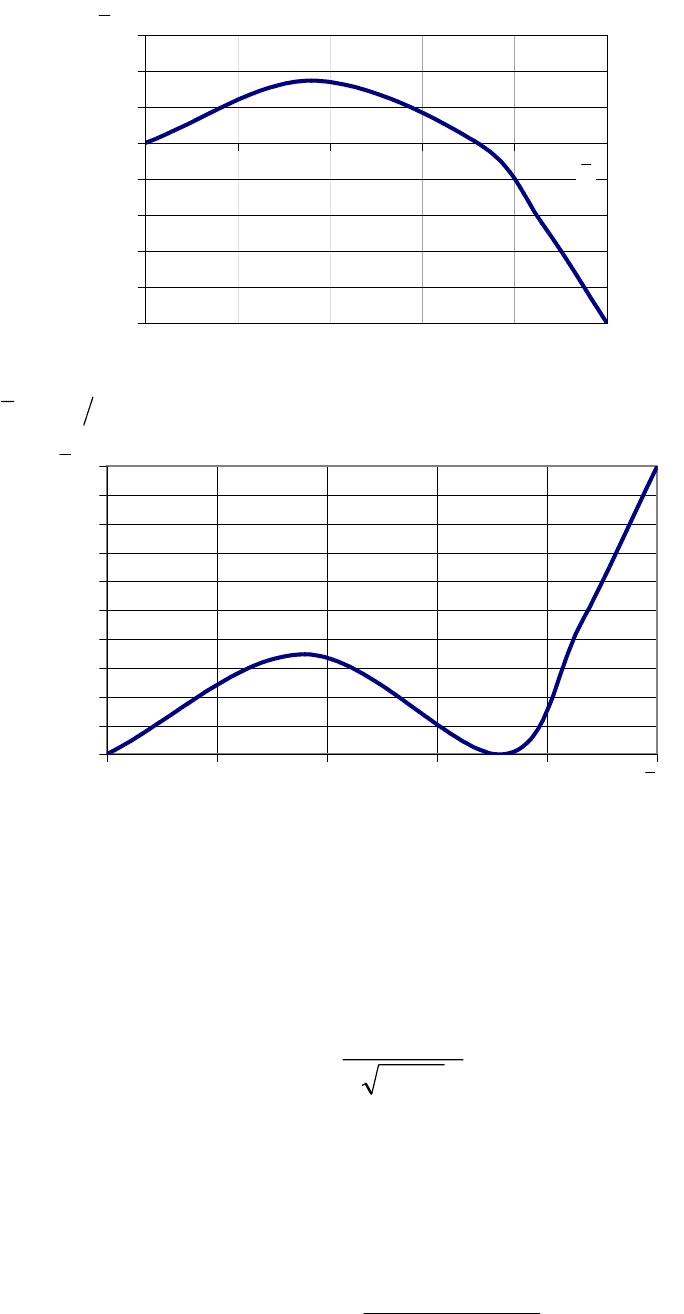
Рис. 3.8. Зависимость относительных прогибов консольного ротора
max
yyy
zz
=
от относительной его длины
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
00,20,40,60,81
z
y
z
Рис. 3.9. Функция прогибов консольного ротора в положительной области
3.4. Приближенные оценочные формулы
Формула Звягинцева В.В. [27] для n
кр
, в об/мин :
LM
Ld
n
кр
/
)/(
10503,7
2
max
6
⋅=
,
где d
max
– максимальный диаметр вала, м; М – масса ротора, кг.
∑
+=
iв
mmМ
.
Формула Риса В.Ф. [2] для n
кр
, в об/мин :
2
)3,2(
1000
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⋅=
срd
кр
DXK
d
n
,
где К
d
= 0,019-0,027; D
ср
– средний диаметр рабочих колес на валу, м;
X – количество ступеней; d – средний диаметр вала, м.
153
4. Примеры конструктивных и прочностных расчетов
4.1. Пример расчета осевого усилия и размеров устройств,
его компенсирующих
Пример расчета осевых усилий выполним для центробежного
нагнетателя природного газа производительностью по условиям всасывания
н
Q
= 340 м
3
/мин (Р
н
= 4,967 МПа; Т
н
= 288 К) и отношением давлений
π
к
= 1,5.
Исходные данные для расчета осевых усилий возьмем из
термогазодинамического расчета проточной части нагнетателя.
Необходимые данные приведем в табл. 4.1.
Таблица 4.1
Исходные данные
№ ступени
№ п/п Параметр Размерность
1 2
1
G
кг/c 213
2
n
об
об/мин 5300
3
ω
рад/с 555,0
4
Р
н
МПа 4,967
5
ψ
Т2
-
0,645 0,645
6 U
2
м/с 228,2 228,2
7 D
2
м 0,822 0,822
8
D
вт
м 0,210 0,240
9 D
0
м 0,401 0,401
10
D
л.п
м 0,441 0,441
11
D
л.ос
м 0,221 0,205
12 C
0
м/с 62,53 60,70
13 Р
0
МПа 4,897 6,055
14 Р
2
МПа 5,686 6,953
15
ρ
2
кг/м
3
41,36 47,71
16
z
лп
шт. 5 5
17
z
л.ос
шт. 4 8
18
s
r
м 0,00053 0,00053
19
µ
лп
- 0,7 0,7
20
µ
лос
- 0,7 0,7
Примечание. Диаметр уплотнений на покрывающем диске для обеих
колес находится как
0.
1,1 DD
пл
⋅
=
, а диаметры уплотнений у основных дисков
колес задаются на основании выполненного эскиза продольного разреза
проточной части компрессора.
154
Расчет осевой силы без учета протечек рабочего вещества через
лабиринтные уплотнения произведем в табл. 4.2. Предварительно найдем
вспомогательные величины.
Таблица 4.2
Осевое усилие без учета протечек
№ ступени
№
п/п
Параметр Размер-
ность
Расчет
1 2
1
(
)
2
.
2
ослвт
DD −
м
2
1-я ступень:
(
)
-0,0400,2210,210
22
=−
2-я ступень:
(
)
-0,0280,2050,240
22
=−
-0,040
-0,028
2
(
)
2
.
2
. ослпл
DD −
м
2
1-я ступень:
(
)
0,1460,2210,441
22
=−
2-я ступень:
(
)
0,1520,2050,441
22
=−
0,146
0,152
3
(
02
РР −
)
Па
1-я ступень:
(5,686-4,897)⋅10
6
=0,784⋅10
6
2-я ступень:
(6,953-6,062)⋅10
6
=0,893⋅10
6
0,784⋅10
6
0,893⋅10
6
4
F
0
Н 30656,0 135187,6
- для рабочего колеса 1-й ступени
()()
Н; 30656,062,53213
2
0,146
0,822
32
41,36555,0
100,7840,146
4
104,897(-0,040)
4
23244
2
2
66
0
2
.
2
.
2
2
2
2
02
2
.
2
.0
2
.
2
)1(0
=⋅−
−
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
⋅
−⋅⋅+⋅⋅=
=−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−−−−+−=
ππ
ρω
ππ
GC
DD
DРРDDРDDF
ослпл
ослплослвт
- для рабочего колеса 2-й ступени
Н. 135187,660,70213
2
0,152
0,822
32
47,71555,0
100,89390,152
4
106,055(-0,028)
4
2
2
66
)2(0
=⋅−
−
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
⋅
−⋅⋅+⋅⋅=
ππ
F
Проведем расчет дополнительных осевых сил, возникающих вследствие
наличия протечек сжимаемого газа у покрывающего и основного дисков.
Покрывающий диск 1-й ступени (протечки направлены к центру)
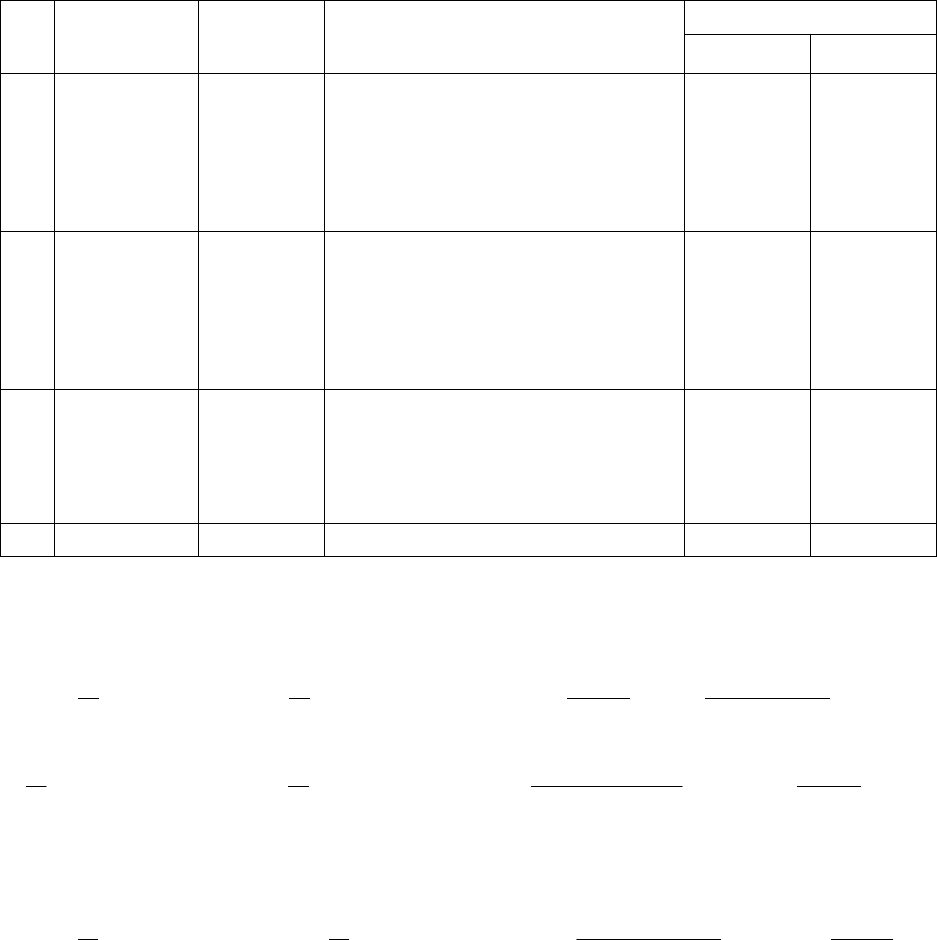
Определяем коэффициент протечек q решением уравнения (1.6) методом
последовательных приближений либо графическим способом (рис. 4.1).

155
()
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+−−
⋅
=∆
08,013,25,37,33700315,0
4
2
.
2
2
.
2
2
2
..
4
2.
2
2
2
2
)1(
D
D
D
D
qq
sD
Dz
D
Р
пл
Т
пл
Тпп
rплпл
пл
п
ψψ
µ
ρω
,
66
02)1(
100,784104,897)-5,686( ⋅=⋅=−=∆ РРР
п
Па;
()
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
−+⋅−⋅−
−
⋅⋅
⋅
=⋅
08,01
822,0
0,441
3,2645,05,3
822,0
0,441
645,07,337
0,000530,4417,0
822,06
00315,0
4
36,41822,0555
100,784
2
2
4
22
6
п
п
q
q
,
6211
100,784172163 59177629105,7809 ⋅=+⋅+⋅⋅
пп
qq
,
q
п
=0,0009789.
Рассчитываем дополнительную силу
δ
F
п(1)
по формуле (1.4), для чего
найдем коэффициенты этого уравнения.
19,889252
822,0
0,441
776
822,0
0,441
640252776640
2
2
.
2
2
.
=+
⎟
⎠
⎞
⎜
⎝
⎛
⋅−
⎟
⎠
⎞
⎜
⎝
⎛
⋅=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅=
D
D
D
D
b
плпл
;
7,5066,82
822,0
0,441
258
822,0
0,441
2206,82258220
2
2
.
2
2
.
=+
⎟
⎠
⎞
⎜
⎝
⎛
⋅−
⎟
⎠
⎞
⎜
⎝
⎛
⋅=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅=
D
D
D
D
c
плпл
;
0,8058291,1
822,0
0,441
575,1
822,0
0,441
25,1291,1575,125,1
2
2
.
2
2
.
=+
⎟
⎠
⎞
⎜
⎝
⎛
⋅−
⎟
⎠
⎞
⎜
⎝
⎛
⋅=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅=
D
D
D
D
t
плпл
;
()
()
Н. ,172740009789,0506,7645,0889,19
16
36,41822,0555
16
8058,0
42
2
2
4
2
2
)1(
=⋅−⋅⋅
⋅⋅
=
=⋅−⋅⋅
⋅⋅
=
t
пТп
qcb
D
F
ψ
ρω
δ
Покрывающий диск 2-й ступени (протечки направлены к центру)
Определяем коэффициент протечек q
п
также из уравнения (1.6) (рис. 4.1).
66
02)2(
100,893106,062)-6,955( ⋅=⋅=−=∆ РРР
п
;
()
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
−+⋅−⋅−
−
⋅⋅
⋅
=⋅
08,01
822,0
0,441
3,2645,05,3
822,0
0,441
645,07,337
0,000530,4417,0
822,06
00315,0
4
47,71822,0555
100,893
2
2
4
22
6
п
п
q
q
,
6211
100,893198595 68263169106,6684 ⋅=+⋅+⋅⋅
пп
qq
,
q
п
=0,0009705.
Рассчитываем дополнительную силу
δ
F
п(2)
по формуле (1.4).
Коэффициенты b, c, t для 2-й ступени равны соответствующим
коэффициентам 1-й ступени, поскольку отношение
2.
/ DD
пл
одинаково для
обеих ступеней.
()
Н. ,883320,0009705501,7645,0866,19
16
71,47822,0555
8058,0
42
)2(
=⋅−⋅⋅
⋅⋅
=
п
F
δ

156
Основной диск 1-й ступени (протечки направлены от центра)
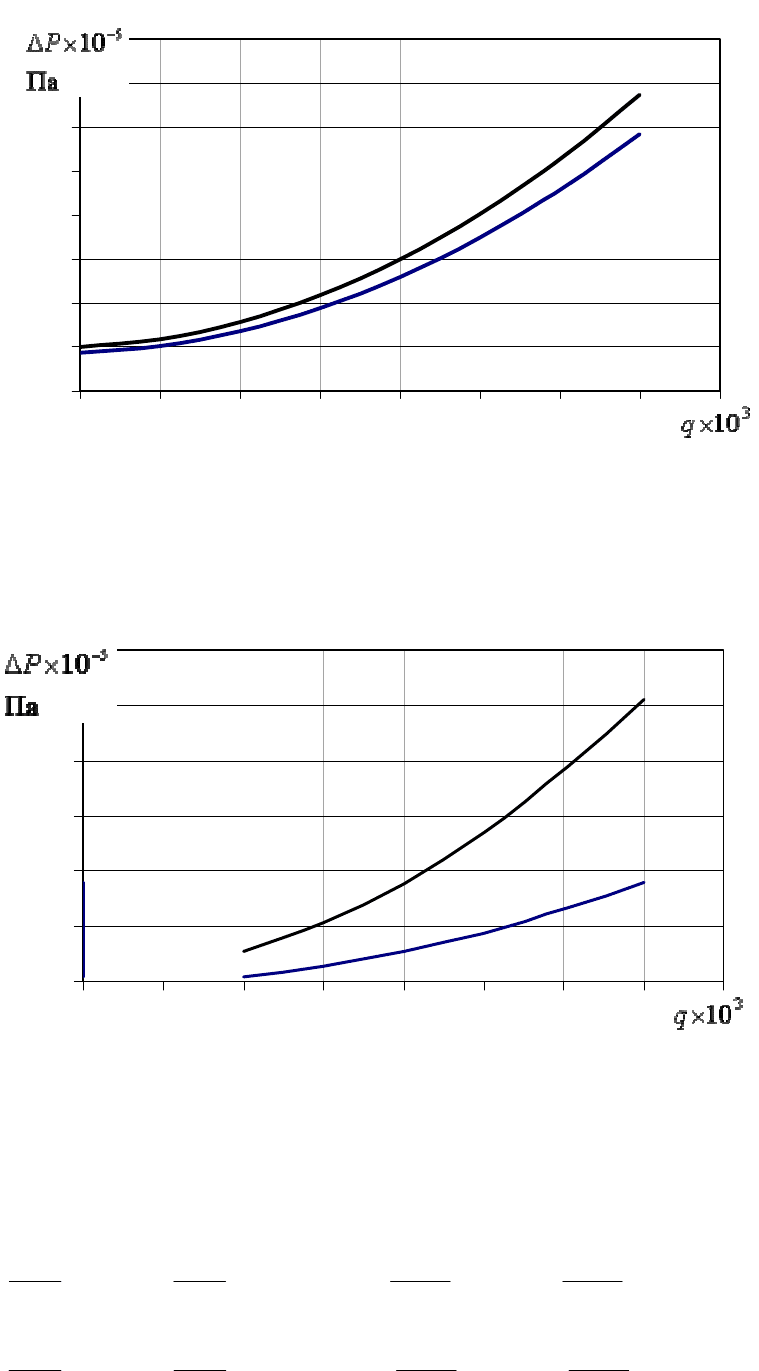
Определяем коэффициент протечек q решением уравнения (1.5) методом
последовательных приближений либо графическим способом (рис. 4.2).
()
()
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−+
⋅
=∆ 141,0125,000315,0
4
2
2
2
.
244,02
2
..
4
2.
2
2
2
2
)1(
D
D
qq
sD
Dz
D
Р
осл
осос
rослосл
осл
ос
µ
ρω
,
56
2'0)1(
100,377105,685)-6,062( ⋅=⋅=−=∆ РРР
ос
;
()
()
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−+
+
⋅⋅
⋅
⋅⋅
=⋅
1
822,0
0,221
41,0125,0
0,000530,2217,0
822,04
00315,0
4
41,36822,0555
100,377
2
2
244,0
2
2
4
22
5
ос
ос
q
q
,
5244,0212
100,377249637-818808101,8415 ⋅=⋅+⋅⋅
осос
qq
,
q
ос
= 0,00052.
Рассчитываем дополнительную силу
δ
F
ос(1)
по уравнению (1.3), для чего
найдем коэффициенты этого уравнения.
0,46560,000523045,03045,0
=
⋅
+
=
⋅+=
ос
qa
;
0,2197
882,0
0,221
185,017,0185,017,0
2
.
=⋅+=⋅+=
D
D
n
осл
.
Н. -29817,31
822,0
0,221
0,000520,4656
16
41,36822,0555
1
16
2
2197,0
42
2
2
.
2
4
2
2
)1(
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
⋅⋅
⋅⋅
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅⋅
⋅⋅
=
D
D
qa
D
F
осл
n
осос
ρω
δ
Основной диск 2-й ступени (протечки направлены к центру)
Определяем коэффициент протечек q решением уравнения (1.6) методом
последовательных приближений либо графическим способом (рис. 4.2).
()
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+−−=∆ 08,013,25,37,33700315,0
4
2
.
2
2
.
2
2
2
..
4
2.
2
2
2
2
)2(
D
D
D
D
qq
sD
Dz
D
Р
осл
Т
осл
Тосос
rослосл
осл
ос
ψψ
µ
ρω
;
66
2)2(
101,988104,967)-6,955( ⋅=⋅=−=∆
нос
РРР
;
()
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
−+⋅−⋅−
−
⋅⋅
⋅
=⋅
08,01
822,0
0,205
3,2644,05,3
822,0
0,205
644,07,337
0,000530,2057,0
822,08
00315,0
4
47,71822,0555
101,988
2
2
4
22
6
ос
ос
q
q
,
6211
101,988198595 -191875351104,9375 ⋅=+⋅+⋅⋅
осос
qq
,
q
ос
=0,000583.
157
0
2
4
6
8
10
12
14
16
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6
1
2
Рис. 4.1. Зависимость перепада давлений в зазоре между покрывающим
диском и корпусом от коэффициента протечек: 1 – первая ступень, 2 – вторая
ступень
0
20
40
60
80
100
120
0,0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6
1
2
Рис. 4.2. Зависимость перепада давлений в зазоре между основным
диском и корпусом от коэффициента протечек: 1 – первая ступень, 2 – вторая
ступень
Рассчитываем дополнительную силу
δ
F
ос(2)
по формуле (1.4).
98,278252
822,0
0,205
776
822,0
0,205
640252776640
2
2
.
2
2
.
=+
⎟
⎠
⎞
⎜
⎝
⎛
⋅−
⎟
⎠
⎞
⎜
⎝
⎛
⋅=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅=
D
D
D
D
b
ослосл
;
31,9406,82
822,0
0,205
258
822,0
0,205
2206,82258220
2
2
.
2
2
.
=+
⎟
⎠
⎞
⎜
⎝
⎛
⋅−
⎟
⎠
⎞
⎜
⎝
⎛
⋅=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅=
D
D
D
D
c
ослосл
;
158
0,9760291,1
822,0
0,205
575,1
822,0
0,205
25,1291,1575,125,1
2
2
.
2
2
.
=+
⎟
⎠
⎞
⎜
⎝
⎛
⋅−
⎟
⎠
⎞
⎜
⎝
⎛
⋅=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅=
D
D
D
D
t
ослосл
;
()
()
Н. 9193,20,000583940,31645,0278,98
16
47,71822,0555
16
9760,0
42
2
2
4
2
2
)2(
=⋅−⋅⋅
⋅⋅
=
=⋅−⋅⋅
⋅⋅
=
t
осТос
qcb
D
F
ψ
ρω
δ
Результаты расчета дополнительных сил сведем в табл. 4.3. В ней же
приведем расчет суммарных осевых усилий для 1-й и 2-й ступеней и общего
осевого усилия, действующего на ротор компрессора.
Таблица 4.3
Суммарные осевые усилия
№ ступени
№
п/п
Параметр Размер-
ность
Расчет
1 2
1
δ
F
п
Н
7274,1 8332,8
2
δ
F
ос
Н
-29817,3 9193,2
3
Σ
F
Н
67747,4
(-29817,3)-7274,130656,0
)1()1()1(0)1(
=
=+=
=
+
+
=
Σ осп
FFFF
δ
δ
134327,2
9193,2-8332,8135187,6
)2()2()2(0)2(
=
=+=
=
+
+
=
Σ осп
FFFF
δ
δ
67747,4
134327,2
4
)(к
F
Σ
Н
202074,6134327,2
67747,4
)2()1()(
=+
+
=
+
=
ΣΣΣ
FFF
к
202074,6
Определение размеров думмиса
Расчетная схема упорного подшипника показана на рис. 1.2. Рассчитаем
осевое усилие, которое будет воспринимать упорный подшипник. Для этого
зададимся удельным давлением масла на упорную колодку подшипника
Р
уд
= 1,0 МПа и определим размеры упорных колодок.
Число колодок упорного подшипника примем
z
к.уп
=10.
Диаметр опорной поверхности вала
м, 141,0
50555
15,55
][
5
3
3
=
⋅
⋅
=
⋅
⋅
=
кр
в
ш
N
d
τω
где
мощность на валу компрессора N
в
= 15,5 МВт – из газодинамического
расчета компрессора; [
τ
кр
] = 50 МПа – допускаемое напряжение кручения
для стали 30ХГСА.

159
Внутренний радиус колодок упорного подшипника
0705,02/
1
=
≈
ш
dR
м.
Радиальный размер колодок упорного подшипника
05,0705,071,071,0
1
=
⋅
=
⋅
≈
Rb
уп
м.
Наружный радиус колодок упорного подшипника
121,005,00705,0
12
=
+
=
+
=
уп
bRR
м.
Средний радиус колодок
0,0958)121,00705,0(5,0)(5,0
21
=
+
⋅
=
+⋅
=
RRR
ср
.
Углом сектора колодки задаемся:
θ
= 0,5 рад (28,65°).
Средний окружной размер упорных колодок
0,04790,50,0958
=
⋅
=⋅
=
θ
сруп
Rl
м.
Осевое усилие, воспринимаемое упорным подшипником:
23950100,050,0479100,1
5
.
=⋅⋅⋅⋅=⋅⋅⋅=
упкупупудуп
zblРF
Н.
Для определения максимального повышения температуры масла в
подшипнике воспользуемся эмпирической формулой [6], для чего зададимся
относительным расстоянием до опорного ребра подушки
упр
l
.
=0,55 и найдем
окружную скорость центра упорного подшипника
53,170,0958555 =
⋅
=⋅=
ср
RU
ω
м/с.
[
]
[]
С. 13,04100,1)5,055,0(8,2114
)5,0(8,2114
517,530015,0
.
0015,0
max.
°=⋅⋅−⋅−⋅⋅=
=⋅−⋅−⋅⋅=∆
⋅
⋅
e
Рlet
удупр
U
м
Температуру масла на сливе из подшипника задаем
t
м.к
= 50 °С.
Температура масла при подаче в подшипник
52,1314,5304,05004,0
..
=
⋅
+
=
⋅+
=
Utt
кмнм
°С.
Максимальная температура масла
65,1704,1313,52
max..max.
=
+
=
∆
+
=
мнмм
ttt
°С.
Максимальная температура масла в подшипнике не превышает
предельно допустимую температуру
120][17,65
max.max.
=
<
=
мм
tt
°C.
Осевое усилие, воспринимаемое думмисом:
1781223950-20207
=
=
−
=
Σ упдум
FFF
Н.
Давление перед думмисом
Па. 106,664
822,0
0,205
1
8
47,71228,2
106,9551
8
6
2
22
6
2
)2(2
2
)2(.)2(2
2
)2(2
)2(2
⋅=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⋅
−⋅=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⋅
−=
D
DU
РР
осл
дум
ρ
