Ваняшов А.Д., Кустиков Г.Г. Учебное пособие для курсового проектирования - Расчет и конструирование центробежных компрессорных машин
Подождите немного. Документ загружается.

110
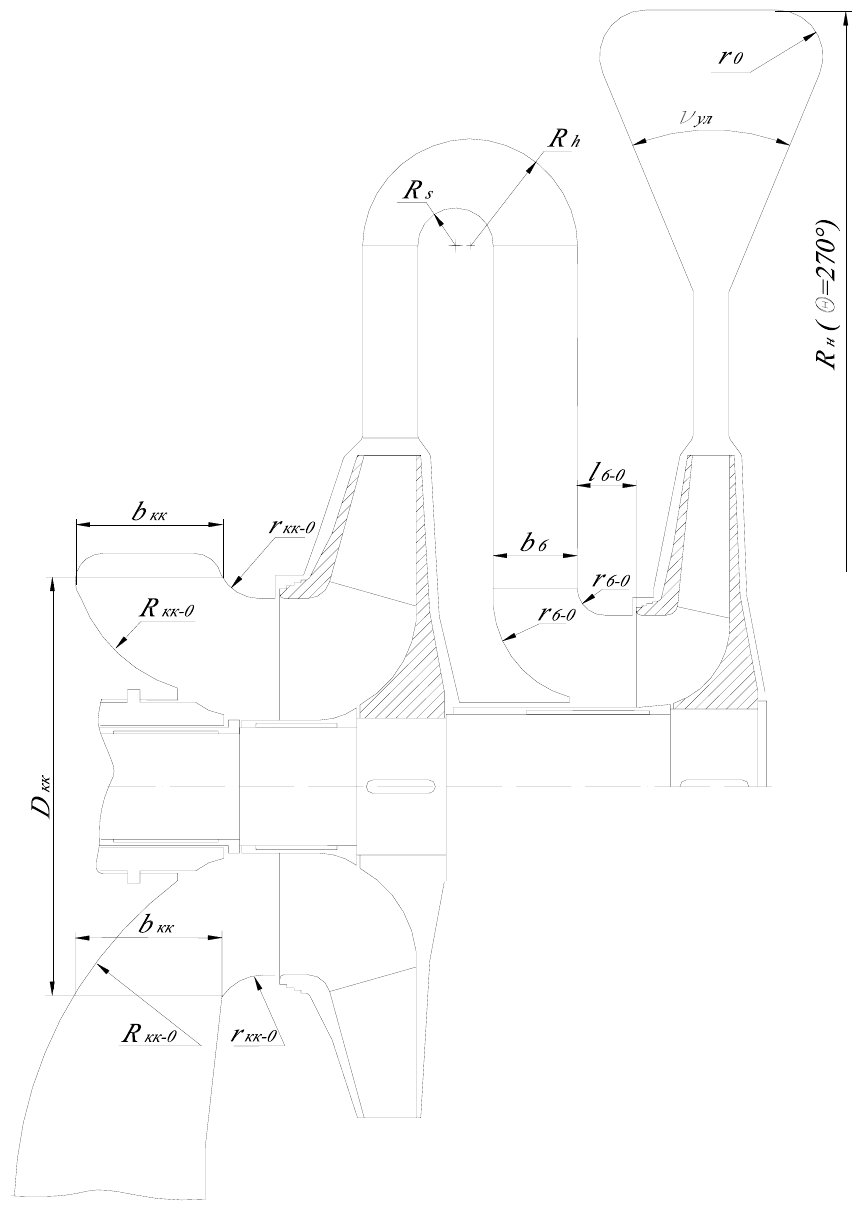
Рис. 1.10. Схема конструктивных размеров всасывающей камеры и
обратного направляющего аппарата в меридиональной плоскости
111
1.3.4. Конструирование всасывающей камеры
В меридиональной плоскости определяются ширина кольцевого
конфузора b
кк
, радиусы внутреннего r
кк-0
и внешнего R
кк-0
поворотов от
сечения к-к (кольцевой конфузор) к сечению 0-0 (вход в колесо первой
ступени).
Задается внутренний радиус поворота (для всасывающей камеры первой
секции задаются по возможности большие значения, а для всасывающих
камер последующих секций – из конструктивных возможностей):
кккк
br
⋅
−
≥
−
)6,03,0(
0
.
Задается коэффициент конфузорности (К
кк-0
=С
кк
/С
0
):
К
кк-0
= 1,1 – 2,0.
Радиус внешнего поворота [8]
∆+=
−−
кк
кк
кк
кк
b
r
b
R
00
,
где
)(
))(/(2
00
22
000
2
00
вткк
вткккккк
DDК
DDbrКDD
+⋅
−⋅⋅++
=∆
−
−−
.
Ширина и диаметр кольцевого конфузора
)(
00
2
вткккк
DDАКААb −⋅⋅++−=
−
,
где
∆+
+
=
−
4)/(8
)(
0 кккк
втн
br
DD
А
;
∆
⋅
+
+
−
=
− кккквткк
brDDD
00
2)(5,0
.
2. Прочностные расчеты элементов компрессора
К числу прочностных расчетов относятся расчеты, связанные с
определением несущей способности элементов конструкции центробежного
компрессора: расчет критической частоты вращения ротора; расчет
напряжений в основном и покрывающем дисках колес, лопатках, заклепках
лопаток; расчет шпонок вала, диаметра болтов и шпилек горизонтального
разъема и т. д.
2.1. Расчет дисков рабочего колеса на прочность
Сущность расчета на прочность основного и покрывающего дисков
рабочего колеса заключается в оценке радиальных и тангенциальных
напряжений, возникающих в характерных сечениях дисков от действия
центробежных сил и сравнения этих напряжений с допускаемыми.
112
Расчеты на прочность достаточно выполнить для самого широкого
рабочего колеса компрессора, т.к. напряжения там будут наибольшими.
Допущения, принятые в приводимых ниже расчетных методиках:
1) температура не меняется ни по толщине, ни по радиусу диска;
2) не учитываются напряжения изгиба от вибрации и внешних нагрузок;
3) радиальные напряжения распределены симметрично относительно
оси
вращения.
Основной и покрывающий диски колеса относятся к дискам сложной
формы, т.к. представляют собой комбинацию дисков простых форм, к
которым относятся:
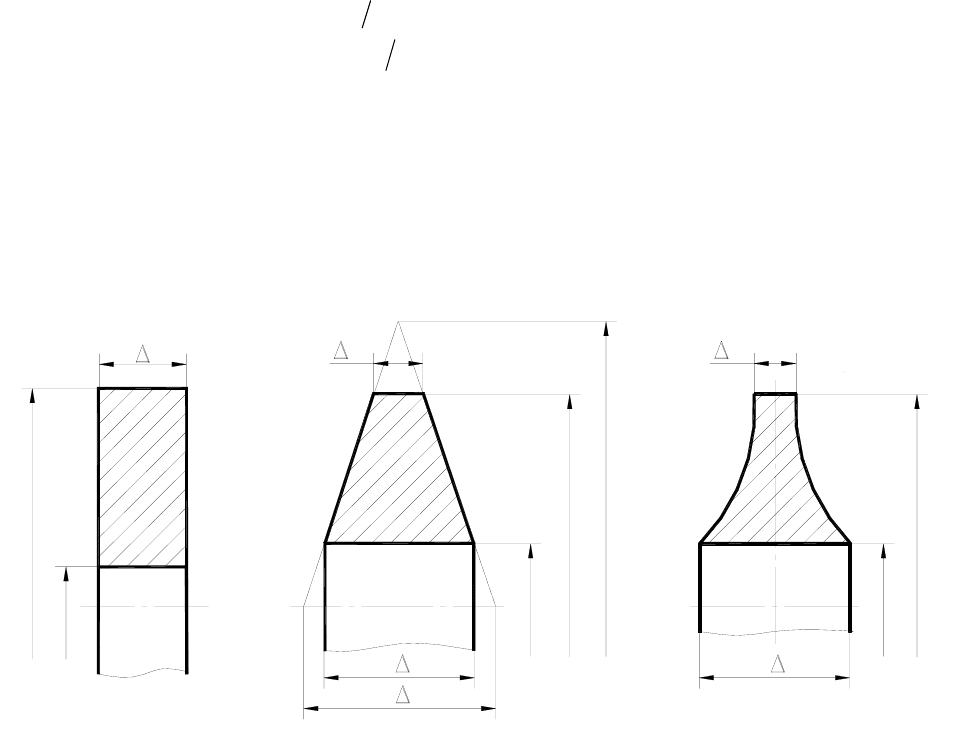
- диски постоянной толщины
const
=
∆
(рис. 2.1 а);
- конические диски
)1(
0 к
RR
−
∆=∆
(рис. 2.1 б);
- гиперболические диски
m
Rconst=∆
, где m – показатель степени (рис. 2.1 в).
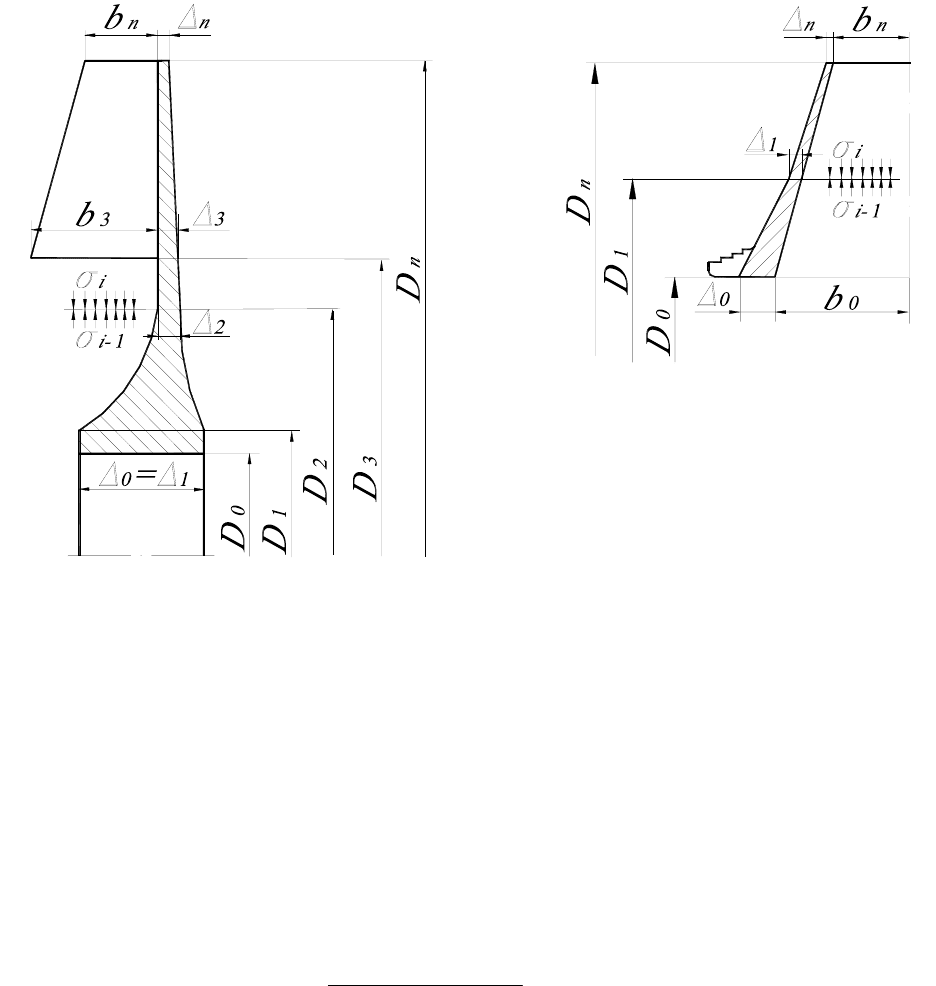
Поэтому при расчетах на прочность реальные диски сложного профиля
разбивают на несколько участков, имеющих простые формы (рис. 2.2).
Напряжения в дисках сложного профиля рассчитывают методом «двух
расчетов». Ниже приведем порядок расчета по этому методу.
R1
R2
2
R2
R1
Rк
1
0
R1
R2
2
1
а) б) в)
Рис. 2.1. Основные формы дисков: а) постоянной толщины; б) конический;
в) гиперболический
113
а) б)
Рис. 2.2. Расчетные схемы к определению напряжений в основном (а) и
покрывающем (б) дисках
Первый расчет
В первом расчете напряжения обозначаются одним штрихом (
σ′
r
,
σ′
t
).
Формируются граничные условия на начальном диаметре. Для этого
задаются значениями радиальных напряжений
σ′
r0
на диаметре D
0
диска. Для
основного диска радиальные напряжения на диаметре D
0
определяются
удельным давлением на посадочном диаметре. Ориентировочно можно
принимать
σ′
r0
= − (5-10) МПа [13] либо рассчитывать по формуле
fnbD
Nk
q
об
в
⋅⋅⋅⋅
⋅
⋅
=
0
2
0
2
60
π
,
где N
в
– мощность на валу компрессора, МВт; n
об
– число оборотов, об/мин;
k – коэффициент запаса (k = 1,5 – 2,0); f – коэффициент трения (f=0,15-0,2).
Для покрывающего диска радиальные напряжения на диаметре D
0
отсутствуют, поэтому
σ′
r0
= 0.
Задаются произвольными значениями тангенциальных напряжений
σ′
t0
на начальном диаметре D
0
диска.
Вычисляются напряжения
σ′
r
и
σ′
t
на наружной поверхности каждого
участка по формулам, которые в общем виде записываются следующим
образом:
)1()1()1()()1()()1( +++++
⋅
+
⋅
′
+
⋅
′
=
′
iciititiririr
T
α
α
σ
α
σ
σ
, (2.1)
)1()1()1()()1()()1( +++++
⋅
+
⋅
′
+
⋅
′
=
′
iciititiririt
T
β
β
σ
β
σ
σ
, (2.2)

114
где
α
r
,
α
t
,
α
c
, β
r
, β
t
, β
c
– коэффициенты, зависящие от соотношения
диаметров (D
i
/D
i+1
) .
Коэффициенты эти даны в номограммах, которые впервые были
составлены В.Ф. Рисом, либо по формулам (см. ниже).
Параметр, учитывающий действие центробежной силы:
13
2
)1(
101
)(
⋅
⋅
=
+ обi
nD
Т
, или
2
13
101
)(
⋅
⋅
=
обк
nD
Т
,
где D
(i+1)
– наружный диаметр рассматриваемого участка (гиперболического
или постоянной толщины), мм; D
к
– диаметр полного конуса для конических
участков, мм; n
об
– число оборотов, об/мин.
Диаметр полного конуса конических участков, например, для рис. 2.1 б,
находится по формуле
)(
12
21
1
1
DDDD
к
−
∆−∆
∆
+=
.
Таким образом находятся напряжения на наружной поверхности
последнего участка
σ′
rп
и
σ′
tп
.
Очевидно, что полученное значение радиального напряжения на
диаметре D
п
не будет удовлетворять второму граничному условию, согласно
которому
σ
rп
=0 (для основного и покрывающего дисков), т.к. напряжение
σ′
t0
было выбрано произвольно. Далее выполняется второй расчет.
Второй расчет
Во втором расчете напряжения обозначаются двумя штрихами (
σ′′
r
,
σ′′
t
).
Задаются значением радиального напряжения на начальном диаметре
для основного и покрывающего дисков
σ′′
r0
= 0, а напряжение
σ′′
t0
снова
выбирают произвольно. Причем напряжения в сечениях дисков находят,
полагая, что диск неподвижен, т.е. n
об
= 0. В этом случае центробежные силы
на диск не действуют, а напряжения в сечениях диска возникают из-за
приложенного на диаметре D
0
напряжения
σ′′
t0
.
Выполняются расчеты напряжений по формулам (2.1), (2.2) при новых
граничных условиях.
Итогом второго расчета будут новые значения радиальных и
тангенциальных напряжений (
σ′′
rп
,
σ′′
tп
) на наружной поверхности диска. В
этом случае опять
σ
rп
≠ 0.
Расчет действительных напряжений
Действительные напряжения на любом диаметре:
)()()( iririr
σ
ϕ
σ
σ
′
′
⋅
+
′
=
,
)()()( ititit
σ
ϕ
σ
σ
′
′
⋅
+
′
=
,
где φ – поправочный коэффициент, который определяется из граничных
условий на внешнем диаметре D
п
.
rпrпrп
σσσϕ
′′′
−= )(
,

115
а т.к.
σ
rп
= 0, то
rп
rп
σ
σ
ϕ
′′
′
−=
.
Выявляются максимальные значения напряжений в различных сечениях
диска
max
)(ir
σ
и
max
)(it
σ
, которые затем сравниваются с допускаемыми для
данного материала:
{
}
max
)(
max
)(
max
;max
itir
σσσ
=
,
[]
σσ
≤
max
.
Допускаемое напряжение определяют по формуле
{
}
ввтт
;min][ nn
σ
σ
σ
=
,
где
σ
т
,
σ
в
,– минимальные значения пределов текучести и прочности при
расчетной температуре; п
т
, п
в
- коэффициенты запаса прочности по пределам,
соответственно, текучести п
т
=1,5; прочности п
в
= 2,4.
Значения пределов текучести и прочности для различных материалов
даны в табл. 2.1.
Определение коэффициентов
α
r
,
α
t
,
α
c
, β
r
, β
t
, β
c
Приведенные ниже значения коэффициентов
α
c
и β
c
получены для
стальных дисков, для которых коэффициент Пуассона
µ
=0,3; модуль
упругости Е=2·10
11
Па; плотность ρ
ст
=8000 кг/м
3
. Если диск изготовлен не из
стали, а из другого материала, коэффициенты
α
c
и β
c
необходимо умножить
на отношение плотностей ρ
м
/ρ
ст
, где ρ
м
– плотность материала.
Диски постоянной толщины
2))/(1(
2
)1()(
+
+==
iitr
DD
βα
;
2))/(1(
2
)1()( +
−==
iirt
DD
βα
;
))/(7,0)/(6,23,3(4,27
4
)1()(
2
)1()(
++
⋅−⋅−⋅−=
iiiic
DDDD
α
;
))/(7,0)/(6,29,1(4,27
4
)1()(
2
)1()(
++
⋅+⋅−⋅−=
iiiic
DDDD
β
.
Для гиперболических и конических дисков значения коэффициентов
α
r
,
α
t
,
α
c
, β
r
, β
t
, β
c
берутся из номограмм, которые даны на рис. 2.3 – 2.14 [13,
20-22].
Для конических участков дисков коэффициенты
α
r
,
α
t
,
α
c
, β
r
, β
t
, β
c
в
номограммах представлены функцией двух аргументов:
к
i
D
D
t
)(
1
=
и
к
i
D
D
t
)1( +
=
.
Для гиперболических участков дисков коэффициенты
α
r
,
α
t
,
α
c
, β
r
, β
t
,
β
c
в номограммах также даются в виде функции двух аргументов:
)1(
)(
+
=
i
i
D
D
x
и
)(
)1(
i
i
z
∆
∆
=
+
.
116
Таблица 2.1
Механические свойства материалов при
t = 20 °C
Стали
Марка 30Х 35Х 50Х 30ХМА 20ХГСА 30ХГС 30ХН3А 38Х2Ю
термооб
работка
Т11 Т11 Т12 Т13 Т13 Т13 Т12 азотиро-
вание
σ
Т
,
МПа
690 740 880 740 640 830 780 780
σ
В
,
МПа
880 910 1080 930 780 1080 980 930
НВ 187 197 229 229 207 229 241 260
Примечание. Т11 – закалка t = 860 °C, охлаждение в масле; отпуск t = 500 °C,
охлаждение в масле или воде; Т12 – закалка
t = 830 °C, охлаждение в масле;
отпуск
t = 520 °C, охлаждение в масле или воде; Т13 – закалка t = 880 °C,
охлаждение в масле; отпуск
t = 54 °C, охлаждение в масле или воде.
Алюминиевые сплавы
Марка АЛ2 АЛ4 АЛ8 АЛ9 АЛ10В АЛ19
термооб-
работка
Т2 Т1 Т6 Т4 Т2 Т4 Т5 Т1 Т4 Т5
σ
Т
,
МПа
- - - - - - - - - -
σ
В
,
МПа
157 196 235 284 137 186 196 167 294 333
НВ 50 70 70 60 45 50 60 90 70 90
ρ, кг/м
3
2650 2650 2650 2650 2650 2650
Примечание. Т1 – искусственное старение без предварительной закалки; Т2 –
отжиг; Т4 – закалка; Т5 – закалка и неполное искусственное старение; Т6 –
закалка и полное искусственное старение.
Титановые сплавы
Марка ВТ1-0 ВТ1-00 ВТ3-1 ВТ5
σ
Т
,
МПа
340 240 830 590
σ
В
,
МПа
390 310 930 690
НВ 130 130 260 26
ρ, кг/м
3
4520 4520 4500 4400

117
Для участков дисков, на которых расположены лопатки, необходимо
ввести поправку к коэффициентам
α
c
и β
c
, которая учитывает появление
дополнительной центробежной силы от приложенной к диску массы лопаток.
Приближенно считается, что нагрузки от этих дополнительных
центробежных сил воспринимаются только диском [21]. При этом лопатки
заменяют некоторой массой, равномерно распределенной по поверхности
диска. Влияние этой массы на добавочную центробежную силу и,
следовательно, на напряжение в материале диска может
быть учтено
условным увеличением плотности материала диска для данного участка.
Приведенная плотность материала диска, кг/м
3
:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∆⋅⋅
⋅⋅⋅
+⋅=
D
zbk
нб
мпр
π
δ
ρρ
.
1
, (2.3)
где δ – толщина лопатки, мм; b – высота лопаток, мм; ∆ – толщина диска; D –
диаметр сечения диска, мм; z – число лопаток; k
б.н
– коэффициент боковой
нагрузки, принимаемый для основного диска k
б.н
= 0,7, для покрывающего
диска k
б.н
= 0,3.
По формуле (2.3) рассчитывается приведенная плотность для начального
и конечного сечений участка, а затем находится средняя для участка с
боковой нагрузкой приведенная плотность
2
)1()(
.
+
+
=
iпрiпр
српр
ρ
ρ
ρ
.
Для колеса с двухсторонним всасыванием
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∆⋅⋅
⋅⋅⋅⋅
+⋅=
D
zbk
нб
мпр
π
δ
ρρ
.
2
1
.
Коэффициенты с учетом боковой нагрузки от лопаток
м
српр
сс
ρ
ρ
αα
.
⋅=
′
;
м
српр
сс
ρ
ρ
ββ
.
⋅=
′
.
118
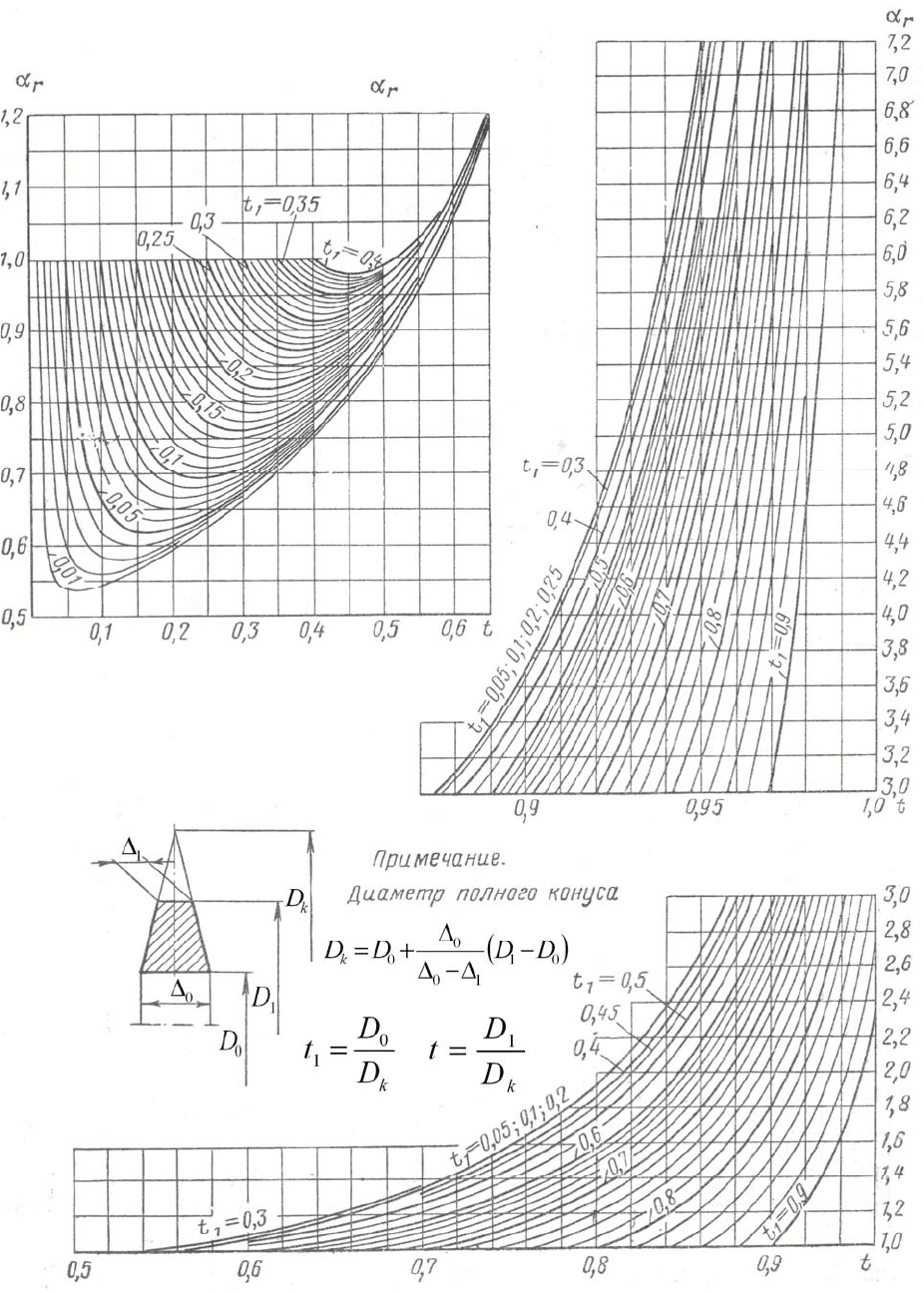
Рис. 2.3. Номограмма для определения коэффициента
α
r
у конических дисков
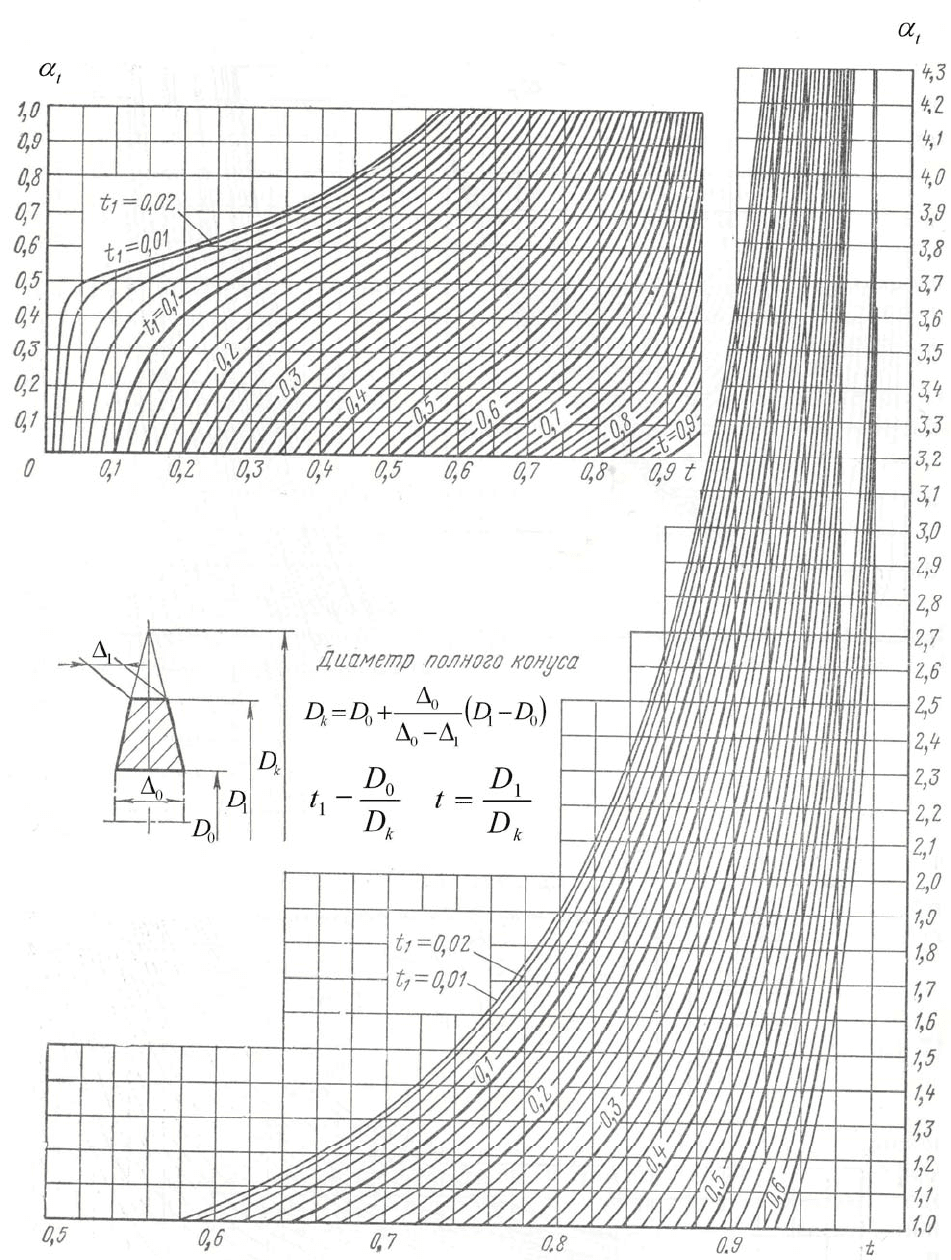
119
Рис. 2.4. Номограмма для определения коэффициента
α
t
у конических дисков
