Трушков А.С. Учебно-методический комплекс по дисциплине Компьютерное моделирование
Подождите немного. Документ загружается.

51
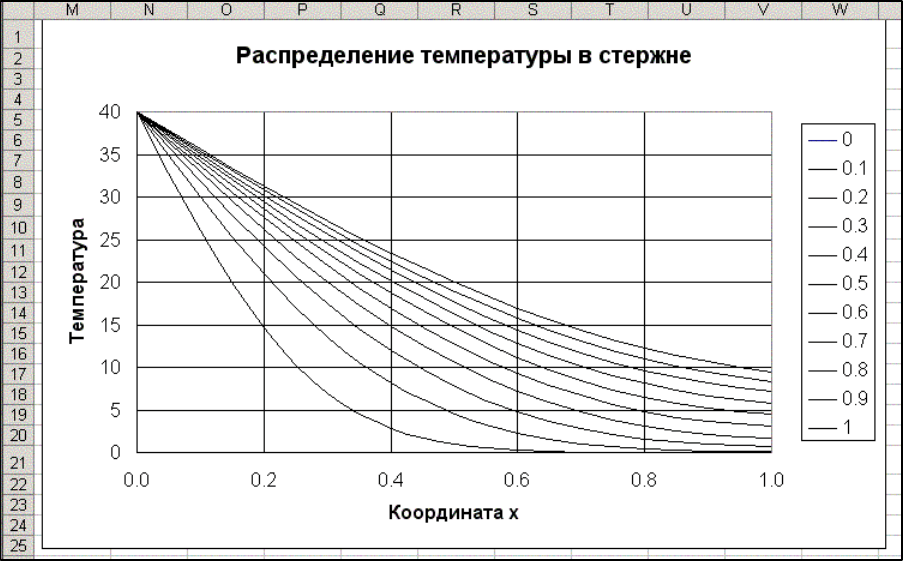
Рис. 6.

52
Лабораторная работа № 4
"Моделирование колебаний упругой струны"
Типичным примером дифференциального уравнения в частных произ-
водных второго порядка гиперболического типа является уравнение колебаний
струны длиной l под действием внешней переменной силы в течении времени
Т. Считаются заданными начальные перемещения
ϕ
ϕϕ
ϕ
(х) и скорости
ψ
ψψ
ψ
(х) в каж-
дой точке струны. Принимается, что заданы зависимости перемещений от вре-
мени u
n
(t)
и u
k
(t)
на концах струны:
),t,x(fuau
xx
2
tt
+
++
+
′
′′
′′
′′
′
=
==
=
′
′′
′′
′′
′
[
[[
[
]
]]
]
,l,0x),x()0,x(u
∈
∈∈
∈
=
==
=
ϕ
ϕϕ
ϕ
[
[[
[
]
]]
]
,l,0x),x()0,x(u
t
∈
∈∈
∈
=
==
=
′
′′
′
ψ
ψψ
ψ
[
[[
[
]
]]
]
T,0t),t(u)t,l(u),t(u)t,0(u
kn
∈
∈∈
∈
=
==
=
=
==
=
Пусть на одном из концов струи заданы граничные условия в форме гар-
монических перемещений по закону
(
((
(
)
))
)
tcosA)t(u
k
ν
νν
ν
=
==
=
. Теоретические значения
резонансных частот струны равны
l
ma
i
π
ππ
π
ν
νν
ν
=
==
= . Если
i
ν
νν
ν
ν
νν
ν
=
==
=
, то наступает явление
резонанса.
Целью работы является изучение различных режимов колебаний, соот-
ветствие теоретических резонансных частот их фактическим значениям, полу-
ченным в вычислительном эксперименте, графическое представление колеба-
ний струны в режиме биений, модуляций, резонанса.
53
Лабораторная работа № 5
"Решение и моделирование задач линейного программирования"
Пример выполнения лабораторной работы
Исследовать задачу линейного программирования с помощью пакета про-
грамм "Компьютерное моделирование".
1) Решение детерминированной задачи.
min z = 4x
1
+ x
2
3x
1
+ x
2
= 3
4x
1
+ 3x
2
≥
≥≥
≥
6
x
1
+ 2x
2
≤
≤≤
≤
4
x
i
≥
≥≥
≥
0
Стандартная форма ЗЛП:
min z = 4x
1
+ x
2
3x
1
+ x
2
= 3
4x
1
+ 3x
2
- x
3
= 6
x
1
+ 2x
2
+ x
4
= 4
x
i
≥
≥≥
≥
0
Вводим фиктивные переменные для начала вычислений симплекс-
методом:
min z = 4x
1
+ x
2
+Mx
4
+Mx
5
,
3x
1
+ x
2
+ x
4
= 3
4x
1
+ 3x
2
- x
3
+ x
5
= 6
x
1
+ 2x
2
+ x
6
= 4
x
i
≥
≥≥
≥
0
Решение ЗЛП, полученное с помощью программы:
x
1
= 0.4, x
2
= 1.8, z = 3.4.
2) Считая, что уровень неопределенности исходных данных составляет
β
ββ
β
= 0.05 провести статистическое моделирование для заданной модели при чис-
ле этапов моделирования k = {10; 30; 100}. Повторить расчеты для уровней не-
определенности
β
ββ
β
= 0.1 и
β
ββ
β
= 0.2.
Результаты моделирования для целевой функции и исходных переменных
представить в таблицах, в которых представить для каждого из девяти расчет-
ных случаев выборочное среднее М, стандартную ошибку
σ
σσ
σ
, число этапов k
0
с
конечным оптимальным решением.
Для рассматриваемой задачи результаты
моделирования имеют вид.
Целевая функция
Параметры k = 10
k = 30
k =
100
M(z)
3,259 3,376 3,403
σ
σσ
σ(z)
0,397 0,354 0,358
β
ββ
β = 0,05
k
0
9 29 89
β
ββ
β
= 0,10
M(z)
3,747 3,488 3,456

54
σ
σσ
σ(z)
0,922 0,912 0,882
k
0
7 21 80
M(z)
4,066 3,899 4,009
σ
σσ
σ(z)
2,178 1,633 1,808
β
ββ
β = 0,20
k
0
5 21 54
Число k
0
этапов моделирования, в которых был достигнут оптимум целе-
вой функции, определяется по формуле:
k
0
= k - k
1
- k
2
,
где k - число проведенных этапов моделирования,
k
1
- число этапов, в которых получено недопустимое решение,
k
2
- число этапов, в которых получена неограниченная ОДР.
Исходная переменная х
1
Параметры k = 10
k = 30
k = 100
M(z)
0,378 0,379 0,395
σ
σσ
σ(z)
0,151 0,104 0,127
β
ββ
β = 0,05
k
0
9 29 89
M(z)
0,541 0,484 0,449
σ
σσ
σ(z)
0,258 0,291 0,449
β
ββ
β = 0,10
k
0
7 21 80
M(z)
0,838 0,636 0,779
σ
σσ
σ(z)
0,454 0,481 0,486
β
ββ
β = 0,20
k
0
5 21 54
Исходная переменная х
2
Параметры
k =
10
k =
30
k =
100
M(z)
1,750 1,871 1,823
σ
σσ
σ(z)
0,282 0,201 0,234
β
ββ
β = 0,05
k
0
9 29 89
M(z)
1,751 1,887 1,793
σ
σσ
σ(z)
0,520 0,521 0,481
β
ββ
β = 0,10
k
0
7 21 80
M(z)
1,010 1,665 1,445
σ
σσ
σ(z)
0,599 1,006 0,678
β
ββ
β = 0,20
k
0
5 21 54
Результаты моделирования показывают:

55
а) точечные оценки математических ожиданий
)f(M
значений оценивае-
мых параметров не зависят от числа этапов моделирования и группируются
около средних значений;
б) точечные оценки математических ожиданий целевой функции
)z(M
и
1-ой переменной
)x(M
1
увеличиваются с ростом неопределенности данных, то-
чечные оценки математических ожиданий 2-ой переменной
)x(M
2
при
β
ββ
β
= 0,2
существенно ниже, чем при
β
ββ
β
= 0,1 и
β
ββ
β
= 0,05;
в) точечные оценки средних квадратических отклонений оцениваемых
параметров не зависят от числа этапов моделирования и увеличиваются с рос-
том неопределенности данных;
г) с ростом неопределенности данных число этапов моделирования k
0
, в
которых найдено оптимальное решение, уменьшается.
3) Для доверительной вероятности
γ
γγ
γ
= 0,95 построить доверительные ин-
тервалы для целевой функции и исходных переменных для всех расчетных слу-
чаев по формулам:
f
н
= M( f ) -
δ
δδ
δ
- нижняя граница параметра f,
f
в
= M( f ) +
δ
δδ
δ
- верхняя граница параметра f,
0
k
)f(t
σ
σσ
σ
δ
δδ
δ
γ
γγ
γ
=
==
=
- полуширина доверительного интервала (погрешность точеч-
ной оценки),
t
γ
γγ
γ
- квантиль распределения Стьюдента, вычисляемый по встроенной
функции табличного процессора MS Excel:
t
γ
γγ
γ
= СТЬЮДРАСПОБР( 1 -
γ
γγ
γ
; k
0
) .
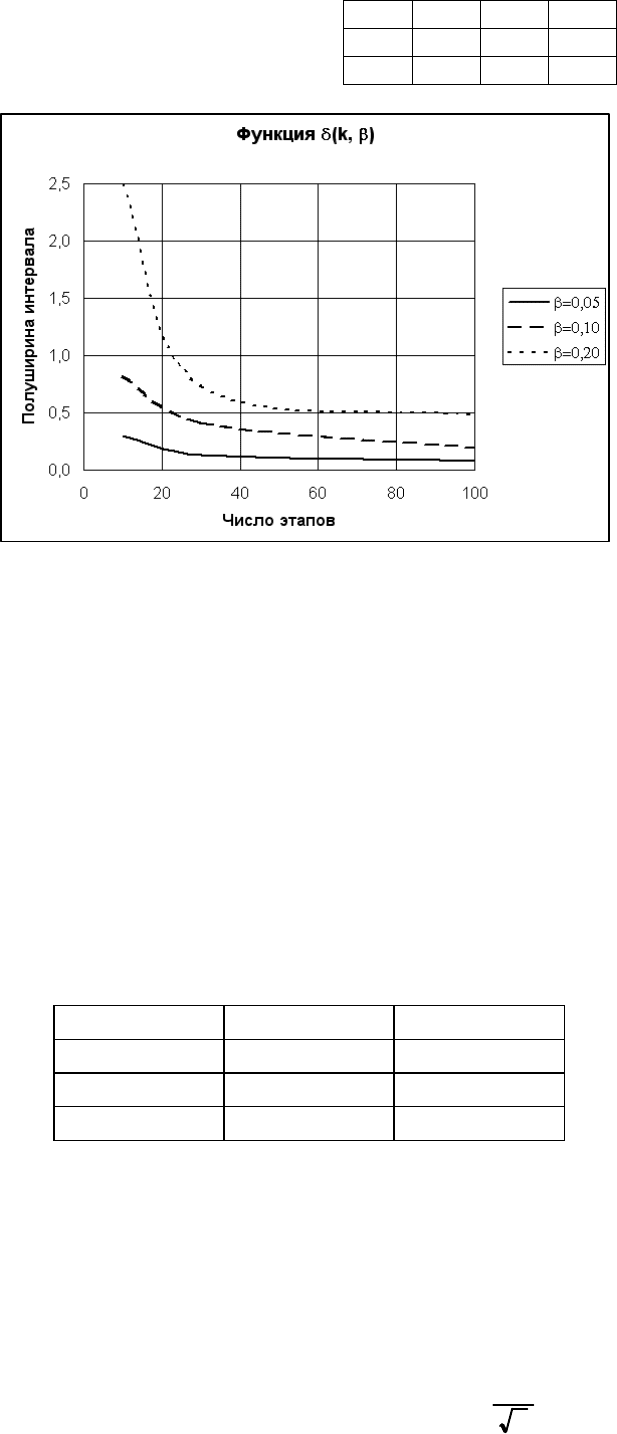
Расчеты целее сообразно провести в рабочих листах табличного процес-
сора MS Excel. Для целевой функции рассматриваемого примера рабочий лист
для расчета доверительных интервалов и график зависимости его полуширины
от числа этапов имитационного эксперимента и неопределенности данных при-
веден ниже.
Построение доверительного интервала для целевой функции
Математическое ожидание
Квантиль Стьюдента
k 10 30 100
k 10 30 100
β
ββ
β=0,05
3,259
3,376
3,403
β
ββ
β=0,05
2,262
2,045
1,987
β
ββ
β=0,05
3,747
3,488
3,456
β
ββ
β=0,05
2,365
2,080
1,990
β
ββ
β=0,05
4,066
3,899
4,009
β
ββ
β=0,05
2,571
2,080
2,001
Стандартная ошибка
Полуширина интервала
k 10 30 100
k 10 30 100
β
ββ
β=0,05
0,397
0,354
0,358
β
ββ
β=0,05
0,299
0,134
0,075
β
ββ
β=0,05
0,922
0,912
0,882
β
ββ
β=0,05
0,824
0,414
0,196
β
ββ
β=0,05
2,178
1,633
1,808
β
ββ
β=0,05
2,504
0,741
0,471
Частоты
Нижняя граница
k 10 30 100
k 10 30 100
β
ββ
β=0,05
9 29 89
β
ββ
β=0,05
2,960
3,242
3,328
β
ββ
β=0,05
7 21 80
β
ββ
β=0,05
2,923
3,074
3,260
β
ββ
β=0,05
5 21 59
β
ββ
β=0,05
1,562
3,158
3,538
Верхняя граница
k 10 30 100
56
β
ββ
β=0,05
3,558
3,510
3,478
β
ββ
β=0,05
4,571
3,902
3,652
β
ββ
β=0,05
6,570
4,640
4,480
По результатам построения доверительных интервалов для среднего по k
этапам значения целевой функции z
ср
можно сделать следующий вывод; полу-
ширина доверительного интервала среднего значения целевой функции умень-
шается с ростом числа осредняемых этапов моделирования и уменьшением не-
определенности данных.
Аналогично построить для всех исходных переменных графики зависи-
мости погрешности оценивания параметра
δ
δδ
δ
( f ) от числа k этапов моделиро-
вания для всех уровней неопределенности исходных данных.
4) Для всех уровней неопределенности данных и числа этапов моделиро-
вания k = 100 построить таблицу относительных частот вхождения исходных
переменных в оптимальный план. Для рассматриваемой задачи таблица имеет
вид:
β
ββ
β
х
1
х
2
0.05
1,000 1,000
0.10
0,913 1,000
0.20
0,833 0,944
При
β
ββ
β
= 0,05 обе переменные входят в оптимальный план на всех этапах
имитационного эксперимента. С увеличением неопределенности данных отно-
сительная частота вхождения переменных в оптимальный план снижается.
5) Определить зависимость гарантированного уровня целевой функции z*
от риска операции R для трех уровней неопределенности данных. Рассмотреть
диапазон изменения риска операции R
∈
∈∈
∈
[0; 0.25]. Принять, что целевая функция
z
ср
распределена по нормальному закону
k
(z)
,MN~z
срср
σ
σσ
σ
, где М
ср
- среднее
Рис. 1.

57
арифметическое точечных оценок математического ожидания целевой функции
в 3-х имитационных экспериментах при k = 100,
σ
σσ
σ
( z ) – точечные оценки сред-
него квадратического отклонения, полученные в имитационном эксперименте
при k = 100. Функция z*( R ) в соответствии с введенным определением риска
операции для задачи минимизации вычисляется с помощью встроенной функ-
ции табличного процессора MS Excel:
z*( R ) = НОРМОБР
−
−−
−
k
(z)
,M,R1
ср
σ
σσ
σ
Результаты расчетов представить в таблице и в виде графика. Для рас-
сматриваемой модели имеет место:
640,3
3
009,4456,3403,3
М
ср
=
==
=
+
++
+
+
++
+
=
==
=
.
Тогда законы распределения целевой функции имеют вид:
z
∼
∼∼
∼
N(3.64; 0.0346) - для
β
ββ
β
= 0.05;
z
∼
∼∼
∼
N(3.64; 0.0882) - для
β
ββ
β
= 0.10;
z
∼
∼∼
∼
N(3,64; 0,1653) - для
β
ββ
β
= 0.20;
Таблица зависимости z*( R ) имеет вид:
Риск операции
β
ββ
β
0,01 0,05 0,10 0,15 0,20 0,25
0,05
3,543
3,519
3,506
3,497
3,490
3,484
0,10
3,665
3,605
3,573
3,551
3,534
3,519
0,20
3,881
3,757
3,692
3,647
3,612
3,582
Гарантированное значение целевой функции уменьшается с ростом риска
операции и уменьшением значения неопределенности данных.

58
Варианты.
0x
12xx2
4x
2xx
xxzmax.1
i
21
2
21
21
≥
≥≥
≥
≤
≤≤
≤+
++
+
≤
≤≤
≤
≤
≤≤
≤+
++
+
+
++
+=
==
=
0x
12xx2
4x
3xx5,0
xxzmax.2
i
21
2
21
21
≥
≥≥
≥
≤
≤≤
≤+
++
+
≤
≤≤
≤
≤
≤≤
≤+
++
+−
−−
−
+
++
+=
==
=
0x
5x
11x2x
10xx2
x2x3zmax.3
i
2
21
21
21
≥
≥≥
≥
≤
≤≤
≤
≤
≤≤
≤+
++
+
≤
≤≤
≤+
++
+
+
++
+=
==
=
0x
12xx2
4x
2xx
x2xzmax.4
i
21
2
21
21
≥
≥≥
≥
≤
≤≤
≤+
++
+
≤
≤≤
≤
≤
≤≤
≤+
++
+−
−−
−
+
++
+−
−−
−=
==
=
0x
12xx2
4x
3xx5,0
x3xzmax.5
i
21
2
21
21
≥
≥≥
≥
≤
≤≤
≤+
++
+
≤
≤≤
≤
≤
≤≤
≤+
++
+−
−−
−
+
++
+−
−−
−=
==
=
0x
5x
11x2x
10xx2
xxzmax.6
i
2
21
21
21
≥
≥≥
≥
≤
≤≤
≤
≤
≤≤
≤+
++
+
≤
≤≤
≤+
++
+
+
++
+−
−−
−=
==
=
0x
9xx
5x
4xx5,0
x3xzmax.7
i
21
2
21
21
≥
≥≥
≥
≤
≤≤
≤+
++
+
≤
≤≤
≤
≤
≤≤
≤+
++
+−
−−
−
+
++
+−
−−
−=
==
=
0x
9xx
5x
3xx
x2xzmax.8
i
21
2
21
21
≥
≥≥
≥
≤
≤≤
≤+
++
+
≤
≤≤
≤
≤
≤≤
≤+
++
+−
−−
−
+
++
+=
==
=
0x
8xx
4x
2xx
x2xzmax.9
i
21
2
21
21
≥
≥≥
≥
≤
≤≤
≤+
++
+
≤
≤≤
≤
≤
≤≤
≤+
++
+−
−−
−
+
++
+=
==
=
0x
6x
10x2x
3xx5,0
xxzmax.10
i
1
21
21
21
≥
≥≥
≥
≤
≤≤
≤
≤
≤≤
≤+
++
+
≤
≤≤
≤+
++
+−
−−
−
+
++
+=
==
=
0x
13xx2
2xx
5x
xxzmax.11
i
21
21
2
21
≥
≥≥
≥
≤
≤≤
≤+
++
+
≤
≤≤
≤−
−−
−
≤
≤≤
≤
+
++
+=
==
=
0x
5xx
14x2x
6x2x
x3xzmax.12
i
21
21
21
21
≥
≥≥
≥
≤
≤≤
≤−
−−
−
≤
≤≤
≤+
++
+
≤
≤≤
≤−
−−
−−
−−
−
+
++
+−
−−
−=
==
=
0x
5x
2xx
25x5x
x2x3zmax.13
i
1
21
21
21
≥
≥≥
≥
≤
≤≤
≤
≤
≤≤
≤−
−−
−
≤
≤≤
≤+
++
+
+
++
+=
==
=
0x
6xx2
14xx2
8x2x
x2x3zmax.14
i
21
21
21
21
≥
≥≥
≥
≤
≤≤
≤−
−−
−
≤
≤≤
≤+
++
+
≤
≤≤
≤+
++
+−
−−
−
+
++
+=
==
=

59
0x
4x3x2
4x
5x
x2xzmax.15
i
21
2
1
21
≥
≥≥
≥
≤
≤≤
≤−
−−
−
≤
≤≤
≤
≤
≤≤
≤
+
++
+−
−−
−=
==
=
0x
13xx2
5x
2xx
xxzmax.16
i
21
2
21
21
≥
≥≥
≥
≤
≤≤
≤+
++
+
≤
≤≤
≤
≤
≤≤
≤−
−−
−
+
++
+=
==
=
0x
4x
10xx2
6xx2
x3xzmax.17
i
2
21
21
21
≥
≥≥
≥
≤
≤≤
≤
≤
≤≤
≤+
++
+
≤
≤≤
≤−
−−
−
+
++
+−
−−
−=
==
=
0x
4x
8xx2
7xx
x2x3zmax.18
i
2
21
21
21
≥
≥≥
≥
≤
≤≤
≤
≤
≤≤
≤−
−−
−
≤
≤≤
≤+
++
+
+
++
+=
==
=
0x
7xx2
2x2x
3x
xxzmax.19
i
21
21
2
21
≥
≥≥
≥
≤
≤≤
≤−
−−
−
≤
≤≤
≤−
−−
−
≤
≤≤
≤
+
++
+=
==
=
0x
8xx2
4x3x2
18x3x
x3xzmax.20
i
21
21
21
21
≥
≥≥
≥
≤
≤≤
≤−
−−
−
≤
≤≤
≤−
−−
−
≤
≤≤
≤+
++
+
+
++
+−
−−
−=
==
=
0x
2x2x
7xx2
20x5x
xxzmax.21
i
21
21
21
21
≥
≥≥
≥
≤
≤≤
≤−
−−
−
≤
≤≤
≤−
−−
−
≤
≤≤
≤+
++
+
+
++
+−
−−
−=
==
=
0x
3xx
8xx2
4x
x2x3zmax.22
i
21
21
2
21
≥
≥≥
≥
≤
≤≤
≤−
−−
−
≤
≤≤
≤−
−−
−
≤
≤≤
≤
+
++
+−
−−
−=
==
=
0x
9xx2
2x3x
12x2x
xxzmax.23
i
21
21
21
21
≥
≥≥
≥
≤
≤≤
≤−
−−
−
≤
≤≤
≤−
−−
−
≤
≤≤
≤+
++
+
+
++
+−
−−
−=
==
=
0x
9x2x3
6x
12xx3
xx2zmax.24
i
21
2
21
21
≥
≥≥
≥
≤
≤≤
≤−
−−
−
≤
≤≤
≤
≤
≤≤
≤−
−−
−
+
++
+−
−−
−=
==
=
60
Лабораторная работа № 6
"Решение и моделирование задач транспортного типа"
Рассматривается транспортная задача с транзитом со стохастическими
исходными данными. Исследование ведется с помощью пакета программ
"Компьютерное моделирование".
При обработке данных имитационного эксперимента для транспортной
задачи с транзитом строятся доверительные интервалы для средних за n циклов
значения минимальн6ых транспортных расходов и потоков на элементах сети;
оцениваются вероятности попадания маршрута в оптимальный план; определя-
ется зависимость средних предельных транспортных расходов от величины до-
пускаемого риска; строится функция суммарных затрат на получение информа-
ции об исходных данных модели и гарантию предельного уровня транспортных
расходов от неопределенности данных.
