Трухний А.Д. Паротурбинная установка блоков Балаковской АЭС

Подождите немного. Документ загружается.

§ 2.5] ТРЕУГОЛЬНИКИ СКОРОСТЕЙ 49_

пара, выходящими из сопловой решетки, но

и реактивной силой ускоряющегося в рабочей

решетке пара.

Разделение ступеней на активные и реактивные

условно и справедливо только для ступеней с малой

веерностью т.е. для ступеней с короткими

по сравнению с диаметром решетки лопатками. При

параметры пара изменяются по высоте, и в

корневом сечении реактивность может быть близка

к нулю, а в периферийном может достигать 0,7

и выше. Таким образом, в общем случае правиль-

нее говорить не о реактивности ступени, а о реак-

тивности участка ступени, относящегося к какому-

либо радиусу.

Реактивность, по существу, определяется соотно-

шением площадей сечений для выхода пара в сопло-

вой и рабочей решетках. Если в условиях эксплуа-

тации оно изменяется (например, из-за поврежде-

ний выходных кромок рабочих лопаток, вызвавших

уменьшение площади сечения выхода), то это при-

ведет к изменению экономичности и надежности

(из-за роста осевого усилия на диск).

2.5. ТРЕУГОЛЬНИКИ СКОРОСТЕЙ

Наглядное представление о режиме работы сту-

пени и ее экономичности дают диаграммы векторов

скоростей потока пара, называемые треугольни-

ками скоростей.

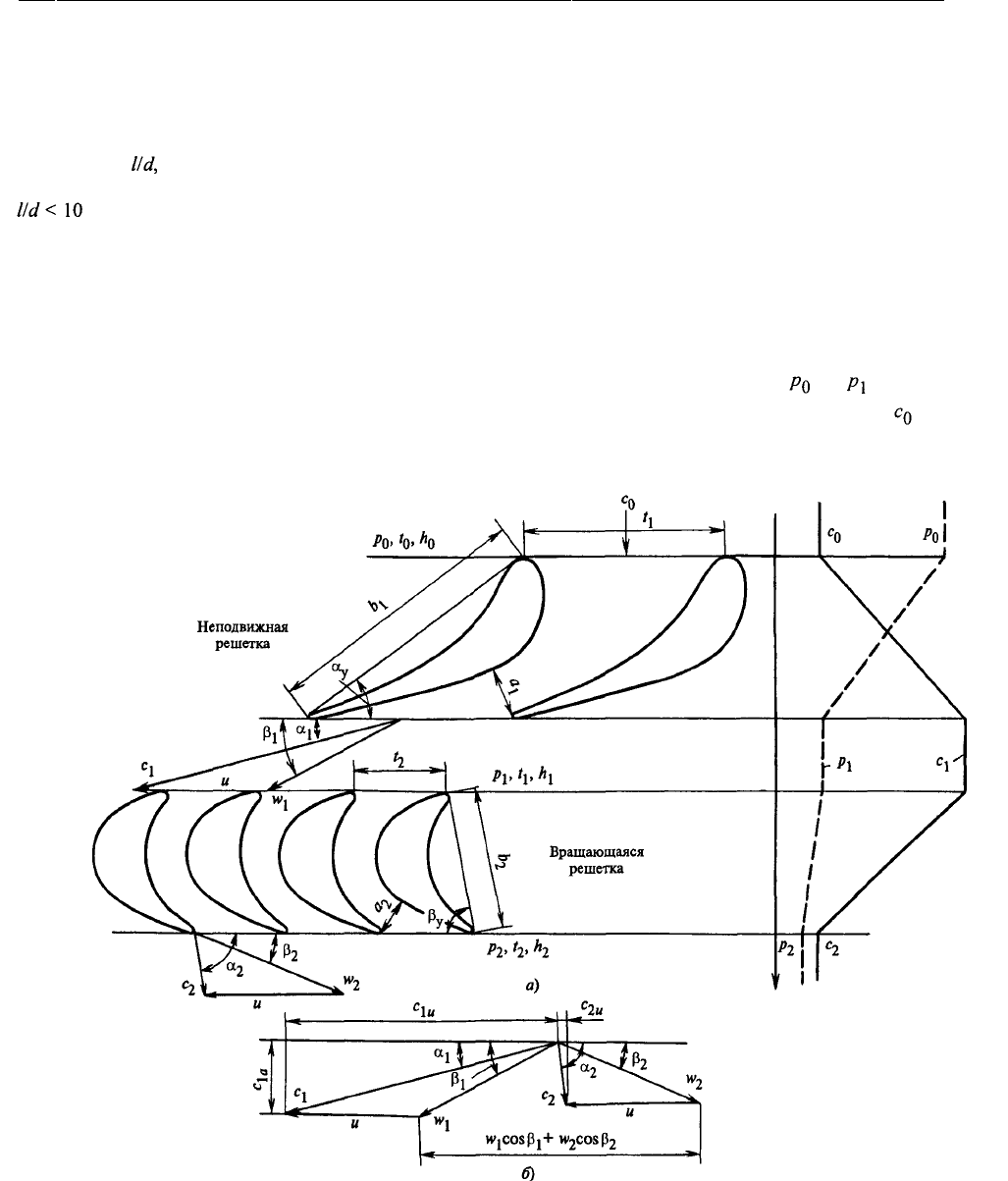
На рис. 2.11, а справа схематически показано,

как за счет расширения пара уменьшается его дав-

ление в сопловой решетке от до . При этом

если на входе в решетку скорость пара была

мала, то на выходе она существенно возрастает

Рис. 2.11. Треугольники скоростей для ступени:

а — векторы скоростей потока; б — треугольники скоростей

50 ТЕПЛОВОЙ ПРОЦЕСС В ПАРОВОЙ ТУРБИНЕ И ЕЕ ПРИНЦИПИАЛЬНОЕ УСТРОЙСТВО [Гл 2

до значения и направлена под углом опреде-

ляемым соотношением

(2.21)

Скорость выхода пара из сопловой решетки

наглядно изображается вектором Однако на

профили движущейся решетки пар будет поступать

не под углом а под другим углом, так как

решетка вращается с окружной скоростью, изобра-

жаемой вектором модуль которого равен

(2.22)

где — угловая скорость вращения; — диаметр

ступени. В результате пар натекает на рабочие

лопатки под углом с относительной скоростью

равной разности векторов и . Профили

рабочих лопаток должны быть выбраны и установ-

лены так, чтобы обеспечить безударный вход пара

на рабочую решетку. В этом случае в ней не будет

больших потерь.

Построенные таким образом векторы образуют

треугольник, часто называемый входным тре-

угольником скоростей (для рабочей решетки).

Пар, поступив в каналы рабочей решетки, взаи-

модействует с ее профилями, создавая окружную

силу вращающую диск. Покидает пар рабочую

решетку с относительной скоростью значение

которой подсчитывается по соотношению (2.17),

а угол выхода в относительном движении определя-

ется по формуле

(2.23)

где — ширина канала рабочей решетки на выходе.

Абсолютная скорость выхода пара представ-

ляет собой сумму векторов и Она будет

составлять угол с плоскостью вращения. Полу-

ченный треугольник векторов скоростей называют

выходным треугольником скоростей (для

рабочей решетки).

Входной и выходной треугольники скоростей

обычно совмещают (см. рис. 2.11, б) и кратко назы-

вают треугольниками скоростей. Они позволяют

лучше понять, каким образом в ступени внутренняя

энергия пара превращается в работу. Напомним,

что при протекании пара через сопловую решетку

техническая работа не производится, так как решет-

ка закреплена в неподвижной диафрагме, но зато

пар разгоняется от скорости до скорости В рабо-

чей решетке скорость потока уменьшается от значе-

ния до значения и именно поэтому на рабочих

лопатках возникает движущее окружное усилие и

совершается работа. Подсчитать возникающую

окружную силу можно с помощью известной

из школьного курса физики теоремы импульсов,

утверждающей, что изменение количества движе-

ния пара в окружном направлении за 1 с

равно импульсу окружной силы, т.е.

(2.24)

Из рис. 2.11, б следует, что чем меньше углы

и тем большая сила возникает на лопатках.

Однако большее значение вовсе не означает

большую эффективность преобразования внутрен-

ней энергии пара в работу.

Действительно, представим себе чисто актив-

ную ступень, в которой площадь выходного сече-

ния рабочих каналов постоянна. Тогда по уравне-

нию неразрывности (см. рис. 2.4, б)

и, следовательно, Пусть треуголь-

ники скоростей для такой ступени представлены

на рис. 2.12, а сплошными линиями. Если умень-

шить теплоперепад ступени, оставив неизменными

угол и окружную скорость (т.е. частоту враще-

ния), то треугольники скоростей изменятся (штри-

ховые линии). Нетрудно видеть, что при этом

окружное усилие уменьшится, но экономичность

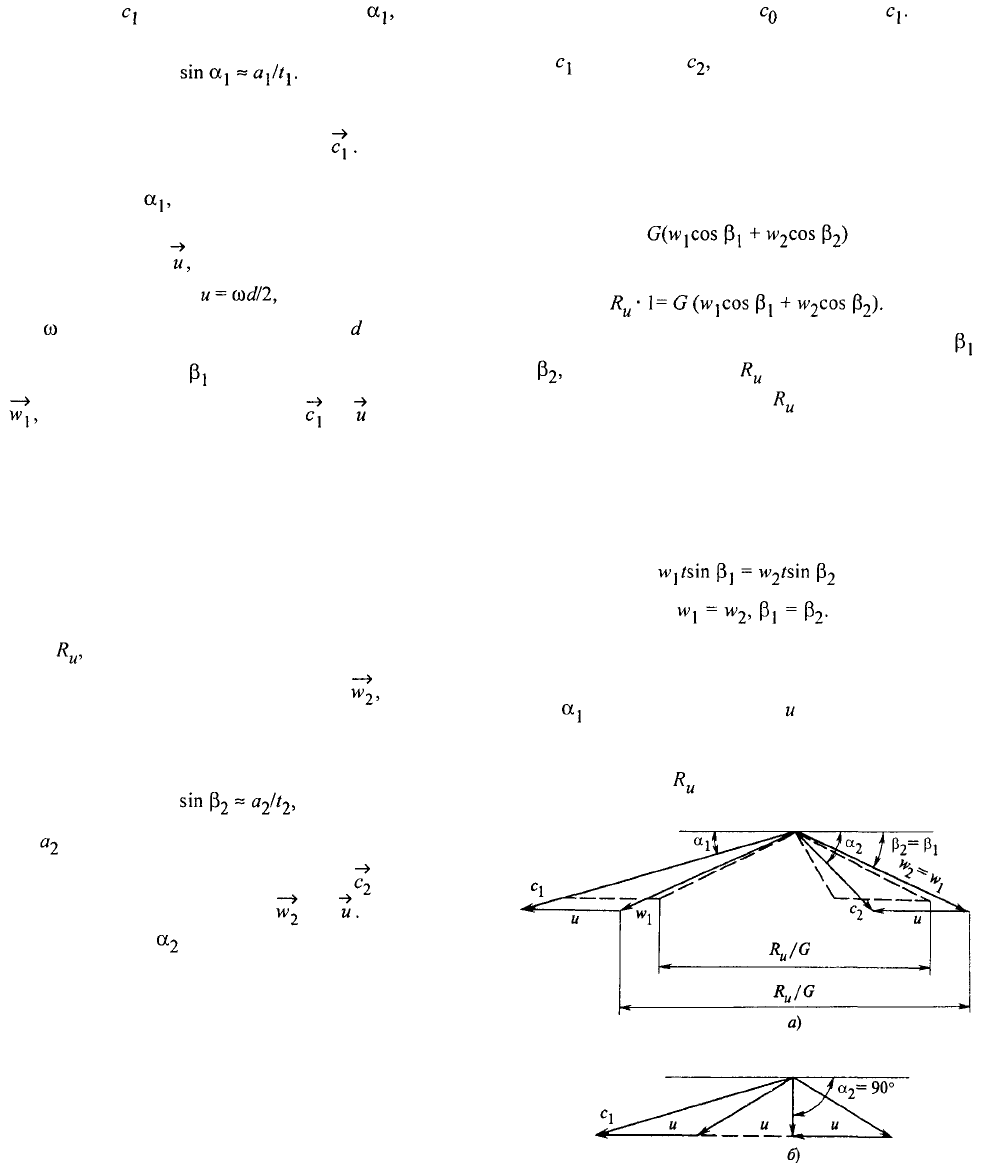
Рис. 2.12. Неоптимальные (а) и оптимальные (6)

треугольники скоростей

§ 2.5] ТРЕУГОЛЬНИКИ СКОРОСТЕЙ 51

ступени возрастет, так как уменьшится потеря с вы-

ходной скоростью из-за уменьшения скорости

При дальнейшем уменьшении теплоперепада

скорость будет продолжать уменьшаться и, нако-

нец, примет минимальное значение при

В этом случае треугольники скоростей будут опти-

мальными и приобретут вид, показанный на

рис. 2.12, б. Очевидно, в этом случае

Так как угол обычно мал то

для обеспечения максимальной экономичности на

номинальном режиме работы ступень должна

быть спроектирована так, чтобы окружная ско-

рость рабочих лопаток была примерно вдвое меньше

скорости выхода пара из сопл.

В практических расчетах удобнее в качестве

характеристики оптимальности ступени использо-

вать не отношение а близкое к нему отношение

где —фиктивная (условная) ско-

рость, определяемая из соотношения

(2.25)

Для реальных активных ступеней оптимальное

значение определяется соотношением

(2.26)

и лежит в пределах 0,42—0,55. Для реактивных сту-

пеней

Существование для ступени оптимального отно-

шения как мы увидим ниже, имеет глубокий

смысл и очень сильно влияет на конструкцию всей

турбины.

Пример 2.2. Определить основные размеры проточ-

ной части промежуточной ступени турбины, работающей

на влажном паре, и построить для нее треугольники ско-

ростей по следующим исходным данным: начальные пара-

метры

расход пара через ступень частота вращения

Условия задачи примерно соответствуют усло-

виям работы четвертой ступени турбины К-1000-5,9/25-2.

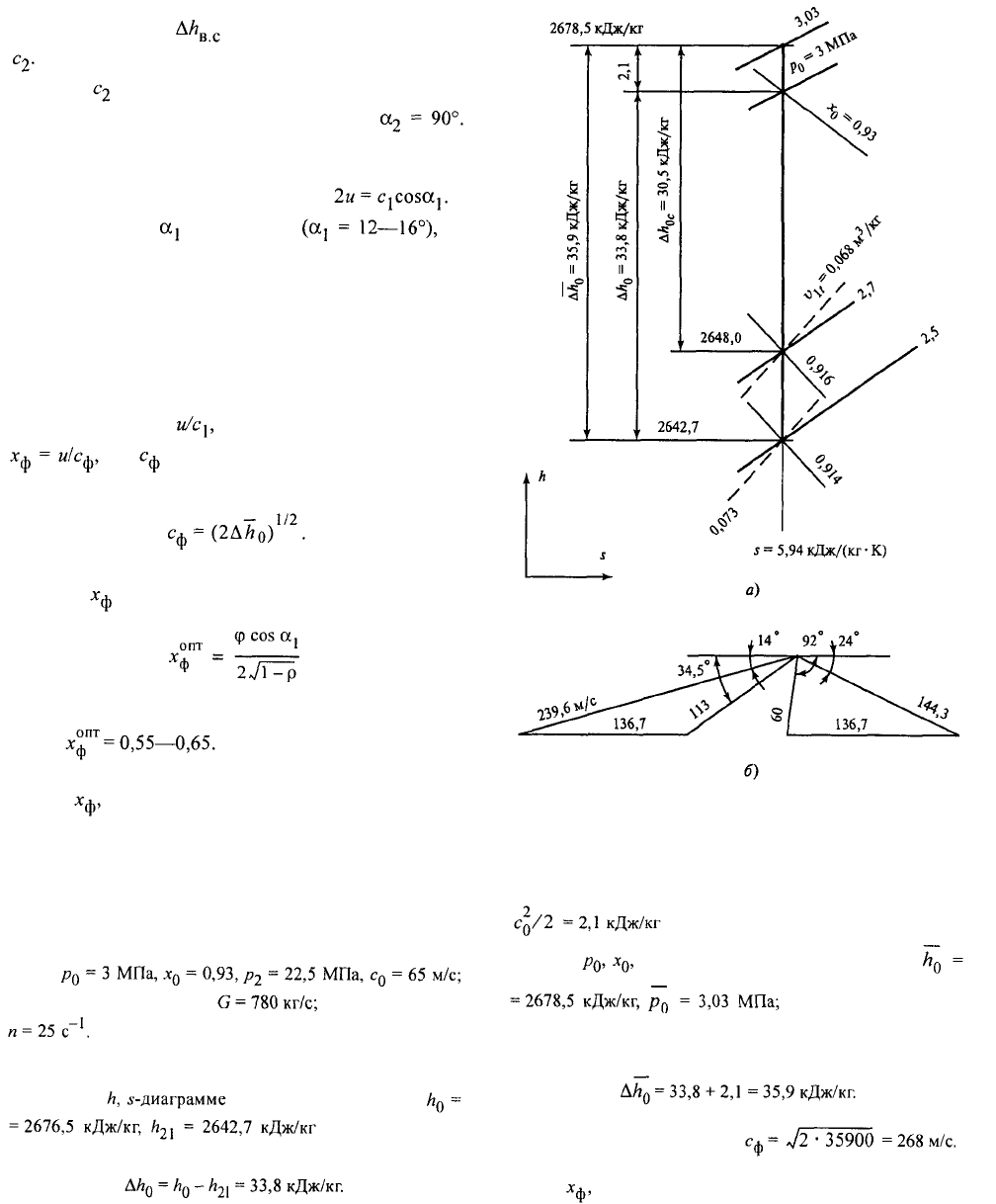
Строя изоэнтропный процесс расширения пара

в ступени в (рис. 2.13, а), получаем

и, следовательно,

располагаемый теплоперепад

Рис. 2.13. Процесс расширения пара (см. пример 2.2)

в ступени турбины (а) и треугольники скоростей для нее (б)

Определяя кинетическую энергию на входе в ступень

и откладывая ее вверх от точки с пара-

метрами получаем параметры торможения:

располагаемый тепло-

перепад ступени, подсчитанный по параметрам тормо-

жения,

Тогда фиктивная скорость

Определим из соотношения (2.26) оптимальное отно-

шение задавшись следующими значениями: реактив-

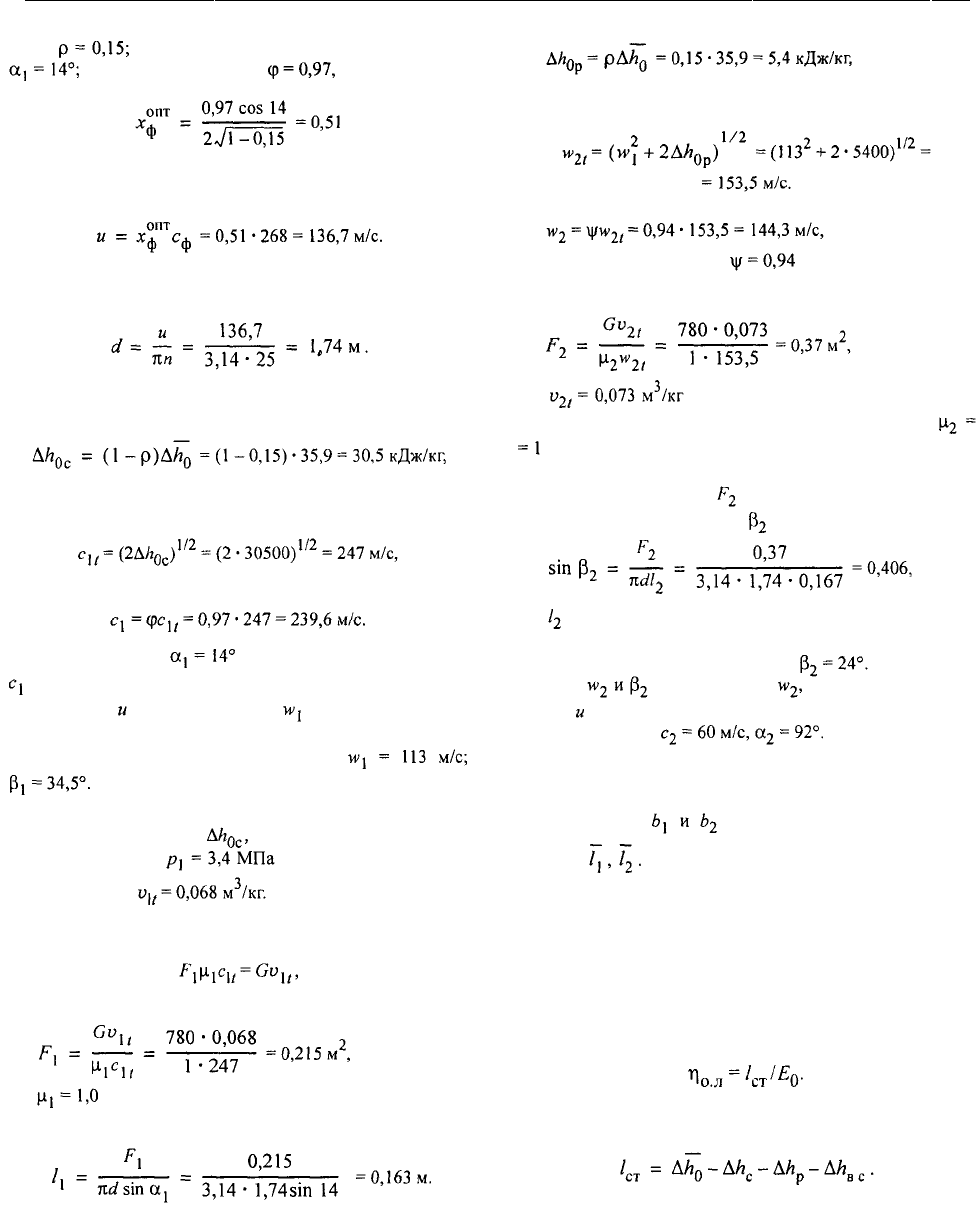
52 ТЕПЛОВОЙ ПРОЦЕСС В ПАРОВОЙ ТУРБИНЕ И ЕЕ ПРИНЦИПИАЛЬНОЕ УСТРОЙСТВО [Гл. 2

ность угол выхода потока из сопловой решетки

коэффициент скорости тогда

и, следовательно, окружная скорость вращающейся ре-

шетки для обеспечения максимального КПД должна быть

Поскольку частота вращения задана, диаметр ступени

должен быть равен

Построим входной треугольник скоростей. Распола-

гаемый теплоперепад сопловой решетки

и тогда теоретическая скорость выхода пара из сопловой

решетки

а фактическая

Строя под углом в некотором масштабе вектор

(см. рис 2.13, б), пристраиваем к нему вектор окруж-

ной скорости и получаем вектор скорости входа пара

на рабочие лопатки в относительном движении. Путем

непосредственного измерения получаем

Откладывая от параметров торможения вниз по изо-

энтропе теплоперепад определяем давление за

сопловой решеткой и теоретический удель-

ный объем пара

Используя уравнение неразрывности для выходного

сечения сопловой решетки

определяем площадь этого сечения:

где — принятый по оценке коэффициент расхода.

Тогда высота сопловой решетки

Перейдем к построению выходного треугольника.

Теплоперепад рабочей решетки

и, следовательно, теоретическая скорость пара на выходе

из нее в относительном движении

Действительная скорость

где коэффициент скорости принят по оценке.

Площадь выходного сечения рабочей решетки полу-

чается из уравнения неразрывности:

где — удельный объем пара за рабочей

решеткой при изоэнтропном процессе расширения;

— принятый коэффициент расхода для рабочей

решетки.

Выходная площадь обеспечивается при вполне

определенном значении угла , для которого

где — высота рабочей решетки, принятая для безудар-

ного входа потока на 4 мм больше высоты сопловой

решетки. Таким образом, получаем

Зная ,строим вектор пристраиваем к нему

вектор и получаем (см. рис. 2.13, б) выходной треуголь-

ник, для которого

Принятые по оценке коэффициенты скорости φ и ψ

могут быть уточнены с помощью соотношений (2.12)

и (2.16) после выбора из условия прочности размеров

хорд профилей и определения относительных

величин

2.6. ОТНОСИТЕЛЬНЫЙ ЛОПАТОЧНЫЙ

КПД ТУРБИННОЙ СТУПЕНИ

Относительный лопаточный КПД представляет

собой отношение полезной работы, развиваемой

ступенью, к располагаемой энергии ступени:

(2.27)

Полезная работа ступени (см. рис. 2.9) определя-

ется соотношением

(2.28)

Располагаемая энергия — это энергия, которая

может быть преобразована в данной ступени в ра-

боту. Если ступень расположена так, что ее выход-

§ 2.7) ОТНОСИТЕЛЬНЫЙ ВНУТРЕННИЙ КПД СТУПЕНИ 53

некоторое оптимальное соотношение скоростей

при котором КПД максимален. Поскольку

окружная скорость и ограничена прочностью вра-

щающихся деталей (дисков, лопаток), ограничен-

ной оказывается и скорость т.е. теплоперепад

срабатываемый в одной ступени.

Именно поэтому турбина выполняется многосту-

пенчатой.

Пример 2.3. Определить относительный лопаточный

КПД ступени, рассмотренной в примере 2.2.

Так как рассматриваемая ступень промежуточная и

выходная скорость может быть использована в после-

дующей ступени, то

Потери энергии в решетках

Потеря с выходной скоростью

Полезная работа ступени определяется по формуле

(2.28):

Следовательно,

2.7. ОТНОСИТЕЛЬНЫЙ ВНУТРЕННИЙ

КПД СТУПЕНИ

Кроме потерь в решетках и с выходной скоро-

стью в ступени имеются дополнительные потери:

с утечками пара, на трение дисков о пар, от наличия

капель влаги.

Потери с утечками связаны с тем, что часть

пара протекает через зазоры ступени и полезной

работы не совершает.

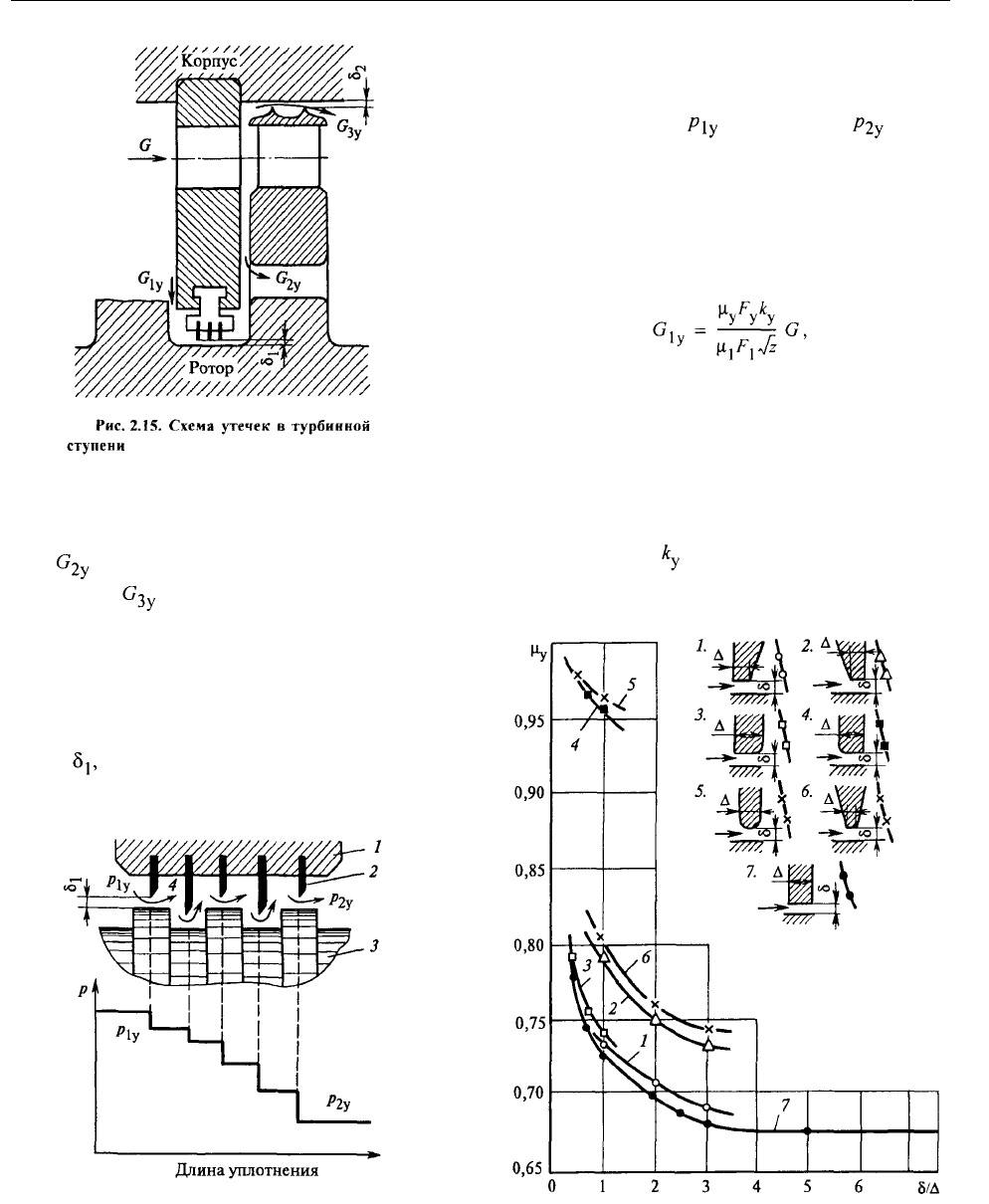
Это относится к пару (рис. 2.15), протекаю-

щему через диафрагменное уплотнение и посту-

пающему либо через так называемые разгрузочные

отверстия в диске (для разгрузки упорного подшип-

ника от осевого усилия) к диафрагме следующей

ступени, либо в корневое сечение рабочей лопатки.

Поэтому в корневом сечении ступени выполня-

ют с такой реактивностью и разгрузочные отвер-

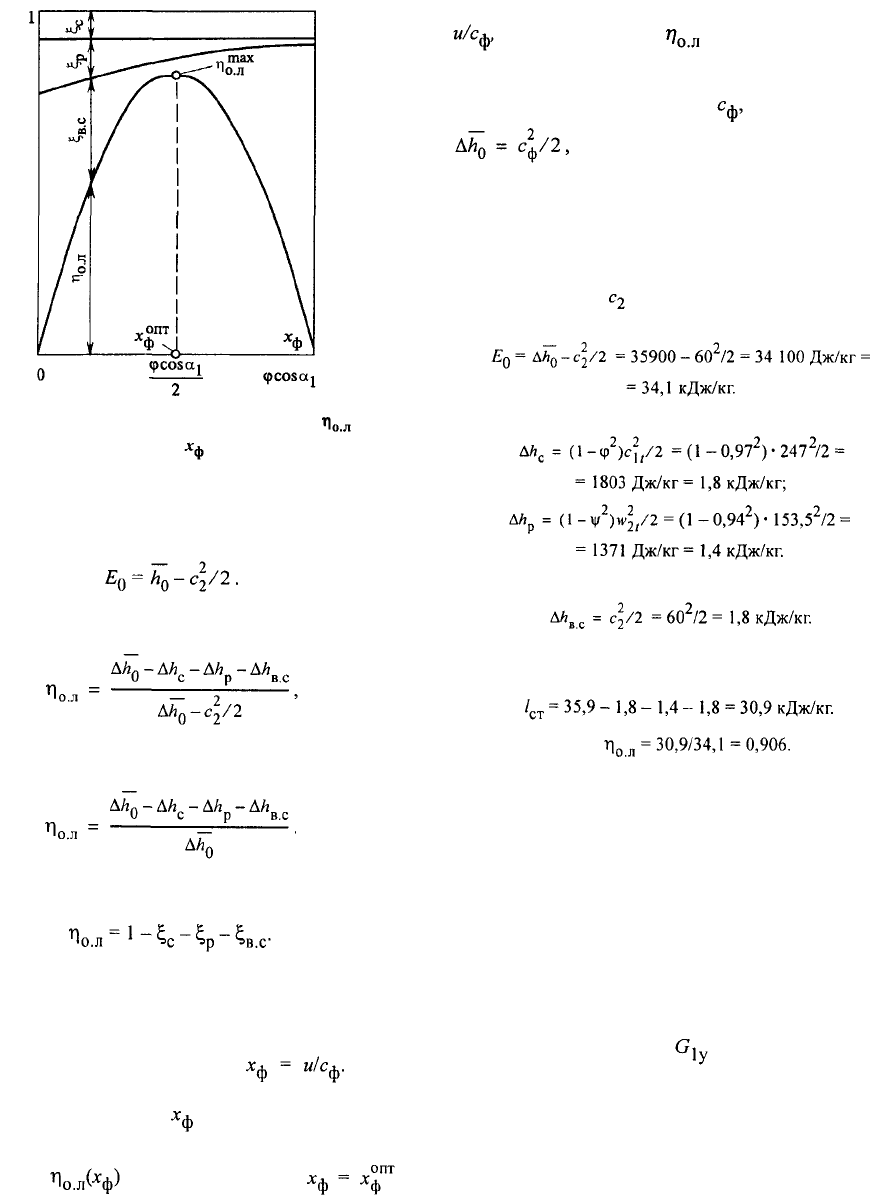
Рис. 2.14. Зависимость потерь и КПД

от отношения скоростей при постоянных φ

и ψ для чисто активной ступени

ная скорость не может быть использована (напри-

мер, в последней ступени), то

Таким образом, для ступени, за которой исполь-

зуется выходная скорость,

(2.29)

а для ступени, за которой выходная скорость не ис-

пользуется,

(2.30)

Если использовать относительные потери в сту-

пени, то

(2.31)

Таким образом, относительный лопаточный

КПД учитывает качество решеток ступени и по-

терю с выходной скоростью.

Наибольшее влияние на относительный лопаточ-

ный КПД оказывает отношение Если

потери в сопловой и рабочей решетках сравни-

тельно слабо зависят от (рис. 2.14), то потери

с выходной скоростью определяют параболический

вид кривой с максимумом при

(см. соотношение (2.26)). Таким образом, имеется

54 ТЕПЛОВОЙ ПРОЦЕСС В ПАРОВОЙ ТУРБИНЕ И ЕЕ ПРИНЦИПИАЛЬНОЕ УСТРОЙСТВО [Гл. 2

стия делают такого размера, которые исключили бы

подсос пара в проточную часть из зазора между

диафрагмой и диском. Но в этом случае возникает

утечка в обвод рабочей решетки.

Часть пара проходит над бандажом рабочих

лопаток, также не совершая работы.

Для уменьшения утечек между вращающимися

и неподвижными элементами устанавливают

лабиринтное уплотнение, схема которого

показана на рис. 2.16. Уплотнение создается тонки-

ми кольцевыми гребнями, установленными с малым

зазором и камерами, расположенными между

гребнями. Пар, проходя между гребнем и валом,

приобретает кинетическую энергию, которая затем

гасится в расширительной камере. В результате

по мере движения пара через уплотнение его давле-

ние уменьшается от перед ним до за ним.

Расход пара через уплотнение определяется давле-

нием перед последним гребнем, которое тем меньше,

чем больше гидравлическое сопротивление предше-

ствующих гребней.

Утечка пара через диафрагменное уплотнение

определяется соотношением

(2.32)

где G — расход пара через ступень; z — число греб-

ней; μ

и F

— соответственно коэффициент расхода

и площадь выходного сечения сопловой решетки;

Fу — площадь сечения для прохода пара под

последним гребнем; μ

— коэффициент расхода

(рис. 2.17), зависящий от формы и размеров гребня

и зазора под ним; — поправочный коэффициент,

зависящий от конструкции уплотнения.

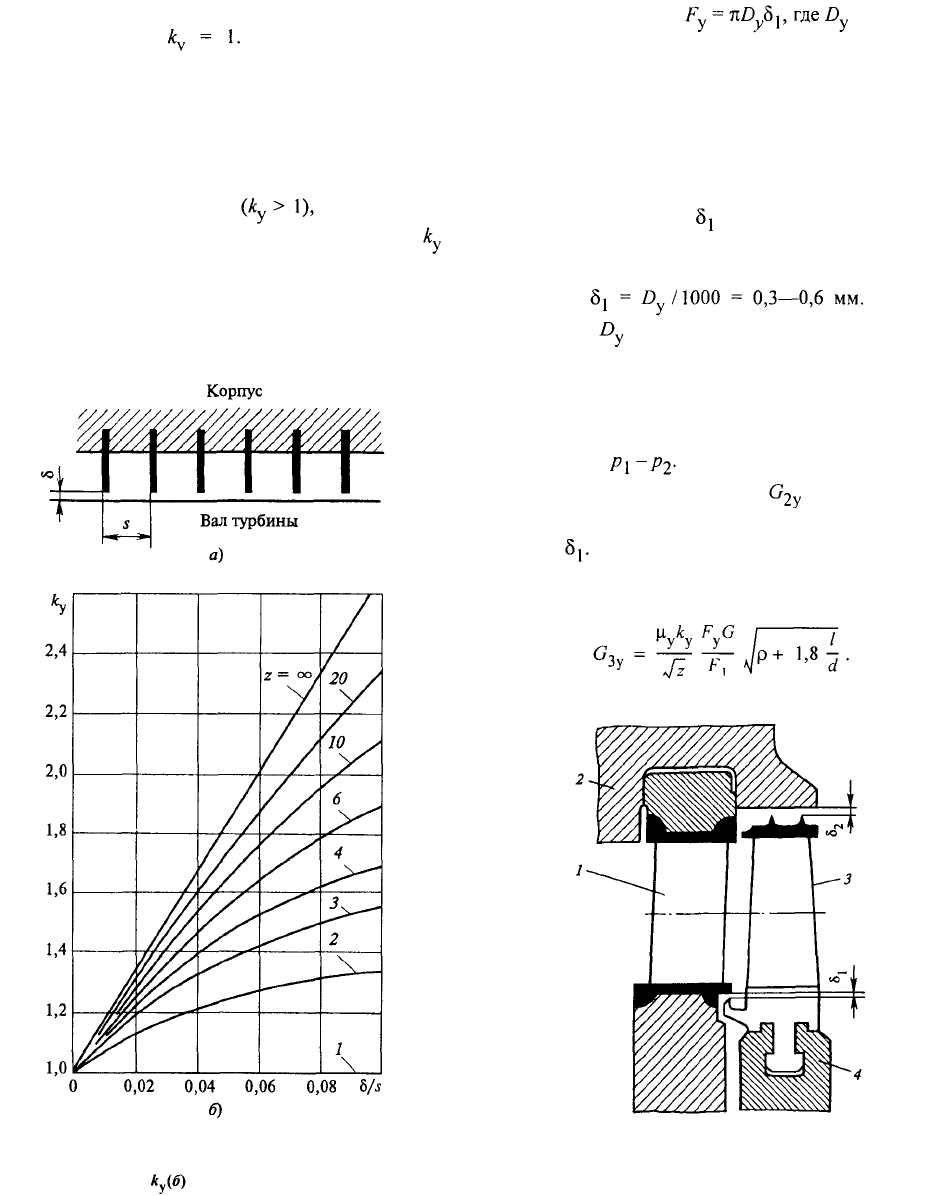
Рис. 2.16. Лабиринтное уплотнение:

/ — сегмент уплотнения; 2 — гребни; 3 — участок вала; 4 —

расширительная камера

Рис. 2.17. Коэффициент расхода μ

для зазоров с греб-

нями различной формы

§ 2.7] ОТНОСИТЕЛЬНЫЙ ВНУТРЕННИЙ КПД СТУПЕНИ 55

Для ступенчатого уплотнения (см.

рис. 2.16), в камерах которого происходит полное

гашение скорости, Однако ступенчатые

уплотнения не могут применяться там, где в про-

цессе эксплуатации могут быть большие относи-

тельные смещения ротора и статора и могут возни-

кать осевые задевания ротора о статор. Тогда

используют прямоточные уплотнения (рис. 2.18, а),

в камерах которых не происходит полного гашения

скорости и протечка больше чем в ступен-

чатых уплотнениях. Графики для определения

приведены на рис. 2.18, б.

Из соотношения (2.32) видно, что утечка через

диафрагменное уплотнение обратно пропорцио-

нальна корню квадратному из числа уплотняющих

гребней и прямо пропорциональна площади сече-

ния для прохода пара — диаметр

уплотнения.

Поэтому если в результате небрежной эксплуа-

тации, в частности при проведении пусков с боль-

шой вибрацией, происходят износ уплотнений

[изменение формы гребней (см. рис. 2.17)] и увели-

чение зазоров, то это приводит к росту утечек

и снижению экономичности.

Уменьшение зазора в уплотнении ограничива-

ется возможностью задеваний ротора о статор

и возникновения тяжелой аварии. Как правило,

выбирают Диаметр

уплотнения также стараются уменьшить, однако

его минимальное значение ограничивается вибра-

ционными характеристиками валопровода. Умень-

шение диаметра вала также приводит к возраста-

нию осевой силы, действующей на диск из-за разно-

сти давлений

Для уменьшения утечки (см. рис. 2.15)

выполняют корневое уплотнение (рис. 2.19) с малым

зазором

Утечка пара поверх бандажа определяется соот-

ношением

(2.33)

Рис. 2.19. Схема уплотнения ступени:

/ — сопловая решетка; 2 — корпус турбины; 3 — рабочая

лопатка; 4 — диск

Рис. 2.18. Схема прямоточного уплотнения

(а) и график для определения поправочного

коэффициента

56 ТЕПЛОВОЙ ПРОЦЕСС В ПАРОВОЙ ТУРБИНЕ И ЕЕ ПРИНЦИПИАЛЬНОЕ УСТРОЙСТВО [Гл. 2

После вычисления суммарной утечки , не уча-

ствующей в производстве работы, потеря от утечки

определится соотношением

(2.34)

а относительная потеря от утечек

(2.35)

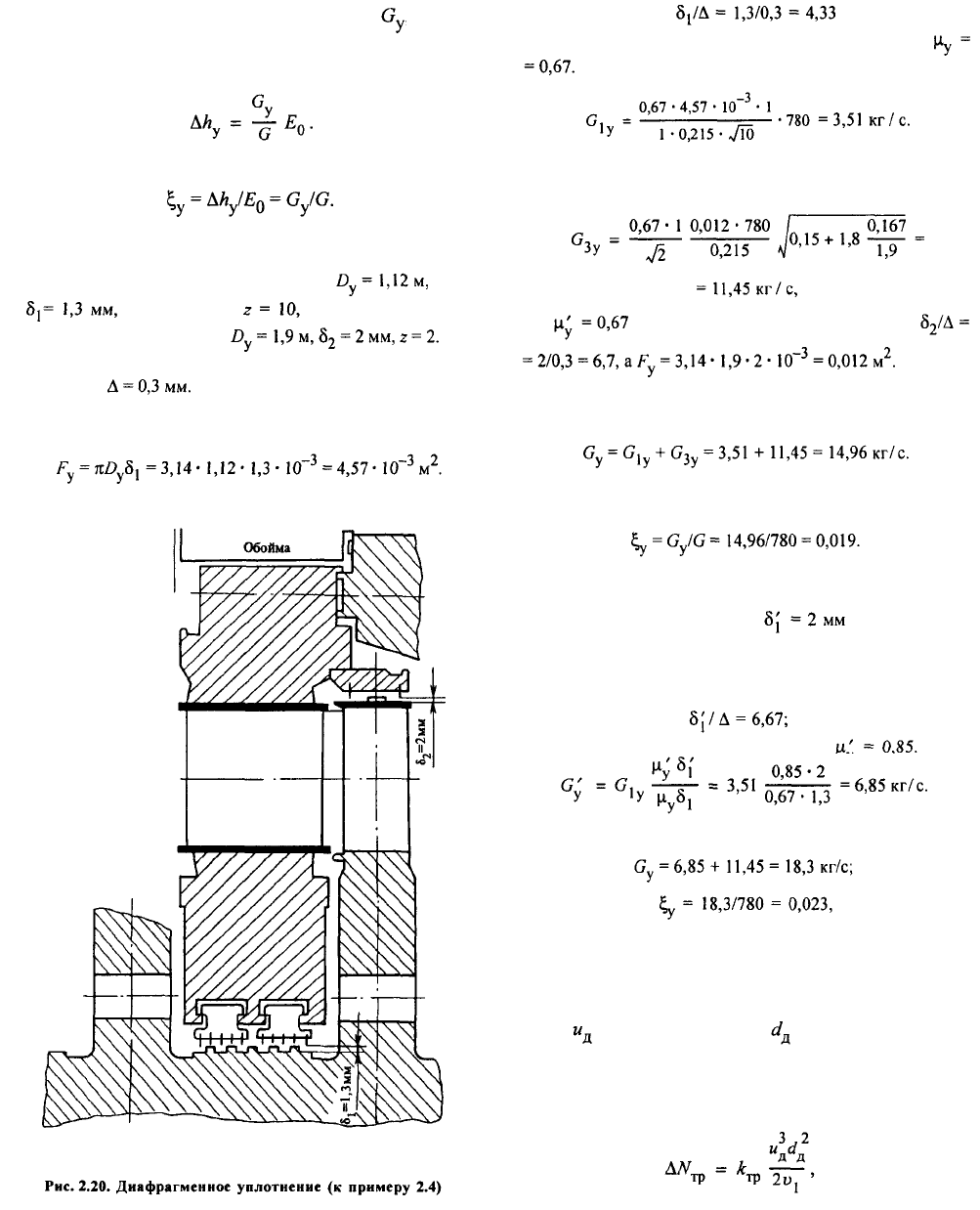
Пример 2.4. Определить потери от утечек для ступе-

ни, рассмотренной в примере 2.2, если средний диаметр

диафрагменного уплотнения (рис. 2.20) зазор

число гребней а для надбандажного

уплотнения (см. рис. 2.19)

Исходная форма — гребень с острыми кромками и

толщиной

Площадь зазора для прохода пара в диафрагменном

уплотнении

По отношению с помощью кри-

вой 7 на рис. 2.17 находим коэффициент расхода

Из соотношения (2.32) имеем

Утечка через надбандажное уплотнение определяется

по соотношению (2.33):

где найдено, как и ранее, по отношению

Суммарная утечка

Относительная потеря от утечек

Пример 2.5. Определить изменение потери от утечки

при разработке диафрагменного уплотнения, рассмотрен-

ного в примере 2.4, до зазора при изменении

формы гребней до полукруглой (см. поз. 5 на рис. 2.17).

Утечка через уплотнение изменится пропорционально

изменению зазора и коэффициенту расхода. Для изно-

шенного уплотнения из рис. 2.17 (неуверен-

ная экстраполяция кривой 5) получим Тогда

утечка через разработанное уплотнение

Суммарная утечка

потеря от утечек т.е. увеличилась

почти на 70 %.

Потери на трение в ступени вызываются

силами трения между вращающимся диском и

паром. Они тем выше, чем больше окружная ско-

рость диска, его диаметр и плотность среды,

в которой вращается диск. Мощность, кВт, затрачи-

ваемая на преодоление сил трения, определяется

по формуле:

(2.36)

§ 2 7) ОТНОСИТЕЛЬНЫЙ ВНУТРЕННИЙ КПД СТУПЕНИ 57_

где — окружная скорость, м/с;

— диаметр диска, м; — удельный объем,

Потери на трение определяются по формуле

(2.37)

а относительные потери на трение

(2.38)

Если из работы лопаток ступени вычесть потери

от утечек и трения, то получится внутренняя работа

ступени, развиваемая на валу турбины:

Отношение внутренней работы ступени к ее рас-

полагаемой энергии называется относительным

внутренним КПД ступени:

(2.39)

Таким образом,

Пример 2.6. Определить относительный внутренний

КПД ступени, рассмотренной в примерах 2.2—2.5.

Диаметр диска

Окружная скорость на периферии диска

Принимая и полагая

подсчитываем по формуле (2.36) мощность, затрачивае-

мую на преодоление сил трения:

Потери от трения

Следовательно,

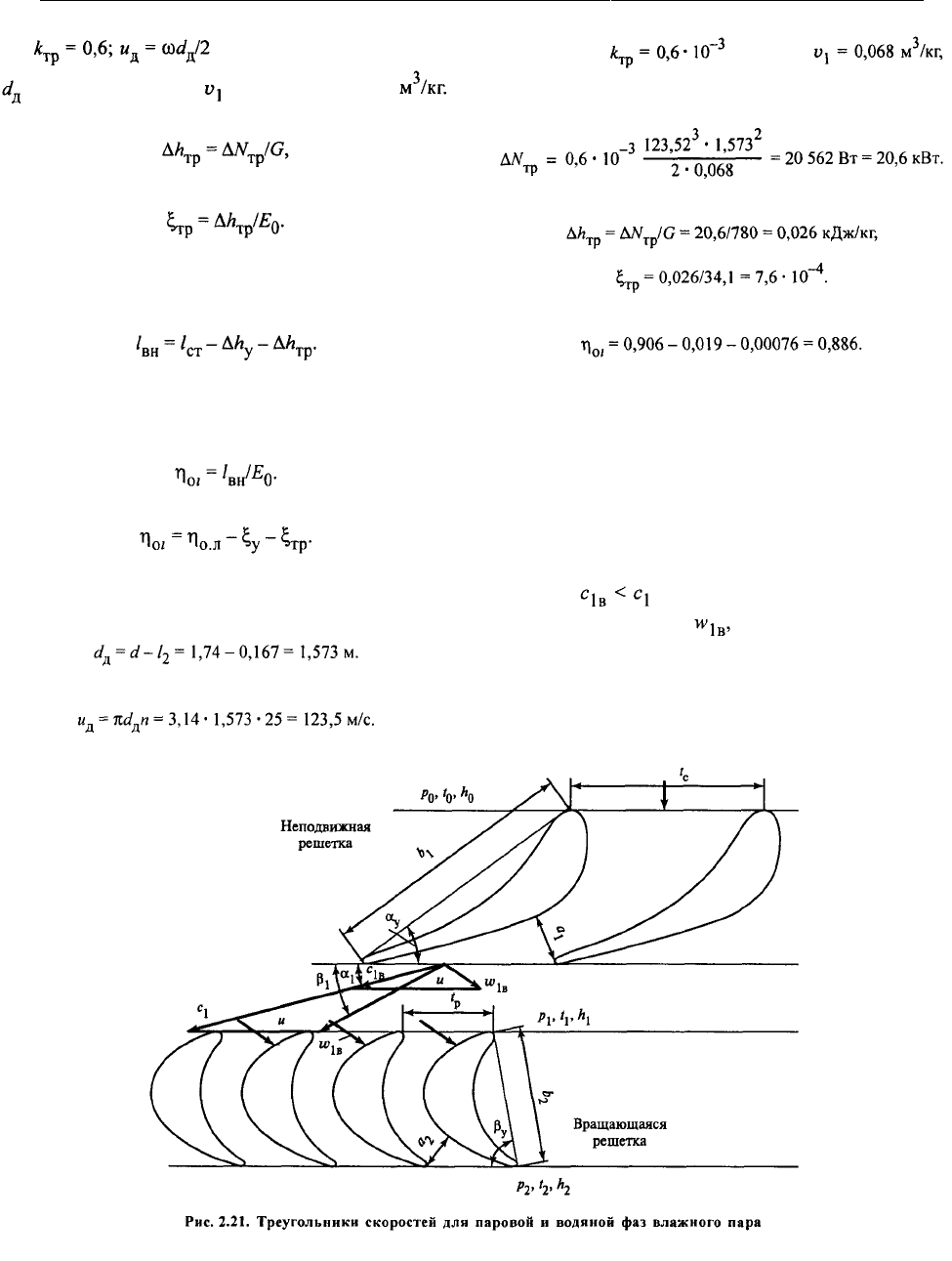
В последних ступенях турбин протекает влаж-

ный пар, что приводит к потерям от влажно-

сти и дополнительному снижению относительного

внутреннего КПД. Капли влаги, особенно крупные,

движутся по своим траекториям, отличным от тра-

екторий течения пара. В частности, они вызывают

тормозящий эффект, понятный из рис. 2.21. Капли

влаги, проходя через сопловую решетку, не успе-

вают разогнаться до скорости пара, приобретают

скорость и в результате входят в рабочую

решетку со скоростью направленной навстречу

окружной скорости движения диска и.

Имеющиеся исследования влияния влажности

на относительный внутренний КПД показывают,

что каждый дополнительный процент влажности

58 ТЕПЛОВОЙ ПРОЦЕСС В ПАРОВОЙ ТУРБИНЕ И ЕЕ ПРИНЦИПИАЛЬНОЕ УСТРОЙСТВО [Гл. 2

снижает на 0,5—1 %, и в первом приближении

его можно определить по соотношению

(2.40)

где — средняя влажность в ступени; — КПД

с учетом влажности;

2.8. СТУПЕНИ С ЗАКРУЧЕННЫМИ

ЛОПАТКАМИ

При выходе из сопловой решетки (см. рис. 2.11, б)

вектор скорости имеет осевую и окружную

составляющие, которые заставляют частицы

пара двигаться по винтовым траекториям; причем

на каждую частицу пара действует центробежная

сила, стремящаяся отбросить ее к периферии.

Но поскольку здесь расположена ограничивающая

стенка (корпус турбины), то в результате по радиу-

су в зазоре между сопловой и рабочей решетками

устанавливается распределение давления, уравно-

вешивающее центробежную силу частиц пара. Дав-

ление пара в зазоре увеличивается от корневого

сечения к периферийному.

Наоборот, как видно из рис. 2.11, б, окружная

составляющая скорости на выходе из правильно

спроектированной ступени мала, и поэтому давле-

ние практически постоянно по высоте. Постоян-

ным будет и давление на входе в ступень.

Таким образом, при практически неизменных

по высоте давлениях и и, следовательно, рас-

полагаемых теплоперепадах на различных радиусах

из-за переменности давления в зазоре реактив-

ность будет возрастать от корневого сечения

к периферийному.

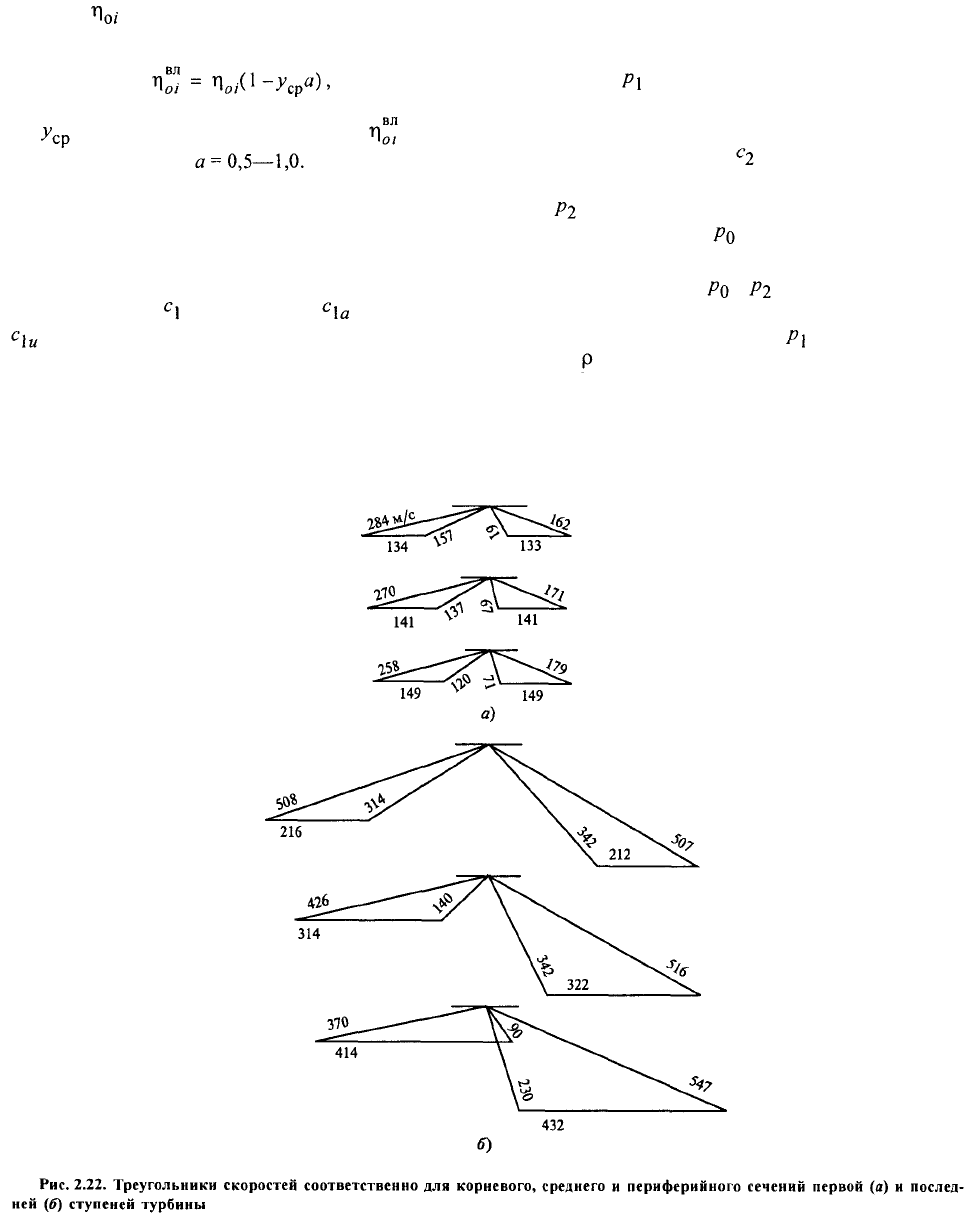
Изменение реактивности и окружной скорости

по высоте ступени приводит к существенному

изменению треугольников скоростей (рис. 2.22),