Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны

Подождите немного. Документ загружается.

241

окрестности ε, вне которой скорость Ψ(x) сразу после удара равна 0.

Поэтому условие (10.23) можно записать в виде:

ξ+ε

ξ−ε

Ψ(x) dx =

(ε > 0) (10.24)

и Ψ(x) = 0 при x /∈ [ξ − ε, ξ + ε].

При неограниченном уменьшении длины отре зка, по которому ударяет

моло точек, на нем функция Ψ(x) неограниченно растет, но все время

выполняется условие (10.23).

Итак, функция Φ(x) = 0, а функция Ψ(x) всюду равна нулю, за исклю-

чением исчезающе малой окрестности точки x = ξ и для нее имеет место

условие (10.23). С учетом сказанного вычислим по формулам (10.22) ам-

плитуды A

и B

. Очевидно, что B

= 0, а

πmv

ξ+ε

ξ−ε

Ψ(x) sin

πm

xdx ≈

πmρv

sin

πm

ξ , (10.25)

где формула тем точнее, чем меньше ε.

Задача 10.1. Задача. Считая, что Ψ(x) = p/ρδ(x −ξ), где δ — обобщенная

δ — функция (δ — функция Дирака), найдите решение задачи о струне

рояля.

Из соотношения (10.25) следует, что максимальная ам плитуда колеба-

ний не основной частоте πv/l и на частотах гармоник 2πv/l, 3πv/l . . . рав-

ны, соответственно, 2p/(πρv) sin(πξ/l), p/(πρv) sin(2πξ/l),

2p/(3πρv) sin(3πξ/l) . . . . Распределения стоячих волн вдоль струны для

основного тона n = 1 и первых трех гармоник n = 2, n = 3 и n = 4 пред-

ставлены на рис. 10.5. Как из него следует, основной тон преобладает при

ударе по центру струны, но при этом не возбуждаются вторая и четвертая

гармоники. Для т ого, чтобы эффективно возбудились несколько первых

гармоник, следует ударить недалеко от концов струны. Более того, чем

меньше удаление от точки закрепления 1 струны, тем больше гармоник

возбудится. Именно так делается в рояле, и именно этим различаются

разные инструменты. Процитируем по этому поводу книгу [1]. “У Стен-

вея это расстояние меньше, чем у Бехштейна, и поэтому его “звонче”, но

зато звук Бехштейна “бархатнее” и “мягче”. Звук скрипичной струны и

фортепианной одного и того же основного тона сильно различаются и это

отличие также объясняется различностью представительности гармоник.

242

n=1

n=2

n=3

x=0

x=l

n=4

(x)

Рис. 10.5. Распределение вдоль струны стоячих волн на

частоте основного тона n = 1 и на частотах первых трех

гармоник n = 2, n = 3, n = 4.

Наше ухо устроено так, что звук воспринимает его как спектр. Му-

зыкальные звуки до, ре, ми, . . . имеют спектр, состоящий из основного

тона и гармоник. Музыкальные аккорды имеют спектр, составленный из

спектров, входящих в него музыкальных звуков . . .

Почему опреде ленные последовательности звуков вызывают у нас та-

кие сильные эмоции, пожалуй, одна из величайших загадок природы. Хо-

тя некоторые необходимые для этого требования известны и состовляют

предмет теории музыки”.

§ 3. Волны в одномерном резонаторе.

Резонанс в олновых систем

В главе 9 мы обсуждали неко торые свойства общего линейного урав-

нения в частных производных L[ϕ] = 0, где L — линейный дифференци-

альный оператор с постоянными коэффициентами. Конкретизитуем вид L,

сохранив, однако, определенную общность.

Пусть уравнение, описывающее распространение волн в среде, можно

записать следующим образом:

∂u

∂t

+ B

∂u

∂x

+ Cu = 0 , (10.26)

где A, B и C — матрицы, а u — вектор. Будем искать решение (10.26) в

виде

u = Ψe

i(ωt−kx

, (10.27)

243

Ψ(Ψ

, Ψ

, . . . , Ψ

) — комплексный вектор (поляризационный вектор), ком-

поненты которого Ψ

есть коэффициенты распределения, характеризую-

щие соотношение амплитуд различных физических переменных в гармо-

нической волне.

Подставляя (10.27) в (10.26) приходим к алгебраической системе урав-

нений для Ψ

. Условие существования нетривиального решения этой си-

стемы и будет искомым дисперсионным уравнением

det(Aω − Bk − iC) = D(ω, k) = 0 . (10.28)

Пусть уравнение (10.28) имеет решения ω = ω

(k) и k = k

(w) где s =

= 1, 2, . . . , n. Это означает, что в среде существует n типов волн, т. е.

u(x, t) =

s=1

i[ω

t−k

(ω)x]

+ k.c. ;

к. с. означает комплексно-сопряженную величину. Как и в случае со-

средоточенных систем (см. главы 3 и 7), можно перейти к нормальным

волнам:

(x, t) = Ψ

i(ω

t−k

Ввиду отсутствия связи между нормальными волнами они удовлетворяют

уравнениям

∂a

∂x

+ ik

= 0 , s = 1, 2, . . . , n . (10.29)

Такая запись удобна и т огда, когда между волнами появляется слабая

связь: в уравнение (10.29) в этом случае необходимо добавить слагае-

мое а, с соответствующим коэффициентом связи (связанным волнам мы

посвятим далее отдельную главу).

Мы уже указывали, что для распределенных систем дисперсионное

уравнение — это уравнение, связывающее две комплексные величины ω

и k. Для сосредоточенных же систем имеется характеристическое урав-

нение, которое дает более полную информацию о системе — спектр ее

комплексных собственных частот.

Есть ли аналог подобного уравнения для распределенной системы?

На примере струны уже можно положительно ответить на этот вопрос.

Попробуем получить ответ в более общем случае, для чего обратимся

к системам, в которых предполагается наличие обратной связи (будем

называть их резонаторами). В простейшем случае такая обратная связь

244

осуществляется в кольцевом резонаторе. В кольцевом резонаторе может

реализоваться как режим чисто бегущей волны, так и режим суперпози-

ции встречных волн, частным случаем которого является стоячая волна

Для установления в кольце стоячей волны необходимо подобрать началь-

ные условия. В более общем случае обратная связь, превращающая вол-

новод в резонатор, обязана своим происхождением различного рода неод-

нородностям — стенкам, зерка лам, на которых бегущая волна достаточно

сильно или полностью отражается, передавая энергию встречной волне.

Примером могут служить оптический резонатор Фабри — Перо и линия

передачи, закороченная или разомкнутая на концах. Решение при этом

представляется в виде суперпозиции встречных волн:

u(x, t) = Ψ

i(ωt−kx)

+ Ψ

i(ωt+kx)

, (10.30)

амплитуды которых в простейшем случае идеального отражения концах

резонатора должны равняться друг другу по модулю. Например, в слу-

чае рассмотренной выше струны, закрепленной на концах, u(0, t) = 0 и

u(l, t) = 0 (l — длина струны). Из (10.30) получаем условие для ампли-

туд встречных волн Ψ

= −Ψ

и ограничение на спектр волновых чисел

sin kl = 0, откуда

= πn/l , (n — целое) . (10.31)

Нетрудно проверить, что в любом одномерном резонаторе с предельным

отражением на концах могут реализоваться лишь элементарные решения,

удовлетворяющие (10.31), т. е. в резонаторе укладывается целое число по-

луволн. В кольцевом резонаторе граничными условиями служат условия

периодичности для всех переменных. Например, для замкнутой в коль-

цо линии передачи это U , I(x, t) = U , I(x + l, t), откуда следует условие

exp(ikl) = 1, т. е. спектр

= 2πn/l . (10.32)

Физически это условие совершенно очевидно — в кольцевом резонаторе

могут существовать лишь периодические в пространстве волны, кото-

рые укладываются в нем целое число раз. Зная дисперсионное уравнение

среды, заполняющей резонатор: D = (ω, k) = 0, и спектр волновых чи-

сел (10.31) или (10.32), мы можем получить уравнение относительно од-

ной переменной: ∆(ω) = D(ω, k

) = 0, определяющее спектр нормальных

частот резонатора. Именно это уравнение и есть аналог характеристиче-

ского уравнения для сосредоточенных систем. Например, в случае среды

245

3 4

k k

ω ω ω ω

1 2 3 4

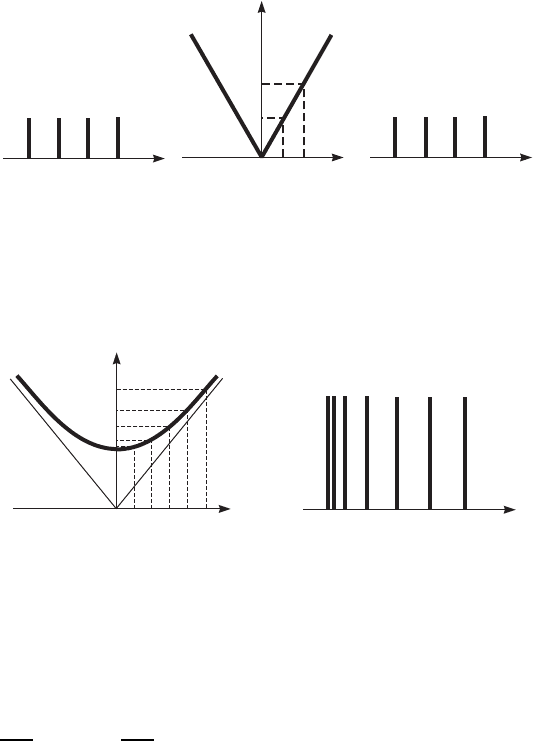
Рис. 10.6. Эк видистантный спектр собственных частот, со-

ответствующий эквидистантному спектру волновых чисел,

в среде без дисперсии.

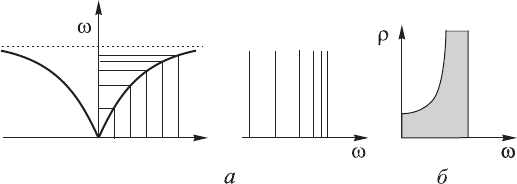
Рис. 10.7. Неэквидистантный спектр собственных частот,

соответствующий эквидистантному спектру волновых чи-

сел, в среде с дисперсией в области низких частот.

без дисперсии при идеальных отражениях на концах k

= πn/l и w

= πn/(l

√

LC) = k

√

LC рис. 10.6. Каким при эквидистантном спектре k

будет спектр ω, если среда обладает дисперсией? Качественное поведение

спектра, зная дисперсионные характеристики, можно получить с помо-

щью элементарного графического построения, которое ясно из рис. 10.7

и 10.8.

В среде с дисперсией в области низких частот спектр собственных

частот начинается с частоты ω

(рис. 10.8,), сгущается вблизи этой кри-

тической частоты; далеко от ω

спектр почти эквидистантный. При стрем-

лении ω к ω

спектр становится непрерывный. В среде с дисперсией в

области высоких частот картина такая же, но спектр становится редким

при приближении к нулевой частоте (рис. 10.8,a). Если имеются две кри-

тические частоты, то имеются и две области сгущения спектра.

246

Рис. 10.8. Неэквидистантный спектр собственных частот,

соответствующий эквидистантному спектру волновых чи-

сел, в среде с дисперсией в области высоких частот (а) и

плотность числа осцилляторов для низкочастотной ветви

(б)

Заметим, что когда речь идет о нахождении собственных частот длин-

ных линий, представленных эквивалентными схемами, с произвольными

граничными условиями на концах, то спектр волнового числа k

находит-

ся из известного характеристического уравнения tg kl = iY (Z

+ Z

)/(1 +

), где Y — характеристическая проводимость длинной линии, Z

и Z

— нагрузки при x = 0 и x = l соответственно [3, 4]. Кроме рассмо-

тренных случаев отметим еще один: линия коро ткозамкнута на одном и

разомкнута на д ругом конце, т. е. Z

= 0, Z

= ∞ (или Z

= ∞, Z

= 0),

тогда k

= π(2n − 1)/(2l).

Таким образом, если среда, заполняющая резонатор, обладает диспер-

сией, то даже при эквидистантном спектре k плотность ρ(ω) нормальных

мод в различных участках спектра будет различной. Это дает один из

способов измерения дисперсионных свойств одномерных сред, о собенно

ценный, например, при исследовании цепочек л инейных полимеров. До-

пустим, м ы смогли равномерно возбудить все степени свободы цепочки,

тогда снятый экспериментально спектр ее колебаний будет просто су-

перпозицией плотностей спектральных распределений, соответствующих

различным дисперсионным ветвям. Для каждой ветви плотность спек-

трального распределения (плотность числа осцилляторов) вводится фор-

мулой

ρ(ω)dω = const · dk . (10.33)

Здесь учтено, чт о ч исло мод в интервале (k,k + dk) для одномерной це-

почки не зависит от k. Для продольных колебаний цепочки из тожде-

ственных молекул с точностью до нормирующего множителя из (10.33)

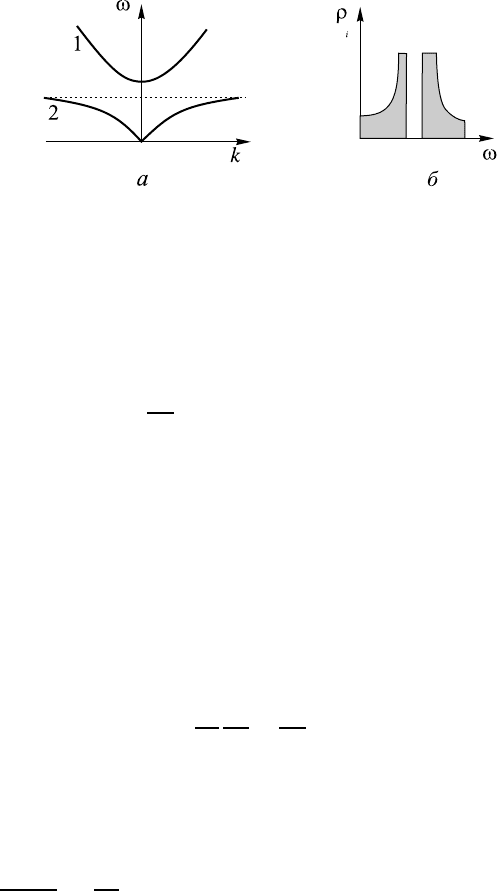
247

Рис. 10.9. Дисперсия (а) и плотность спектрального рас-

пределения (б) в среде с двумя ветвями дисперсионной

характеристики: 1 — оптическая ветвь; 2 — акустическая

ветвь

мы имеем

ρ(ω) = const·(

dω

)

−1

= (2C/a)(ω

max

− ω

)

−1/2

. (10.34)

Этот спектр представлен на рис. 10.8. Аналогично нетрудно построить

плотность спектрального распределения ρ

(ω) цепочки из чередующихся

легких и тяжелых молекул (см. главу 8). Если возбуждены и продольные,

и поперечные колебания цепочки, то к спектру ρ

(ω) (см. (10.34)) следует

добавить спектр поперечных колебаний, определяемый из дисперсионного

уравнения ω(k) = B sin

(ka/2). Плотность спектрального распреде ления

частот полного спектра приведена на рис. 10.9 [5].

Упомянем о прямой пространственно — временной аналогии. Рассмо-

трим распространение бегущей волны

∂u

∂t

∂u

∂x

= 0

в одномерной среде (v

— постоянная фазовая скорость волны в сре-

де), на которую воздействует внешняя распределенная сила G(x, t) =

= G(x) exp(iωt). Тогда очевидно, что

∂u(x)

∂x

+ i

u(x) = G(x) если u(x, t) = u(x) exp(iωt) .

Это уравнение удобно переписать в интегральной форме (при условии

u(0) = 0):

u(x) = e

−iωx/v

G(ζ) e

iωζ/v

dζ , (10.35)

248

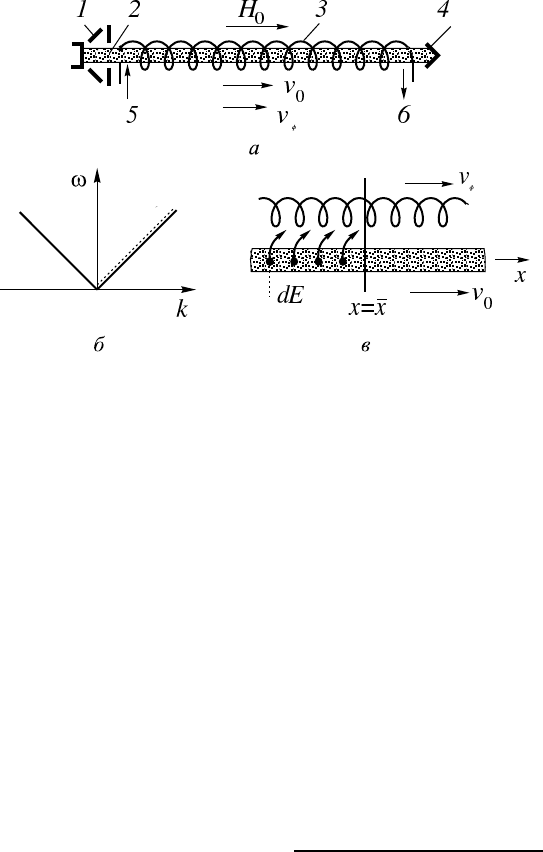
Рис. 10.10. Схема лампы бегущей волны: 1 — электронная

пушка; 2— электронный пучок; 3 — спираль; 4 — коллек-

тор; 5 и 6 — входное и выходное устройства; H

— ф окуси-

рующее магнитное поле (а); дисперсионные характеристи-

ки волны (сплошная линия) и пучка (штриховая линия)

для модели v

≈ v

(б) и иллюстрация пространственного

резонанса (в сечении x = ¯x поле есть суперпозиция полей,

создаваемых кажды элементом возмущенного пучка, рас-

положенным при x < ¯x; поля складываются в фазе, если

≈ v

(б).

где ζ — текущая переменная интегрирования.

Полагая, что G(x, t) = G(0) exp [i(ωt − ωx/v

вн

)], т. е. внешнее возму-

щение — волна постоянной амплитуды с частотой ω, бегущая с фазовой

скоростью v

вн

, и интегрируя (10.35), находим

u(x, t) = G(0) exp[i(ωt − ωx/v

)]

exp[i(ω/v

− ω/v

вн

)x] − 1

i(ω/v

− ω/v

вн

)

При ω/v

≈ ω/v

вн

получаем секулярный рост u(x, t) вдоль координаты x:

u(x, t) = G(0) x e

i(ωt−ωx/v

)

В этом, в частности, и проявляется пространственно-временная анало-

гия — для нарастания гармонической волны в пространстве под действи-

ем внешнего поля необходимо совпадение их пространственных периодов,

249

т. е. резонанс волновых чисел. В действительности здесь есть резонанс

и частот, и волновых чисел, что выражается в равенстве ф азовой ско-

рости собственной волны в среде фазовой скорости внешней волны. Это

условие обычно называют условием синхронизма волн. Если v

и v

вн

различаются сильно, то в системе возникнут пространственные биения

(длину волны биений легко определить). В случае, когда в среде может

распространяться много волн, т. е.

u(x, t) =

n=1

(n)

i(ω

t−k

и внешнее воздействие тоже многоволновое, условий синхронизма будет

n, т. е. будет n равенств фазовой скорости собственной волны на часто-

те ω

фазовой скорости внешней волны на той же частоте. Осознание

сформулированных нами условий синхронизма позволило в свое время

создавать электронные СВЧ — приборы с длительным взаимодействием

электронов и волны (наиболее известный из них — лампа с бегущей

волной — ЛБВ [6]). Для этих приборов время пролета электронов через

пространство взаимодействия много больше периода высокочастотных ко-

лебаний поля в отличие от резонансных СВЧ — приборов типа клистронов

приборов с кратковременным взаимодействием, о которых мы писали в

гл. 5.

Если считать, что u(x, t) — продольная составляющая электрического

поля E волны в волноведущей системе, a G(x, t) — волна переменно-

го тока I в электронном пучке (с точностью до размерного постоянно-

го коэффициента), то уравнение для u(x, t) есть уравнение возбуждения

волновода заданным током [7,8]:

∂E

∂x

+ i

E = −





KI(x) ,

где K имеет размерность сопротивления и называется сопротивлением

связи. Если прямолинейный электронный пучок с малой плотностью то-

ка представить как поток невзаимодействующих частиц, движущихся со

скоростью v

, то высокочастотные возмущения имеют вид волны тока

I(x, t) = I(0) exp[i(ωt −ωx/v

)] с фазовой скоростью v

вн

= v

). Таким

образом, простейшее условие синхронизма — это равенство конвектив-

ной скорости электронов фазовой скорости волны. Кстати, из этого усло-

вия следует необходимость при нерелятивистских скоростях электронов

замедлять электромагнитную волну (в большинстве ЛБВ используются

250

спиральные замедляющие системы; рис. 10.10). В случае, когда куло-

новы силы в пучке существенны, возмущения в нем распространяются

в виде волн пространственного заряда, скорости которых не равны v

Для пространственного резонанса в этом случае необходимо, чтобы был

синхронизм между одной из волн пространственного заряда и волной в

замедляющей системе. Следует заметить, что в своих рассуждениях мы

рассматривали лишь влияние внешней волны на собственную. В боль-

шинстве случаев это не так: при условии синхронизма есть и обратное

влияние. В ЛБВ, например, поле волноведущей системы модулирует пу-

чок по скорости и группирует электроны в сгустки, Такое взаимодействие

имеет место в случае связанных волн, которые мы рассмотрим в главе. 16.