Трубецков Д.И., Рожнев А.Г. Линейные колебания и волны

Подождите немного. Документ загружается.

201

Рис. 8.13. Цепочка из чередующихся осцилляторов двух

типов.

ную систему, предположив, что в цепочке последовательно чередуются

осцилляторы двух типов, назовем их A и B, отличающиеся массами и

собственными частотами колебаний ω

и ω

. Такая система показана

на рис. 8.13. Примем, вслед за Л.И. Манде льштамом [1, лекция 30], сле-

дующий способ обозначений: все осцилляторы в цепочке пронумеруем

подряд от 0 до 2N + 1, независимо от их типа, но координаты осцил-

лятора типа A будет обозначать через X

, типа B — через Y

. Тогда k

принимает нечетные значения k = 1, 3, . . . , 2N +1, а n — четные значения

n = 0, 2, . . . , 2N. Дл я определенности будет считать, что крайние осцил-

ляторы закреплены, тогда можно написать (сразу используем уравнения

для комплексных амплитуд)

= 0 , (8.82a)

2N+1

= 0 . (8.82b)

Для остальных осцилляторов записываем уравнения динамики в виде



−ω

+ ω



k+1

+ Y

k−1

) , k = 1, 3, . . . , 2N − 1 ,

(8.83a)



−ω

+ ω



n+1

+ X

n−1

) , n = 2, 4, . . . , 2N . (8.83b)

Решение уравнений (8.82) - (8.83) ищем в виде X

= A sin ψk, Y

= B sin ψn,

тогда уравнение (8.82a) выполняется автоматически, а подстановка этих

выражений в уравнения (8.83) после простых преобразований дает

(−ω

+ n

) A −

cos ψ B = 0 ,

−

cos ψ A + (−ω

+ n

)B = 0 ,

(8.84)

202

где n

= ω

+ 2k/M , n

= ω

+ 2k/m. Из (8.84) следует характеристи-

ческое уравнение

− (n

+ n

) + n

−

cos

ψ = 0 ,

Его решения есть

1,2

(ψ) =

+ n

) ∓

− n

)

cos

. (8.85)

Возможные значения ψ задаются, к ак и в случае однородной цепочки,

оставшимся уравнением (8.82b): sin ψ(2N + 1) = 0, или

πj

2N + 1

, j = 1, 2, . . . , N . (8.86)

Мы видим, что для к аждого возможного значения ψ из (8.86) можно

найти две собственные частоты, так что их общее число равно 2N, по

числу степеней свободы. Другие значения j, отличающиеся от 1, 2, . . . , N,

не приводят к новым решениям. Например, для j = N +1 можно записать

N+1

2N + 1

(N + 1) = π − ψ

Отсюда видно, что собственные частоты, получаемые для j = N и j =

= N + 1 из уравнения (8.85), совпадают, а распределения амплитуд ко-

лебаний осцилляторов X

, Y

отличаются только знаком. То же самое

можно сказать о собственных коле ба ниях с j = N −1 и j = N + 2, и так

далее.

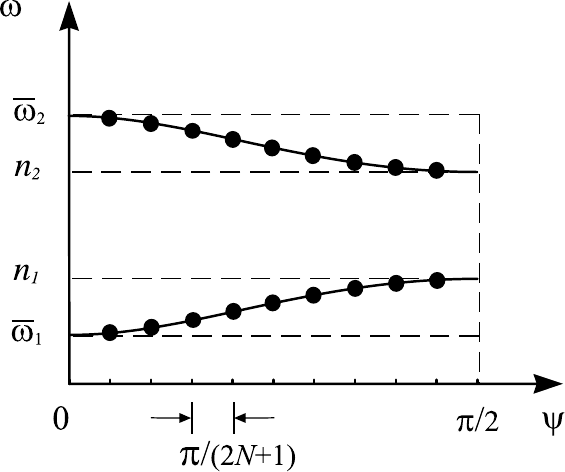
Если графически представить распределение собственных чисел, по-

добно тому, как это было сделано на рис. 8.10, то получится картина,

показанная на рис. 8.14. Собственные частоты, помеченные точками, ле-

жат на двух кривых, задаваемых уравнением (8.85). Координаты т очек

вдоль оси ψ определяются соотношением (8.86), из которого следует, что

возможный интервал изменения ψ ограничен значениями 0 и π/2. Каж-

дая ветвь спектра лежит в своей частотной полосе, нижняя ограничена

значениями ¯ω

и n

, а верхняя — значениями n

и ¯ω

, где

¯ω

1,2

+ n

) ∓

− n

)

. (8.87)

203

Рис. 8.14. Спектр колебаний цепочки из чередующихся ос-

цилляторов двух типов.

204

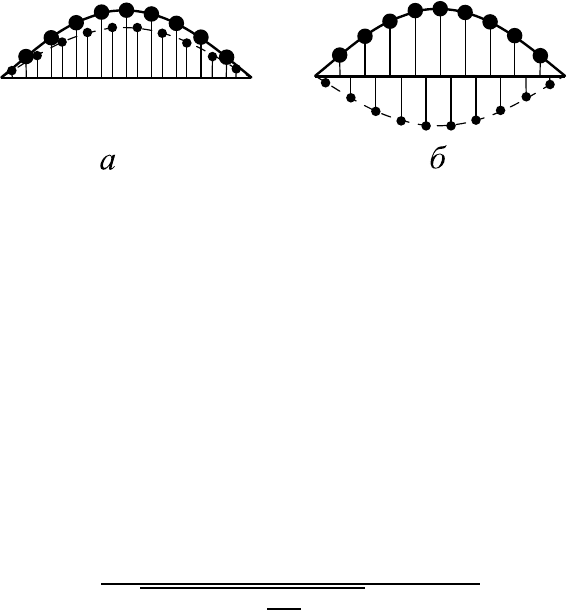
Рис. 8.15. Распределение амплитуд коле ба ний вдоль цепоч-

ки из чередующихся осцилляторов двух типов для первых

мод низкочастотной (а) и высокочастотной (б) ветвей спек-

тра.

Таким образом собственные частоты разбиты на две группы, лежащие,

соответственно, в первой и второй полосе. Собственные моды, принад-

лежащие первой группе называют низкочастотными, а второй группе —

высокочастотными. Они отличаются также пространственным распреде-

лением амплитуд колебаний. Из первого уравнения в (8.84) можно полу-

чить

A =

(4k/m) cos ψ

− n

)

cos

ψ − (n

− n

)

B ,

где знак плюс относится к низкочастотным, а минус — к высокочастот-

ным колебаниям. В первом случае амплитуды A и B имеют одинаковые

знаки, т. е. смещения соседних осцилляторов разного типа происходят в

фазе, а во втором A и B имеют разные знаки, т. е. смещения соседних

осцилляторов происходят в противофазе. Для основного типа колебаний

картины распределения амплитуд схематически показаны на рис. 8.15.

Случай (а) соответствует низкочастотной моде, при этом оба сорта осцил-

ляторов смещаются в одном направлении и макроскопическая плотность

заметно меняется в процессе колебаний. В случае (б), соответствующем

высокочастотным колебаниям, смещения происходят в разные стороны, и

заметного изменения плотности среды нет.

Если цепочку рассматривать как одномерную модель кристалла или

полимерной молекулы, то осцилляторы представляют атомы двух сор-

тов, расположенных в пределах одного периода кристаллической решетки.

При этом следует также учесть, что один отдельный атом вне кристал-

ла при смещении не испытывает возвращающей силы. Тогда ω

= 0 и

205

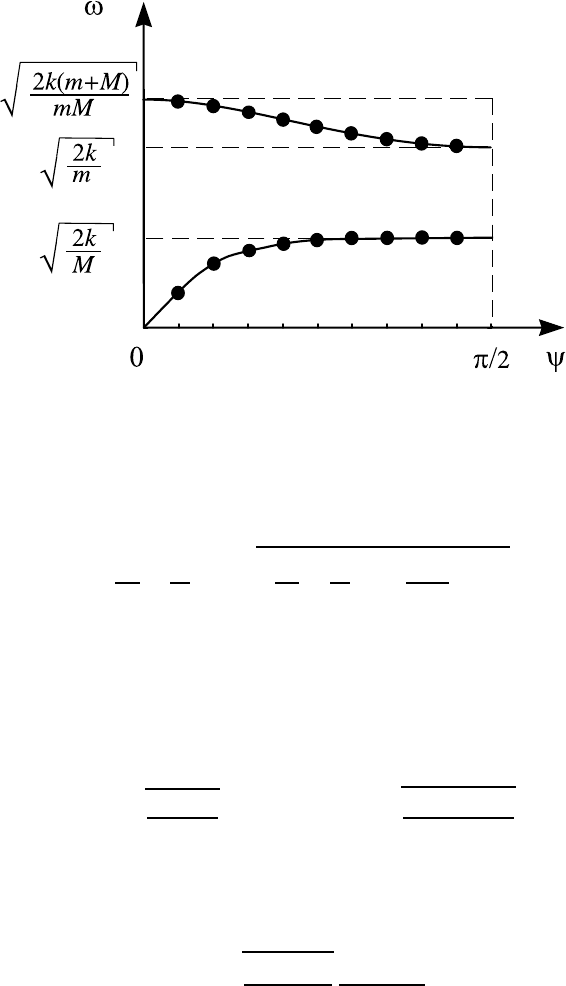
Рис. 8.16. Спектр колебаний цепочки "атомов"в одномерной

модели кристалла.

= 0, и вместо (8.85) можно записать

1,2

(ψ) = k









∓





−

sin





. (8.88)

Эти зависимости изображены на рис. 8.16. При больших N собственные

частоты плотно заполняют обе ветви спектра. Характер спектра при этом

несколько изменяется. При малых ψ второе слагаемое под корнем гораздо

меньше первого, и корень можно разложить в ряд. В этой части спектра,

с учетом того, что sin ψ ≈ ψ  1 получаем

(ψ) ≈

m + M

ψ , ω

(ψ) ≈

2k(m + M)

. (8.89)

Низкочастотная ветвь ω

(ψ) при малых ψ ведет себя как отрезок прямой,

выходящей из начала координат. Для самой низшей моды (j = 1) отсюда

следует, что

(ψ

) =

(m + M)

(2N + 1)

Если число “атомов” очень велико (N ∼ 10

), то эта частота отличается

на много порядков от ω

. Для низкочастотной ветви частота колебаний

206

линейно увеличивается с номером моды, а для высокочастотной — оста-

ется постоянной. В первом случае часто говорят об акустических колеба-

ниях, или дебаевской ветви спектра, а во втором — об оптической ветви,

поскольку соответствующие частоты лежат обычно в инфракрасном диа-

пазоне.

На другом краю спектра следует положить sin ψ ≈ 1, тогда

(ψ) ≈

, ω

(ψ) ≈

. (8.90)

Между этими значениями других собственных частот системы нет.

В случае, если массы “атомов” значительно отличаются (M  m),

то можно считать, что оптическая ветвь идет практически параллельно

горизонтальной оси, так как ширина полосы, в которой она лежит, равна

∆ω =

2k(m + M)

−

≈

. (8.91)

Для расчета плотности спектра частот ρ(w) проще всего воспользо-

ваться формулой (8.81). Дифференцируя соотношение (8.88), и опуская

несущественный постоянный множитель, получаем

ρ(ω) ∼

ω |ω

− Ω

(ω

− Ω

)

− [(M −m)/(M + m)]

Ω

− (ω

− Ω

)

(8.92)

где Ω

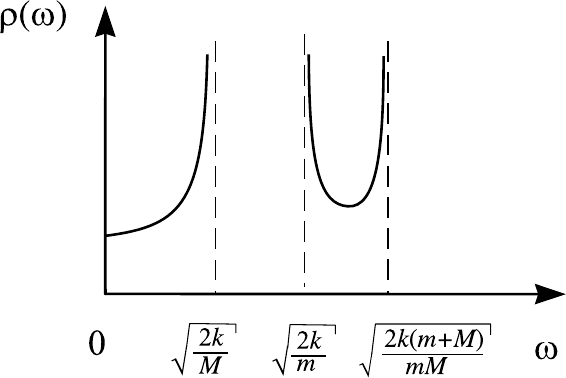
= k(1/m+1/M). Эта функция изображена на рис. 8.17. Видно, что

плотность собственных частот отлична от нуля на двух интервалах оси ω,

совпадающих с положением акустической и оптической ветвей спектра.

Вблизи граничных точек функция ρ(ω) имеет сингулярности, однако это

не относится к точке ω = 0, т. е. к нижней границе акустической ветви,

так как в этой точке dω/dψ 6= 0.

Рассмотренные примеры показывают, что вид спектральной плотности

ρ(ω) в значительной степени определяется дискретной структурой среды,

и зависит от количества “атомов” разных типов на одном периоде систе-

мы, а также их масс. То же самое можно сказать о реальном твердом

теле. Функция ρ(ω) допускает прямое измерение в эксперименте, напри-

мер, с помощью дифракции медленных нейтронов на кристалле, и, таким

образом, она служит источником информации о строении вещества.

207

Рис. 8.17. Плотность распределения частот для одномерной

модели кристалла в виде цепочки из “атомов” двух типов.

ГЛ АВА 9

Переход к одномерной сплошной среде в цепочке

связанных осцилляторов. Волны. Дисперсия

Вводные замечания. Что же такое волна? Несколько опре-

делений. Об истории коронации одной русской императрицы.

Еще определения. Что можно сказать о свойствах волны? На-

поминание о волновой терминологии. Общее линейное урав-

нение. Дисперсионное соотношение. Диспергирующие волны;

групповая скорость. С чем связано существование диспер-

сии в среде? Пространственная и временная дисперсия (су-

ществование в среде собственных пространственных и вре-

менных масштабов); нелокальная связь физических величин;

зависимость диэлектрической пронизаемости от частоты и

волнового числа). О квазичастицах.

§ 1. Вводные замечания

Цепочка связанных осцилля торов представляет собой простейшую

упорядоченную структуру. Простыми примерами модели упорядоченной

структуры, в которой тождественные осцилляторы связаны между собой

не любым, а определенным образом, могут служить линейная цепочка из

одинаковых частиц, расположенных вдоль прямой на равных расстояниях

друг от друга (одномерная решетка из одинаковых частиц); механическая

система, состоящая из набора связанных пружинами маятников; цепочка

из LC — элементов; бесконечный ряд одинаковых акустических резо-

наторов; цепочка, образованная из магнитов, и др. В частности, систе-

ма, правильно расположенных в пространстве шариков, связанных друг

с другом пружинами, представляет собой грубую модель твердого тела

(см., например, в [1] главу “Коле ба ния решетки”). Показательно в этом

смысле начало упомянутой главы. “Простейшее твердое тело — это, по-

видимому, твердый аргон. Он состоит из правильно расположенных ней-

тральных атомов с крепко связанными электронными оболочками. Эти

209

атомы удерживаются вблизи друг друга силами Ван-дер Ваальса, ко-

торые действуют в основном между ближайшими сосед ями в решетке.

Физические процессы в таком кристалле связаны с тепловым движени-

ем атомов вблизи своих идеализированных положений равновесия. Для

простейшего описания такого движения используется модель Эйнштейна,

согласно которой каждый атом колеблется подобно простому гармониче-

скому осциллятору в потенциальной яме, образованной силами его взаи-

модействия с соседями”

. Если в такой одномерной решетке один шарик

сместить из положения равновесия, то будут смещаться и соседние — по

всей упорядоченной структуре побежит волна. Волны, бегущие в твер-

дом теле или другой упорядоченной структуре, характеризуются длиной

волны λ и частотой ω, которые удовлетворяют закону дисперсии

ω = ω(k), (9.1)

k = 2π/λ. Из соотношения ((9.1)) следует, что волна с определенным

вектором k имеет и определенную частоту; это позволяет рассматривать

волну как осциллятор, совершающий колебания с частотой ω(k). Тогда

приходим к аналогии между поведением твердого тела и “газа” осцилля-

торов, движущихся независимо друг о т друга (см.,например [2]). Прав-

да, в движении нового элементарного осциллят ора участвуют все атомы

твердого тела. Волне (осциллятору) можно поставить в соответствие ква-

зичастицу с энергией E = ~ω(k) и импульсом p = ~k. Таким образом,

анализ поведения колебаний в упорядоченных структурах приводит нас

к одному из самых интересных понятий современной физики — понятию

квазичастиц [3].

Вернемся к цепочке одинаковых маятников, связанных между собой

пружинами (см. рис. 8.9)

. Пред положим, что пространственный пери-

од волнового движения в дискретной цепочке много больше расстояния

между маятниками, т.е. много больше размера ячеек. Тогда возможны

Интересно, что Джон Уильям Рэлей — основоположник линейной теории колебаний

и волн получил в 1904 году Нобелевскую премию за открытие в 1894 году вместе с

Уильямом Рамзаем нового химического элемента — аргона, за исследование его свойств

и определение места в периодической системе элементов.

В этой главе мы будем обозначать углы отклонения маятников через ϕ

, а жест-

кость связывающих их пружин через γ, чтобы не возникло путаницы со стандартными

обозначениями, принятыми в теории волн

210

следующие замены:

(t) → ϕ(x, t) ,

n+1

(t) −→ ϕ{(x + a), t} = ϕ(x, t) +

∂ϕ(x, t)

∂x

a +

∂

ϕ(x, t)

∂x

+ . . . ,

n−1

(t) −→ ϕ{(x − a), t} = ϕ(x, t) −

∂ϕ(x, t)

∂x

a +

∂

ϕ(x, t)

∂x

+ . . . .

Переходя от дискретной координаты к непрерывной и используя введен-

ные выше замены в уравнении, получим уравнение в частных производ-

ных

∂

ϕ(x, t)

∂t

− v

∂

ϕ(x, t)

∂x

+ ω

ϕ(x, t) = 0, (9.2)

где v

= γ

/m. Это линеаризованное уравнение Клейна — Гордона,

впервые появившееся в теории поля.

Если в уравнении (9.2) устремить ω

к нулю, то получим обычное

линейное волновое уравнение

∂

ϕ(x, t)

∂t

− v

∂

ϕ(x, t)

∂x

= 0 . (9.3)

Вообще говоря, любая одномерная волна малой амплитуды может

быть описана решением волнового уравнения (9.3), где v = const и имеет

размерность скорости.

Для любых функций F

и F

решениями уравнения (9.3) являются

функции F

(x − vt) и F

(x + vt). Очевидно, что решение

ϕ(x, t) = F

(x − vt) + F

(x + vt) (9.4)

в виде двух волн, распространяющихся навстречу друг другу, также удо-

влетворяют уравнению (9.3).

Введем обозначения ξ = x − vt и η = x + vt. Тогда

∂ϕ

∂x

∂F

∂ξ

∂ϕ

∂t

= −v

∂F

∂ξ

∂

∂x

∂

∂ξ

∂

∂t

= v

∂

∂ξ

Отсюда получаем, что для ϕ = F

(ξ) выполняется уравнение

∂

∂t

− v

∂

∂x

= 0 .