Тіманюк В.О., Животова О.М. Біофізика
Подождите немного. Документ загружается.

31
Знайдемо рівняння фазових траєкторій, для чого поділимо друге
рівняння системи на перше:
(2.5)
або після розділення змінних:
Проінтегрувавши дане рівняння, одержимо:
γ
2
x – ε
2
ln x + γ
1
y – ε
1
lny = C,
де С — стала інтегрування.
Отримане рівняння дозволяє нам, задаючи значення С, побудувати
сімейство фазових траєкторій, але їхній вигляд важко передбачити за-
здалегідь. Дана задача спроститься, якщо ми знайдемо рівняння ізоклін,
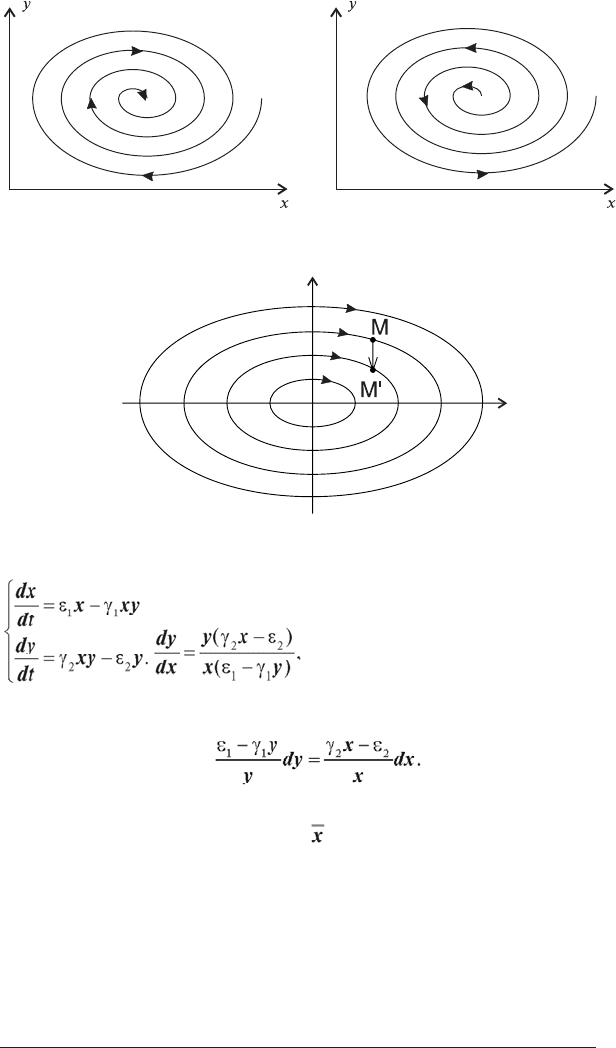
Рис. 2.4. Стійкий (а) та нестійкий (б) фокуси.
y
x
Рис. 2.5. Особлива точка типу “центр”.
32
координати особливих точок і визначимо їхній тип.
З (2.5) випливають рівняння ізоклін:
x = 0; у = ε
1
/γ
1
;
у = 0; х = ε
2
/γ
2
.
Для визначення координат особливих точок прирівнюємо чисельник
і знаменник рівняння (2.5) нулю:
x (ε
1
– γ
1
y) = 0,
y (γ
2
x – ε
2
) = 0,
звідки одержимо:
1
= 0,
1
= 0;
2
= ε
2
/γ
2
,
2
= ε
1
/γ
1
.
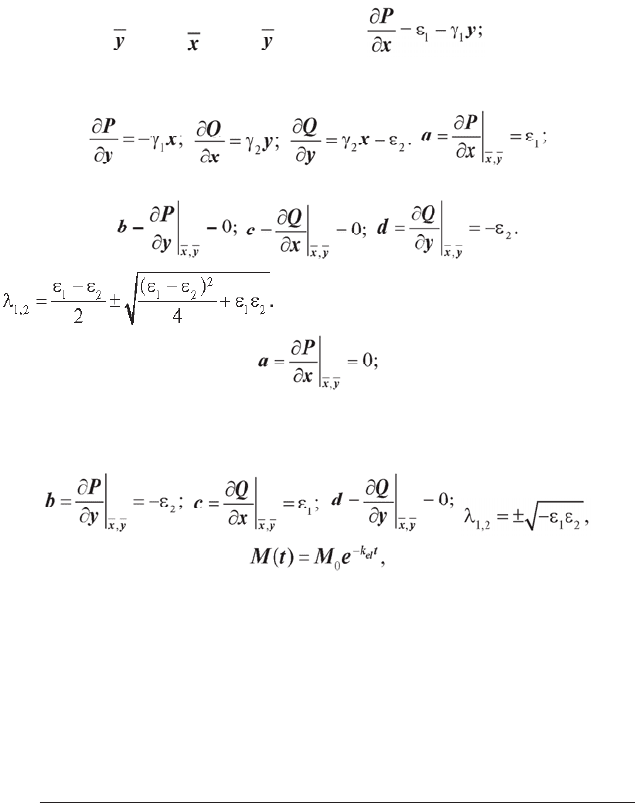
Визначимо тип особливих точок, для чого знайдемо наступні част-
кові похідні:
Тоді для першої особливої точки
З даного рівняння видно, що λ
1
> 0, λ
2
< 0, що відповідає особливій
точці «сідло».
Для другої особливої точки
що відповідає особливій точці типу «центр» (дійсні частини λ дорів-
нюють нулю).
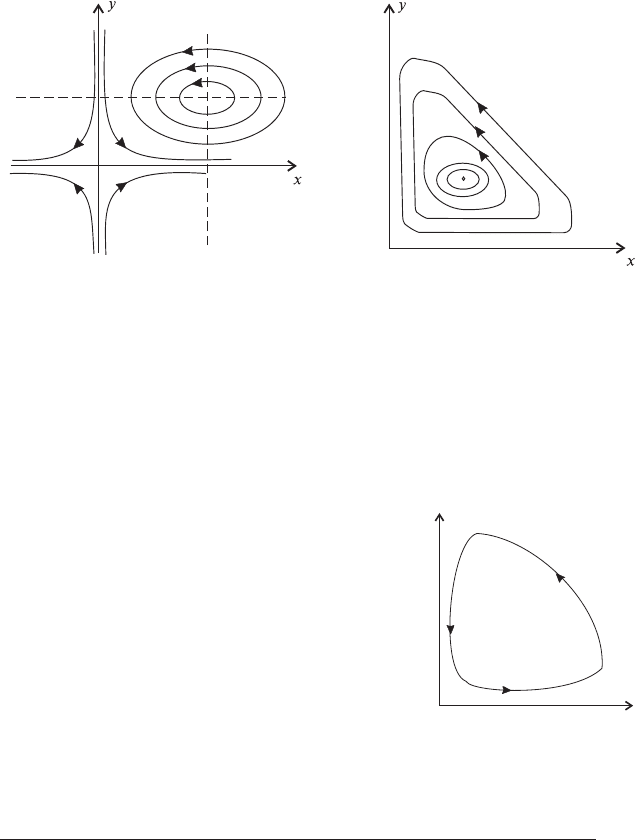
Тепер можна представити загальну картину розташування фазових
траєкторій (рис. 2.6,а). Насправді всі реальні фазові траєкторії розташо-
вуються лише в першому квадранті. Реальний фазовий портрет моделі
хижак — жертва наведений на рисунку 2.6,б.
Кожну фазову траєкторію можна розділити на чотири частини, що
відповідають різним стадіям взаємодії між хижаками і жертвами (рис.
33
2.7). Як видно з рисунка, на першій стадії кількість жертв зменшується, а
кількість хижаків збільшується. Ця стадія називається стадією виїдання
жертви. На другому етапі кількість їжі зменшується настільки, що почи-
нає зменшуватися популяція хижаків. Це стадія вимирання хижака. На
третьому етапі кількість як хижаків, так і жертв така мала, що імовірність
їхньої зустрічі вкрай низька. Кількість жертв починає поступово збіль-
шуватися. Це стадія виходу жертв зFпід контролю хижака. На четвертій
стадії кількість жертв починає інтенсивно збільшуватися, що викликає
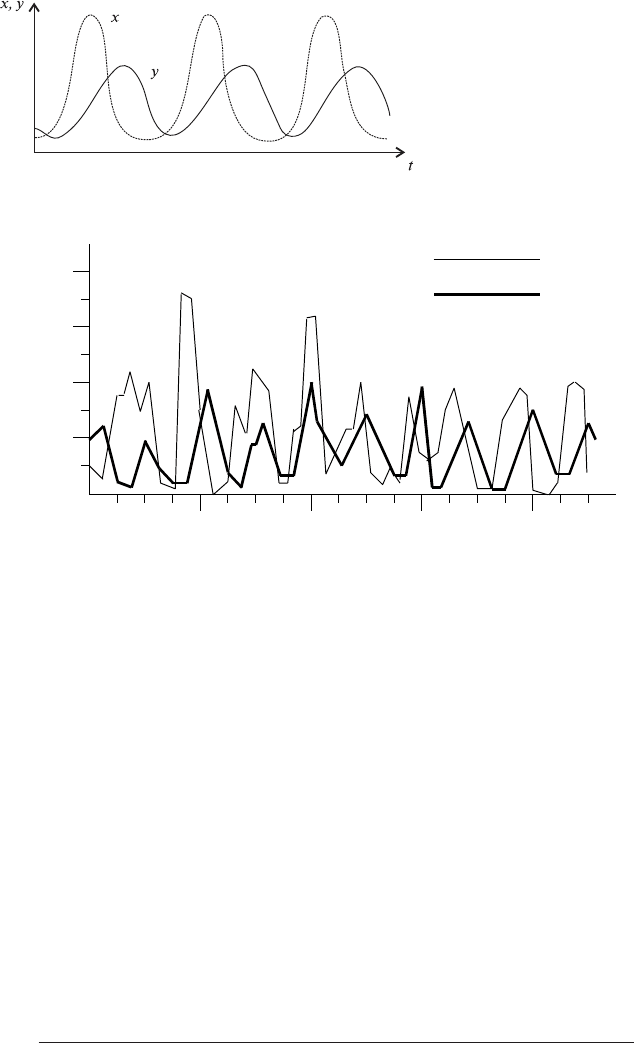
також збільшення, але більш повільне, популяції хижаків. Картина зміни
в часі популяцій хижаків і жертв подана на рисунку 2.8.
Модель Вольтерра більшFменш відповідає даним, узятим із статистики
чисельностей рисей і зайців у Канаді за різні роки (рис. 2.9), однак для
більш точної відповідності в модель уводять ряд поправок.
§ 12. Особливості моделювання фармакокіне-
тичних процесів
Методи математичного моделювання ши-
роко застосовують у фармації. При побудові
деякої математичної моделі неможливо вра-
ховувати всі фактори системи. Математичне
моделювання припускає деяке спрощення
системи і зневагу деталями, що незначно
впливають на процес. Предметом розгляду
фармакокінетики є зміна в часі концентрації
речовини в клітині, органі, тканині або цілому
Рис. 2.6. Фазовий портрет моделі хижак – жертва (пояснення в тексті).
y = ε
1
/γ
1
х = ε
2
/γ
2
а
б
x
y
1
2
3
4
Рис. 2.7. Різні стадії взає-
модії хижаків і жертв між
собою.
34
організмі. При цьому
звичайно не розгляда-
ються причини змен-
шення або збільшення
концентрації препара-
ту, тобто молекулярні
механізми мембранного
транспорту, зв’язування
і руйнації речовини.
При розгляді цілого
організму або якогось органа в якості одиниці системи було б розумно
вибрати клітину. Однак кількість клітин в організмі і навіть в окре-
мому органі така велика, що роз глядати кожну з них неможливо. У
фармакокінетиці звичайно за одиницю системи приймається камера.
Фармакокінетичною камерою називається частина системи, у якій роз-
поділ препарату можна вважати рівномірним. У залежності від задачі,
що розв’язується, за камеру може виступати клітина, орган, тканина і
навіть весь організм.
Припущення про рівномірний розподіл препарату в камері з погляду
фізіології неприпустиме. Однак якщо перевірка показала адекватність
моделі даному процесу, то додаткове введення нових одиниць у роз-
глянуту систему, тобто розбивка фармакокінетичної камери на кілька
камер, не буде сприяти підвищенню точності результатів. Введення
нових камер може бути обумовлено тільки невідповідністю математичної
моделі реальній системі. У залежності від кількості камер фармакокіне-
тичні моделі розділяють на однокамерні, двокамерні та багатокамерні
моделі.
160
120
80
40
1845
1865
1885 1905 1925 Роки
Заєць
Рись
Шкурки (тис.)
Рис. 2.9. Криві чисельності зайця і рисі в Канаді.
Рис. 2.8. Залежність чисельності хижаків у і жертв х
від часу.
35
§ 13. Деякі фармакокінетичні моделі
Припустимо, в організм було введено деякий препарат. Розглянемо
модель його виведення з організму. Організм представимо у ви гляді по-
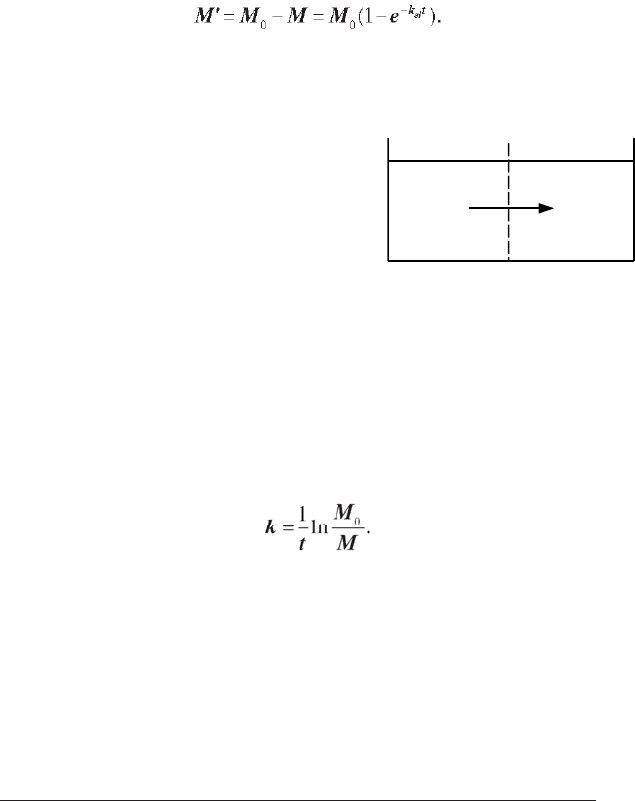
судини А, а навколишнє середовище — у вигляді посудини В (рис. 2.10).
Посудина В має нескінченно великий об’єм, тому імовірність проник-
нення введеного препарату обернено в посудину А мала і з часом увесь
препарат переміститься в посудину В. Дана модель є однокамерною,
тому що весь організм поданий у вигляді однієї камери.
Можна показати, що зміна кількості препарату в організмі описується
наступним експоненціальним рівнянням:
(2.6)
де М
0
— кількість введеного в організм препарату в початковий момент
часу t = 0; М — кількість препарату в організмі в довільний момент часу
t; k
el
— константа швидкості елімінації.
Елімінацією називається сукупність
процесів, що сприяють зменшенню
концентрації препарату в організмі. До
таких процесів відносяться виведення
препарату нирками, кишечником, леге-
нями (у випадку летучих речовин), хімічні
перетворення і необоротне зв’язування, що
приводять до втрати біологічної активності.
Так як М зменшується в часі, то показник
експоненти має знак “мінус”. З (2.6) видно, що на початку процесу пре-
парат буде виводитися швидко, але поступово швидкість цього процесу
зменшиться. Сумарна кількість препарату в обох посудинах залишається
незмінною, тобто
М + М’ = М
0
,
де М’ — кількість препарату в навколишньому середовищі.
То ді
(2.7)
З (2.6) і (2.7) випливає, що при t = 0, М = М
0
, М’ = 0, а при t →∞,
навпаки, М = 0, а М’ = М
0
. Графіки функцій (2.6) і (2.7) приведені на
рис. 2.11.
Прологарифмувавши (2.6), дістанемо наступне:
ln M = lnM
0
– k
el
t. (2.8)
Дане рівняння дозволяє перейти від експоненціальної залежності
до лінійної (рис. 2.12) і обчислити константу швидкості елімінації (або
будьFякого іншого процесу), якщо відома початкова кількість речовини
А
В
Рис. 2.10 (пояснення в тексті).

36
і кількість речовини в деякий момент часу t
Обчислимо миттєву швидкість зміни кількості препарату, для чого
продиференціюємо вирази (2.6) і (2.7) за часом. Тоді для деякого моменту
часу швидкість виведення препарату з однієї камери дорівнює
(2.9)
і швидкість його накопичення в другий
Розв’язком отриманих диференціальних рівнянь є вирази (2.6) і
(2.7).
Припустимо, що перегородка між камерами А і В пропускає препарат
в обидві сторони, але з різною швидкіс-
тю (за посудини А і В тут ви ступають не
організм і навколишнє середовище, а,
наприклад, орган і кров). У цьому випад-
ку кількість препарату в камері А не буде
дорівнювати кількості цього препарату в
камері В. Рівняння язміни кількості пре-
парату в камері А прийме вигляд:
де М
А
і М
В
— відповідно, кіль-
кості препарату у камерах А та В;
k
АВ
— константа швидкості переносу пре-
парату з камери А в камеру В; k
ВА
— конс-
Рис. 2.11. Зміна кількості препарату в посудинах А (рис. а) і
В (рис. б) у часі.
t
t
M
M’
M
0
M
0
а
б
t
ln M
ln M
0
Рис. 2.12. Залежність кількості
препарату в посудині А від часу в
напівлогарифмічних координатах.
37
танта швидкості переносу препарату з камери В в камеру А.
Через деякий проміжок часу між камерами встановиться рівновага,
тобто концентрація препарату не буде змінюватися в часі:
З цієї умови випливає рівність
де і — кількості речовини в камері А і В, відповідно,
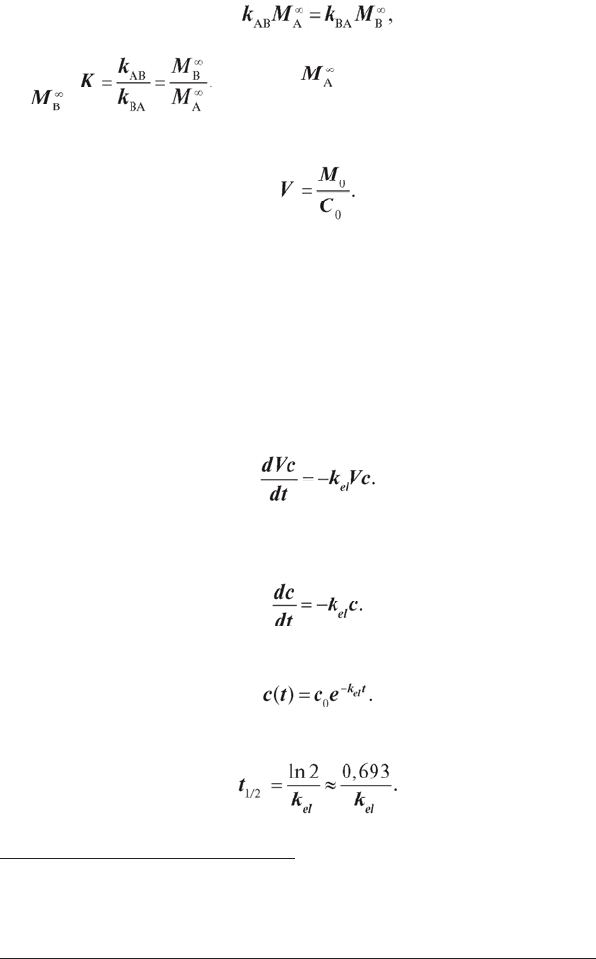
після настання рівноваги. З останнього рівняння можна одержати вираз
для константи рівноваги К:
Від кількості препарату М зручніше перейти до його концентрації
с:
M(t) = Vс(t), (2.10)
де V — уявний об’єм розподілу препарату. Уявний об’єм не відпо відає
реальному об’єму тканини, а є лише коефіцієнтом пропор ційності між
кількістю препарату і його концентрацією в тестFтканині
1
. Величину V
можна обчислити, розділивши кількість препарату в будьFякий момент
часу на концентрацію в цей же момент. Зручніше V обчислювати при
t = 0:
Якщо весь уведений препарат поступає у розглянуту камеру, то М
0
дорівнює дозі препарату.
Підставимо (2.10) у (2.9):
Скоротивши на постійну величину V, отримаємо
Розв’язок цього рівняння
lnc = lnc
0
– k
el
t, (2.11)
або
Важливим параметром процесу є період напіввиведення препарату
t
1/2
, тобто час, протягом якого концентрація препарату в камері зни-
жується вдвічі. Підставимо в рівняння (2.11) замість концентрації c
1
Тест[тканина – тканина, у якій визначається концентрація препарату в ході дослідження.
Найчастіше тест[тканиною є кров.
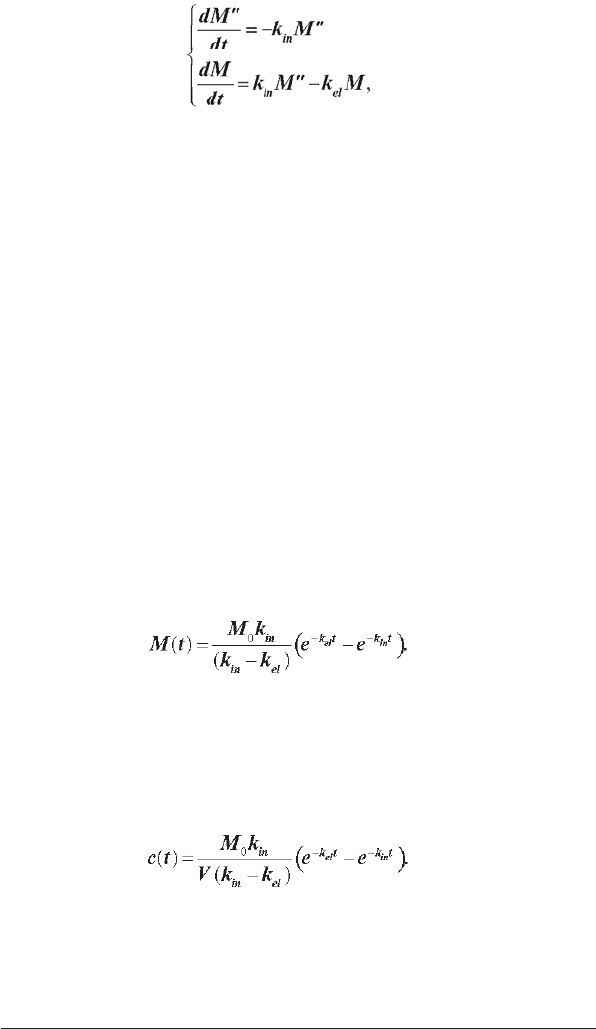
38
концентрацію c
0
/2:
lnc
0
/2 = lnc
0
– k
el
t
1/2
,
звідки отримаємо
Іншим параметром, що характеризує процес, є кліренс Cl, який
дорівнює об’єму тестFтканини, що звільняється від препарату за оди-
ницю часу. Ця величина дорівнює добутку уявного об’єму на константу
елімінації
Cl = Vk
el
.
Критерієм застосовності одночастинної моделі для вивчення фар-
макокінетики препарату є можливість лінеаризації даних у координатах
«lnc – t», «dc/dt – c» або «lndс/dt – t».
Лікарські препарати часто вводять не безпосередньо в кров, а в інші
тканини. Але як тестFтканина, як і раніше використовується кров. У
цьому випадку концентрація препарату в крові досягає максимального
значення не відразу, а лише через деякий час. Тому графік залежності
концентрації препарату від часу в напівлогарифмічних координатах має
лінійний характер лише після досягнення максимальної концентрації
(рис. 2.13).
Для таких процесів крім основної камери, що моделює кров та інші
тканини, у які проникає препарат, вводять підкамеру, що моделює
тканину — місце введення препарату. Для опису такого процесу вже
потрібна система з двох рівнянь:
(2.12)
де М’’ і М — кількість препарату в підкамері й основній камері відпо-
відно; k
in
— константа усмоктування препарату з підкамери в основ-
ну камеру; k
el
— константа елімінації препарату з основної камери.
Проінтегрувавши (2.12) з урахуванням початкових умов
(М’’(0) = М
0
, М(0) = 0), одержимо рівняння зміни кількості препарату
в основній камері:
Так як M = cV,
де c — концентрація препарату в основній камері; а V — її уявний об’єм,
то залежність концентрації від часу має наступний вигляд:

39
(2.13)
Знаючи параметри k
in
, k
el
, V і М
0
, по рівнянню (2.13) можна розраху-
вати концентрацію препарату в будьFякий момент часу.
Введемо позначення
Тоді рівняння (2.13) запишеться у вигляді:
(2.14)
У випадку, коли усмоктування препарату відбувається набагато швид-
ше його виведення (k
in
>> k
el
), при великих значеннях t членом рівняння
ехр (–k
in
t) можна зневажити. Тоді рівняння (2.14) спрощується:
У цьому випадку низхідна частина залежності (рис. 2.13) ха-
рактеризує в основному елімінацію препарату. Якщо ж, навпаки,
швидкість усмоктування набагато менша швидкості виведення
(k
in
<< k
el
), рівняння (2.14) зводиться до вигляду:
а низхідна частина кривої характеризує в основному процес усмокту-
вання.
Якщо ж константи усмоктування і виведення мають однаковий поря-
док, то обидві частини кривої характеризують як елімінацію препарату,
так і всмоктування його.
Знайдемо час t
max
, протягом якого досягається максимальна концен-
трація с
max
, для чого продиференціюємо вираз 2.14:
Щоб знайти максимальне значення функції, прирівняємо цей вираз
нулю
звідки знайдемо t
max
:

40
(2.15)
З останнього рівняння видно, що час досягнення максимальної кон-
центрації не залежить від дози введеного препарату, а цілком визначається
константами усмоктування і виведення. Підставивши (2.15) у (2.13), мож-
на визначити максимальну
концентрацію препарату в
основній камері.
Для багатокамерних мо-
делей потрібно складати
систему з кількох диферен-
ціальних рівнянь. Концен-
трація препарату в якомусь
органі залежить від швид-
костей кількох процесів,
кожний із яких характери-
зується власною констан-
тою k:
1) від швидкості всмок-
тування препарату з міс-
ця введення (наприклад, з
кишечника) у кров, якщо
було відсутнє безпосереднє
введення ліків в кровоносне
русло (константа k
12
);
2) від швидкості транспор-
ту препарату з крові в орган
(константа k
23
);
3) від швидкості зворотного процесу: транспорту препарату з органа
в кров (константа k
32
);
4) від швидкості виведення препарату з організму видільною систе-
мою (константа k
4
).
Кожний орган, у якому може знаходитися препарат (кишечник, кров,
органFмішень, видільні органи) представимо у вигляді окремих блоків
(камер) (рис. 2.14), у кожному з яких розподіл препарату однорідний.
На даному етапі вже можна скласти систему диференціальних рів-
C, мкг/мл
t, год
102345
10
100
Рис. 2.13. Апроксимація даних фармакокінетики це-
фалексину в сироватці крові мишей, які одержували
препарат усередину в дозі 400 мг/кг, однокамерною
моделлю з усмоктуванням (k
in
=
= 4,60 1/год., k
el
= 0,90 1/год.).
