Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2

Подождите немного. Документ загружается.

§2.

Диференціальне числення функцій багатьох змінних

361

1 2

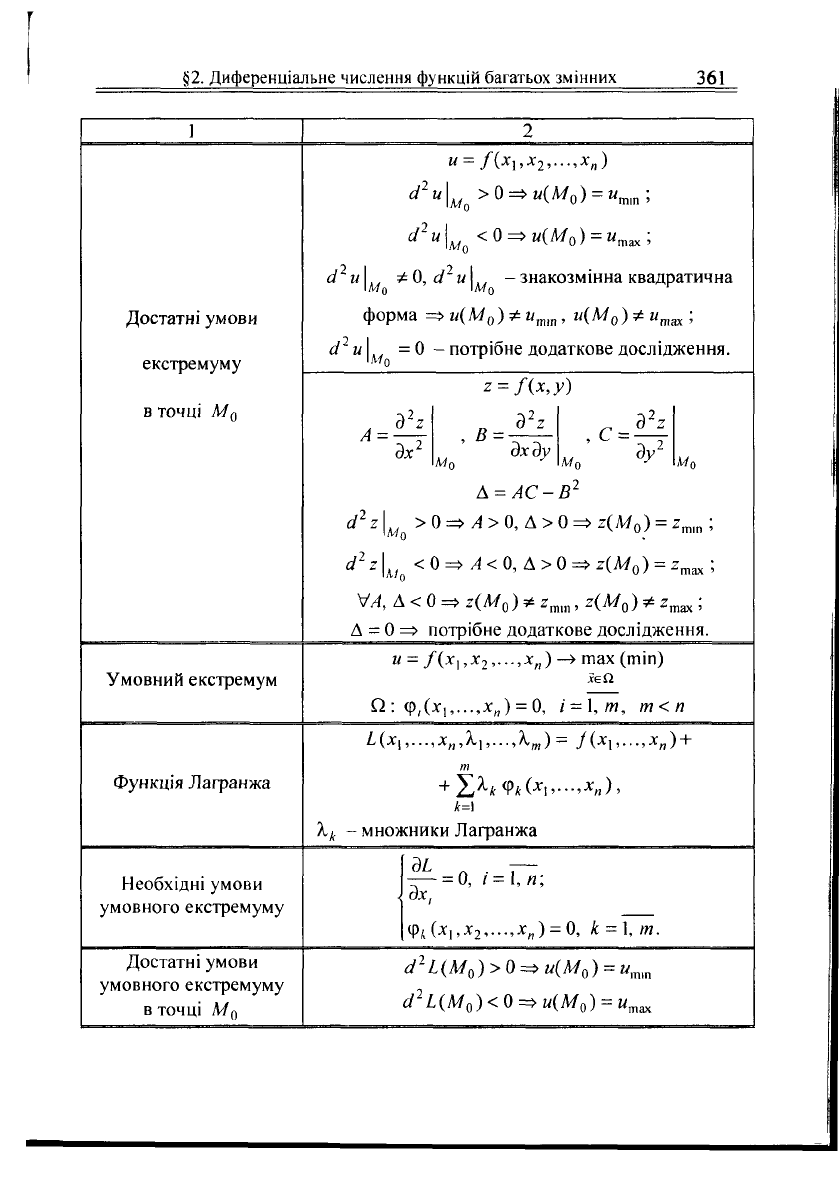
Достатні умови

екстремуму

в точці М

/(х

,...,х

)

^"Ц,

=*"(

^о)

"т,п

"Ц

<0=>М

(

Л/

о)

"тах;

и\

Ф0,сі

и\

-знакозмінна квадратична

форма

=>и(М

)Фи

тт

и(М

)*и

тах

;

сі

и\

= 0 - потрібне додаткове дослідження.

Достатні умови

екстремуму

в точці М

дх

дхду

ду

Мгу

м$

А = АС-В

^Лщ >0=>/І>0,Д>0=>

(М

) =

тіп

;

сі

к1о

<0=>/К0,Д>0=>2(Л/

) =

тах

;

\/А,

А < 0 => г(М

) * 2

тт

, г(М

) *

тах

;

д = 0 => потрібне додаткове дослідження.

Умовний екстремум

/(х\,х

,.--,х

) —>

шах (тіп)

О : ф,(х,,...,х

) = 0, і = \,т, т<п

Функція Лагранжа

І(х,,...,х„ Д,,...Д„,) = /О,,...,*„) +

+ ^к

Рк(х

]

,--;Х

к=\

- множники Лагранжа

Необхідні умови

умовного екстремуму

•

дх,

(х

,х

,...,х„)

= 0, к = \,т.

Достатні умови

умовного екстремуму

в точці М

а-

ЦМ

)>0=*и(М

) = и

шп

сі

ЦМ

)<0=^и(М

)

так

362

Глава 6, Довідковий матеріал

§3. Кратні інтеграли

Таблиця 3.1 - Подвійний інтеграл та його застосування

Поняття

або

співвідношення,

що визначаються

Формула

Подвійний інтеграл

від функції Дх,у)

по області й

\\Дх,у)сіхсіу =

1ітХ/(^,ті,)А5,

Обчислення подвійного

інтеграла:

а) область й:

%(х)<у <ф

(*),

а<х<Ь;

б) область Б:

у,0)<х<\|/

0),

с<у < сі .

\\Дх,у)сіхсіу = \ах \Дх,у)ау

О а <р,(»

Обчислення подвійного

інтеграла:

а) область й:

%(х)<у <ф

(*),

а<х<Ь;

б) область Б:

у,0)<х<\|/

0),

с<у < сі .

Ц/(х, у) сіх сіу = 1 сіу ІДх,у)ах

» С VI (V)

Якобіан перетворення:

\х = х([и,у),

\у =

у(и,у).

/ =

дх дх

ди ду

ду ду

ди ду

Заміна змінних

у подвійному інтегралі:

а) перехід до криволінійних

координат м та V

їх = х(и, у),

\у =

у(и,у).

\\ Дх, у) сіх ф = Л Дх(и, у), у(и,

У))\І\сіисіу

б) перехід до полярних

координат р та ф

\х = рсозф,

[у = р$іп ф,

0<р< +

°°,

0<ф<2л.

Л д*» 7) ^

*=Л/(р

со3

ф>

5іп

ф) р

ф<*р

§3.

Кратні інтеграли

363

Продовження таблиці

3.1

в) перехід

до

узагальнених

полярних координат

\х

ар

СОБ

ф,

[у

йр5Іпф,

я>0, Ь>0

< р

< +

°°,

0 < ф< 2л

||/(х,

у) ах ау =

||/(ар созф,

Ьр

зіп ф)

аЬр фйф

Площа

5/,

області

ОсК Я„

=Цахау

Об'єм тіла

О ,

обмеженого

поверхнями:

о,: г =

Дх,у)>0,

Р^°і

= °>

г = 0,

: циліндрична поверхня

з твірною, паралельною

осі

Ог , і

напрямною

І -

межею області

£>

\\Дх,у)сіхсіу

| 2 =

,у)

О.

Об'єм тіла

Є ,

обмеженого

поверхнями:

а,: г =

/,(*,у),

= /2

(*,>>),

Р*Оу

Рх«у

= О .

||[/2(У^)-/і(У^)]^

Площа

поверхні

а:г =

/(х,у),

пр

хОу

=ц

/і+/;

(х,у)+/;

(х,

/)йхй>

Маса

матеріальної

пластинки ВсК

з густиною \і.(х,у)

\І(Х,

у) сіх сіу

Середня густина и.

сер

матеріальної пластинки,

яка

має масу

т ,

площу

5 і

густину

\і(х, у)

т _

Нхер ~

—

^(х, у) сіх сіу

||сіхау

364

Глава 6. Довідковий матеріал

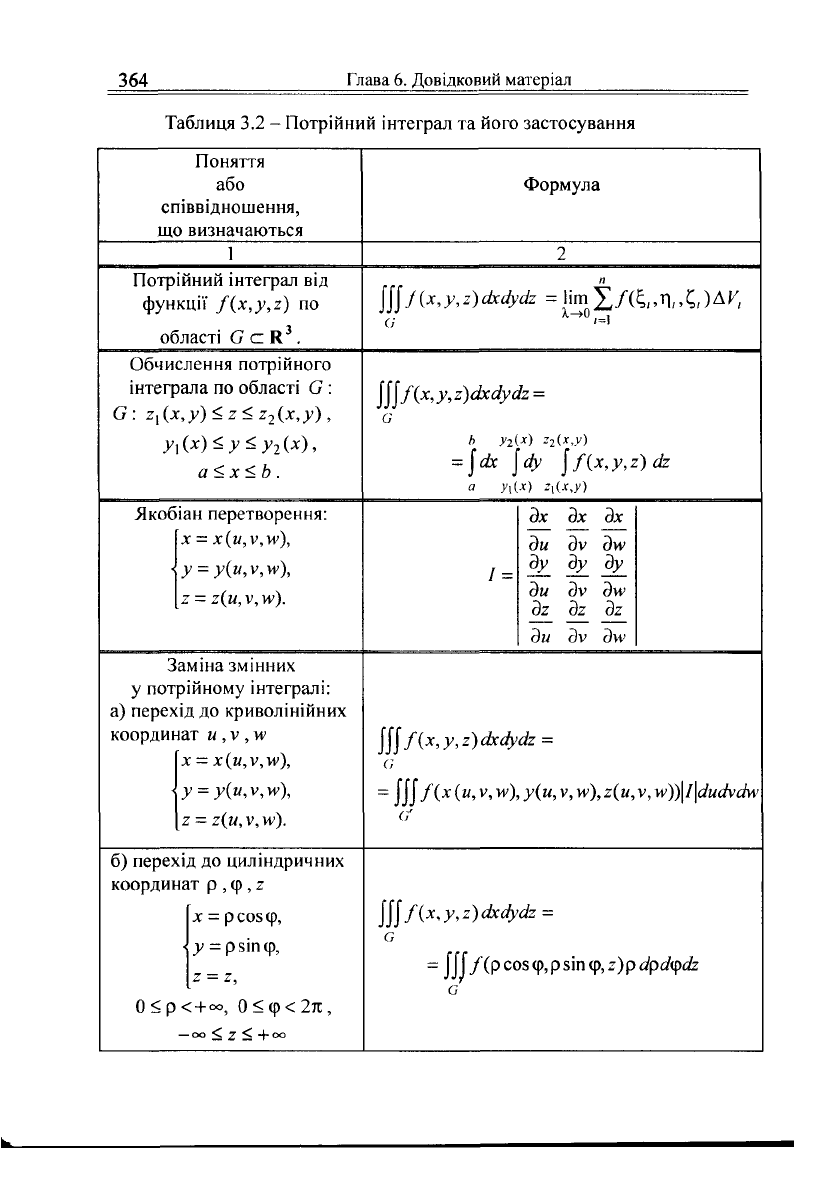
Таблиця 3.2 - Потрійний інтеграл та його застосування

Поняття

або

співвідношення,

що визначаються

Формула

1 2

Потрійний інтефал від

функції

/(х,у,

г)

по

області СсК

{[[

(х,

у,

ахаусіг

Ііт

ті,,

С,)

АУ,

Обчислення потрійного

інтефала по області 0 :

С:

{

{х,у)<г<г

(х,у),

У](х)

(х),

а<х<Ь.

\\\Кх,у,2)ахсіу(І2

Уг(х)

(х,у)

= |ох

\<іу \/{х,у,г)аг

У\(х)

ц(х,у)

Якоб

ан перетворення:

х = х(и,

У,\У),

у(и,у,

и>),

2 = г(и, У,\У).

Зх Зх Зх

ди

ЗУ 3>У

ду

ду ду

ди

ЗУ

дм?

дг

дг дг

ди

ЗУ

дм>

у ПОТ|

а) перех

координ

аміна змінних

зійному інтефалі:

ід до криволінійних

ат и, V ,

м>

х = х(и,у,и'),

у = у(и, У,Ц>),

г(и,

м/).

\\\ї{х,у,2)ахаусІ2

= |Ц/(Х(И,У, їт),у(м,у, н

),2(м,у,н

))|/|^мйуаи'

б) перех

координ

0<р

ід до циліндричних

ат р , ф, 2

= р

СОЗ

ф,

•

у = рзіпф,

= 2,

< +

<*>,

0<ф<2гс,

— оо

< 7 <

+ оо

= Д|/(рсозф,рзіпф,2)рфй?фа2

§3,

Кратні інтеграли

365

Продовження таблиці 3.2

в) перехід до сферичних

координат г, ер, 6

ЇХ

= ГС05ф5Іп6,

<у =

Г8ІПф8ІП0,

= гсозб,

0<г<

оо,

0<ф<2л,

О<0<

]]\/(х,у,2)ахсіусіг =

= Щ /(г соз

зіп 9, г зіп

зіп 9, г соз 9) г

зіп 9 йгсіусВ

Об'єм V тіла СсВ

V =Д[ сіхау•ск

Маса т тіла СсК

з густиною \і(х,у,г)

т =

її\\^(х,у,2)ахсіусІ2

Середня густина ц

сер

тіла,

яке має масу т, об'єм V і

густину [і(х,у,г)

Д[ц(х, у, 2) сіхсіуск

Цсер

\\\сЬссіусІ2

366

Глава 6. Довідковий матеріал

§4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія

поля

Таблиця 4.1 - Криволінійні інтеграли

Поняття

або

співвідношення,

що визначаються

Формула

1 2

Криволінійний інтеграл першого роду

Криволінійний

інтефал першого роду

від функції /(х,у,г)

по дузі А В

ЇДх,у,х)сіІ = \іт^ДМ

)М

АВ

-»°/=1

Обчислення криволінійного інтефала першого роду

а) АВ

АВ:

•

сК

х—х(і),

У =

У0),

2 =

2(Ґ),

1\ ^И1

\Дх,у,г)сіІ =

АВ

= ) Л 40,

у(0,2(0]л/^'

(0 + у'

(0 + 2'

(0 сії

'і

б) АВаК

\х =

х(1\

АВ:

\у=у(і), її

йійі

АВ :у

у(х), а < х < Ь

АВ

х(у), с < у

сі

АВ :р = р(ф), а < ф < |3

\Ях,у)сіІ =

)ЯХ(І),У(І)]УІХ'

(І)

У'

(І)

сії

АВ

б) АВаК

\х =

х(1\

АВ:

\у=у(і), її

йійі

АВ :у

у(х), а < х < Ь

АВ

х(у), с < у

сі

АВ :р = р(ф), а < ф < |3

\Г(х,у)сіІ =\Ях,у(х)]4\

у'

(х)

сіх

АВ

б) АВаК

\х =

х(1\

АВ:

\у=у(і), її

йійі

АВ :у

у(х), а < х < Ь

АВ

х(у), с < у

сі

АВ :р = р(ф), а < ф < |3

<1 і

І/(х,у)<ІІ

=\Ях(уІу]уІх'

(у)

\ сіу

АВ

б) АВаК

\х =

х(1\

АВ:

\у=у(і), її

йійі

АВ :у

у(х), а < х < Ь

АВ

х(у), с < у

сі

АВ :р = р(ф), а < ф < |3

\Ях,у)<іІ =

АВ

Р ,

= \/(Р(ф)соз ф,р(ф)зіп ф)д/р

(ф) + р'

(ф) СІЧ?

а) ДОЕ

Застосування криволінійного інтеграла першого роду

а) ДОЕ

жина / дуги АВ

і=\а

АВ

§4.

Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля 367

Продовження таблиці 4.1

б) маса т матеріальної дуги

АВ з густиною

ц=іі(х,у,г)

|ц(х,

у,2~)йІ

АВ

Криволінійний інтеграл другого роду

Криволінійний інтеграл

другого роду від

вектор-функції

Р(х,у,г)=

=Р(х,у,2)і^(х,у,2)]+К(х,у,г)к

по дузі А В

\Рах+Оау+КсІ2

= Ііт £(?(МД Д^)

АВ

^°і=1

Обчислення криволінійного інтеграла другого роду

а)

АВсК

АВ:х=х(і\у=у{1),2=2{і),

змінюється від і

до і

$Р(х,у,2)ах+(2(х,у,г)ау+К(х,у,2)а2=

АВ

'в

\[Р{Х(1),У((),2(1))Х'{1)

'А

б) АВаК

АВ:х

х(1), у

у(і),

змінюється від і

до і

;

АВ:у = у(х),

х змінюється від х

до х

;

АВ

х(у),

у змінюється від у

до у

\Р(х,у)сіх

<2(х,у)ау =

АВ

'Я

\{Р{х(і),у(і))х\і)+а(х(і\у{())у\

)\а'і

'А

б) АВаК

АВ:х

х(1), у

у(і),

змінюється від і

до і

;

АВ:у = у(х),

х змінюється від х

до х

;

АВ

х(у),

у змінюється від у

до у

ІР(х,у)ах

+ (2(х,у)ау =

АВ

\[Р(х,у(х))

(2<х,у(х))уХх)]ах

б) АВаК

АВ:х

х(1), у

у(і),

змінюється від і

до і

;

АВ:у = у(х),

х змінюється від х

до х

;

АВ

х(у),

у змінюється від у

до у

\Р(х,у)ах

(2(х,у)ау =

АВ

Ув

\[Р(х(у),у)х'(у)

(2(х(у),у)]сІу

УА

Формула Гріна

§Р(х,у)ах

(2(х,у)ау

1\(^-^)ахау

і п

оу )

368

Глава

Довідковий матеріал

Продовження таблиці

4.1

Застосування криволінійного інтеграла другого роду

а) площа плоскої

області

£>,

обмеженої

кривою

-§уах;

8 =

§хау;

8 =

—§хау-уах

і.

б) робота сили

Р=(Р,(3,Я) вздовж

лінії

§Рах

+ Оау + Каг

і.

Таблиця

4.2 -

Поверхневі інтеграли

Поняття

або

співвідношення,

що визначаються

Формула

Пове рхневий інтефал першого роду

Поверхневий інтефал

першого роду

від

функції

/(х, у, г) по

поверхні

\[/(х,у,2)с1а

= Ііт

£/(М,)Дс,

Обчислення поверхневого інтефала першого роду

а:г

2(х,у),

РхОу<3=

°ху

\\/(х,у,г)аЬ

\\І(х,У,2(х,у))4\

(х,у)

г'

(х,у) ахау

Оху

а: у =

у(х,г),

пр

Ю:

а=О

х:

/{/(>,

.У,

Ц/(х,у(х,2),2)4і

у'

(х,2)

у',

(х,2)

ахсіг

Охг

а.х =

х(у,2),

Ц/(х,у,2)ао

\1/(х(у,2\у,г)4\

х'

(у,2)

х'

(у,2)

аусіг

§4.

Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

369

Продовження таблиці

4.2

1 2

Застосування поверхневого інтеграла першого роду

а) площа поверхні

5 = ДАТ

б) маса матеріальної

поверхні

о з

густиною

Ц=Ц(Х,У,2)

Дц(х,у,2)с/а

Поверхневий інтеграл другого роду

Поверхневий інтеграл

другого роду

від

вектор-

функції

Р(х,у,2)=

=Р(х,у,2)1+()(х,у,2)]+К(х,у,2)к

по стороні поверхні

а,

визначеної одиничним

нормальним вектором

(С05СХ,С05Р,С03у)

= ||(Р соз а + (9 соз р

К соз у)

до =

1іт£сР(Л/

),й(М,))Да,

Обчислення поверхневого інтеграла другого роду

а) проектування

на всі три

координатні площини

о-.2

2(х,у),пр

х0у

= О

ху

о:у

>'(х,2),пр

х0

,о

= І)

хг

а:х

= х(у, 2),

пр^ст

= О

ЦСРсоза+

£созР +

Лсо5у)#а

\\Р(х(у,2\у,2)ауск±

\\(2(х,у(х,2\г)ахаг

\\к(х,у,2(х,у))сіхау

знак вибирається відповідно

до

знаку соз

а,

созр,

созу

на о

б) проектування

на одну

з координатних площин

е>:

2(х,у), пр

х0і

,е>

= О

ху

ахау

г=:(х,у)

а:у

= у(х, 2),

пр

х0

,о

= И

Х2

ахаг

У=У(Х,2)

о:

х = х(у, 2),

пр

х;

,а

у.

•

созсх

у2

і і

ауск

х=х(у,і)

370

Глава 6, Довідковий матеріал

Продовження таблиці 4.2

Формула

Остроградського-Гаусса

Р ауск + () ахск + К сіхау =

гг,(др зд злі. , .

а - зовнішня сторона замкненої поверхні,

що обмежує тіло О

Формула Стокса

§Рсіх +

С;с1у

+ Ка2 =

(

(дО дР V ^ (дК д(3 V .

дг дх )

орієнтація кривої Ь узгоджена з вибором

сторони поверхні о

Застосування поверхневого інтеграла другого роду

Обчислення кількості

рідини П , що протікає

через поверхню о

в одиницю часу в сторону,

визначену напрямом

вектора нормалі п, якщо

Р(Х,У,2)

= У(Х,У,2) -

швидкість руху рідини

П = \\{у,п)сіа