Тесленко О.А. Методы оптимизации. Практикум
Подождите немного. Документ загружается.


МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОСИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНГИЮ
ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ
ЮЖНОГО ФЕДЕРАЛЬНОГО УНИВЕРСИТЕТА В Г. ТАГАНРОГЕ
Факультет автоматики и вычислительной техники
Кафедра систем автоматического управления __
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Дисциплина «Методы оптимизации»
Тема:_____________________________________________
Выполнил
Ст. гр. А-ы Ф. И. О.
Проверил:
Преподавате6ль каф. САУ Ф. И. О.
Таганрог;2008г.
Индивидуальное задание №1
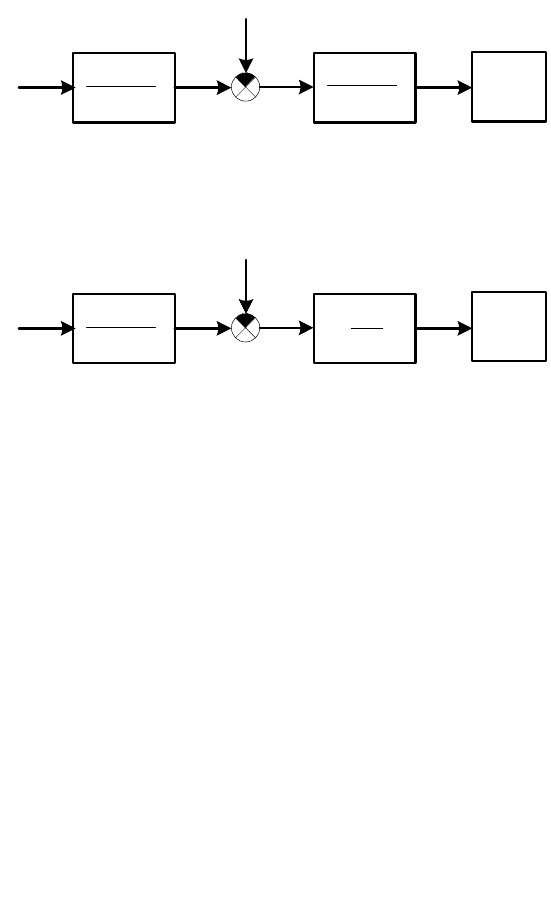
Тема. «Конструирование оптимальной по квадратичному критерию
качества системы программного управления ЭП ДПТ»
1. Структурная схема объекта управления.
1pT
k
у
у
)(tu
)(tf
1
x
2
x
U
я
1pT
k
м
дв
РМ
Структурная схема 1. Управление скоростью вращения выходного вала
ЭП ДПТ.
1pT
k
у
у
)(tu
)(tf
p
k
дв
РМ
2
x
U
я
1
x
Структурная схема 2. Управление поворотом выходного вала ЭП ДПТ.
2. Цель управления. РМ должен переместиться из одного состояния в
другое за определенное время, при минимальных потерях энергии в цепях
управления и якорной цепи ЭД.
3. Критерий качества вида
min)(
22
2
2
2
0
2
1
2
1
dtuxmxmI
k
t
.
4. Возмущающее воздействие вида
)cos()(
0
tatf
.
Требуется определить

1. Аналитическое выражение оптимального программного движения ОУ
)(),(
21
txtx
и оптимального программного управляющего воздействия
)(tu
.
Примечание. Выполняется при
0)( tf
.
2. Произвести моделирование оптимальной системы программного
управления ЭП ДПТ. Построить временную диаграмму:
)(tu
,
)(),(
21
txtx
и
фазовую траекторию.
3. Ввести возмущающее воздействие
)(tf
и произвести моделирование
оптимальной системы программного управления ЭП ДПТ. Построить
временную диаграмму:
)(tu
,
)(),()()(),(
2111
txtxtxttx
и фазовую
траекторию.
Примечание. Амплитуду
a
возмущающего воздействия выбрать
произвольно в «разумных» пределах, а частоту
0
– из интервала
)
t
2
105(
k
.
4. Моделирование системы управления производить с помощью пакета
MATLAB, программу моделирования представить в отчете.
5. Сделать выводы.

Таблица исходных данных.
№
вар
.
В
ид
О
У
ì
T
ñ
y
T
ñ
y
k
äâ
k
ñÂ
ðàä
k
t
ñ
2
1
m
2
2
m
)0(
1
x
)(
1 k
tx
1 1 5 2 1 1
0
2 3.
802
0
.1884
0 1
00
2 2 - 0
.5
1 1
0
0
.5
0.
25
0
.0625
0
4
3 1 3 4 2 5 1
.5
0.
178
0
.689
1
20
0
4 2 - 0
.68
2 1
5
0
.6
0.
0104
0
.0187
3
0
5 1 5 4 1 5 1
.8
9.
216
0
.984
0 1
50
6 2 - 0
.8
3 1
0
0
.3
1.
138
0
.732
2
0
7 1 2 1
0
4 1
2
1
.8
0.
406
4
.604
1
10
0
8 2 - 0
.9
5 1
5
0
.5
0.
1296
0
.388
0
32
9 1 2 6 1 1
0
1
.5
17
.01
6
.02
0 9
0
1
0
2 - 1
.2
8 2
0
4 0.
0137
0
.1271
0
1
1
1 6 1 2 5 0
.8
0.
718
0
.329
8
0
0
1
2
2 - 1
.5
1
0
1
0
1 0.
0144
0
.44
0
23
1
3
1 4 1 8 2 1 4.
913
9
.297
0 6
5
1
4
2 - 2 2
0
1
0
0
.8
0.
01
0
.88
43
0
1 1 8 2 2 1 1 0. 0 1 0
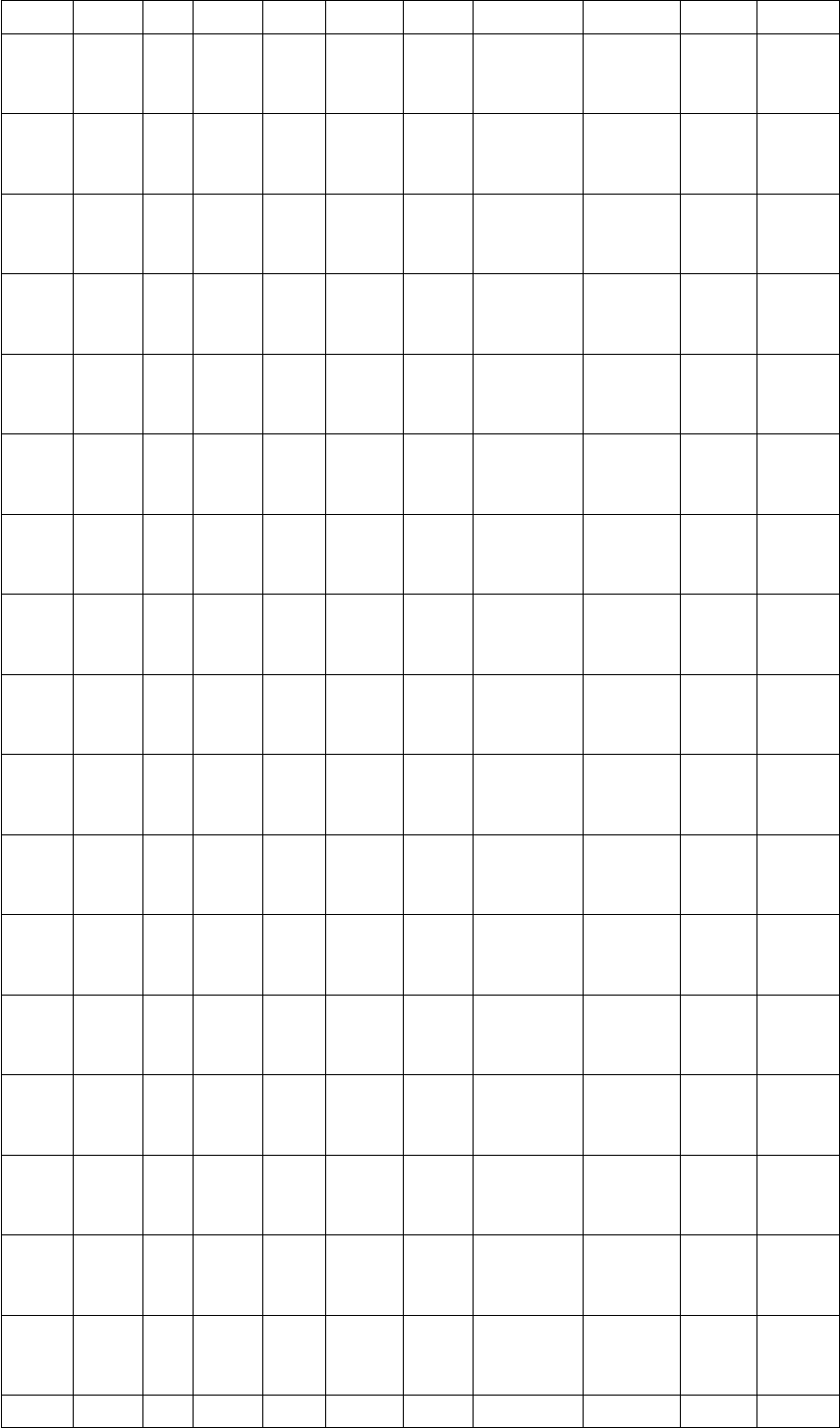
5 2 .4 103 .0273 00
1
6
2 - 0
.25
3
0
5 0
.3
0.
04
0
.996
0
4
1
7
1 4 5 4 1
0
1
.9
0.
569
1
.134
0 1
20
1
8
2 - 3 4
0
2
5
0
.4
0.
0169
1
.4384
3
0
1
9
1 8 4 1 8 1
.8
14
.23
0
.501
1
50
0
2
0
2 - 4 2
0
1
5
0
.5
0.
04
3 0
2
2
1
1 5 2 1 1
0
1 8.
752
0
.234
0 1
10
2
2
2 - 1
5
5
0
2
0
0
.3
0.
912
7
5.94
32
0
2
3
1 3 4 2 5 1
.6
2.
738
1
.969
9
0
0
2
4+
2 - 2
0
1
00
1
0
2 0.
0064
0
.525
0
2
5
1 5 4 5 1 1
.4
60
.826
7
8.360
0 8
0
2
6
2 - 0
.25
1
0
2 0
.3
0.
391
1
.703
23
0
2
7
1 1
0
2 4 1
2
4 0.
245
0
.0731
6
5
0
2
8
2 - 0
.52
1
5
5 0
.15
1.
082
3
.472
0
43
2
9
1 6 2 1 1
0
0
.6
14
2.841
1
.149
0 1
40
3
0
2 - 0
.8
2
.5
8 0
.6
0.
2048
0
.2244
4
0
3
1
1 5 2 1 1
0
0
.8
35
.4816
0
.5084
1
50
0
3
2
2 - 1
,5
1
0
3 0
.7
0.
35
6
.638
0
3
3 1 4 5 4 1 1 1. 1 0 1

3 0 181 .099 25
Примечание.
0)()0(
22
k
txx
.

Таблица исходных данных.
№
вар
.
В
ид
О
У
ì
T
ñ
y
T
ñ
y
k
äâ
k
ñÂ
ðàä
k
t
ñ
2
1
m
2
2
m
)0(
1
x
)(
1 k
tx
1 1 3 4 2 5 4 1
07.666
1
2.703
1
10
0
2 2 - 2
0
1
00
1
0
0
.5
0
.14
1
55.99
45
0
3 1 2 3 5 9 2 0
.3033
1
.293
0 1
20
4 2 - 4
,5
8 1
0
2
.5
3
.24
1
6.19
0
5 1 1
0
2 4 1
2
1
.6
0
.858
0
.159
1
50
0
6 2 - 1
.2
8 2
0
0
.3
0
.0675
0
.286
43
0
7 1 1 3 1
0
9 2
.6
0
.0233
1
.358
0 1
40
8 2 - 0
.25
1
0
2 0
.6
0
.3125
1
.391
2
0
9 1 6 1 2 1
0
1
.8
1
.7701
0
.1097
0 1
30
1
0
2 - 4 2
0
1
5
0
.5
0
.3333
7
.107
0
4
1
1
1 5 4 5 1 3 1
26.36
1
86.906
9
0
0
1
2
2 - 0
.5
1 1
0
2
.5
0
.1
0
.025
45
0
1
3
1 5 2 1 1
0
1
.5
1
.1096
0
.0804
0 8
0
1
4
2 - 1
,5
1
0
5 0
.5
0
,2025
3
,02
0
1
5
1 1 4 2 8 1
.2
4
,5
6
,984
0 6
0
1
6
2 - 2
,5
2
0
1
0
0
.5
0
.293
6
.24
43
0
1
7
1 2 8 1
2
2 2
.5
2 1
11,75
1
10
0
1
8
2 - 5
,2
1
0
1 1
,5
1
.352
1
61.24
0
2
1 1 5 4 1 4 2 1 7 0 1
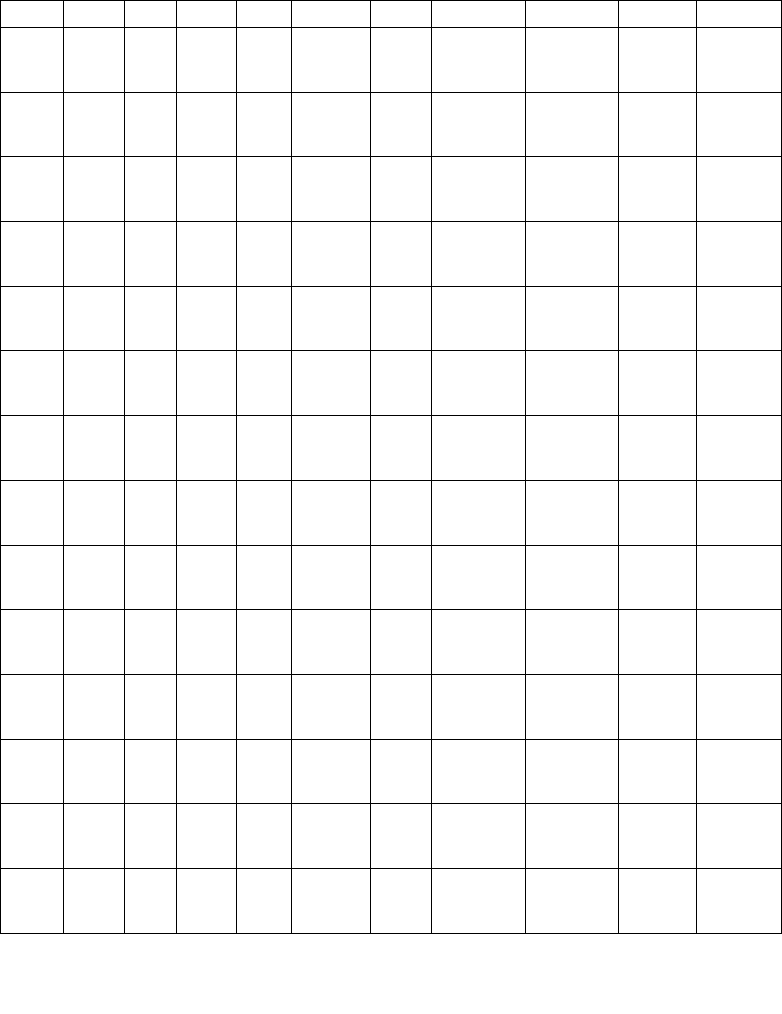
9 0 .2 ,4904 ,178 25
2
0
2 - 0
,5
5 0
,8
0
.25
3
51,563
1
25,391
4
0
2
1
1 4 8 8 2 3 8
,203
5
0,750
1
15
0
2
2
2 - 2
,5
1
0
0
,9
2 1
.736
8
7.5
0
23
2
3
1 4 2 3 1
0
1
.6
0
,755
6
,362
0 8
5
2
4
2 - 4
,5
8 1
0
1
.5
0
.100
5
.039
45
0
2
5
1 2 5 3 1
0
2 0
,0867
0
,65
6
5
0
2
6
2 - 1
,2
1
2
5 0
.6
0
,64
6
,642
0
2
7
1 6 3 9 1 1
.5
0
,864
1
0
0 1
30
2
8
2 - 2
,8
5 1
0
0
.8
0
,452
3
,126
43
0
2
9
1 9 3 6 1 2
.7
7
9,753
4
3,889
5
0
0
3
0
2 - 1
,5
1
0
3 0
.9
0
,563
8
,39
0
2
3
1
1 2 3 5 9 1 0
,0267
0
,321
0 1
00
3
2
2 - 0
,7
5 1
5
0
.3
0
,803
0
,449
4
0
3
3
1 6 1 2 1
0
2 0
,343
0
,0586
1
10
0
Примечание.
0)()0(
22
k
txx
.

Пример конструирования систем ОПУ для ОУ 2-го порядка
1. Математическая модель ОУ.
1.1 Структурная схема ОУ имеет вид
p
1
p
1
)(tu
)(tf
ytx )(
1
)(
2
tx
1.2 Математическая модель ОУ в форме Коши
1
2
21
).(
,
xy
tux
xx
2. Граничные условия
,0
,5
20
10
x
x
.0
,0
21
11
x
x
3. Критерий качества вида
1
0
22
2
2
1
min)54( dtuxxI
Требуется определить. Оптимальное программное управляющее
воздействие
)(tu
, переводящее ОУ из начального состояния:
0;5
1110
xx
в
конечное состояние:
0;0
2120
xx
за интервал времени
секt 1;0
по
оптимальной траектории
)(tx
i
,
2,1i
.
Решение.
Расширенный функционал качества
k
t
t
n
i
iiip
nidttuxfxttuuxxFI
0
,,1min,),,()(),,,,(
1
0
где интегрант расширенного функционала
p
F
, с учетом
0
=1, будет
иметь вид
)()(54
22211
22
2
2
1
uxxxuxxF
p
.
Определение частных производных
p
F
по всем входящим
координатам
2121
,,,,
uxx
:
1
1
1
1
8
xp
px
F
xF
;
2
12
2
2
10
xp
px
F
xF
;
0
2
2
up
pu
F
uF
.
Система уравнений Эйлера – Лагранжа
02
,
,
,010
,08
2
2
21
212
11
u
ux
xx
x
x
или в форме Коши
.10
,8
,5,0
,
122
11
22
21
x
x
x
xx
Для решения системы уравнений Эйлера – Лагранжа, необходимо
определить корни характеристического полинома

.045
1100
008
2
1
00
001
det)det()(
24
pp
p
p
p
p
AEppA
Т.к. корни равны
2;1
4,3,2,1
p
, то общий вид уравнений искомых
экстремалей определяется следующим образом
.22)(
,)(
2
4
2
3212
2
4
2
3211
tttt
tttt
eCeCeCeCtx
eCeCeCeCtx
Постоянные интегрирования
4,1, iC
i
определяются из граничных
условий и соответственно равны:
7025,1;4981,14;3028,7;0984,25
4321
CCCC
.
Уравнение оптимального программного управления
)(tu
определяется
в силу математической модели ОУ с учетом выражений оптимальных
программных траекторий
)(tx
i
,
4,1i
, и имеет вид
tttttttt
eeeeeCeCeCeCtu
222
4
2
321
81,6992,573028,70984,2544)(
.
Временная диаграмма и фазовая траектория процесса управления
представлены на рисунке.
u
0
0,1
5,0
t
1
x
2
x
0
t
0,1
0
t
5,0
0,1
5,0
0
1
x
2
x
0
5
Рис. Временная диаграмма и фазовая траектория процесса управления
Из анализа временной диаграммы следует, что характер процесса
управления апериодический, процесс перехода ОУ из начального состояния
0;5
1110
xx
в конечное состояние
0;0
2120
xx
длится заданный интервал
