Tarek Ahmed. Reservoir engineering handbook
Подождите немного. Документ загружается.


Example 14-6
The linear system in Example 14-5 is under consideration for a water-
flooding project with a water injection rate of 1000 bbl/day. The oil vis-
cosity is considered constant at 1.0 cp. Calculate the fractional flow
curve for the reservoir dip angles of 10, 20, and 30˚, assuming (a) updip
displacement and (b) downdip displacement.
Solution
Step 1. Calculate the density difference (
w
–
o
) in g/cm
3
:
(
w
–
o
) = (64 – 45) / 62.4 = 0.304 g/cm
3
Step 2. Simplify Equation 14-22 by using the given fixed data:
For updip displacement, sin() is positive, therefore:
For downdip displacement, sin() is negative, therefore:
f
k
k
k
w
ro
ro
rw
=
+
()
+
1 0 185
105
. sin
.
α
f
k
k
k
w
ro
ro
rw
=
−
()
+
1 0 185
105
. sin
.
α
f
k
k
k
f
k
k
k
w
ro
ro
rw
w
ro
ro
rw
=
−
()( )
()( )
()()
[]
+
=
−
()
[]
+
1
0 001127 50 25 000
1 1000
0 433 0 304
1
05
1
1 0 185
105
.,
. . sin
.
. sin
.
α
α
898 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:37 Page 898

Step 3. Perform the fractional flow calculations in the following tabulat-
ed form:
f
w
, Updip Displacement f
w
, Downdip Displacement
S
w
k
ro
k
ro
/k
rw
10
o
20
o
30
o
10
o
20
o
30
o
0.24 0.95 00 0 0 0 0 0 0
0.30 0.89 89 0.021 0.021 0.020 0.023 0.023 0.024
0.40 0.74 18.5 0.095 0.093 0.091 0.100 0.102 0.104
0.50 0.45 5.0 0.282 0.278 0.274 0.290 0.294 0.298
0.60 0.19 1.12 0.637 0.633 0.630 0.645 0.649 0.652
0.65 0.12 0.43 0.820 0.817 0.814 0.826 0.830 0.832
0.70 0.06 0.27 0.879 0.878 0.876 0.883 0.884 0.886
0.75 0.03 0.08 0.961 0.960 0.959 0.962 0.963 0.964
0.78 0.00 0 1.000 1.000 1.000 1.000 1.000 1.000
The fractional flow equation, as discussed in the previous section, is
used to determine the water cut f
w
at any point in the reservoir, assuming
that the water saturation at the point is known. The question, however, is
how to determine the water saturation at this particular point. The
answer is to use the frontal advance equation. The frontal advance
equation is designed to determine the water saturation profile in the
reservoir at any give time during water injection.
Frontal Advance Equation
Buckley and Leverett (1942) presented what is recognized as the basic
equation for describing two-phase, immiscible displacement in a linear sys-
tem. The equation is derived based on developing a material balance for the
displacing fluid as it flows through any given element in the porous media:
Volume entering the element – Volume leaving the element
= change in fluid volume
Consider a differential element of porous media, as shown in Figure
14-17, having a differential length dx, an area A, and a porosity φ.
During a differential time period dt, the total volume of water entering
the element is given by:
Volume of water entering the element = q
t
f
w
d
t
The volume of water leaving the element has a differentially smaller
water cut (f
w
– df
w
) and is given by:
Volume of water leaving the element = q
t
(f
w
– df
w
) dt
Principles of Waterflooding 899
Reservoir Eng Hndbk Ch 14 2001-10-25 17:37 Page 899
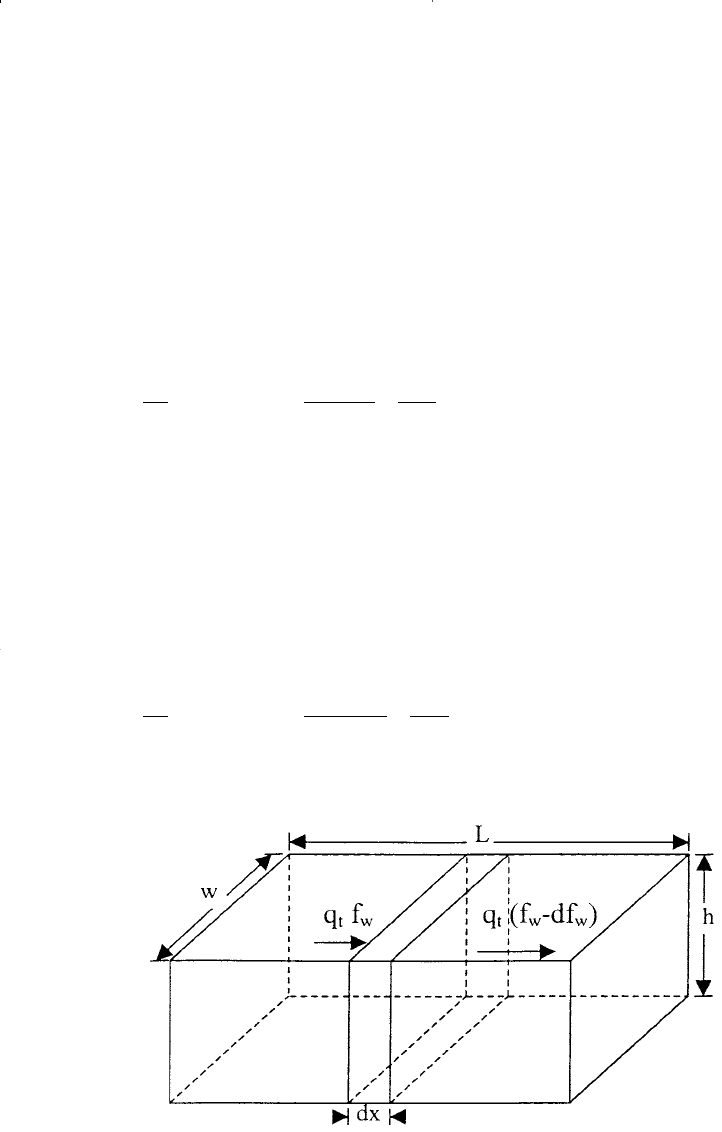
Subtracting the above two expressions gives the accumulation of the
water volume within the element in terms of the differential changes of
the saturation df
w
:
q
t
f
w
d
t
– q
t
(f
w
– df
w
) dt = A (dx) (dS
w
)/5.615
Simplifying:
q
t
df
w
dt = A (dx) (dS
w
)/5.615
Separating the variables gives:
where (υ)
Sw
= velocity of any specified value of S
w
, ft/day
A = cross-sectional area, ft
2
q
t
= total flow rate (oil + water), bbl/day
(df
w
/dS
w
)
Sw
= slope of the f
w
vs. S
w
curve at S
w
The above relationship suggests that the velocity of any specific water
saturation S
w
is directly proportional to the value of the slope of the f
w
vs. S
w
curve, evaluated at S
w
. Note that for two-phase flow, the total flow
rate q
t
is essentially equal to the injection rate i
w
, or:
where i
w
= water injection rate, bbl/day.
Figure 14-17. Water flow through a linear differential element.
dx
dt
i
A
df
dS
Sw
Sw
ww
w
Sw
=
(
)
=
(
)
υ
φ
5 615.
14 - 33
dx
dt
q
A
df
dS
Sw
Sw
tw
w
Sw
=
(
)
=
(
)
υ
φ
5 615.
14 - 32
900 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:37 Page 900

To calculate the total distance any specified water saturation will travel
during a total time t, Equation 14-33 must be integrated:
or
Equation 14-34 can also be expressed in terms of total volume of water
injected by recognizing that under a constant water-injection rate, the
cumulative water injected is given by:
or
where i
w
= water injection rate, bbl/day
W
inj
= cumulative water injected, bbl
t = time, day
(x)
Sw
= distance from the injection for any given saturation S
w
, ft
Equation 14-35 also suggests that the position of any value of water satura-
tion S
w
at given cumulative water injected W
inj
is proportional to the slope
(df
w
/dS
w
) for this particular S
w
. At any given time t, the water saturation pro-
file can be plotted by simply determining the slope of the f
w
curve at each
selected saturation and calculating the position of S
w
from Equation 14-35.
Figure 14-18 shows the typical S shape of the f
w
curve and its derivative
curve. However, a mathematical difficulty arises when using the derivative
curve to construct the water saturation profile at any given time. Suppose
we want to calculate the positions of two different saturations (shown in
Figure 14-18 as saturations A and B) after W
inj
barrels of water have been
injected in the reservoir. Applying Equation 14-35 gives:
x
W
A
df
dt
sw
inj
w
Sw
()
=
()
5 615.
φ
14 - 35
Wti
inj w
=
x
it
A
df
dt
Sw
ww
Sw
()
=
()
5 615.
φ
14 - 34
dx
i
A
df
dt
dt
X
ww
Sw
t
00
5 615
∫∫
=
.
φ
Principles of Waterflooding 901
Reservoir Eng Hndbk Ch 14 2001-10-25 17:37 Page 901
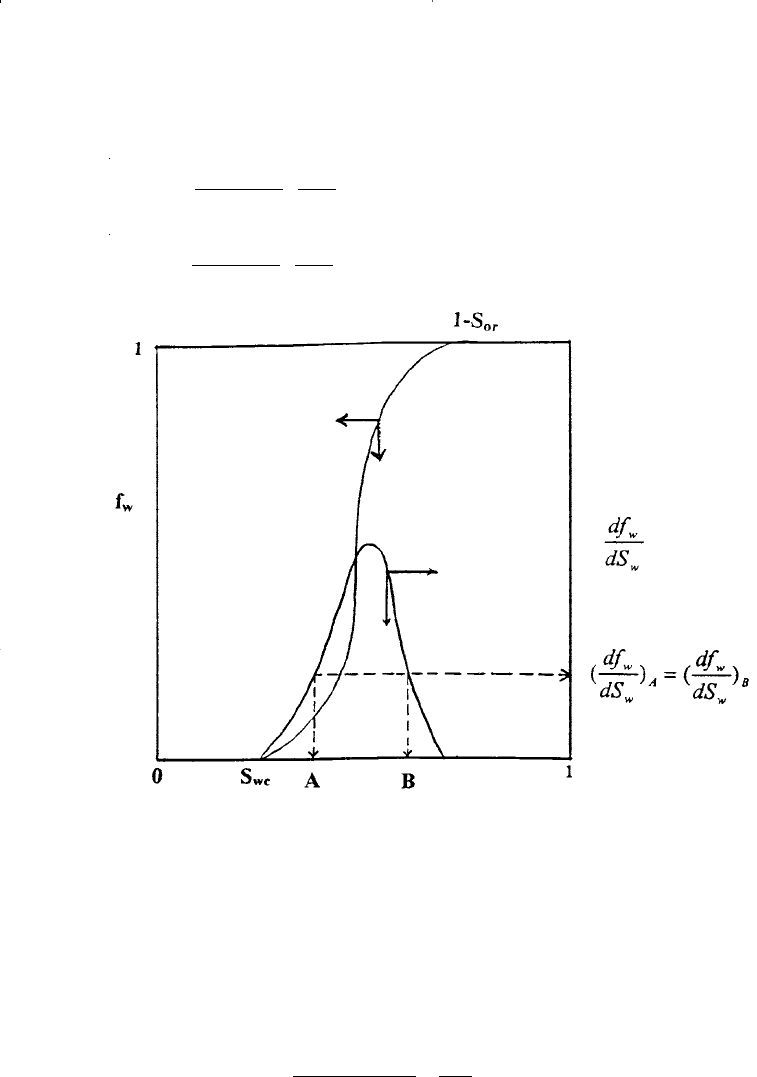
Figure 14-18. The f
w
curve with its saturation derivative curve.
Figure 14-18 indicates that both derivatives are identical, i.e., (df
w
/dS
w
)
A
=
(df
w
/dS
w
)
B
, which implies that multiple water saturations can coexist at the
same position—but this is physically impossible. Buckley and Leverett
(1942) recognized the physical impossibility of such a condition. They point-
ed out that this apparent problem is due to the neglect of the capillary pres-
sure gradient term in the fractional flow equation. This capillary term is
given by:
Including the above capillary term when constructing the fractional flow
curve would produce a graphical relationship that is characterized by the
following two segments of lines, as shown in Figure 14-19:
Capillary term =
0 001127. kA
i
dP
dx
o
ow
c
µ
x
W
A
df
dS
B
inj
w
w
()
=
5 615.
φ
B
x
W
A
df
dS
A
inj
w
w
A
()
=
5 615.
φ
902 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:37 Page 902

• A straight line segment with a constant slope of (df
w
/dS
w
)
Swf
from S
wc
to S
wf
• A concaving curve with decreasing slopes from S
wf
to (1 – S
or
)
Figure 14-19. Effect of the capillary term on the f
w
curve.
Terwilliger et al. (1951) found that at the lower range of water saturations
between S
wc
and S
wf
, all saturations move at the same velocity as a func-
tion of time and distance. Notice that all saturations in that range have
the same value for the slope and, therefore, the same velocity as given by
Equation 14-33:
We can also conclude that all saturations in this particular range will
travel the same distance x at any particular time, as given by Equation
14-34 or 14-35:
x
it
A
df
dS
Sw Swf
ww
w
Swf
(
)
=
<
5 615.
φ
υ
φ
(
)
=
<Sw Swf
ww
w
Swf
i
A
df
dS
5 615.
Principles of Waterflooding 903
Reservoir Eng Hndbk Ch 14 2001-10-25 17:37 Page 903

The result is that the water saturation profile will maintain a constant
shape over the range of saturations between S
wc
and S
wf
with time. Ter-
williger and his coauthors termed the reservoir-flooded zone with this
range of saturations the stabilized zone. They define the stabilized zone
as that particular saturation interval (i.e., S
wc
to S
wf
) where all points of
saturation travel at the same velocity. Figure 14-20 illustrates the concept
of the stabilized zone. The authors also identified another saturation zone
between S
wf
and (1 – S
or
), where the velocity of any water saturation is
variable. They termed this zone the nonstabilized zone.
Figure 14-20. Water saturation profile as a function of distance and time.
Experimental core flood data show that the actual water saturation pro-
file during water flooding is similar to that of Figure 14-20. There is a
distinct front, or shock front, at which the water saturation abruptly
increases from S
wc
to S
wf
. Behind the flood front there is a gradual
increase in saturations from S
wf
up to the maximum value of 1 – S
or
.
Therefore, the saturation S
wf
is called the water saturation at the front or,
alternatively, the water saturation of the stabilized zone.
Welge (1952) showed that by drawing a straight line from S
wc
(or from
S
wi
if it is different from S
wc
) tangent to the fractional flow curve, the
saturation value at the tangent point is equivalent to that at the front S
wf
.
904 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:37 Page 904
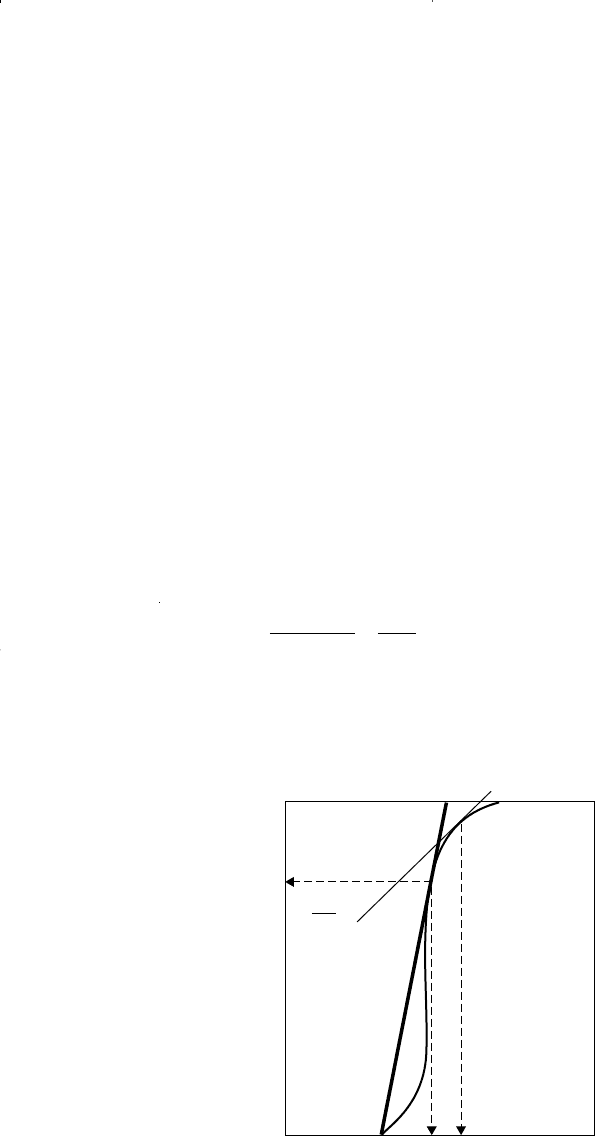
The coordinate of the point of tangency represents also the value of the
water cut at the leading edge of the water front f
wf
.
From the above discussion, the water saturation profile at any given
time t
1
can be easily developed as follows:
Step 1. Ignoring the capillary pressure term, construct the fractional flow
curve, i.e., f
w
vs. S
w
.
Step 2. Draw a straight line tangent from S
wi
to the curve.
Step 3. Identify the point of tangency and read off the values of S
wf
and
f
wf
.
Step 4. Calculate graphically the slope of the tangent as (df
w
/dS
w
)
Swf
.
Step 5. Calculate the distance of the leading edge of the water front from
the injection well by using Equation 14-34, or:
Step 6. Select several values for water saturation S
w
greater than S
wf
and
determine (df
w
/dS
w
)
Sw
by graphically drawing a tangent to the f
w
curve at each selected water saturation (as shown in Figure 14-21).
Figure 14-21. Fractional flow curve.
1
1
0
S
we
S
wf
f
wf
f
w
( )sw
S
w
df
w
dS
w
(df
w
/dS
w
)swf
x
it
A
df
dS
Swf
ww
w
Swf
()
=
5 615
1
.
φ
Principles of Waterflooding 905
Reservoir Eng Hndbk Ch 14 2001-10-25 17:37 Page 905

Step 7. Calculate the distance from the injection well to each selected
saturation by applying Equation 14-36, or:
Step 8. Establish the water saturation profile after t
1
days by plotting
results obtained in step 7.
Step 9. Select a new time t
2
and repeat steps 5 through 7 to generate a
family of water saturation profiles as shown schematically in
Figure 14-20.
Some erratic values of (df
w
/dS
w
)
S
w
might result when determining the
slope graphically at different saturations. A better way is to determine the
derivative mathematically by recognizing that the relative permeability
ratio (k
ro
/k
rw
) can be expressed by Equation 5-29 of Chapter 5 as:
Notice that the slope b in the above expression has a negative value. The
above expression can be substituted into Equation 14-26 to give:
The derivative of (df
w
/dS
w
)
S
w
may be obtained mathematically by differ-
entiating the above equation with respect to S
w
to give:
df
dS
abe
ae
w
w
Sw
w
o
bS
w
o
bS
w
w
=
−
+
(
)
µ
µ
µ
µ
14 - 38
1
2
f
ae
w
w
o
bS
w
=
+
(
)
1
1
µ
µ
14 - 37
k
k
ae
ro
rw
bS
w
=
(
)
14 - 36
x
it
A
df
dS
Sw
ww
w
S
w
(
)
=
5 615
1
.
φ
906 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 14 2001-10-25 17:37 Page 906

The data in the following example, as given by Craft and Hawkins
(1959), are used to illustrate one of the practical applications of the
frontal displacement theory.
Example 14-7
The following data are available for a linear-reservoir system:
S
w
0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75
k
ro
/k
rw
30.23 17.00 9.56 5.38 3.02 1.70 0.96 0.54 0.30 0.17 0.10
Oil formation volume factor B
o
= 1.25 bbl/STB
Water formation volume factor B
w
= 1.02 bbl/STB
Formation thickness h = 20 ft
Cross-sectional area A = 26,400 ft
Porosity = 25%
Injection rate i
w
= 900 bbl/day
Distance between producer and injector L = 600 ft
Oil viscosity
o
= 2.0 cp
Water viscosity
w
= 1.0 cp
Dip angle = 0°
Connate water saturation S
wc
= 20%
Initial water saturation S
wi
= 20%
Residual water saturation S
or
= 20%
Calculate and plot the water saturation profile after 60, 120, and 240
days.
Solution
Step 1. Plot the relative permeability ratio k
ro
/k
rw
vs. water saturation on
a semi-log paper and determine the coefficients a and b of Equa-
tion 14-36, as shown in Figure 14-22, to give:
Therefore,
k
k
e
ro
rw
S
w
=
−
537 59
11 51
.
.
ab==−537 59 11 51.. and
Principles of Waterflooding 907
Reservoir Eng Hndbk Ch 14 2001-10-25 17:37 Page 907
