Tarek Ahmed. Reservoir engineering handbook
Подождите немного. Документ загружается.


The following additional data are available:
p
i
= p
b
= 4350 psi S
wi
= 30% N = 15 MMSTB
Predict the cumulative oil and gas production to 3350 psi.
Solution
A sample of the Tracy’s calculation procedure is performed at 4150 psi.
Step 1. Calculate Tracy’s PVT functions at 4150
• Calculate the term Den from Equation 12-37
Den = (B
o
− B
oi
) + (R
si
− R
s
) B
g
Den = (1.42 − 1.43) + (840 − 820) (7.1 × 10
−4
) = 0.0042
• Calculate Φ
o
and Φ
g
Φ
o
= (B
o
− R
s
B
g
)/Den
Φ
o
= [1.42 − (820) (7.1 × 10
−4
)]/0.0042 = 199
Φ
g
= B
g
/Den
= 7.1 × 10
−4
/0.0042 = 0.17
Similarly, these PVT variables are calculated for all other pres-
sures to give:
p Φ
o
Φ
g
4350 — —
4150 199 0.17
3950 49 0.044
3750 22.6 0.022
3550 13.6 0.014
3350 9.42 0.010
808 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 12 2001-10-25 16:04 Page 808

Step 2. Assume a value for the GOR at 4150 psi as 850 scf/STB.
Step 3. Calculate the average GOR.
Step 4. Calculate the incremental cumulative oil production ∆N
p
.
Step 5. Calculate the cumulative oil production N
p
.
N
p
= N
*
p
+∆N
p
N
p
= 0 + 0.00292 = 0.00292
Step 6. Calculate oil and gas saturations.
S
o
= (1 − N
p
) (B
o
/B
oi
) (1 − S
wi
)
S
o
= (1 − 0.00292) (1.42/1.43) (1 − 0.3) = 0.693
S
g
= 1 − S
wi
− S
o
S
g
= 1 − 0.3 − 0.693 = 0.007
Step 7. Determine the relative permeability ratio k
rg
/k
ro
from Figure 12-7,
to give:
k
rg
/k
ro
= 8 × 10
−5
Step 8. Using µ
o
= 1.7 cp and µ
g
= 0.023 cp, calculate the instantaneous
GOR.
which agrees with the assumed value.
GOR = 820 + (1.7 ×
×
=
−
−
10
17 142
0 023 7 1 10
845
4
4
)
(.)(. )
(. )(. )
/scf STB
∆N STB
p
=
−
+
(
)
(
)
=
10
199 845 0 17
0 00292
.
.
GOR scf STB
avg
(
)
=
+
=
840 850
2
845 /
Predicting Oil Reservoir Performance 809
Reservoir Eng Hndbk Ch 12 2001-10-25 16:04 Page 809

Step 9. Calculate cumulative gas production.
G
p
= 0 + (0.00292) (850) = 2.48
Complete results of the method are shown below:
G
p
N
p
= 15 × 10
6
NG
p
= 15 × 10
6
N
p
–
∆N
p
N
p
(GOR)
avg
∆G
p
scf/STB STB scf
4350 — — — — — — —
4150 0.00292 0.00292 845 2.48 2.48 0.0438 × 10
6
37.2 × 10
6
3950 0.00841 0.0110 880 7.23 9.71 0.165 × 10
6
145.65 × 10
6
3750 0.0120 0.0230 1000 12 21.71 0.180 × 10
6
325.65 × 10
6
3550 0.0126 0.0356 1280 16.1 37.81 0.534 × 10
6
567.15 × 10
6
3350 0.011 0.0460 1650 18.2 56.01 0.699 × 10
6
840 × 10
6
Muskat’s Method
Muskat (1945) expressed the material balance equation for a deple-
tion-drive reservoir in the following differential form:
with
∆S
o
= S
*
o
− S
o
∆p = p
*
− p
where S
*
o
, p
*
= oil saturation and average reservoir pressure at the
beginning of the pressure step
S
o
, p = oil saturation and average reservoir pressure at the end
of the time step
R
s
= gas solubility, scf/STB
B
g
= gas formation volume factor, bbl/scf
Craft, Hawkins, and Terry (1991) suggested the calculations can be
greatly facilitated by computing and preparing in advance in graphical
form the following pressure dependent groups:
dS
dp
SB
B
dR
dp
S
B
k
k
dB
dp
SSB
dB
dp
k
k
o
og
o
so
o
rg
ro
o
g
o
owcg
g
o
g
rg
ro
=
++−−
+
µ
µ
µ
µ
()
(/ )
1
1
1
(12 - 45)
810 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 12 2001-10-25 16:04 Page 810

Introducing the above pressure dependent terms into Equation 12-45,
gives:
Craft, Hawkins, and Terry (1991) proposed the following procedure for
solving Muskat’s equation for a given pressure drop ∆p, i.e., (p* − p):
Step 1. Prepare a plot of k
rg
/k
ro
versus gas saturation.
Step 2. Plot R
s
, B
o
and (1/B
g
) versus pressure and determine the slope of
each plot at selected pressures, i.e., dB
o
/dp, dR
s
/dp, and d(1/B
g
)/dp.
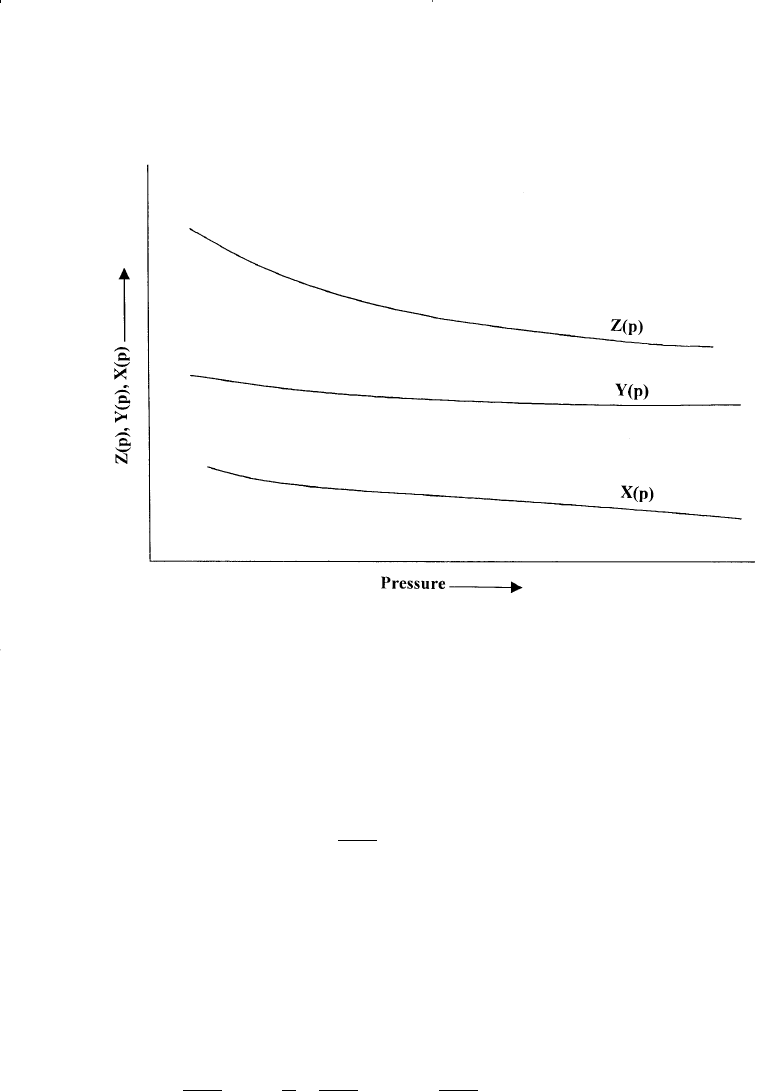
Step 3. Calculate the pressure dependent terms X(p), Y(p), and Z(p) that
correspond to the selected pressures in Step 2.
Step 4. Plot the pressure dependent terms as a function of pressure, as
illustrated in Figure 12-8.
Step 5. Graphically determine the values of X(p), Y(p), and Z(p) that cor-
respond to the pressure p.
Step 6. Solve Equation 12-49 for (∆S
o
/∆p) by using the oil saturation S
*
o
at the beginning of the pressure drop interval p*.
∆
∆
S
p
SXp S
k
k
Yp S S Zp
k
k
o
oo
rg
ro
owc
o
g
rg
ro
=
++−−
+
() () ( ) ()1
1
µ
µ
(12 - 49)
Zp B
dB
dp
g
g
()
(/ )
=
1
(12 - 48)
Yp
B
dB
dp
o
o
g
o
()=
1
µ
µ
(12 - 47)
Xp
B
B
dR
dp
g
o
s
()= (12 - 46)
Predicting Oil Reservoir Performance 811
Reservoir Eng Hndbk Ch 12 2001-10-25 16:04 Page 811
Step 7. Determine the oil saturation S
o
at the average reservoir pressure
p, from:
Step 8. Using the S
o
from Step 7 and the pressure p, recalculate (∆S
o
/∆p)
from Equation 12-49.
Step 9. Calculate the average value for (∆S
o
/∆p) from the two values
obtained in Steps 6 and 8, or:
∆
∆
∆
∆
∆
∆
S
p
S
p
S
p
o
avg
o
step
o
step
=
+
1
2
68
SS pp
S
p
oo
o
=− −
∗
()
*
∆
∆
(12 - 50)
812 Reservoir Engineering Handbook
Figure 12-8. Pressure dependant terms vs. p.
Reservoir Eng Hndbk Ch 12 2001-10-25 16:04 Page 812

Step 10. Using (∆S
o
/∆p)
avg
, solve for the oil saturation S
o
from:
This value of S
o
becomes S
*
o
for the next pressure drop interval.
Step 11. Calculate gas saturation S
g
by:
S
g
= 1 − S
wi
− S
o
Step 12. Using the saturation equation, i.e., Equation 12-15, solve for the
cumulative oil production.
Step 13. Calculate the cumulative gas production by using Equations 12-40
and 12-41.
Step 14. Repeat Steps 5 through 13 for all pressure drops of interest.
Example 12-5
2
A volumetric depletion-drive reservoir exists at its bubble-point pres-
sure of 2500 psi. Detailed fluid property data are listed by Craft and his
coauthors and given here at only two pressures.
Fluid property p
b
= 2500 psi p = 2300 psi
B
o
, bbl/STB 1.498 1.463
R
s
, scf/STB 721 669
B
g
, bbl/scf 0.001048 0.001155
µ
o
, cp 0.488 0.539
µ
g
, cp 0.0170 0.0166
X (p) 0.00018 0.00021
Y (p) 0.00328 0.00380
Z (p) 0.00045 0.00050
NN
B
B
S
S
P
oi
o
o
wi
=−
−
1
1
(12 - 52)
SS pp
S
p
oo
o
avg
=− −
∗
()
*
∆
∆
(12 - 51)
Predicting Oil Reservoir Performance 813
2
Craft, B. C., Hawkins, M., Terry, R., Applied Petroleum Reservoir Engineering, 2nd ed.
Prentice Hall, 1991.
Reservoir Eng Hndbk Ch 12 2001-10-25 16:04 Page 813

The following additional information is available:
N = 56 MMSTB S
wi
= 20% S
oi
= 80%
S
g
k
rg
/k
ro
0.10 0.010
0.20 0.065
0.30 0.200
0.50 2.000
0.55 3.000
0.57 5.000
Calculate the cumulative oil production for a pressure drop of 200 psi,
i.e., at 2300 psi.
Solution
Step 1. Using the oil saturation at the beginning of the pressure interval,
i.e., S
*
o
= 0.8, calculate (k
rg
/k
ro
) to give:
k
rg
/k
ro
= 0.0 (No free gas initially in place.)
Step 2. Evaluate (∆S
o
/∆p) by applying Equation 12-49.
Step 3. Estimate the oil saturation at p = 2300 psi from Equation 12-51.
S
o
= 0.8 − 200 (0.000146) = 0.7709
Step 4. Recalculate (∆S
o
/∆p) by using S
o
= 0.7709 and the pressure
dependent terms at 2300 psi.
∆
∆
∆
∆
S
p
o
S
p
o
=
++−−
+
=
0 7709 0 00021 0 7709 0 00001 0 0038 1 0 2 0 7709 0 0005
1
0 539
0 0166
0 00001
0 000173
.(. ).(. ). (..).
.
.
(. )
.
∆
∆
S
p
o
=
++
+
=
(.)(. )
.
0 8 0 00018 0 0
10
0 000146
814 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 12 2001-10-25 16:04 Page 814

Step 5. Calculate the average (∆S
o
/∆p).
Step 6. Calculate S
o
= 0.8 − (2500 − 2300) (0.000159) = 0.7682.
Step 7. Calculate gas saturation.
S
g
= 1 − 0.2 − 0.7682 + 0.0318
Step 8. Calculate cumulative oil production at 2300 psi by using Equa-
tion 12-52.
Step 9. Calculate k
rg
/k
ro
at 2300 psi, to give k
rg
/k
ro
= 0.00001.
Step 10. Calculate the instantaneous GOR at 2300 psi.
Step 11. Calculate cumulative gas production.
It should be stressed that this method is based on the assumption of
uniform oil saturation in the whole reservoir and that the solution will
therefore break down when there is appreciable gas segregation in the
formation. It is therefore applicable only when permeabilities are rela-
tively low.
Tarner’s Method
Tarner (1944) suggests an iterative technique for predicting cumulative
oil production N
p
and cumulative gas production G
p
as a function of
G MMscf
p
=
+
=
669 669
2
939 500 629,
GOR scf STB=+ =669 0 00001
0 539 1 463
0 0166 0 001155
669.
(. )(. )
(. )(. )
/
N STB
p
=× −
−
=56 10 1
1 498
1 463
0 7682
102
939 500
6
.
.
.
.
,
∆
∆
S
p
o
avg
=
+
=
0 000146 0 000173
2
0 000159
..
.
Predicting Oil Reservoir Performance 815
Reservoir Eng Hndbk Ch 12 2001-10-25 16:04 Page 815

reservoir pressure. The method is based on solving the material-balance
equation and the instantaneous gas-oil ratio equation simultaneously for
a given reservoir pressure drop from p
1
to p
2
. It is accordingly assumed
that the cumulative oil and gas production has increased from N
p1
and
G
p1
to N
p2
and G
p2
. To simplify the description of the proposed iterative
procedure, the stepwise calculation is illustrated for a volumetric saturat-
ed-oil reservoir. It should be pointed out that Tarner’s method could be
extended to predict the volumetric behavior of reservoirs under different
driving mechanisms.
Step 1. Select a future reservoir pressure p
2
below the initial (current)
reservoir pressure p
1
and obtain the necessary PVT data. Assume
that the cumulative oil production has increased from N
p1
to N
p2
.
It should be pointed out that N
p1
and G
p1
are set equal to zero at
the initial reservoir pressure, i.e., bubble-point pressure.
Step 2. Estimate or guess the cumulative oil production N
p2
at p
2
.
Step 3. Calculate the cumulative gas production G
p2
by rearranging the
MBE, i.e., Equation 12-33, to give:
Equivalently, the above relationship can be expressed in terms
of the two-phase (total) formation volume factor B
t
as:
where B
g
= gas formation volume factor at p
2
, bbl/scf
B
o
= oil formation volume factor at p
2
, bbl/STB
B
t
= two-phase formation volume factor at p
2
, bbl/STB
N = initial oil in place, STB
Step 4. Calculate the oil and gas saturations at the assumed cumulative
oil production N
p2
and the selected reservoir pressure p
2
by apply-
ing Equations 12-15 and 12-16 respectively, or:
G
NB B N B R B
B
p
tti ptsig
g
2
2
=
−− −()( )
(12 - 54)
GNRR
BB
N
B
B
R
psis
oi o
p
o
g
s22
=−−
−
−−
()
B
(12 - 53)
g
816 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 12 2001-10-25 16:04 Page 816

where B
o
= initial oil formation volume factor at p
i
, bbl/STB
B
o
= oil formation volume factor at p
2
, bbl/STB
S
g
= gas saturation at p
2
B
o
= oil saturation at p
2
Step 5. Using the available relative permeability data, determine the rela-
tive permeability ratio k
rg
/k
ro
that corresponds to the gas satura-
tion at p
2
and compute the instantaneous (GOR)
2
at p
2
from Equa-
tion 12-1, as:
It should be noted that all the PVT data in the expression must be
evaluated at the assumed reservoir pressure p
2
.
Step 6. Calculate again the cumulative gas production G
p2
at p
2
by apply-
ing Equation 12-7, or:
in which (GOR)
1
represents the instantaneous GOR at p
1
. If p
1
represents the initial reservoir pressure, then set (GOR)
1
= R
si
.
Step 7. The total gas produced G
p2
during the first prediction period as
calculated by the material balance equation is compared to the
total gas produced as calculated by the GOR equation. These two
equations provide with two independent methods required for
determining the total gas produced. Therefore, if the cumulative
gas production G
p2
as calculated from Step 3 agrees with the
value of Step 6, the assumed value of N
p2
is correct and a new
GG
GOR GOR
NN
pp pp21
12
21
2
=+
+
−()
()()
[ ] (12 - 56)
()GOR R
k
k
B
B
s
rg
ro
oo
gg
2
=+
µ
µ
(12 - 55)
SS
N
N
B
B
SSS
owi
p
o
oi
gowi
=− −
=− −
()11
1
2
Predicting Oil Reservoir Performance 817
Reservoir Eng Hndbk Ch 12 2001-10-25 16:04 Page 817
