Tarek Ahmed. Reservoir engineering handbook

Подождите немного. Документ загружается.

Example 9-5

A vertical well is drilled on a regular 40-acre spacing in an oil reser-

voir that is overlaid by a gas cap and underlaid by an aquifer. The follow-

ing data are available:

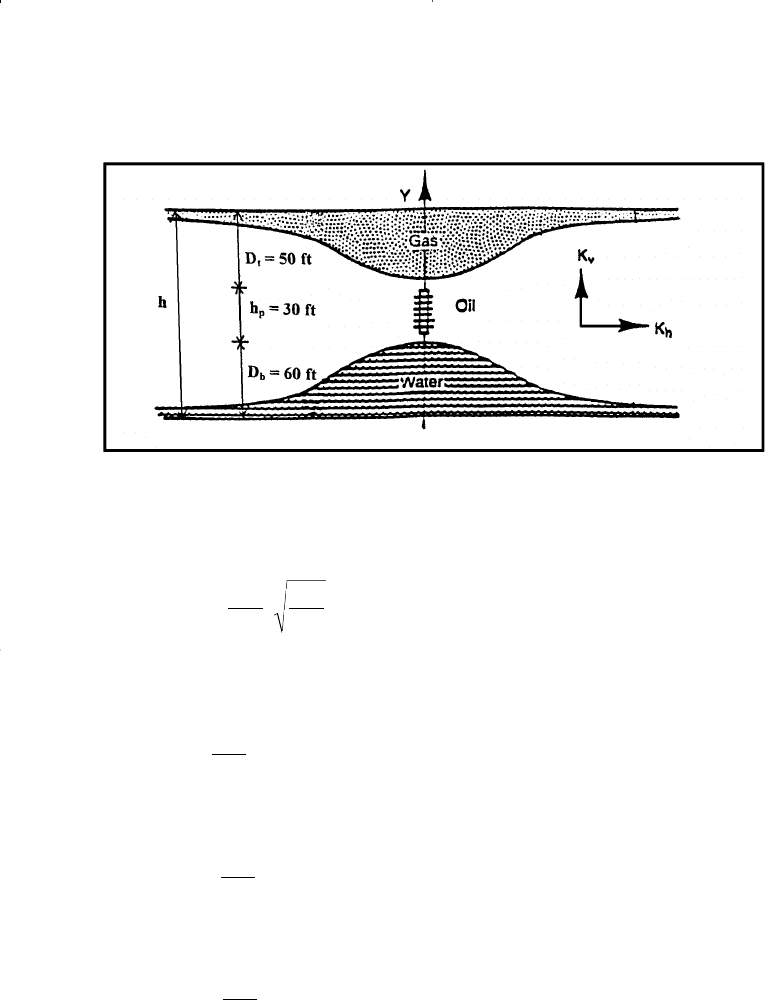
Oil pay thickness h = 140 ft

Distance from the GOC to the top of perforations D

= 50 ft

Length of the perforated interval h

= 30 ft

Horizontal permeability k

= 300 md

Relative oil permeability k

= 1.00

Vertical permeability k

= 90 md

Oil density r

= 46.24 lb/ft

Water density r

= 68.14 lb/ft

Gas density r

= 6.12 lb/ft

Oil FVF B

= 1.25 bbl/STB

Oil viscosity m

= 1.11 cp

A schematic representation of the given data is shown in Figure 9-15.

Calculate the maximum allowable oil-flow rate without water and

free-gas production.

Solution

Step 1. Calculate the drainage radius r

= (40)(43,560)

= 745 ft

Step 2. Compute the distance from the WOC to the bottom of the perfo-

rations D

= h - D

- h

= 140 - 50 - 30 = 60 ft

588 Reservoir Engineering Handbook

(text continued from page 584)

Reservoir Eng Hndbk Ch 09 2001-10-25 08:37 Page 588

Step 3. Find the dimensionless radius r

from Equation 9-5:

Step 4. Calculate the dimensionless perforated length e by applying

Equation 9-6:

Step 5. Calculate the gas cone ratio d

from Equation 9-7:

Step 6. Determine the water cone ratio d

by applying Equation 9-8:

Step 7. Calculate the oil-gas and water-oil density differences:

- r

= 68.14 - 46.24 = 21.90 lb/ft

- r

= 46.24 - 6.12 = 40.12 lb/ft

140

= 0.429

140

= 0.357

e =

140

= 0.214

745

140

300

= 9.72

Gas and Water Coning 589

Figure 9-15. Gas and water coning problem (Example 9-5).

Reservoir Eng Hndbk Ch 09 2001-10-25 08:37 Page 589

Step 8. Find the density differences ratio:

Step 9. From Figure 9-10, which corresponds to r

= 10; approximate

the dimensionless functions y

and y

for e=0.214 and d

= 0.357 to give y

= 0.051

and

for e=0.214 and d

= 0.429 to give y

= 0.065

Step 10. Estimate the oil critical rate by applying Equations 9-9 and 9-10:

These calculations show that the water coning is the limiting condition

for the oil-flow rate. The maximum oil rate without water or free-gas

production is, therefore, 297 STB/day.

Chierici and Ciucci (1964) proposed a methodology for determining

the optimum completion interval in coning problems. The method is

basically based on the “trial and error” approach.

For a given dimensionless radius r

and knowing GOC, WOC, and

fluids density, the specific steps of the proposed methodology are sum-

marized below:

Step 1. Assume the length of the perforated interval h

Step 2. Calculate the dimensionless perforated length e=h

/h.

Step 3. Select the appropriate family of curves that corresponds to r

interpolate if necessary, and enter the working charts with e on

the x-axis and move vertically to the calculated ratio Dr

/Dr

= 0.492

140

(21.90)

(1.25) (1.11)

(1) (300) STB day

= 0.492

140

(40.12)

(1.25) (1.11)

(1) (300) 0.051 = 426 STB/day

¥=

10 0 065 97

[]. /

[]

og ow

40.12

21.90

= 1.83

590 Reservoir Engineering Handbook

Reservoir Eng Hndbk Ch 09 2001-10-25 08:37 Page 590

Estimate the corresponding d and y. Designate these two dimen-

sionless parameters as the optimum gas cone ratio d

g,opt

and opti-

mum dimensionless function y

opt

Step 4. Calculate the distance from GOC to the top of the perforation,

= (h) (d

g,opt

)

Step 5. Calculate the distance from the WOC to the bottom of the perfo-

ration, h

= h - D

- h

Step 6. Using the optimum dimensionless function y

opt

in Equation 9-9;

calculate the maximum allowable oil-flow rate Q

Step 7. Repeat Steps 1 through 6.

Step 8. The calculated values of Q

at different assumed perforated

intervals should be compared with those obtained from flow-rate

equations, e.g., Darcy’s equation, using the maximum drawdown

pressure.

Example 9-6

Example 9-5 indicates that a vertical well is drilled in an oil reservoir

that is overlaid by a gas cap and underlaid by an aquifer. Assuming that

the pay thickness h is 200 feet and the rock and fluid properties are iden-

tical to those given in Example 9-5, calculate length and position of the

perforated interval.

Solution

Step 1. Using the available data, calculate

745

200

300

= 6.8

and

/ = 40.12 / 21.90 = 1.83

og wo

Gas and Water Coning 591

Reservoir Eng Hndbk Ch 09 2001-10-25 08:37 Page 591

Step 2. Assume the length of the perforated interval is 40 feet; therefore,

= 40¢

e=40/200 = 0.2

Step 3. To obtain the values of y

opt

and d

g,opt

for r

= 6.8, interpolate

between Figures 9-8 and 9-9 to give

opt

= 0.043

g,opt

= 0.317

Step 4. Calculate the distance from GOC to the top of the perforations.

= (200) (0.317) = 63 ft

Step 5. Determine the distance from the WOC to the bottom of the perfo-

rations.

= 200 - 63 - 40 = 97 ft

Step 6. Calculate the optimum oil-flow rate.

Step 7. Repeat Steps 2 through 6 with the results of the calculation as

shown below. The oil-flow rates as calculated from appropriate

flow equations are also included.

20 40 60 80 100

e 0.1 0.2 0.3 0.4 0.5

opt

0.0455 0.0430 0.0388 0.0368 0.0300

g,opt

0.358 0.317 0.271 0.230 0.190

72 63 54 46 38

108 97 86 74 62

)

opt

786 740 669 600 516

Expected Q

525 890 1320 1540 1850

opt

(

)

= 0.492

200

( ) (300) (0.043)

(1.25) (1.11)

= 740 STB/day

40 12

592 Reservoir Engineering Handbook

Reservoir Eng Hndbk Ch 09 2001-10-25 08:37 Page 592

The maximum oil production rate that can be obtained from this

well without coning breakthrough is 740 STB/day. This indicates

that the optimum distance from the GOC to the top of the perfora-

tions is 63 ft and the optimum distance from the WOC to the bot-

tom of the perforations is 97 ft. The total length of the perforated

interval is 200 - 63 - 97 = 40 ft.

The Hoyland-Papatzacos-Skjaeveland Methods

Hoyland, Papatzacos, and Skjaeveland (1989) presented two methods

for predicting critical oil rate for bottom water coning in anisotropic,

homogeneous formations with the well completed from the top of the

formation. The first method is an analytical solution, and the second is a

numerical solution to the coning problem. A brief description of the

methods and their applications are presented below.

The Analytical Solution Method

The authors presented an analytical solution that is based on the

Muskat-Wyckoff (1953) theory. In a steady-state flow condition, the

solution takes a simple form when it is combined with the method of

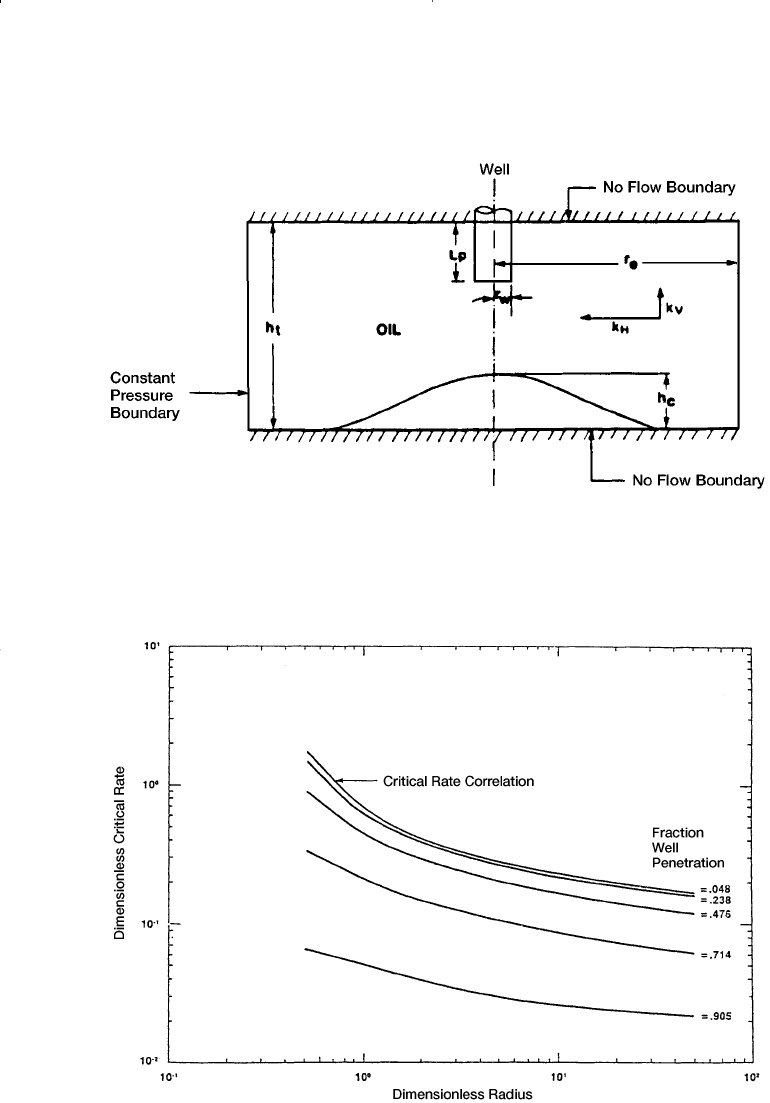
images to give the boundary conditions as shown in Figure 9-16.

To predict the critical rate, the authors superimpose the same criteria

as those of Muskat and Wyckoff on the single-phase solution and, there-

fore, neglect the influence of cone shape on the potential distribution.

Hoyland and his coworkers presented their analytical solution in the fol-

lowing form:

where Q

= critical oil rate, STB/day

h = total thickness of the oil zone, ft

, r

= water and oil density, lb/ft

= horizontal permeability, md

= dimensionless critical flow rate

The authors correlated the dimensionless critical rate q

with the

dimensionless radius r

and the fractional well penetration ratio h

/h as

shown in Figure 9-17.

= 0.246

()

q¥

(9 -11)

Gas and Water Coning 593

Reservoir Eng Hndbk Ch 09 2001-10-25 08:37 Page 593

594 Reservoir Engineering Handbook

Figure 9-16. Illustration of the boundary condition for analytical solution. (After

Hoyland, A. et al., courtesy SPE Reservoir Engineering, November 1989.)

Figure 9-17. Critical rate correlation. (After Hoyland, A. et al., courtesy SPE Reser-

voir Engineering, November 1989.)

Reservoir Eng Hndbk Ch 09 2001-10-25 08:37 Page 594

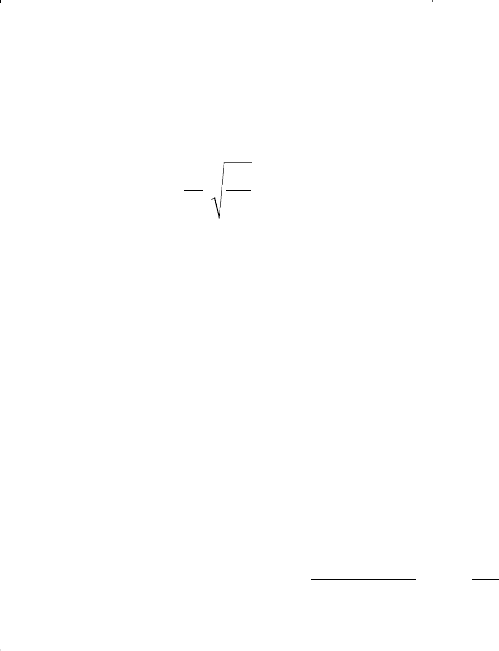
where r

= drainage radius, ft

= vertical permeability, md

= horizontal permeability, md

The Numerical Solution Method

Based on a large number of simulation runs with more than 50 critical

rate values, the authors used a regression analysis routine to develop the

following relationships:

• For isotropic reservoirs with k

= k

, the following expression is pro-

posed:

• For anisotropic reservoirs, the authors correlated the dimensionless crit-

ical rate with the dimensionless radius r

and five different fractional

well penetrations. The correlation is presented in a graphical form as

shown in Figure 9-18.

The authors illustrated their methodology through the following example.

Example 9-7

Given the following data, determine the oil critical rate:

Density differences (water/oil), lbm/ft

= 17.4

Oil FVF, RB/STB = 1.376

Oil viscosity, cp = 0.8257

Horizontal permeability, md = 1,000

Vertical permeability, md = 640

Total oil thickness, ft = 200

Perforated thickness, ft = 50

External radius, ft = 500

2.238

1.99

= 0.924

()

l (

)

1 325

[n ]

(9 -13)

(9 -12)

Gas and Water Coning 595

Reservoir Eng Hndbk Ch 09 2001-10-25 08:37 Page 595

Solution

Step 1. Calculate the dimensionless radius r

by applying Equation 9-12.

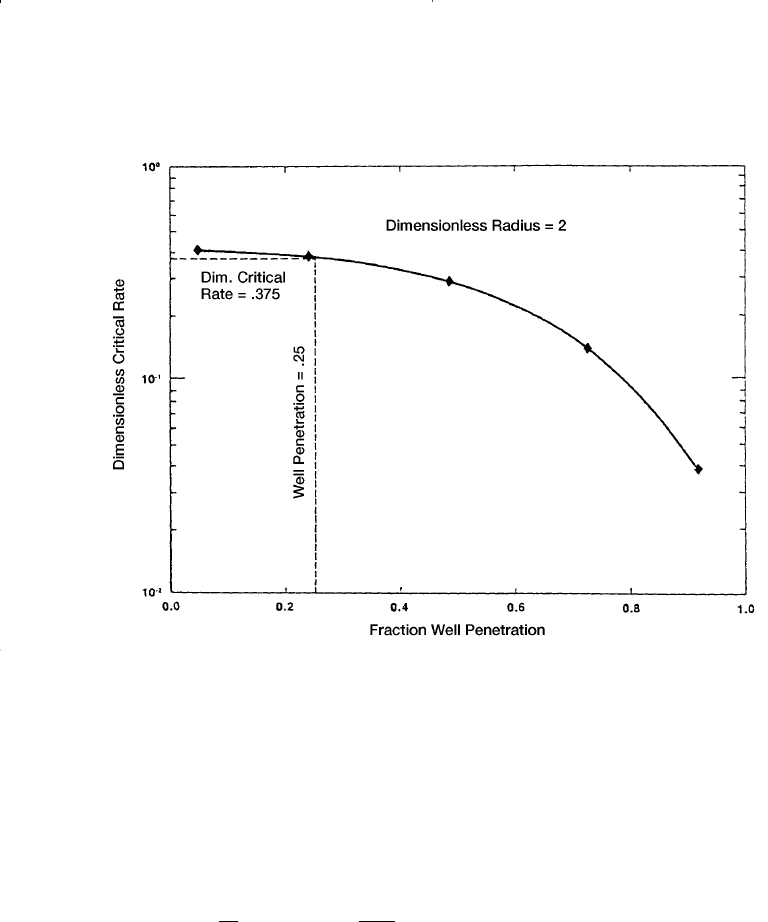
Step 2. Determine dimensionless critical rate for several fractional well

penetrations from Figure 9-17 for a dimensionless radius of 2.

Step 3. Plot dimensionless critical rate as a function of well penetration.

The plot is shown in section A of Figure 9-17.

Step 4. Calculate fractional well penetration, h

/h = 50/200 = 0.25.

(/) (/ )

..05 05

500

200

40 1000 2==

596 Reservoir Engineering Handbook

Figure 9-18. Critical rate calculation for Example 9-7. (After Hoyland, A. et al.,

courtesy SPE Reservoir Engineering, November 1989.)

Reservoir Eng Hndbk Ch 09 2001-10-25 08:37 Page 596

Step 5. Interpolate in the plot in section A of Figure 9-17 to find dimen-

sionless critical rate q

equal to 0.375.

Step 6. Use Equation 9-11 and find the critical rate.

Critical Rate Curves by Chaney et al.

Chaney et al. (1956) developed a set of working curves for determin-

ing oil critical flow rate. The authors proposed a set of working graphs

that were generated by using a potentiometric analyzer study and apply-

ing the water coning mathematical theory as developed by Muskat-

Wyckoff (1935).

The graphs, as shown in Figures 9-19 through 9-23, were generated

using the following fluid and sand characteristics:

Drainage radius r

= 1000 ft

Wellbore radius r

= 3≤

Oil column thickness h = 12.5, 25, 50, 75 and 100 ft

Permeability k = 1000 md

Oil viscosity m

= 1 cp

-r

= 18.72 lb/ft

-r

= 37.44 lb/ft

The graphs are designed to determine the critical flow rate in oil-water,

gas-oil, and gas-water systems with fluid and rock properties as listed

above. The hypothetical rates as determined from the Chaney et al. curves

(designated as Q

curve

), are corrected to account for the actual reservoir rock

and fluid properties by applying the following expressions:

In oil-water systems

curve

= 0.5288

()

(9 -14)

STB day

0 246 10

200 17 4

1 376 0 8257

1000 0 375

5 651

(.)

(. )(. )

()(.)

Gas and Water Coning 597

(text continued on page 603)

Reservoir Eng Hndbk Ch 09 2001-10-25 08:37 Page 597