Tarek Ahmed. Reservoir engineering handbook
Подождите немного. Документ загружается.

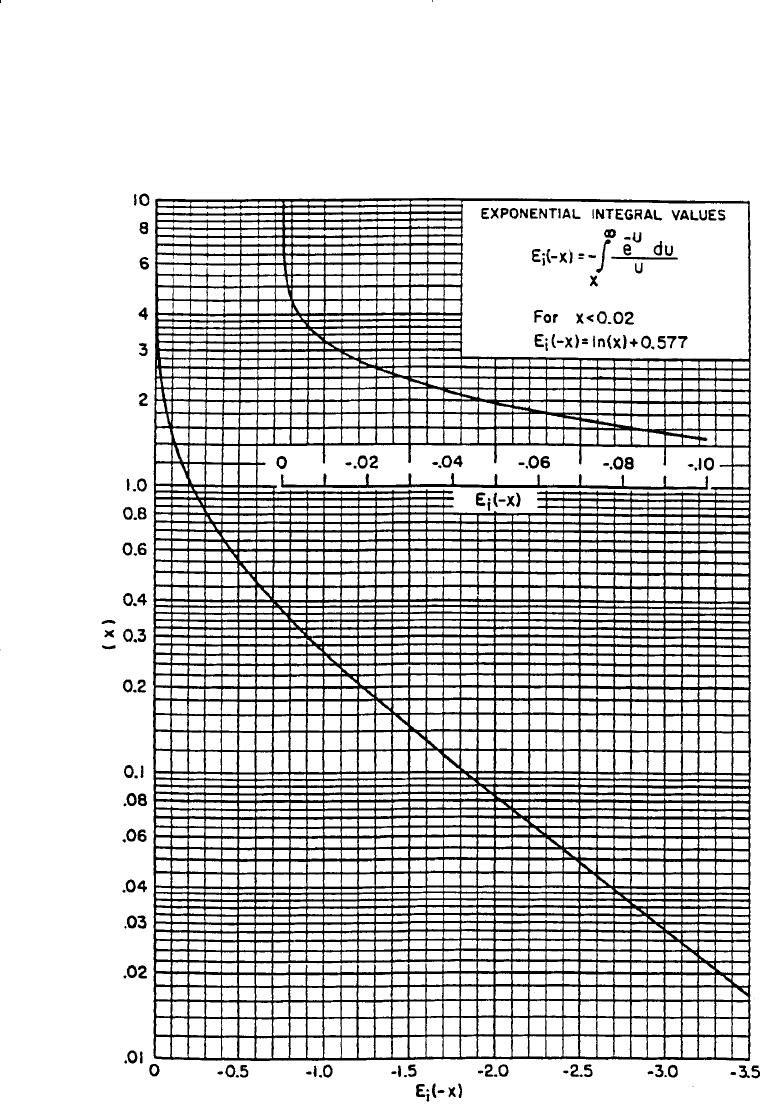
378 Reservoir Engineering Handbook
Figure 6-19. The E
i
-function. (After Craft, Hawkins, and Terry, 1991.)
Reservoir Eng Hndbk Ch 06a 2001-10-25 11:23 Page 378

1. Calculate pressure at radii of 0.25, 5, 10, 50, 100, 500, 1000, 1500,
2000, and 2500 feet, for 1 hour.
Plot the results as:
a. Pressure versus logarithm of radius
b. Pressure versus radius
2. Repeat part 1 for t = 12 hours and 24 hours. Plot the results as pressure
versus logarithm of radius.
Solution
Step 1. From Equation 6-78:
Step 2. Perform the required calculations after one hour in the following
tabulated form:
Elapsed Time t = 1 hr
r, ft x = −42.6(10
−6
)E
i
(−x) p(r,1) = 4000 + 44.125 E
i
(−x)
0.25 −2.6625(10
−6
) −12.26* 3459
5 −0.001065 −6.27* 3723
10 −0.00426 −4.88* 3785
50 −0.1065 −1.76
†
3922
100 −0.4260 −0.75
†
3967
500 −10.65 0 4000
1000 −42.60 0 4000
1500 −95.85 0 4000
2000 −175.40 0 4000
2500 −266.25 0 4000
*As calculated from Equation 6-29
†
From Figure 6-19
r
2
1
p(r, t) 4000
70.6 (300) (1.5) (1.25)
(60) (15)
E
i
948(.15)(1.5)(12 10
6
)r
2
(60) (t)
p(r, t) 4000 44.125 E
i
42.6(10
6
)
r
2
t
=+
×
−×
−
=+ −
−
Fundamentals of Reservoir Fluid Flow 379
Reservoir Eng Hndbk Ch 06a 2001-10-25 11:23 Page 379
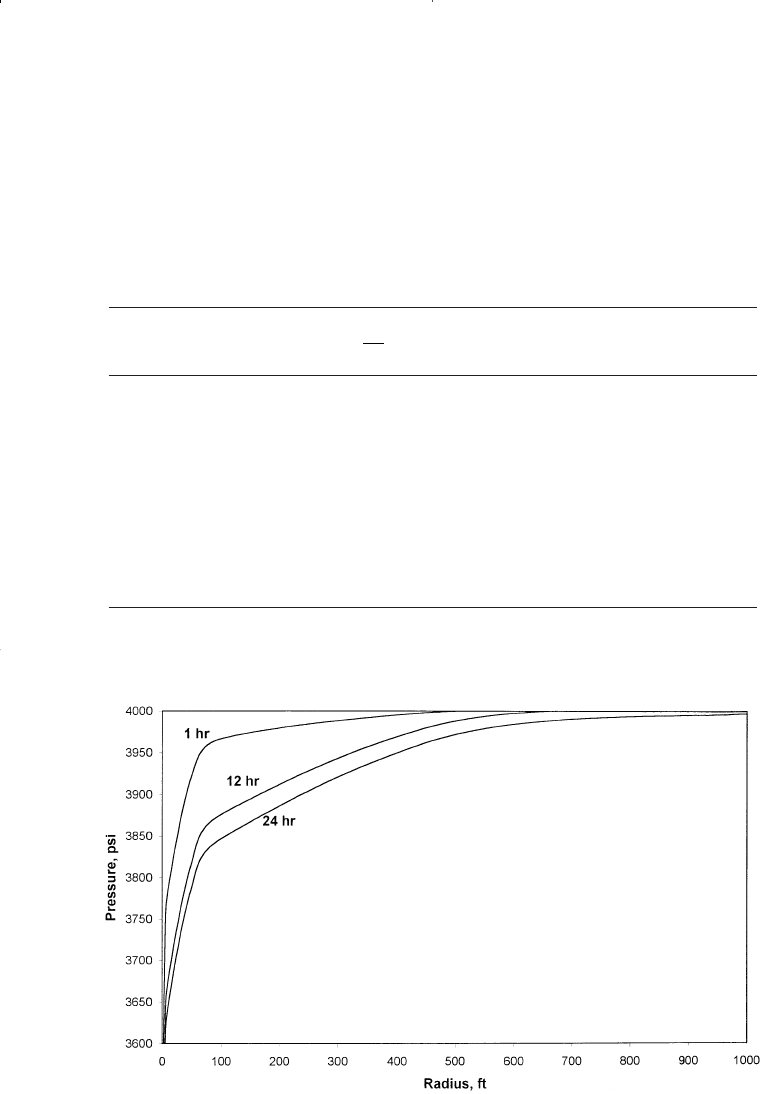
Step 3. Show results of the calculation graphically as illustrated in Fig-
ures 6-20 and 6-21.
Step 4. Repeat the calculation for t = 12 and 24 hrs.
Elapsed Time t = 12 hrs
r, ft x = 42.6(10
−6
)E
i
(−x) p(r,12) = 4000 + 44.125 E
i
(−x)
0.25 0.222 (10
−6
) −14.74* 3350
5 88.75 (10
−6
) −8.75* 3614
10 355.0 (10
−6
) −7.37* 3675
50 0.0089 −4.14* 3817
100 0.0355 −2.81
†
3876
500 0.888 −0.269 3988
1000 3.55 −0.0069 4000
1500 7.99 −3.77(10
−5
) 4000
2000 14.62 0 4000
2500 208.3 0 4000
*As calculated from Equation 6-29
†
From Figure 6-19
r
2
12
380 Reservoir Engineering Handbook
Figure 6-20. Pressure profiles as a function of time.
Reservoir Eng Hndbk Ch 06a 2001-10-25 11:23 Page 380
Elapsed Time t = 24 hrs
r, ft x = 42.6(10
−6
)E
i
(−x) p(r,24) = 4000 + 44.125 E
i
(−x)
0.25 −0.111 (10
−6
) −15.44* 3319
5 −44.38 (10
−6
) −9.45* 3583
10 −177.5 (10
−6
) −8.06* 3644
50 −0.0045 −4.83* 3787
100 −0.0178 −3.458
†
3847
500 −0.444 −0.640 3972
1000 −1.775 −0.067 3997
1500 −3.995 −0.0427 3998
2000 −7.310 8.24 (10
−6
) 4000
2500 −104.15 0 4000
*As calculated from Equation 6-29
†
From Figure 6-19
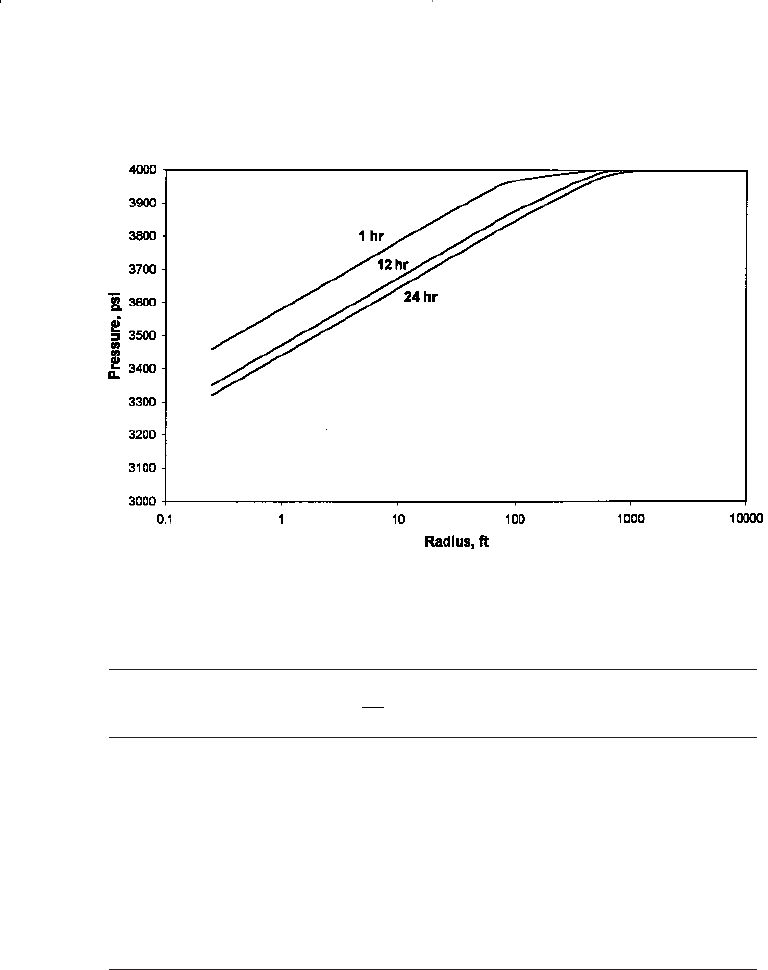
Step 5. Results of Step 4 are shown graphically in Figure 6-21.
The above example shows that most of the pressure loss occurs close
to the wellbore; accordingly, near-wellbore conditions will exert the
r
2
24
Fundamentals of Reservoir Fluid Flow 381
Figure 6-21. Pressure profiles as a function of time on a semi-log scale.
Reservoir Eng Hndbk Ch 06a 2001-10-25 11:23 Page 381
greatest influence on flow behavior. Figure 6-21 shows that the pressure
profile and the drainage radius are continuously changing with time.
When the parameter x in the E
i
-function is less than 0.01, the log
approximation as expressed by Equation 6-80 can be used in Equation
6-78 to give:
For most of the transient flow calculations, engineers are primarily
concerned with the behavior of the bottom-hole flowing pressure at the
wellbore, i.e., r = r
w
. Equation 6-82 can be applied at r = r
w
to yield:
where k = permeability, md
t = time, hr
c
t
= total compressibility, psi
−1
It should be noted that Equations 6-82 and 6-83 cannot be used until
the flow time t exceeds the limit imposed by the following constraint:
where t = time, hr
k = permeability, md
Example 6-11
Using the data in Example 6-10, estimate the bottom-hole flowing
pressure after 10 hours of production.
Solution
Step 1. Equation 6-83 can be used to calculate p
wf
only if the time
exceeds the time limit imposed by Equation 6-84, or:
t
cr
k
(6 - 84)
t
>×948 10
4
2
.
φµ
ο
pp
QB
kh
kt
fcr
wf i
ooo
otw
=−
−
162 6
323 6 83
2
.
log .
µ
µ
(- )
p(r, t) p
162.6 Q B
kh
log
kt
cr
3.23 (6 - 82)
i
ooo
ot
2
=− −
µ
φµ
382 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 06a 2001-10-25 11:23 Page 382

For all practical purposes, Equation 6-83 can be used anytime
during the transient flow period to estimate the bottom-hole
pressure.
Step 2. Since the specified time of 10 hr is greater than 0.000267 hrs, the
p
wf
can be estimated by applying Equation 6-83.
The second form of solution to the diffusivity equation is called the
dimensionless pressure drop and is discussed below.
The Dimensionless Pressure Drop (p
D
) Solution
Well test analysis often makes use of the concept of the dimensionless
variables in solving the unsteady-state flow equation. The importance of
dimensionless variables is that they simplify the diffusivity equation and
its solution by combining the reservoir parameters (such as permeability,
porosity, etc.) and thereby reduce the total number of unknowns.
To introduce the concept of the dimensionless pressure drop solution,
consider for example Darcy’s equation in a radial form as given previ-
ously by Equation 6-27.
Rearrange the above equation to give:
pp
QB
kh
r
r
ewf
ooo
e
w
−
=
µ
0 00708.
ln (6 - 85)
Q
o
= 0.00708
kh (p
e
− p
wf
)
µ
o
B
o
ln (r
e
/r
w
)
p
psi
wf
=−
×
×
−
=
−
4000
162 6 300 1 25 1 5
60 15
60 10
015 15 12 10 025
3 23 3358
62
.( )(. )(.)
()()
log
()()
(. )(.)( )(. )
.
thr=
×
=
=
−
94810
015 15 12 10 025
60
0 000267
0 153
4
62
.( )
(. )(.)( )(. )
.
. sec
Fundamentals of Reservoir Fluid Flow 383
Reservoir Eng Hndbk Ch 06a 2001-10-25 11:23 Page 383

It is obvious that the right hand side of the above equation has no units
(i.e., dimensionless) and, accordingly, the left-hand side must be dimen-
sionless. Since the left-hand side is dimensionless, and (p
e
− p
wf
) has the
units of psi, it follows that the term [Q
o
B
o
µ
o
/(0.00708kh)] has units of
pressure. In fact, any pressure difference divided by [Q
o
B
o
µ
o
/(0.00708kh)]
is a dimensionless pressure. Therefore, Equation 6-85 can be written in a
dimensionless form as:
p
D
= ln(r
eD
)
where
This concept can be extended to consider unsteady state equations
where the time is a variable. Defining:
In transient flow analysis, the dimensionless pressure p
D
is always a
function of dimensionless time that is defined by the following expression:
In transient flow analysis, the dimensionless pressure p
D
is always a
function of dimensionless time that is defined by the following expression:
The above expression is only one form of the dimensionless time.
Another definition in common usage is t
DA
, the dimensionless time based
on total drainage area.
t
kt
cr
D
tw
=
0 000264
2
.
φµ
(6 - 87)
p
pprt
QB
kh
D
i
ooo
=
−
(,)
.
µ
0 00708
(6 - 86)
r
r
r
eD
e
w
=
p
pp
QB
kh
D
ewf
ooo
=
−
µ
0 00708.
384 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 06a 2001-10-25 11:23 Page 384

where A = total drainage area =πr
e
2
r
e
= drainage radius, ft
r
w
= wellbore radius, ft
The dimensionless pressure p
D
also varies with location in the reser-
voir as represented by the dimensionless radial distances r
D
and r
eD
that
are defined by:
and
where p
D
= dimensionless pressure drop
r
eD
= dimensionless external radius
t
D
= dimensionless time
r
D
= dimensionless radius
t = time, hr
p(r,t) = pressure at radius r and time t
k = premeability, md
µ=viscosity, cp
The above dimensionless groups (i.e., p
D
, t
D
, and r
D
) can be introduced
into the diffusivity equation (Equation 6-76) to transform the equation
into the following dimensionless form:
Van Everdingen and Hurst (1949) proposed an analytical solution to
the above equation by assuming:
∂
∂
+
∂
∂
=
∂
∂
2
2
1
p
r
r
p
r
p
t
D
D
D
D
D
D
D
(6 - 90)
r
r
r
eD
e
w
= (6 - 89)
r
r
r
D
w
= (6 - 88)
t
kt
cA
t
r
A
DA
t
D
w
==
0 000264
2
.
φµ
(6 - 87a)
Fundamentals of Reservoir Fluid Flow 385
Reservoir Eng Hndbk Ch 06a 2001-10-25 11:23 Page 385

• Perfectly radial reservoir system
• The producing well is in the center and producing at a constant produc-
tion rate of Q
• Uniform pressure p
i
throughout the reservoir before production
• No flow across the external radius r
e
Van Everdingen and Hurst presented the solution to Equation 6-89 in a
form of infinite series of exponential terms and Bessel functions. The
authors evaluated this series for several values of r
eD
over a wide range
of values for t
D
. Chatas (1953) and Lee (1982) conveniently tabulated
these solutions for the following two cases:
• Infinite-acting reservoir
• Finite-radial reservoir
Infinite-Acting Reservoir
When a well is put on production at a constant flow rate after a shut-in
period, the pressure in the wellbore begins to drop and causes a pressure
disturbance to spread in the reservoir. The influence of the reservoir
boundaries or the shape of the drainage area does not affect the rate at
which the pressure disturbance spreads in the formation. That is why the
transient state flow is also called the infinite acting state. During the infi-
nite acting period, the declining rate of wellbore pressure and the manner
by which the pressure disturbance spreads through the reservoir are
determined by reservoir and fluid characteristics such as:
• Porosity, φ
• Permeability, k
• Total compressibility, c
t
• Viscosity, µ
For an infinite-acting reservoir, i.e., r
eD
=∞, the dimensionless pressure
drop function p
D
is strictly a function of the dimensionless time t
D
, or:
p
D
= f(t
D
)
Chatas and Lee tabulated the p
D
values for the infinite-acting reservoir
as shown in Table 6-2. The following mathematical expressions can be
used to approximate these tabulated values of p
D
:
386 Reservoir Engineering Handbook
Reservoir Eng Hndbk Ch 06a 2001-10-25 11:23 Page 386

Table 6-2
p
D
vs. t
D
—Infinite-Radial System, Constant-Rate at the Inner
Boundary (After Lee, J., Well Testing, SPE Textbook Series.)
(Permission to publish by the SPE, copyright SPE, 1982)
t
D
p
D
t
D
p
D
t
D
p
D
0 0 0.15 0.3750 60.0 2.4758
0.0005 0.0250 0.2 0.4241 70.0 2.5501
0.001 0.0352 0.3 0.5024 80.0 2.6147
0.002 0.0495 0.4 0.5645 90.0 2.6718
0.003 0.0603 0.5 0.6167 100.0 2.7233
0.004 0.0694 0.6 0.6622 150.0 2.9212
0.005 0.0774 0.7 0.7024 200.0 3.0636
0.006 0.0845 0.8 0.7387 250.0 3.1726
0.007 0.0911 0.9 0.7716 300.0 3.2630
0.008 0.0971 1.0 0.8019 350.0 3.3394
0.009 0.1028 1.2 0.8672 400.0 3.4057
0.01 0.1081 1.4 0.9160 450.0 3.4641
0.015 0.1312 2.0 1.0195 500.0 3.5164
0.02 0.1503 3.0 1.1665 550.0 3.5643
0.025 0.1669 4.0 1.2750 600.0 3.6076
0.03 0.1818 5.0 1.3625 650.0 3.6476
0.04 0.2077 6.0 1.4362 700.0 3.6842
0.05 0.2301 7.0 1.4997 750.0 3.7184
0.06 0.2500 8.0 1.5557 800.0 3.7505
0.07 0.2680 9.0 1.6057 850.0 3.7805
0.08 0.2845 10.0 1.6509 900.0 3.8088
0.09 0.2999 15.0 1.8294 950.0 3.8355
0.1 0.3144 20.0 1.9601 1,000.0 3.8584
30.0 2.1470
40.0 2.2824
50.0 2.3884
Notes: For t
D
< 0.01, p
D
≅ 2 Zt
D
/x.
For 100 < t
D
< 0.25 r
2
eD
, p
D
≅ 0.5 (ln t
D
+ 0.80907).
• For t
D
< 0.01:
• For t
D
> 100:
p
D
= 0.5[ln(t
D
) + 0.80907] (6 - 92)
p
t
D
D
= 2
π
(6 - 91)
Fundamentals of Reservoir Fluid Flow 387
Reservoir Eng Hndbk Ch 06a 2001-10-25 11:23 Page 387
