Tarek Ahmed. Reservoir engineering handbook

Подождите немного. Документ загружается.

The gas flow rate is usually measured at base (atmospheric) pressure p

and, therefore, the term Q

gsc

is introduced into Equation 4-41 to produce:

gsc

= q

where Q

gsc

= gas flow rate at standard conditions, cm

/sec

= base pressure (atmospheric pressure), atm

Substituting Darcy’s Law in the above expression gives

where k = absolute permeability, Darcys

= gas viscosity, cp

= base pressure, atm

= inlet (upstream) pressure, atm

= outlet (downstream) pressure, atm

L = length of the core, cm

A = cross-sectional area, cm

gsc

= gas flow rate at standard conditions, cm

/sec

The Klinkenberg Effect

Klinkenberg (1941) discovered that permeability measurements made

with air as the flowing fluid showed different results from permeability

measurements made with a liquid as the flowing fluid. The permeability

of a core sample measured by flowing air is always greater than the per-

meability obtained when a liquid is the flowing fluid. Klinkenberg postu-

lated, on the basis of his laboratory experiments, that liquids had a zero

velocity at the sand grain surface, while gases exhibited some finite

velocity at the sand grain surface. In other words, the gases exhibited

slippage at the sand grain surface. This slippage resulted in a higher flow

rate for the gas at a given pressure differential. Klinkenberg also found

that for a given porous medium as the mean pressure increased the calcu-

lated permeability decreased.

gsc

k A (

)

(4 - 42)

gsc

k A (

)

228 Reservoir Engineering Handbook

Reservoir Eng Hndbk Ch 04a 2001-10-24 09:37 Page 228

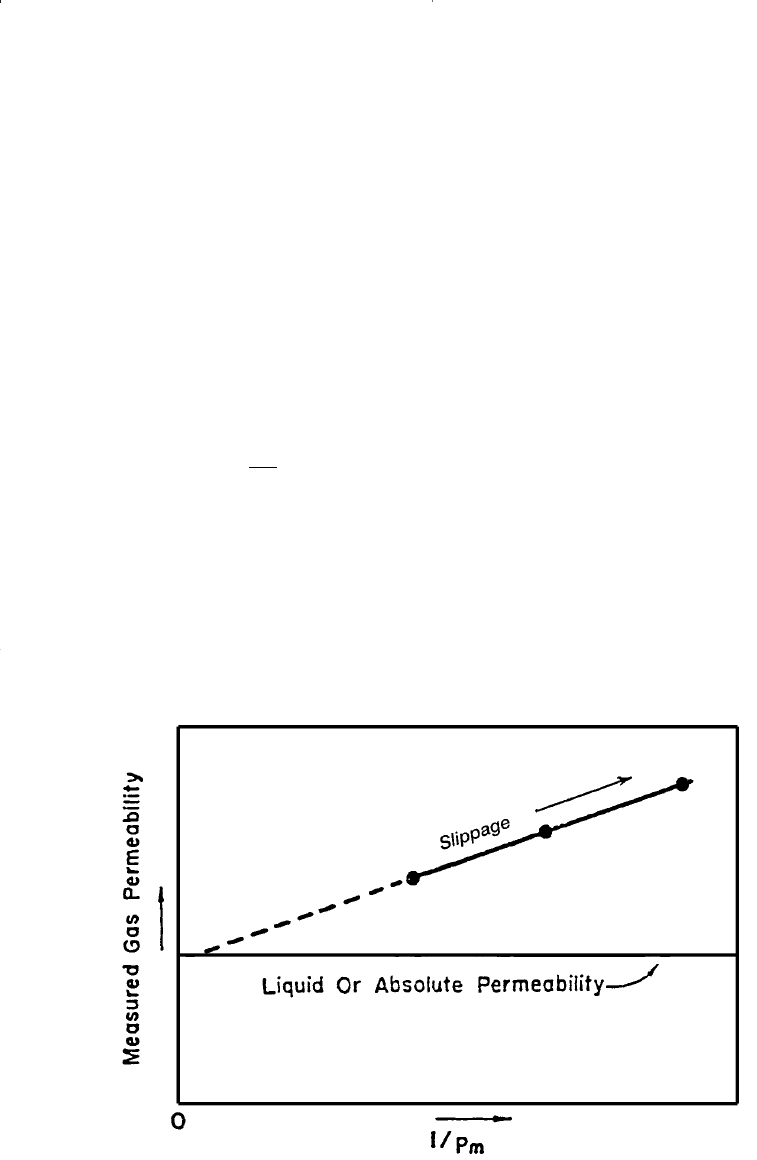
Fundamentals of Rock Properties 229

Mean pressure is defined as upstream flowing plus downstream flow-

ing pressure divided by two, [p

= (p

+ p

)/2]. If a plot of measured per-

meability versus 1/p

were extrapolated to the point where 1/p

= 0, in

other words, where p

= infinity, this permeability would be approxi-

mately equal to the liquid permeability. A graph of this nature is shown in

Figure 4-21. The absolute permeability is determined by extrapolation as

shown in Figure 4-21.

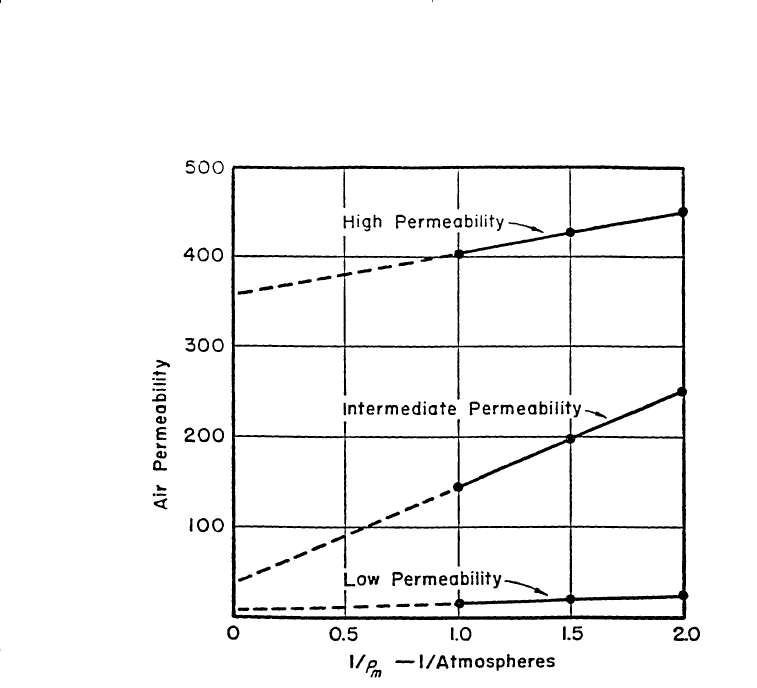
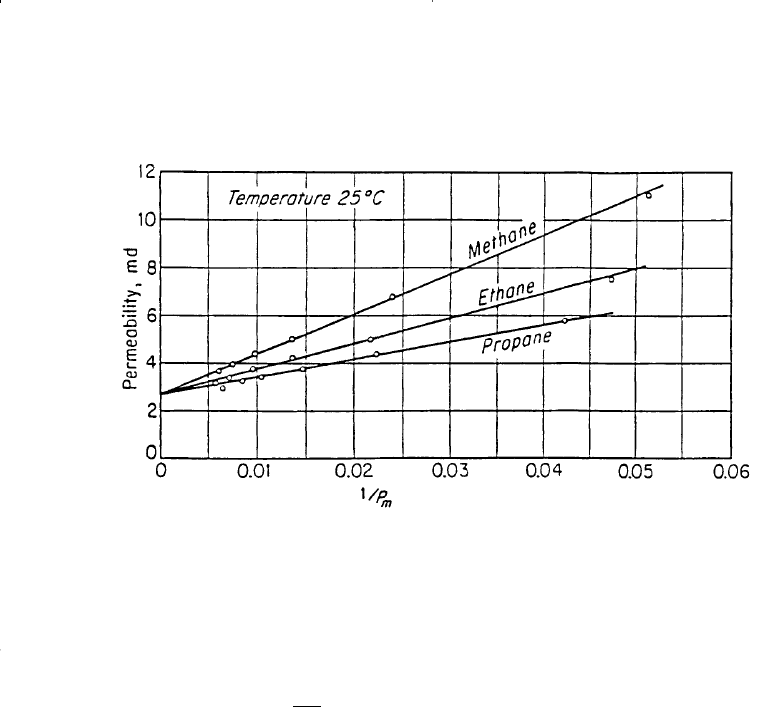
The magnitude of the Klinkenberg effect varies with the core perme-

ability and the type of the gas used in the experiment as shown in Figures

4-22 and 4-23. The resulting straight-line relationship can be expressed as

where k

= measured gas permeability

= mean pressure

= equivalent liquid permeability, i.e., absolute permeability, k

c = slope of the line

(4 - 43)

Figure 4-21. The Klinkenberg effect in gas permeability measurements.

Reservoir Eng Hndbk Ch 04b 2001-10-24 09:46 Page 229

Klinkenberg suggested that the slope Ac @ is a function of the follow-

ing factors:

• Absolute permeability k, i.e., permeability of medium to a single phase

completely filling the pores of the medium k

• Type of the gas used in measuring the permeability, e.g., air.

• Average radius of the rock capillaries.

Klinkenberg expressed the slope c by the following relationship:

c = bk

(4-44)

where k

= equivalent liquid permeability, i.e., absolute permeability, k

b = constant which depends on the size of the pore openings

and is inversely proportional to radius of capillaries.

230 Reservoir Engineering Handbook

Figure 4-22. Effect of permeability on the magnitude of the Klinkenberg effect.

(After Cole, F., 1969.)

Reservoir Eng Hndbk Ch 04b 2001-10-24 09:46 Page 230

Combining Equation 4-44 with 4-43 gives:

where k

is the gas permeability as measured at the average pressure p

Jones (1972) studied the gas slip phenomena for a group of cores for

which porosity, liquid permeability k

(absolute permeability), and air

permeability were determined. He correlated the parameter b with the

liquid permeability by the following expression:

b = 6.9 k

-0.36

(4-46)

The usual measurement of permeability is made with air at mean pres-

sure just above atmospheric pressure (1 atm). To evaluate the slip phe-

nomenon and the Klinkenberg effect, it is necessary to at least measure

the gas permeability at two mean-pressure levels. In the absence of such

data, Equations 4-45 and 4-46 can be combined and arranged to give:

6.9 k

0.64

+ p

- p

= 0 (4-47)

gL L

()

(4 - 45)

Fundamentals of Rock Properties 231

Figure 4-23. Effect of gas pressure on measured permeability for various gases.

(After Calhoun, J., 1976.)

Reservoir Eng Hndbk Ch 04b 2001-10-24 09:46 Page 231

where p

= mean pressure, psi

= air permeability at p

, psi

= absolute permeability (k), md

Equation 4-47 can be used to calculate the absolute permeability when

only one gas permeability measurement (k

) of a core sample is made at

. This nonlinear equation can be solved iteratively by using the New-

ton-Raphson iterative methods. The proposed solution method can be

conveniently written as

where k

= initial guess of the absolute permeability, md

i+1

= new permeability value to be used for the next iteration

i = iteration level

f(k

) = Equation 4-47 as evaluated by using the assumed value of k

f¢(k

) = first-derivative of Equation 4-47 as evaluated at k

The first derivative of Equation 4-47 with respect to k

is:

f¢ (k

) = 4.416 k

-0.36

+ p

(4-48)

The iterative procedure is repeated until convergence is achieved when

f(k

) approaches zero or when no changes in the calculated values of k

are observed.

Example 4-10

The permeability of a core plug is measured by air. Only one measure-

ment is made at a mean pressure of 2.152 psi. The air permeability is

46.6 md. Estimate the absolute permeability of the core sample. Compare

the result with the actual absolute permeability of 23.66 md.

Solution

Step 1. Substitute the given values of p

and k

into Equations 4-47 and

4-48, to give:

f (k

) = 6.9 k

0.64

+ 2.152 k

- (2.152) (46.6) f¢ (k

) = 4.416 k

-0.36

+ 2.152

i+1 i

f (

)

f (

)

232 Reservoir Engineering Handbook

Reservoir Eng Hndbk Ch 04b 2001-10-24 09:46 Page 232

Step 2. Assume k

= 30 and apply the Newton-Raphson method to find

the required solution as shown below.

f(k

)f¢(k

i + 1

1 30.000 25.12 3.45 22.719

2 22.719 -0.466 3.29 22.861

3 22.861 0.414 3.29 22.848

After three iterations, the Newton-Raphson method converges to an

absolute value for the permeability of 22.848 md.

Equation 4-39 can be expanded to describe flow in any porous medi-

um where the geometry of the system is not too complex to integrate. For

example, the flow into a well bore is not linear, but is more often radial.

Figure 4-24 illustrates the type of flow that is typical of that occurring in

the vicinity of a producing well. For a radial flow, Darcy’s equation in a

differential form can be written as:

Fundamentals of Rock Properties 233

Figure 4-24. Radial flow model.

Reservoir Eng Hndbk Ch 04b 2001-10-24 09:46 Page 233

Integrating Darcy’s equation gives:

The term dL has been replaced by dr as the length term has now

become a radius term. The minus sign is no longer required for the radial

system shown in Figure 4-24 as the radius increases in the same direction

as the pressure. In other words, as the radius increases going away from

the well bore, the pressure also increases. At any point in the reservoir,

the cross-sectional area across which flow occurs will be the surface area

of a cylinder, which is 2prh. Since the cross-sectional area is related to r,

then A must be included within the integral sign as follows:

dr =

kA dp

234 Reservoir Engineering Handbook

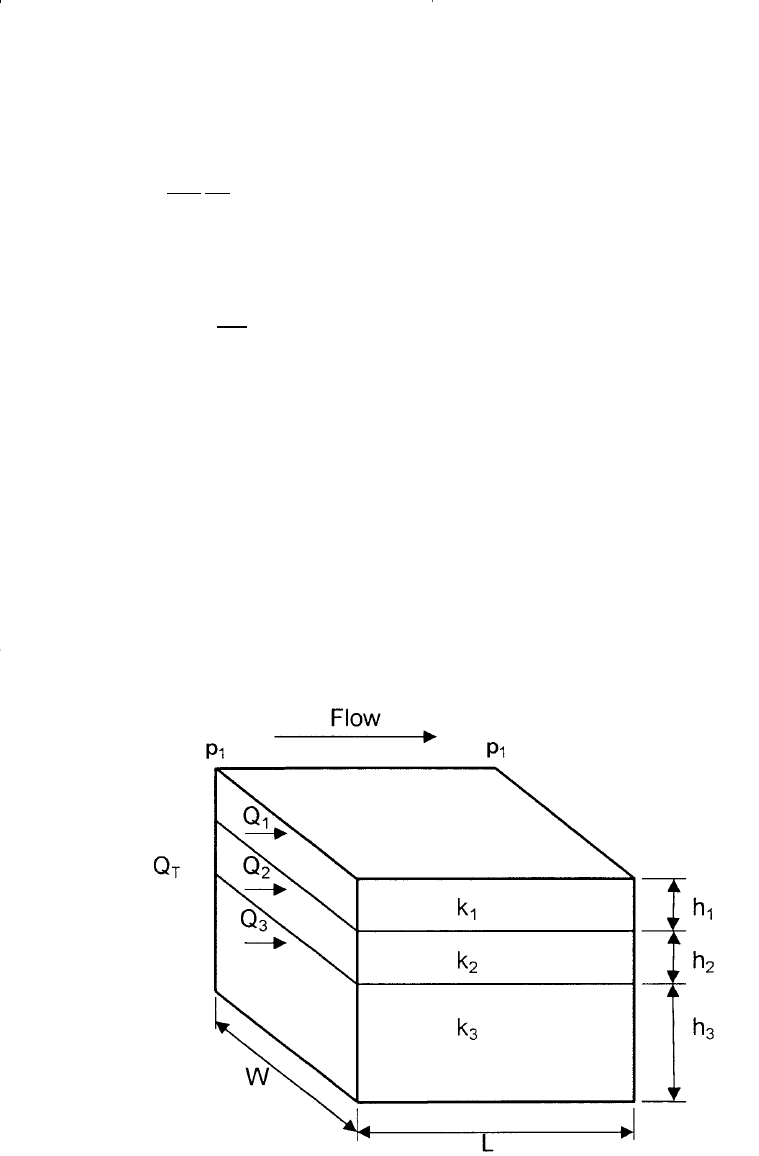
Figure 4-25. Linear flow through layered beds.

Reservoir Eng Hndbk Ch 04b 2001-10-24 09:46 Page 234

rearranging

and integrating

Solving for the flow rate, q, results in:

The above equation assumes that the reservoir is homogeneous and is

completely saturated with a single liquid phase (appropriate modifica-

tions will be discussed in later sections to account for the presence of

other fluids), where:

q = flow rate, reservoir cm

/sec

k = absolute permeability, Darcy

h = thickness, cm

= drainage radius, cm

= well bore radius, cm

= pressure at drainage radius, atm

= bottom-hole flowing pressure

m=viscosity, cp

Averaging Absolute Permeabilities

The most difficult reservoir properties to determine usually are the

level and distribution of the absolute permeability throughout the reser-

voir. They are more variable than porosity and more difficult to measure.

Yet an adequate knowledge of permeability distribution is critical to the

2 kh (

)

ewf

ln ( )

(4 - 49)

2 h

(

)

ewf

ln ln--

2 h

ÚÚ

2 rh

ÚÚ

Fundamentals of Rock Properties 235

Reservoir Eng Hndbk Ch 04b 2001-10-24 09:46 Page 235

prediction of reservoir depletion by any recovery process. It is rare to

encounter a homogeneous reservoir in actual practice. In many cases, the

reservoir contains distinct layers, blocks, or concentric rings of varying

permeabilities. Also, because smaller-scale heterogeneities always exist,

core permeabilities must be averaged to represent the flow characteristics

of the entire reservoir or individual reservoir layers (units). The proper

way of averaging the permeability data depends on how permeabilities

were distributed as the rock was deposited.

There are three simple permeability-averaging techniques that are

commonly used to determine an appropriate average permeability to rep-

resent an equivalent homogeneous system. These are:

• Weighted-average permeability

• Harmonic-average permeability

• Geometric-average permeability

Weighted-Average Permeability

This averaging method is used to determine the average permeability

of layered-parallel beds with different permeabilities. Consider the case

where the flow system is comprised of three parallel layers that are sepa-

rated from one another by thin impermeable barriers, i.e., no cross flow,

as shown in Figure 4-25. All the layers have the same width w with a

cross-sectional area of A.

The flow from each layer can be calculated by applying Darcy’s equa-

tion in a linear form as expressed by Equation 4-40, to give:

Layer 1

Layer 2

Layer 3

kwh p

236 Reservoir Engineering Handbook

Reservoir Eng Hndbk Ch 04b 2001-10-24 09:46 Page 236

The total flow rate from the entire system is expressed as

where q

= total flow rate

avg

= average permeability for the entire model

w = width of the formation

Dp = p

B p

= total thickness

The total flow rate q

is equal to the sum of the flow rates through each

layer or:

= q

+ q

Combining the above expressions gives:

The average absolute permeability for a parallel-layered system can be

expressed in the following form:

Equation 4-50 is commonly used to determine the average permeabili-

ty of a reservoir from core analysis data.

avg

(4 - 50)

avg t 2 2

avg

11 22 33

11 33

avg t

11 2 2 3 3

DDD

mmmm

kwhp

avg t

Fundamentals of Rock Properties 237

Reservoir Eng Hndbk Ch 04b 2001-10-24 09:46 Page 237