Tabak J. Mathematics and the Laws of Nature: Developing the Language of Science
Подождите немного. Документ загружается.


110 MATHEMATICS AND THE LAWS OF NATURE
to flow, that motion is transmitted to other parts of the fluid, and
soon the entire mass begins to swirl around. This coupling of the
motion in one part of a fluid with motions in other parts causes
complex, beautiful, and often surprising patterns of flow.
The development of computers has been a great help in under-
standing some of the properties of the solutions of equations of
fluid dynamics, but computational solutions leave many problems
unresolved as well. For example, the fact that the computer can
find a solution is no guarantee that another solution does not exist
for the same situation. It may be that one set of equations has mul-
tiple solutions for the same “input” or set of initial conditions. The
existence of multiple solutions is critical, because if other, different
solutions exist for the same set of conditions, then predicting the
behavior of the fluid becomes much more difficult. This is one
reason that there are still many mathematicians who devote their
time to studying very basic, noncomputational questions about
the nature of the equations that arise in the study of fluids. Euler
founded the science of mathematical fluid dynamics, but his main
contribution lies in the statement of the problem rather than in
any solutions that he obtained.
Limits on the Applicability of Conservation of Mass
In order to better appreciate the way that the law of conserva-
tion of mass is used in science today, consider the results of early
experiments on atomic nuclei and the protons and neutrons of
which they are composed. (Atomic nuclei contain two types of
particles, protons, each of which has a positive electrical charge,
and neutrons, which have no electrical charge.) As the 20th cen-
tury progressed, physicists became increasingly adept at measur-
ing the mass of atomic nuclei as well as single protons and single
neutrons. A reasonably accurate modern value for the mass of
a proton, for example, is 1.6726231×10
–27
kg. (Without scien-
tific notation this number would begin with a decimal point; the
decimal point would be followed by 26 zeros and then the digits
16726231.) Neutrons are just slightly more massive than protons.
In order to avoid long strings of not-very-meaningful digits, let m
p

Mathematics and the Law of Conservation of Mass 111
represent the mass of a proton and let m
n
represent the mass of a
neutron. If the law of conservation of mass were valid in nuclear
physics, which is the branch of science concerned with studying
the properties of protons and neutrons, then a nucleus that con-
sisted of j protons and k neutrons would have a mass of j×m
p
+ k×m
n
kg. (This expression is just the mass of j protons added to the mass
of k neutrons.) This is, after all, exactly the procedure that we use
to add masses in all our day-to-day situations. If, for example, we
had j identical cups, each of which had a mass of m
c
kilograms and
k saucers, each of which had a mass of m
s
kilograms, then the mass
of the set of j cups and k saucers would be j×m
c
+ k×m
s
kilograms.
In the world as most of us know it, the mass of a set of individual
items is the sum of the individual masses in the set. This is a con-
sequence of the statement that mass is conserved.
But nuclear physicists demonstrated that the mass of a nucleus
of an atom consisting of j protons and k neutrons was somewhat
smaller than j×m
p
+ k×m
n
kg. Mass was missing from the nucleus
in the sense that the mass of the sum was smaller than the sum of
the individual masses. What had happened to the missing mass?
The answer is that mass and energy can be converted one into
the other according to the following rule, which was first proposed
by the German-American physicist Albert Einstein (1879–1955):
E = mc
2
where the letter E represents energy; the letter m represents mass,
and the letter c represents the speed of light. (The superscript 2,
which, when attached to the c, is read “c-squared” is shorthand
for c×c.) Einstein’s famous equation contradicts the law of con-
servation of mass. According to the formula, mass need not be
conserved because it can be converted into energy. The equation
states that in an isolated system, when m units of mass “go miss-
ing,” the energy of the system should increase by mc
2
.
To return to the problem of the nucleus and the missing mass,
the forces that bind protons and neutrons within the nucleus
are very strong. When a nucleus is formed, some of the mass of
its constituent protons and neutrons is converted into binding

112 MATHEMATICS AND THE LAWS OF NATURE
energy. This explains why the mass of the nucleus is less than the
sum of the masses of the individual protons and neutrons of which
it is comprised. But this contradicts the statement that mass is
conserved. How, then, can engineers and scientists continue to use
the principle of conservation of mass in their models?
The conversion of mass into energy is, in a sense, a common
reaction. It occurs throughout the universe. Mass-energy conver-
sion is, for example, what makes stars shine. But for most “ordi-
nary” phenomena such as the weather, combustion, manufacturing
processes, photosynthesis, digestion, . . . almost everything that we
encounter in our day-to-day lives, the conversion of mass into
energy (and energy into mass) does not play an important role.
How is the word important defined in this context? An effect is
not important if it is too small to measure. To see how this idea
applies in practice consider chemical rather than nuclear reactions.
Chemical reactions involve molecules, and molecules are com-
posed of multiple atoms bound together by forces that are much
weaker than the forces that bind protons and neutrons together
in a nucleus. But Einstein’s equation still applies. It applies every-
where—to chemical as well as nuclear reactions. There is, there-
fore, a similar “missing mass” type of phenomenon for molecules,
but the effect is very small—so small that even very sensitive
instruments cannot detect it. A chemical engineer who wants to
use a mathematical model to describe a manufacturing process—
and the process might involve producing anything from a breakfast
cereal to a medicine—could include terms in the model to account
for energy-mass conversion, but no engineer would include such
terms because they complicate the model without improving its
accuracy. The value of a mathematical model is not determined by
whether it incorporates every term that could be included; a good
mathematical model incorporates only those terms that should be
included, and there is a big difference between could and should.
Today, most scientists and engineers continue to develop math-
ematical models of physical systems using laws of nature that state
that mass and energy are completely separate characteristics of
the systems. Mass is conserved; energy is conserved; and they are
conserved separately. These models do not, therefore, take into

Mathematics and the Law of Conservation of Mass 113
account the possibility that mass can be converted into energy and
energy into mass. This is not a weakness but a strength of these
models. The assumption of separate conservation laws for mass
and energy make the resulting equations easier to solve with no
appreciable loss of accuracy. Of course, scientists and engineers
involved in nuclear physics cannot treat matter and energy as
entirely separate quantities. If they incorporate the statement that
mass is conserved into their models of nuclear phenomena they
can expect “wrong” results in the sense that their predictions will
be at variance with their subsequent measurements. The decision
to incorporate the law of conservation of mass into a mathemati-
cal model is not based on whether the law is true or false, right or
wrong, but whether the resulting model is useful. A useful model
is one that enables the engineer or scientist to better understand
the phenomenon of interest. A good model facilitates progress.
This is a modern view. For many years after Lavoisier, research-
ers believed that the law of conservation of mass stated an exact
truth about nature. They had created a model of nature, but
they mistook their model for reality. Contemporary researchers
are generally much more careful about distinguishing between a
natural phenomenon and a model of that same phenomenon, and
the law of conservation of mass is a nice illustration of why that
distinction has become so important to keep in mind.

114
7
mathematics and
the laws of
thermodynamics
Thermodynamics is that branch of science that deals with the
relationships that exist between heat and work. In a practical sense
thermodynamics is concerned with our ability to turn heat energy
into electrical energy, as is done at oil, coal, gas, and nuclear power
plants. It is also concerned with the problem of turning heat
energy into the energy of motion, as in cars, ships, and planes.
But thermodynamics also has a theoretical side. Theoretically
thermodynamics is concerned with energy, work, and the concept
of irreversibility. (A process is irreversible if it cannot be undone;
combustion, for example, is an irreversible process.) More than
most branches of science thermodynamics is also a subject that
has inspired a great deal of philosophical speculation. It touches
on important questions about why physical systems evolve in some
ways but not others. It is one of the conceptually richest areas of
classical physics.
A Failed Conservation Law
The history of thermodynamics traces its roots to experiments
performed by the Italian physicist and mathematician Galileo
Galilei. Galileo is often given credit for being the first to devise
a thermometer. In the study of heat a thermometer is a valuable
tool. It enables the user to measure changes in temperature and
to compare the temperature of various objects and materials by

Mathematics and the Laws of Thermodynamics 115
“taking” their temperatures. Galileo’s invention was an important
innovation because two objects at the same temperature often feel
as if they are at different temperatures. For example, if we touch
a slab of wood and a slab of iron, both of which are at room tem-
perature, the iron feels cooler. Thermometers provide an objec-
tive way of comparing temperatures, but they do not offer much
insight into what temperature is.
The study of thermodynamics began in earnest with the work of
the French-born British inventor and scientist Denis Papin (1647–
1712). Papin was well connected; he had already worked with the
Dutch physicist, mathematician, and inventor Christiaan Huygens
and the British physicist Robert Boyle before he began to think
about steam. Papin invented what he called a “digester,” which
is what we would call a pressure cooker. The goal was to turn
water to steam in a sealed container. The result is that pressure in
the container quickly increases. The boiling temperature of the
water also rapidly increases. Pressure cookers are useful devices
for cooking food provided the containers do not explode. Papin’s
solution to the problem of exploding containers was to design a
safety valve. When the pressure increased enough, it raised the
valve and released some of the pressure. It was Papin’s insight that
the pressure that the
steam exerted on the
safety valve might also
drive a piston. As the
piston rose it could be
made to raise a weight
or do other useful work.
Papin’s idea of driving
a piston with steam was
soon incorporated into
a practical steam-driv-
en pump by the British
inventor Thomas Savery
(ca. 1650–1715). Savery
received the first pat-
ent for a steam-driven
The first steam engine designed and built in
the United States, 1801. Inventors and engi-
neers successfully constructed steam engines
before the principles on which they operated
were completely understood.
(Library of
Congress, Prints & Photographs Division)

116 MATHEMATICS AND THE LAWS OF NATURE
pump, which was used to remove water from mines. Savery’s design
was crude but it was soon improved. Savery formed a partnership
with another British inventor, Thomas Newcomen (1663–1729).
The new engine that resulted from the partnership, designed by
Newcomen, was a substantial improvement, but it was still very
wasteful of energy.
Fortunately one of Newcomen’s engines broke and was taken to
a little-known repairman named James Watt (1736–1819). While
repairing the Newcomen engine, Watt saw a way that the efficien-
cy of the engine could be substantially improved. In 1769 James
Watt applied for his first steam engine patent. It was the first of
many patents that Watt received for improving the steam engine.
By the time he had finished his work on the steam engine, Watt’s
engines were installed in mines and factories throughout Britain,
and Watt had become a wealthy and celebrated man. The British
Industrial Revolution was now in full swing, and it was powered
by the Watt steam engine. The race to understand the relationship
between heat and work had begun.
Steam engines are heat engines. Anyone wishing to understand
the physical principles on which a steam engine is based must
also understand heat. James Watt’s friend and financial backer the
British chemist, physician, and physicist Joseph Black (1728–99)
was one of the first to make a serious attempt to understand the
nature of heat.
Black had received a very broad education at Glasgow University,
where he studied medicine and science, and at the University of
Edinburgh, where he studied medicine. Black later taught chem-
istry, anatomy, and medicine at the University of Glasgow. He was
also a practicing physician, but today he is remembered for his work
in chemistry and physics. In chemistry he showed that the color-
less, odorless gas carbon dioxide is a gas different from ordinary
air; these experiments preceded those of Lavoisier. In physics Black
undertook one of the first serious studies of the nature of heat. His
experiments with heat and his theory of heat are his most important
contributions to the history of the science of thermodynamics.
Black noticed several important properties of heat. He noticed
that the addition of heat to a body sometimes raises the tem-
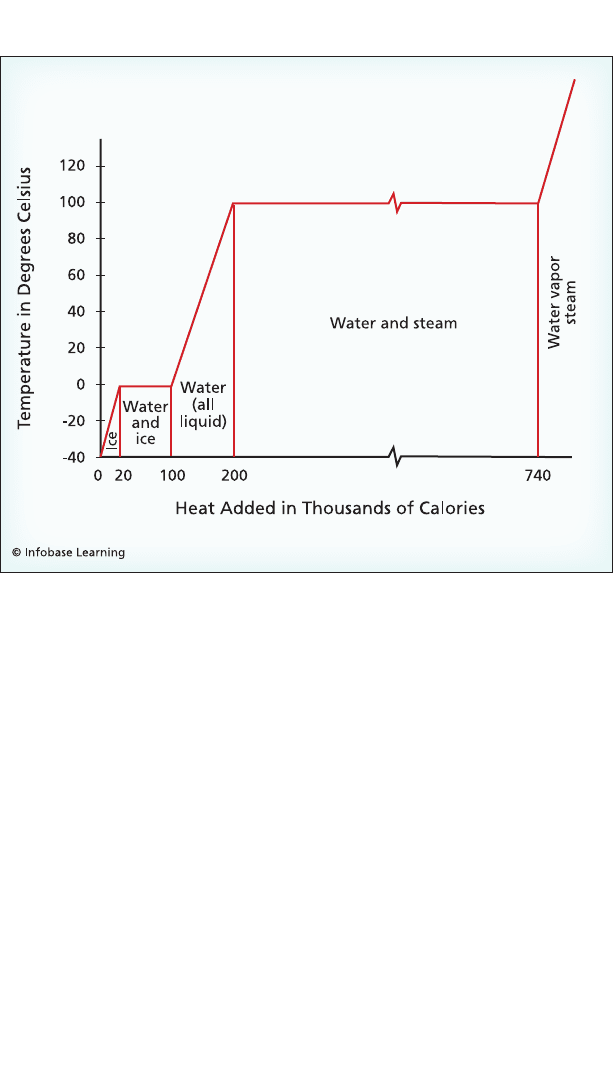
Mathematics and the Laws of Thermodynamics 117
perature of the body, but sometimes heat can be added to a body
without raising its temperature. For example, if heat is added to
a container of cool water, the water responds with an increase in
temperature. If, however, the water is already boiling, increasing
the rate at which heat is added simply causes the water to boil
faster; the temperature of the water does not change. Similarly
adding heat to a block of ice causes the temperature of the ice to
increase until it is at the temperature at which ice melts (32°F or
0°C). If additional heat is transferred while the ice is at the melting
Heat is steadily added to a block of ice initially at –40°C. As heat is
added: A) The ice warms until it reaches the melting point (sensible heat);
B) Additional heat causes the ice to melt but does not cause a change in
temperature (latent heat); C) Once the ice has melted, the temperature
increases steadily until the boiling point is reached (sensible heat); D) As
more heat is added the water boils with no change in temperature (latent
heat); E) When the water has turned to vapor, the temperature again
begins to increase (sensible heat).

118 MATHEMATICS AND THE LAWS OF NATURE
point, the ice melts, but its temperature does not increase until all
the ice has turned to water.
The change of any substance from vapor to liquid, or liquid
to vapor, or the change of any substance from liquid to solid, or
solid to liquid, is a phase change. (Matter generally exists in one of
three phases: vapor, liquid, or solid.) Black’s experiments showed
that when a material undergoes a phase change, the tempera-
ture remains constant until the phase change is complete. Black
responded to these observations by defining heat in terms of what
it does rather than what it is. He called heat that causes a change
in temperature sensible heat. He called heat that causes a change of
phase latent heat.
Black also noticed variations in what we now call the specific
heat of bodies. To understand the idea, imagine that we transfer
the same amount of heat to two liquids of identical mass. We may,
for example, use water and ethyl alcohol. Though the amount of
heat transferred to each body is the same, the resulting change in
temperature is different: The temperature of the alcohol increases
more than the temperature of the water. Furthermore not only
does the change in temperature vary with the material; so does the
amount of expansion or contraction as heat moves into or out of
the material. For Black and his contemporaries the complex inter-
actions that they observed between heat and matter were a barrier
to understanding the nature of heat.
After he had developed a significant body of experimental
results, Black created what he called the caloric theory to explain
what he had observed. Caloric, he hypothesized, is a fluid that
can flow from one body to another. When a warm body is placed
in contact with a cool body, caloric flows out of the warm body
into the cool one. The temperature of the warm body diminishes
as the temperature of the cool body increases. Furthermore as
caloric flows from one body to the other, the volume of the warm
body diminishes and the volume of the cool body increases.
Having hypothesized the existence of caloric, he was able to
deduce various properties that it must have in order to make his
theory consistent. The most important of these properties was
that caloric is conserved; that is, Black’s idea was that caloric, as

Mathematics and the Laws of Thermodynamics 119
well as momentum and mass, cannot be created or destroyed.
Black had proposed a new conservation law.
In retrospect seeing why Black believed caloric was conserved
is easy: Experiments had enabled him to determine how much
of an increase in caloric (heat) is needed to raise the tempera-
ture of a particular body a given number of degrees. He was
also able to measure how much of a decrease in caloric is neces-
sary to lower the temperature of that same body a given number
of degrees. When he placed two bodies in contact with each
other, he could compute the amount of caloric that flowed out
of one body into the other by taking the temperature of only
one of the bodies. This enabled him to compute the tempera-
ture change in the second body: A decrease in caloric in the first
body is reflected in an increase in caloric in the second body.
These findings are what led Black to conclude that caloric is
neither created nor destroyed; it is simply transferred from one
body to another.
Black’s conservation of caloric law was very influential. Many
of the best scientists of the day accepted it, but from the start
there were some dissenters as well. An early voice of dissent was
that of the American-born physicist, inventor, and administra-
tor Benjamin Thompson (1753–1814), also known as Count
Rumford. Thompson was a British loyalist during the American
Revolutionary War. He served as a British spy for part of the war
and later served as a British officer in New York. At the conclusion
of the war he wisely moved to Britain.
Thompson had a highly inventive mind. He lived for a time
in England and later moved to Bavaria. While there he invented
the drip coffeepot and a type of kitchen range. He improved the
design of fireplaces and chimneys. As an administrator in Bavaria
he introduced a number of social reforms and encouraged the
adoption of Watt’s steam engine technology. Most important
for the history of science, as director of the Bavarian arsenal
Thompson supervised the boring of cannons. The boring of can-
nons is slow, hot work. As the drill cuts into the metal, it produces
many small metal chips. The temperatures of the drill bit and the
cannon soar. Water is poured onto the bit to prevent both the bit
