СЗТУ Высшая математика
Подождите немного. Документ загружается.


( 1,2,..., ; 1,2,..., ).
ik ik
bai mk n=λ = =
Для произведения матрицы
A
на число
λ
используются обозначения
.BA
=
λ
Таким образом, если
A
=
11 12 1
21 22 2
12
...
...
... ... ... ...
...
n
n
mm mm
aa a
aa a
aa a
,
то
BA==
λ
11 12 1
21 22 2
12
...
...
... ... ... ...
...
n
n
mm mm
aa a
aa a
aa a
λλ λ
λλ λ
λλ λ
. (1.47)
Пример. Найти произведение матрицы
24
31
10
A
−
=
−
на число
3.λ=−
Решение. В соответствии с определением, имеем
24 612
333193
10 30
BA
−−
=− =− = − −
−
.
Свойства операции умножения матрицы на число
1. Распределительное свойство относительно числового и матричного множите-
лей:
(
)
,
A
AAλ+μ ⋅ =λ +μ
(1.48)
(
)
,
A
BABλ+=λ+λ
(1.49)
где - любые числа.
,λμ
2. Сочетательное свойство относительно числового множителя:
(
)
(
)
A
A
λμ
=λ
μ
. (1.50)
3.
1.
A
A
⋅
=
(1.51)
4.
,
mn mn
OO
λ
⋅=
(1.52)
50
где нулевая матрица любого размера.
mn
O −
5.
,
mn mn
OO
λ
⋅=
(1.53)
Для матриц одинакового размера можно определить разность
A
B
−
с по-
мощью равенства
(1).
A
BA B
−
=+−
(1.54)
Умножение матриц
Операция умножения двух матриц определена только для тех случаев, ко-
гда число столбцов первого сомножителя равно числу строк у второго.
Определение. Произведением матрицы
A
размера на матрицу
mn×
B
размера называется матрица размера
np×
C
mp
×
, каждый элемент которой
ik
c
равен сумме произведений элементов -й строки матрицы
i
A
на соответст-
вующие элементы -го столбца матрицы , то есть
k
B
(
)
11 2 2
1, 2,..., ; 1,2,...,
ik i k i k im mk
cabab ab i mk p= + +⋅⋅⋅+ = =
. (1.55)
Для произведения матриц
A
и используется обозначение
B
CAB=⋅
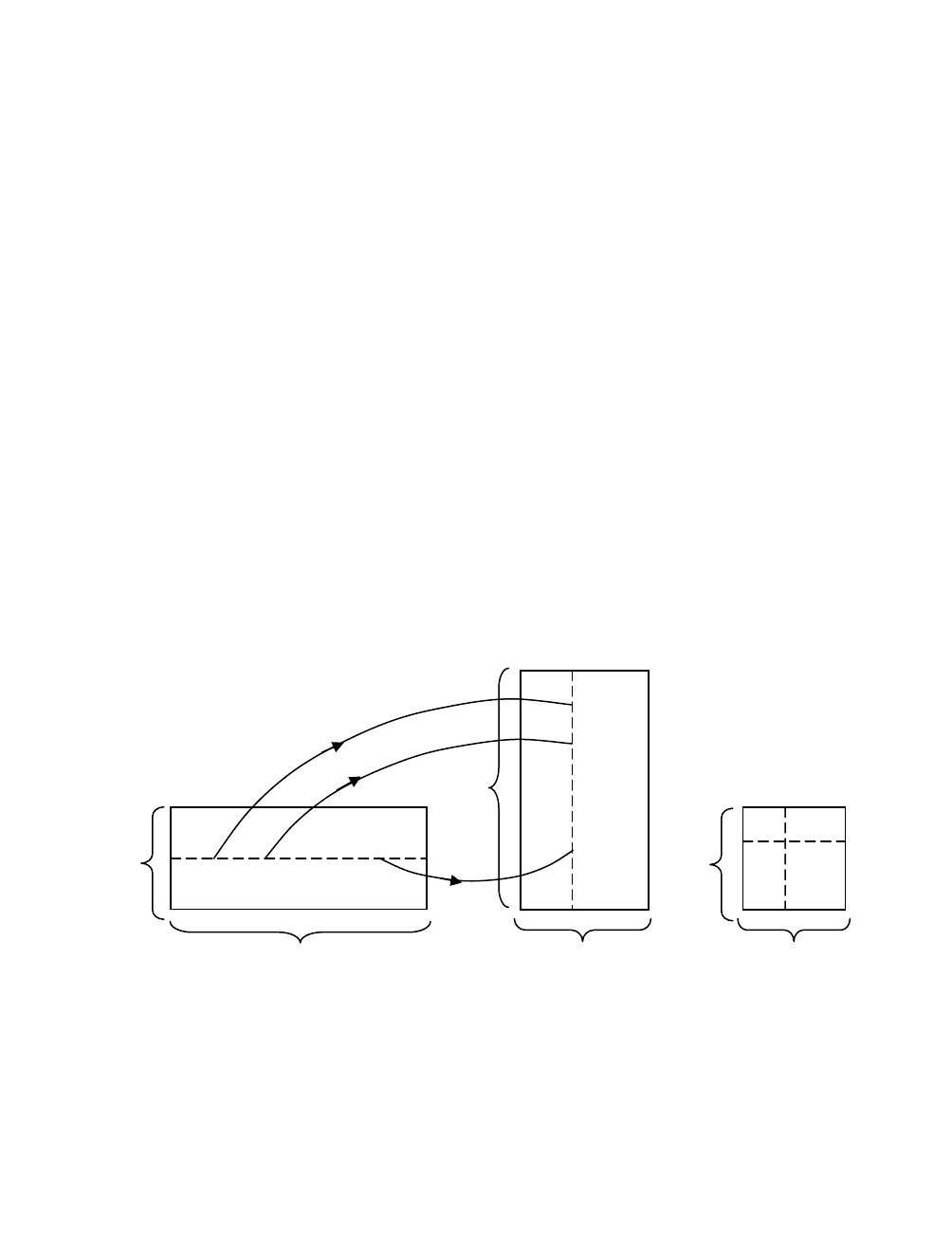
Это правило условно отражено на схеме.
Умножение матриц не обладает переместительным свойством, т.е. неком-
мутативно.
()
B
np
×
k
В связи с этим принято говорить об умножении данной матрицы
A
на мат-
рицу слева или справа. Произведение
B
A
B
называется произведением матрицы
A
на матрицу справа, а произведение - произведением матрицы
B BA
A
на мат-
рицу слева.
B
Исключение составляют так называемые перестановочные матрицы, для
которых
A
BBA=
. Например, матрицы
=
.
()cm p×
i
()Am n×
k
p
p
n
m
n
i
1i
a
2i
a
in
a
ik
c
1k
b
2k
b
nk
b
51

35
12
A =
и
15
.
12
B
−
=
−
перестановочны, так как
25
11
AB BA
−
−
==
−
−
.
Основные свойства операции умножения матриц
1. Сочетательное свойство относительно числового и матричного множи-
телей:
()() (),
A
BABABλ=λ=λ
(1.56)
(AB)C=A(BC). (1.57)
2. Распределительное свойство относительно сложения:
() .
A
B C AC BC
+
=+
(1.58)
3. Транспонирование произведения двух матриц равносильно произведе-
нию транспонированных матриц, взятых в обратном порядке, то есть
()
Т TT
.
A
BBA=
(1.59)
4. Определитель произведения квадратных матриц
A
и
B
равен произведе-
нию определителей этих матриц:
() ()().
D
AB D A D B
=
⋅
(1.60)
5 .Произведение произвольной матрицы
A
размера
mn
×
на единичную
матрицу
n
E
справа и на единичную матрицу
m
E
слева равно матрице
A
, то есть
;.
nm
A
EAEAA
=
=
(1.61)
В частности, для любой квадратной матрицы
A
n
-го порядка
.
nn
A
EEAA
=
=
(1.62)
Обратная матрица
Как известно, для каждого числа
0a
≠
существует такое число , что
b
1.ab⋅=
Число называется обратным для числа . Распространяя эту идею на
b
a
квадратные матрицы, поставим вопрос о существовании обратной матрицы, то
есть такой матрицы, которая в произведении с данной матрицей дает единичную
матрицу
E
.
Определение. Квадратная матрица
A
называется обратимой, если суще-
ствует квадратная матрица
X
, удовлетворяющая соотношениям
.
A
XXAE
=
=
(1.63)
Всякая матрица
X
, удовлетворяющая равенствам (1.63), называется об-
ратной по отношению к матрице
A
и обозначается
1
A
−
.
Можно доказать, что у каждой обратимой матрицы
A
существует лишь
единственная обратная матрица.
52
В условия (1.63) матрицы
A
и
X
входят симметрично. Следовательно, ес-
ли матрица
A
- обратная для
X
, то матрица
X
- обратная для
A
, то есть
11
()
A
A
−−
=
. (1.64)
Выясним, при каких условиях квадратная матрица обратима.
Теорема 1.3. Для того, чтобы матрица
A
имела обратную матрицу, необ-
ходимо и достаточно, чтобы ее определитель не равнялся нулю.
Квадратную матрицу
A
, определитель которой
()
D
A
отличен от нуля, на-
зывают невырожденной или неособенной. Если
() 0DA
=
, то матрица называет-
ся вырожденной или особенной.
У всякой неособенной матрицы
A
порядка существует одна и только
n
одна обратная матрица, которая может быть найдена по формуле
1
11 21
11 21 1
2
12 22
12 22 2
1
12
12
() () ()
1
() () ()
()
() () ()
n
n
n
n
nn nn
nn nn
A
AA
D
ADA DA
AA A
A
AA
AA A
D
ADA DA
A
DA
AA A
AA A
D
ADA DA
−
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
==
⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅
⋅
⋅⋅ ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
. (1.65).
Решение системы линейных уравнений при помощи матриц
Пусть дана система линейных уравнений с неизвестными
n n
12
, ,..., :
n
x
xx
11 1 12 2 1 1
21 1 22 2 2 2
11 2 2
,
,
........................
.
nn
nn
nn nnn
ax ax ax b
ax ax ax b
ax a x ax b
+ +⋅⋅⋅+ =
⎧
⎪
++⋅⋅⋅+=
⎪
⎨
⎪
⎪
++⋅⋅⋅+=
⎩
n
(1.66)
Эта система может рассматриваться как равенство двух одностолбцовых матриц:
11 1 12 2 1 1
21 1 22 2 2 2
11 2 2
..............................
nn
nn
nn nnn
ax ax ax b
ax ax ax b
ax a x ax b
++⋅⋅⋅+
++⋅⋅⋅+
=
n
⋅
⋅⋅
+ +⋅⋅⋅+
. (1.67)
Введем в рассмотрение три матрицы: матрицу
A
системы (1.66) – квадратную
матрицу порядка (размера )
n nn×
53

11 12 1
21 22 2
12
n
n
nn nn
aa a
aa a
A
aa a
⋅⋅⋅
⋅⋅⋅
=
⋅
⋅⋅ ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅
⋅⋅⋅
(1.68)
и две одностолбцовые матрицы: матрицу
X
из неизвестных и матрицу из сво-
B
бодных членов.
11
22
,
nn
.
x
b
x
b
XB
x
b
==
⋅
⋅⋅ ⋅⋅⋅
(1.69)
Тогда по правилу умножения матриц левая часть матричного равенства
(1.67) может быть представлена как произведение матриц
,
A
X
а правая часть -
матрица . Таким образом, матричное равенство (1.67), а, следовательно, и сис-
B
тема линейных уравнений (1.66) с неизвестными может быть записана в виде
n n
одного матричного уравнения
A
XB
=
. (1.70)
Матричное уравнение (1.70) равносильно системе (1.66) и содержит неиз-
вестную матрицу
X
. Решая это уравнение, то есть, определяя матрицу
X
, нахо-
дим сразу значения всех неизвестных
12
, ,..., .
n
x
xx
Допустим, что определитель матрицы А системы (1.66) отличен от нуля, в
этом случае по теореме Крамера система (1.66) совместна и имеет единственное
решение. Тогда, умножив обе части матричного уравнения (1.70) на
1
A
−
слева,
получим
11
,
A
AX A B
−−
=
откуда, учитывая, что
1
,
A
AE
−
=
а ,EX X
=
будем иметь
1
XAB
−
=
. (1.71)
Мы получили решение системы (1.66) в матричном виде. Соотношение
(1.71) эквивалентно формулам Крамера, что легко установить, если заменить об-
ратную матрицу ее выражением и произвести умножение матриц. Матричная за-
пись решения (1.71) компактна и красива, но не избавляет нас от вычислений, по-
скольку матрица
1
A
−
нам заранее не дана.
Случай произвольных систем линейных уравнений и решение систем ли-
нейных уравнений методом Гаусса рассмотрены в пособии [1].
54

Решение задач
Задача 1. Умножить матрицу
230
311
A
−
=
−
на матрицу
12 23
0112
1301
B
−−
=−
−
.
Решение. Так как матрица
A
имеет три столбца, а матрица - три строки,
B
то умножение матрицы
A
на матрицу возможно, при этом произведением мат-
B
рицы
A
на матрицу будет матрица , состоящая из двух строк и четырех
B
C
столбцов.
Вычислим элементы матрицы
C
11
12
13
14
21
22
23
24
(2)(1) 30 01 2,
(2)2 31 0(3) 1,
(2)(2) 3(1) 00 1,
(2)3 32 01 0,
3( 1) ( 1)0 1 1 2,
32 (1)1 1(3) 2,
3( 2) ( 1)( 1) 1 0 5,
33 (1)2 11 8.
c
c
c
c
c
c
c
c
=− − + ⋅ + ⋅=
=− + ⋅+ − =−
=− − + − + ⋅ =
=− + ⋅ + ⋅=
=−+− +⋅=−
=⋅+− +− =
=−+−−+⋅=−
=⋅+− +⋅=
Таким образом,
2110
.
2258
AB
−
⋅=
−−
Заметим, что в данном примере может идти речь только о произведении
A
B
матрицы
A
на матрицу . Произведение матрицы на матрицу
B B
A
не имеет
смысла, так как число столбцов матрицы не равно числу строк матрицы
B
A
.
Задача 2. Вычислить произведения
A
B
и , если
BA
21
01
A
−
=
и
13
.
12
B =
−
Решение.
A
B⋅=
2113 2162 34
01 12 0102 12
−+−
==
−−+−
,
132 1 20 13 22
.
12 0 1 20 12 23
BA
−+−+
⋅= = =
−−++−
55
Итак, в данном примере оба произведения
A
B
и имеют смысл, но
BA
A
.BBA≠
Задача 3. Найти обратную матрицу для матрицы
12 1
21 2
10 1
A
=
−
−
.
Решение. Вычислим определитель матрицы А
11
12 1 1 0 0
34
( ) 2 1 2 2 3 4 1( 1) 2.
22
10 1 1 2 2
DA
+
−−
=−=−−=−
−−
=
Определитель матрицы отличен от нуля, следовательно, матрица неособенная и
имеет обратную матрицу
1
A
−
, вычисляемую по формуле (1.65). Составим алгеб-
раические дополнения элементов матрицы
A
:
11
11
12
12
13
13
21
21
22
22
12
(1) 1 0 1;
01
22
(1) (2 2) 0;
11
21
(1) 0 1 1;
10
21
(1) (2 0) 2;
01
11
(1) 1 1 2;
11
A
A
A
A
A
+
+
+
+
+
−
=− = − =
−
=− =− − =
−
=− = + =
−
=− =− − =−
=− = + =
−
23
23
31
31
32
32
33
33
12
(1) (0 2) 2;
10
21
(1) 4 1 5;
12
11
(1) (2 2) 4;
22
12
(1) 1 4 3;
21
A
A
A
A
+
+
+
+
=− =− + =−
−
=− =−− =−
−
=− =−−− =
−
=− = − =−
56
По формуле (1.65) найдем обратную матрицу
15
1
125
22
1
1
024 01 2
2
123 1 3
1
22
A
−
−
−−
−
==
−−
−
−
.
Проверим правильность результата, используя определение обратной мат-
рицы (1.63). Для этого перемножим матрицы
A
и
1
:A
−
1
15
1
12 1
22
21 2 0 1 2
10 1 1 3
1
22
11 53
01214
100
22 22
101 212 523 010 .
11 53001
01010
22 22
AA
E
−
−−
⋅= −⋅ =
−
−−
++ −+− −+−
=+−−++−++= =
−++ +− +−
Таким образом, матрица
1
A
−
вычислена верно.
Задача 4. Даны матрицы
,,
A
BC
. Найти матрицу
1
2PBC A
−
=−
23
13 2 2 3
,10,
02 1 1 2
21
BCA
−− −
===.
−
−−
Решение. Найдем произведение матриц и
C
B
.BC K
=
Это произведение определено, так как число столбцов матрицы совпа-
B
дает с числом строк матрицы . Матрица
C KBC
=
должна иметь две строки и два
столбца, то есть должна быть квадратной матрицей второго порядка. Найдем ее
элементы по правилу умножения матриц (1.55):
11
12
21
22
(1)2 31 (2)(2) 5,
(1)3 30 (2)(1) 1,
02 21 1(2) 0,
03 20 1(1) 1.
k
k
k
k
=− ⋅ + ⋅+− − =
=
−⋅+⋅+− −=−
=⋅+⋅+− =
=⋅+⋅+− =−
Таким образом,
57
51
01
BC K
−
==
−
.
Найдем определитель матрицы
A
23
() 4 (3) 1.
12
DA
−
=
=− − − =−
−
Так как определитель матрицы
A
отличен от нуля, то обратная матрица
1
A
−
су-
ществует и может быть вычислена по формуле (1.65):
11 21
1
12 22
1
,
()
AA
A
AA
DA
−
=
где
11 12
11 21
12 22
12 22
(1) (2) 2, (1) (3) 3,
(1) 1 1, (1) 2 2.
AA
AA
++
++
=
−−=− =− −=
=− ⋅=− =− ⋅ =
Таким образом,
1
23
(1) .
12
A
−
−
=−
−
Окончательно получим
1
51 23 15
22
01 12 23
PBC A
−
−−
=− = + =
−− −
.
Задача 5. Решить систему уравнений
123
12 3
12 3
7231
93 41
53
xxx
xx x
xx x
++=
⎧
⎪
++=
⎨
⎪
++ =
⎩
3,
5,
14
с помощью обратной матрицы.
Решение. Запишем данную систему в виде одного матричного уравнения
A
,XB=
где
723
934,
513
A =
1
2
3
13
,1
14
x
Xx B
x
==5.
Для решения матричного уравнения с помощью обратной матрицы вычислим оп-
ределитель матрицы
A
723
() 9 3 4 3.
513
DA
=
=
58
Так как , то матрица
() 0DA≠
A
имеет обратную
1
A
−
, для вычисления которой
найдем алгебраические дополнения элементов матрицы
A
:
11
11
12
12
13
13
21
21
22
22
23
23
31
31
32
32
34
(1) 9 4 5;
13
94
( 1) (27 20) 7;
53
93
(1) 9 15 6;
51
23
(1) (6 3) 3;
13
73
(1) 21 15 6;
53
72
( 1) (7 10) 3;
51
23
(1) 8 9 1;
34
73
( 1) (28 27) 1
94
A
A
A
A
A
A
A
A
+
+
+
+
+
+
+
+
=− = − =
=− =− − =−
=− = − =−
=− =− − =−
=− = − =
=− =− − =
=− = − =−
=− =− − =−
33
33
;
72
(1) 21 18 3;
93
A
+
=− = − =
Тогда
1
531
1
761
3
633
A
−
.
−
−
=
−−
−
Найдем решения системы по формуле (1.71):
1
53113 6 2
11
76115 15 5
33
63314 9 3
XAB
−
−−
==− −⋅=−=−
−
.
Таким образом, мы нашли решение данной системы:
12 3
2; 5; 3.xx x
=
=− =
Вопросы для самопроверки по теме 1.3
1. Какая матрица называется единичной? Как она обозначается?
59
