Судавная О.И., Фролов С.В Типовые расчеты по высшей математике. Методические указания и задачи для студентов вечернего отделения. I семестр
Подождите немного. Документ загружается.

О.И. Судавная, С.В. Фролов
Типовые расчеты
по высшей математике
Методические указания и задачи
для студентов вечернего отделения
I семестр
Санкт-Петербург
2009

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ
О.И. Судавная, С.В. Фролов
ТИПОВЫЕ РАСЧЕТЫ ПО ВЫСШЕЙ
МАТЕМАТИКЕ
Методические указания и задачи для
студентов вечернего отделения
I семестр
Методическое пособие
Санкт-Петербург
2009

О.И. Судавная, С.В. Фролов Типовые расчеты по высшей математике.
Методические указания и задачи для студентов вечернего отделения. I
семестр. – СПб: СПбГУ ИТМО, 2009. – 46 с.
Пособие содержит типовые расчеты с методическими указаниями по
темам
• линейная алгебра
• векторная алгебра
• аналитическая геометрия
• пределы
• производные
• исследование функций
Пособие адресовано студентам первого курса вечернего отделения СПбГУ
ИТМО
Рекомендовано к печати Ученым Советом естественнонаучного факультета
СПбГУ ИТМО 29 сентября 2009 года, протокол № 2.
В 2007 году СПбГУ ИТМО стал победителем конкурса инновационных
образовательных программ вузов России на 2007–2008 годы. Реализация
инновационной образовательной программы «Инновационная система
подготовки специалистов нового поколения в области информационных и
оптических технологий» позволит выйти на качественно новый уровень
подготовки выпускников и удовлетворить возрастающий спрос на
специалистов в информационной, оптической и других
высокотехнологичных отраслях экономики.
©Санкт-Петербургский государственный университет информационных
технологий, механики и оптики, 2009
© О.И. Судавная, С.В. Фролов 2009
Введение
Типовые расчеты по математике для студентов первого курса
вечернего отделения в первом семестре содержат 2 типовых расчета
по темам
•
«Линейная и векторная алгебра. Аналитическая
геометрия»
•
«Введение в математический анализ»
Каждый из типовых расчетов включает 26 вариантов по пяти
р
азличным разделам. Перед заданиями помещены методические
указания, основные теоретические формулы и разобранные решения
наиболее типичных задач.
Рекомендуемые пособия:
1. Брылевская Л.И., Лапин И.А., Ратафьева Л.С.
Аналитическая геометрия и линейная алгебра. Учебное
пособие. СПб: СПбГУ ИТМО, 2008.
2. Лапин И.А., Ратафьева Л.С., Фролов В.М. Математический
анализ I. Учебное пособие. СПб: СПбГУ ИТМО, 2008.
Типовой расчет по теме «Линейная и векторная алгебра.
Аналитическая геометрия»
Методические указания
Содержание расчетных заданий
I. Исследование системы линейных уравнений методом
Гаусса.
II. 1) Составление системы линейных уравнений.
2) Решение системы методом Крамера.
3) Решение системы матричным методом.
III. Уравнения прямой и плоскости в пространстве.
IV. Уравнения кривых второго порядка на плоскости и
поверхностей второго порядка в пространстве.
.
3
Образцы решения задач по теме «Системы линейных уравнений»
Пример 1. С помощью метода Гаусса найдите решения системы
14
1234
1234
1234
2
9
2
3
2
0
2322
12
xx
xx xx
xxxx
xx x x
−
=
⎧
⎪
−++
=
⎪
⎨
+−+
=
⎪
⎪
−+−
=
⎩
, или докажите ее несовместность.
Решение. Преобразуем расширенную матрицу системы:
100 29 100 2 9
2 111 3 0 115 15
12 11 0 02 13 9
232212 0322 6
A
−−
⎛⎞⎛
⎜⎟⎜
−−
⎜⎟⎜
=→
⎜⎟⎜
−−
⎜⎟⎜
−− − −
⎝⎠⎝
⎞
⎟
−
⎟
→
⎟
−
⎟
⎠
⎞
⎟
−
⎟
⎟
⎟
⎠
5
R
4
100 2 9 100 2 9
0 1 1 5 15 0 1 1 5 15
0 0 1 13 39 0 0 1 13 39
00 1 1339 0000 0
−−
⎛⎞⎛
⎜⎟⎜
−− −
⎜⎟⎜
→→
⎜⎟⎜
−−
⎜⎟⎜
−−
⎝⎠⎝
.
На первом шаге ко второй строке прибавлена первая строка, умноженная
на (– 2), к третьей строке прибавлена первая строка, умноженная на (– 1), к
четвертой строке прибавлена первая строка, умноженная на (– 2). На втором
шаге к третьей строке прибавлена вторая строка, умноженная на 2, к
четвертой строке прибавлена вторая строка, умноженная на (– 3). На
третьем шаге к четвертой строке прибавлена третья строка.
Восстановим систему:
14
23 4
34
29
51
13 39
xx
xx x
xx
−=
⎧
⎪
−++ =−
⎨
⎪
+=−
⎩
.
Придадим переменной x
4
произвольное значение . Тогда
, ,
4
,xcc=∈
3
13 39xc=− −
2
82xc=− −
1
29xc
=
+
. Таким образом получили
бесконечное множество решений системы, зависящее от произвольного
параметра c:
1
2
3
4
29
824
13 39
x
c
x
c
x
c
x
c
=+
⎧
⎪
=− −
⎪
⎨
=− −
⎪
⎪
=
⎩
,
c
.
R∈
4

Матричная форма записи полученного множества решений имеет вид:
29
824
⎞
⎟
⎟
⎟
⎟
⎠
13 39
10
Xc
⎛⎞⎛
⎜⎟⎜
−−
⎜⎟⎜
=+
⎜⎟⎜
−−
⎜⎟⎜
⎝⎠⎝
R
,
c
∈
.
Матрица, стоящая в первом слагаемом, представляет собой общее
решение однородной системы, соответствующей исходной, а матрица во
втором слагаемом – частное решение исходной неоднородной системы.
Ответ: ,
29
824
⎞
⎟
⎟
⎟
⎟
⎠
13 39
10
Xc
⎛⎞⎛
⎜⎟⎜
−−
⎜⎟⎜
=+
⎜⎟⎜
−−
⎜⎟⎜
⎝⎠⎝
cR
∈
.
Пример 2. . С помощью метода Гаусса найдите решения системы
, или докажите ее несовместность.
123
123
12 3
54
23
43
xx x
xxx
xx x
+−=−
⎧
⎪
−+=
⎨
⎪
+− =−
⎩
5
2
4
Решение.
15 45 1 5 45 1 5 4 5
2312 013912 013 9 12
4 1 3 4 0 19 13 16 0 0 2 13 20 13
A
−− −− − −
⎛⎞⎛ ⎞⎛
⎜⎟⎜ ⎟⎜
=− →− →−
⎜⎟⎜ ⎟⎜
⎜⎟⎜ ⎟⎜
−− − − −
⎝⎠⎝ ⎠⎝
⎞
⎟
⎟
⎟
⎠
.
На первом шаге из второй строки вычтена ее первая строка, умноженная
на 2, а из третьей строки вычтена первая строка, умноженная на 4. На втором
шаге к третьей строке прибавлена вторая строка, умноженная на – 19/13.
Восстановим систему:
12 3
23
3
54
13 9 12
22
13 13
xx x
xx
x
+−=−
⎧
⎪
−+=
⎨
⎪
⎩
5
0
−
=−
.
Из последнего уравнения следует, что x
3
= 10, тогда из второго
уравнения получим –13x
2
= – 78, откуда x
2
= 6. Найдем x
1
из первого
уравнения: x
1
= – 5 + 40 – 30 = 5. В результате получим
. Ответ:
1
2
3
55
6
10 10
x
xX
x
=
⎧⎛
⎪
⎜
=⇒ =
⎨
⎜
⎪⎜
=
⎩⎝
6
⎞
⎟
⎟
⎟
⎠
5
6
10
X
⎛⎞
⎜⎟
=
⎜⎟
⎜⎟
⎝⎠
5

Пример 3. С помощью метода Гаусса найдите решения системы
, или докажите ее несовместность.
123
123
12 3
234
2
33 2 1
xxx
xxx
xx x
++=
⎧
⎪
+−=
⎨
⎪
++=
⎩
3
0
⎞
⎟
⎟
⎟
⎠
3
Решение. Преобразуем расширенную матрицу системы:
.
1234 12 34 12 34
2113 0375 0375
3321003720003
A
⎛⎞⎛ ⎞⎛
⎜⎟⎜ ⎟⎜
= − →−−−→−−−
⎜⎟⎜ ⎟⎜
⎜⎟⎜ ⎟⎜
−−−
⎝⎠⎝ ⎠⎝
На первом шаге из второй строки вычтена первая строка, умноженная на
2, а из третьей строки вычтена первая строка, умноженная на 3. На втором
шаге из третьей строки вычтена вторая строка.
Восстановив по третьей строке матрицы третье уравнение, получим
, откуда следует, что уравнение, а значит, и система несовместны.
3
0x⋅=
Ответ: система несовместна.
Образцы решения задач по теме «Векторная алгебра»
Пример 4. Вектор
{
}
,,dxyz=
удовлетворяет следующим условиям:
а) скалярное произведение вектора
d
на вектор
{
}
2,3, 4a
=
−
равно – 4,
б) проекция вектора на вектор
d
{
}
1, 2, 2b
=
−
равна – 1,
в) вектор
d
ортогонален вектору
{
}
1, 1, 0c
=
−
.
1) Составьте систему линейных уравнений, связывающих координаты x,
y, z вектора
d
.
2) Найдите координаты x, y, z вектора
d
двумя способами: по теореме
Крамера и с помощью обратной матрицы.
3) На векторах
,,abc
построена треугольная пирамида. Найдите ее
высоту, опущенную на грань, проходящую через векторы
иab
.
Решение. 1) Запишем условия, которым удовлетворяет вектор
d
,
в
координатной форме:
а) ;
4234da x y z⋅=−⇒+−=−
4
б)
22
112
3
b
xyz
пр dx
+−
=− ⇒ =− ⇒ + − =−
23yz
;
в) .
00dc dc xy⊥⇒⋅=⇒−=
Получили систему трех уравнений с тремя неизвестными:
6
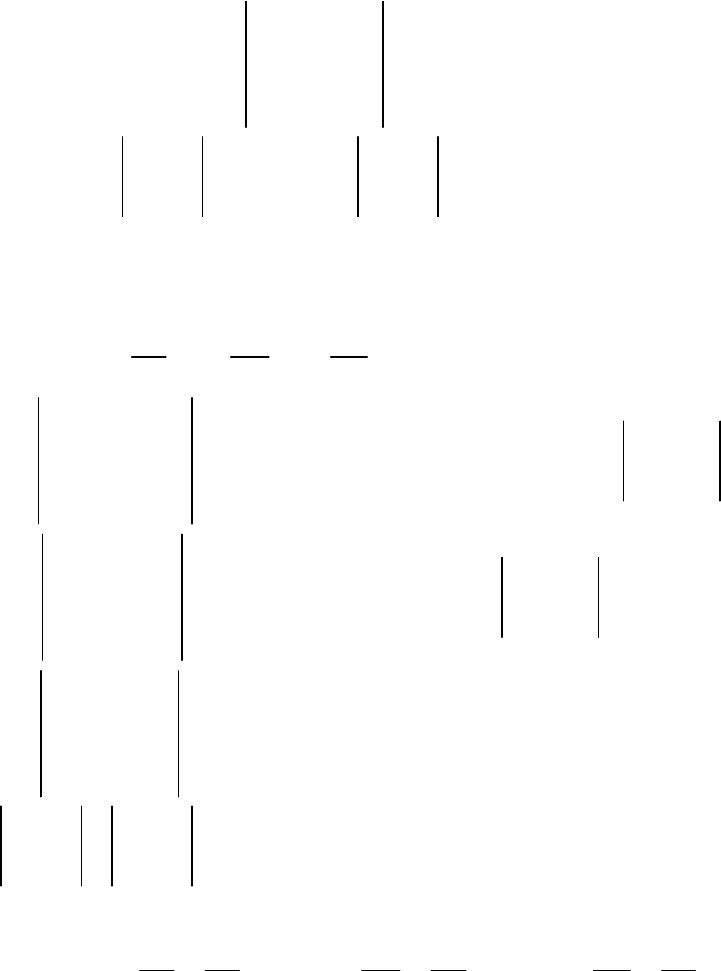
234
22
0
xyz
xyz
xy
4
3
+
−=−
⎧
⎪
+
−=
⎨
⎪
−
−
=
⎩
.
2) Решим систему с помощью теоремы Крамера. Для этого найдем
определитель матрицы
23 4
12 2
110
A
−
⎛⎞
⎜⎟
=
⎜⎟
⎜⎟
−
⎝⎠
−
системы:
31 32 33
23 4
12 21 1 0
110
DAA
−
=−=⋅−⋅+⋅
−
A=
31 32
34 24
1( 1) 1( 1)
22 12
++
−
−
=⋅− ⋅ −⋅− ⋅ =
−−
(– 6 + 8) + (– 4 + 4) = 2.
При вычислении определителя была применена теорема разложения по
элементам третьей строки.
Таким образом,
20
D
=≠
, следовательно, система имеет единственное
решение
3
12
,,
D
DD
xyz
DD
===
D
. Найдем определители D
1
, D
2
, D
3
.
1313233
A
43 4
32 20 1 0
010
DAA
−−
=− − = ⋅ − ⋅ + ⋅ =
−
5
44
1( 1) 8 12 4
32
−
−
−
⋅− = − =−
−−
2313233
244
44
1321 0 0 812
32
10 0
DAAA
−−
−−
=−−=⋅+⋅+⋅= =−=−
−−
4
3313233
23 4
12 31 1 0
110
DAAA
−
=−=⋅−⋅+⋅=
−
3424
(9 8) (6 4) 3
2313
−−
=+=−++−+=−
−−
Координаты вектора
d
равны
1
4
2
2
D
x
D
−
===−
,
2
4
2
2
D
y
D
−
=
==−
,
3
3
1, 5
2
D
z
D
−
=
==−
.
Решим ту же систему с помощью обратной матрицы. Для этого
запишем систему в матричной форме: AX = B, где А – матрица системы, X –
столбец, составленный из неизвестных, B – столбец, составленный из
свободных членов. Умножив матричное уравнение слева на матрицу А
–1
,
7
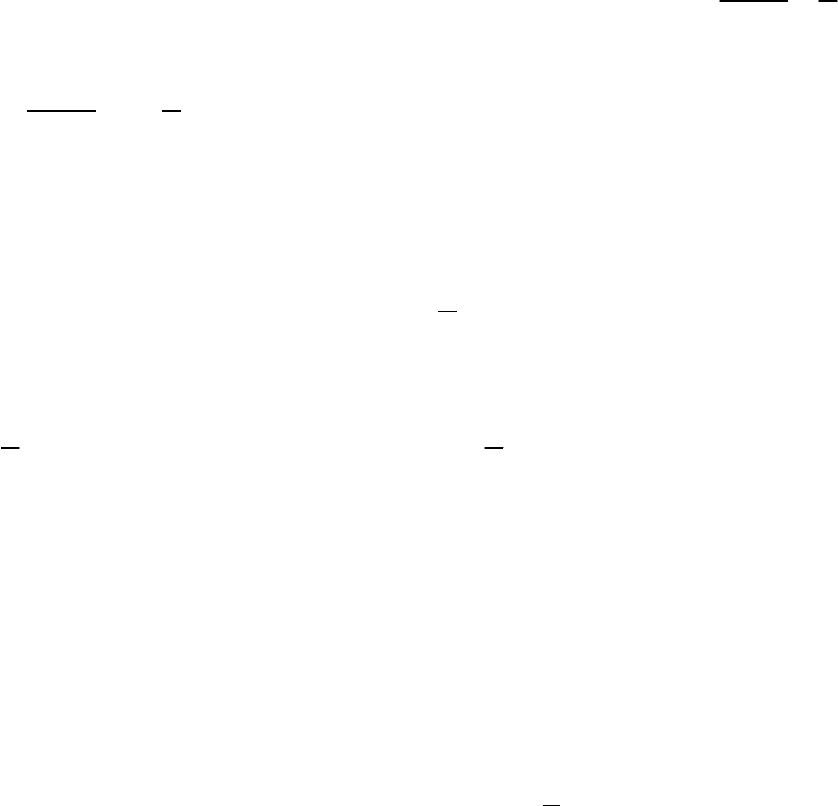
получим матричную форму решения системы X = А
–1
B. Поскольку
определитель матрицы А отличен от нуля (
20
D
=
≠
), обратная матрица А
–1
существует.
Найдем алгебраические дополнения элементов матрицы системы:
11 12 13
21 22 23
31 32 33
2; 2; 3;
4; 4; 5;
2; 0; 1.
AAA
AAA
AAA
=
−=−=−
=
==
=
==
Составим из них матрицу
223
445
201
B
−
−−
⎛⎞
⎜
=
⎜
⎜⎟
⎝⎠
⎟
⎟
. Транспонируем полученную
матрицу: .
242
240
351
T
CB
−
⎛⎞
⎜⎟
==−
⎜⎟
⎜⎟
−
⎝⎠
Для получения обратной матрицы, умножим матрицу С на число
11
() 2DA
=
:
1
242 1 2 1
11
240 1 2 0
() 2
3 5 1 1,5 2,5 0,5
AC
DA
−
−−
⎛⎞⎛
⎜⎟⎜
=⋅=⋅− =−
⎜⎟⎜
⎜⎟⎜
−−
⎝⎠⎝
⎞
⎟
⎟
⎟
⎠
.
Проверка подтверждает правильность вычислений:
1
23 4
12 2
110
AA
−
−
⎛⎞
⎜⎟
⋅= −⋅
⎜⎟
⎜⎟
−
⎝⎠
242
1
240
2
351
−
⎛⎞
⎜⎟
⋅
−=
⎜⎟
⎜⎟
−
⎝⎠
4612 0 0 200 100
11
048100 02001
22
0 0 200 002 001
−− +
⎛⎞⎛
⎜⎟⎜
=⋅ +− =⋅ =
⎜⎟⎜
⎜⎟⎜
++
⎝⎠⎝
0
⎞⎛⎞
⎟⎜⎟
⎟⎜⎟
⎟⎜⎟
⎠⎝⎠
−
⎛⎞
⎜⎟
−
⎜⎟
⎜⎟
−
⎝⎠
.
Найдем теперь столбец X:
X = А
–1
B = .
121 4 46 2
120 3 46 2
1,5 2,5 0,5 0 6 7,5 1,5
−−−
⎛⎞⎛⎞⎛⎞
⎜⎟⎜⎟⎜⎟
−⋅−=−=
⎜⎟⎜⎟⎜⎟
⎜⎟⎜⎟⎜⎟
−−
⎝⎠⎝⎠⎝⎠
Таким образом, x = – 2, y = – 2, z = – 1,5. Вектор
d
равен
{
}
2, 2, 1,5d =− − −
.
3) Для нахождения высоты h треугольной пирамиды, построенной на
векторах
,,abc
, воспользуемся формулой
1
3
VhS=
, где V – объем, S –
8
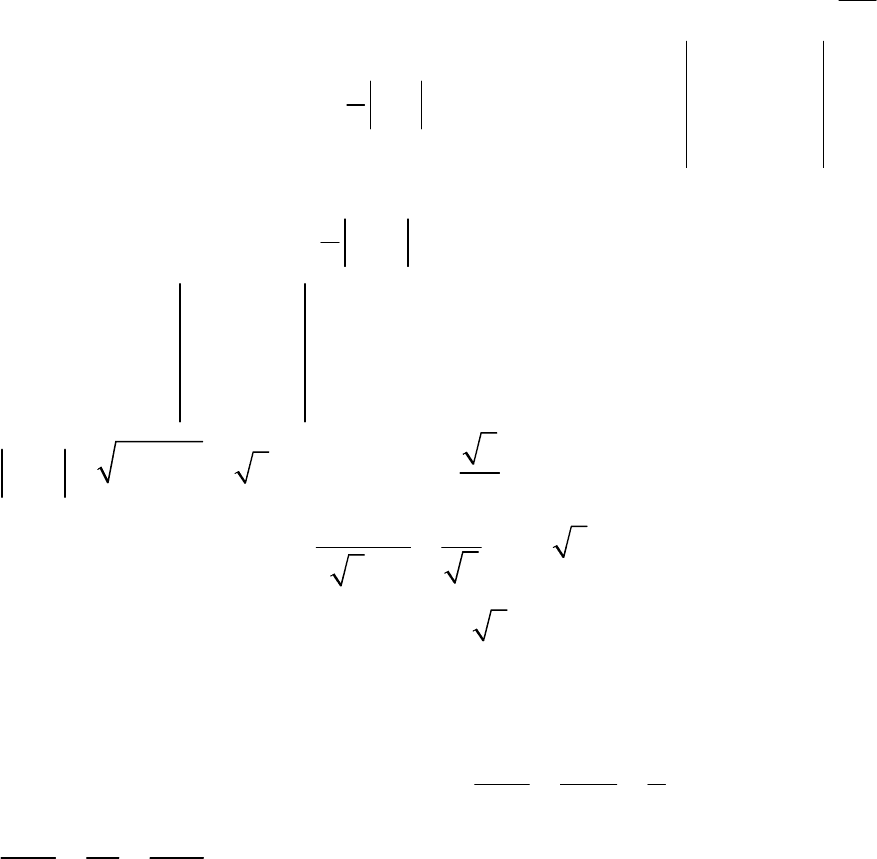
площадь основания пирамиды. Из этой формулы следует, что
3V
h
S
=
(*).
Объем пирамиды равен
1
6
Vabc
. Поскольку
23 4
12 22
110
abc
−
=
−=
, то
−
=
V = 1/3. Площадь основания, т. е. площадь треугольника, построенного на
векторах , равна
иab
1
2
Sa=×b
. Найдем векторное произведение векторов
:
иab
23 4 2
12 2
ijk
ab i k×= −= +
−
. Модуль векторного произведения равен
22
21ab×= + =
5, значит,
5
2
S =
. Подставив найденные числа в
формулу (*), получим
()
3(1/3) 2
0, 4 5
5
5/2
h
⋅
===.
Ответ:
{
}
2, 2, 1,5d =−−−
, 0, 4 5h = .
Образцы решения задач по теме «Аналитическая геометрия»
Пример 5. Докажите, что прямые
11
213
x
yz
−
−
=
=
(1) и
11
113
x
yz−−
==
−
(2) пересекаются и напишите уравнение плоскости,
проходящей через эти прямые.
Решение. 1) Прямая (1) проходит через точку А
1
(1;1;0) параллельно
направляющему вектору
1
{2;1;3}s
=
. Прямая (2) проходит через точку
А
2
(1;0;1) параллельно направляющему вектору
2
{1; 1; 3}s
=
−
. Вычислим
координаты вектора
12
A
A
→
, соединяющего точки А
1
и А
2
:
12
{1 1;0 1;1 0} {0; 1;1}AA
→
=− − − = − .
Найдем смешанное произведение векторов
1
s
,
2
s
и
12
A
A
→
:
9
